



Artigos
Educação Matemática crítica e uso de tecnologias: cenários para investigação com o jogo da corrida dos cavalos
Critical Mathematical education and use of technologies: scenarios for investigation with the horse racing game
Educación Matemática crítica y uso de tecnologías: escenarios de investigación con el juego de carreras de caballos
Revista de Ensino de Ciências e Matemática
Universidade Cruzeiro do Sul, Brasil
ISSN-e: 2179-426X
Periodicidade: Trimestral
vol. 12, núm. 3, 2021
Recepção: 03 Fevereiro 2021
Aprovação: 17 Março 2021
Publicado: 23 Maio 2021

Resumo: Neste trabalho são expostos os resultados de uma investigação qualitativa, em andamento, cujo objetivo é apresentar e explorar as possibilidades educacionais no que concerne à ocorrência de cenários para investigação, que possam ocasionar a Educação Matemática Crítica, por meio do “Jogo da Corrida dos Cavalos”. O jogo é baseado nas concepções de Skovsmose (2000, 2001, 2006, 2008) e é relacionado aos eixos temáticos de Probabilidade e Estatística, como propõe a Base Nacional Comum Curricular (BNCC). A exploração e a apresentação das questões envolvidas nos cenários são feitas de forma investigativa, analisando as diversas estratégias de resolução, contrapondo-se ao paradigma do exercício e ao ensino tradicional. Além disso, na exploração dos possíveis cenários, os recursos tecnológicos, em especial o computador, tiveram um papel de destaque, visto que foi implementada uma simulação que auxiliou nas questões de tratamento analítico mais complexo. Sob a perspectiva das abordagens investigativas, assim como dos pressupostos teóricos da Educação Matemática Crítica, conseguimos constatar as potencialidades dos cenários para investigação e dos recursos tecnológicos para uma possível ação pedagógica em sala de aula.
Palavras-chave: Probabilidade, Cenários para Investigação, Educação Matemática Crítica, Recursos Computacionais.
Abstract: scenarios for investigation with the horse racing game : In this work, the results of an ongoing qualitative investigation are exposed, whose objective is to present and explore the educational possibilities for the occurrence of scenarios for investigation, through the “Horse Racing Game”, which can cause Critical Mathematical Education. The game is based on the conceptions of Skovsmose (2000, 2001, 2006, 2008) and is related to the thematic axes of Probability and Statistics, as proposed by the National Common Curricular Base (BNCC). The exploration and presentation of the issues involved in the scenarios are done in an investigative way, analyzing different strategies of resolution, opposing the exercise paradigm and traditional teaching. In addition, in the exploration of possible scenarios, technological resources, especially the computer, played a prominent role, since a simulation was implemented, which helped with issues that have a more complex analytical treatment. From the perspective of investigative approaches, as well as the theoretical assumptions of Critical Mathematical Education, we were able to verify the potential of the scenarios for investigation and the technological resources for a possible pedagogical action in the classroom. Keywords: Probability. Landscapes of Investigation. Critical Mathematical Education. Computational Resources. Educación Matemática crítica y uso de tecnologías: escenarios de investigación con el juego de carreras de caballos
Resumen: Este trabajo expone los resultados de un análisis cualitativo en curso, cuyo objetivo es presentar y explorar las posibilidades educacionales con respeto a ocurrencia de escenarios investigativos, que pueden resultar en Educación Matemática Crítica a través del “Juego de Carrera de Caballos”. El juego se basa en los conceptos de Skovsmose (2000, 2001, 2006, 2008) y se relaciona los ejes temáticos de Probabilidad y Estadística, según la Base Nacional Común Curricular (BNCC). La exploración y la presentación de las cuestiones envueltas en los escenarios se realizan de manera investigativa, de suerte que se analiza las diversas estratégicas de resolución, y contrapóndosela al paradigma del ejercicio y a la enseñanza tradicional. Además, en el rastreo de los posibles escenarios, los recursos tecnológicos, en especial el computador, fueron preponderantes, una vez que se implementó una situación que favoreció en las cuestiones de tratamiento analítico más complejo. Bajo las perspectivas de los enfoques investigativos, tal como los presupuestos teóricos de la Educación Matemática Crítica, conseguimos comprobar el potencial de los escenarios de investigación y de los recursos tecnológicos de una posible acción pedagógica en clase de aula.
Palabras clave: Probabilidad, Escenario de Investigación, Educación Matemática Crítica, Recursos Computacionales.
1. Introdução
O presente artigo propõe-se a apresentar e explorar possíveis cenários para investigação no jogo pedagógico chamado de “Jogo da Corrida de Cavalos”, sugerido pelos autores que se baseiam nas ideias de Skovsmose (2000), alvitrando novas possibilidades educacionais a fim de exercer a Educação Matemática Crítica. A motivação para o estudo desse jogo originou-se de uma experiência anterior dos autores, em que obtiveram resultados pedagógicos positivos após sua aplicação em turmas do ensino básico.
Segundo Skovsmose (2000), um cenário para investigação é um ambiente que pode dar suporte a um trabalho de investigação. Contrapondo-se ao paradigma do exercício, em que os alunos permanecem condicionados a sua resolução, nos cenários para investigação, eles são convidados a se envolverem em um processo de exploração do problema em questão, fazendo com que assumam uma postura mais ativa em seu processo de aprendizagem.
Logo, as abordagens investigativas estão estritamente relacionadas à corrente educacional denominada Educação Matemática Crítica. Segundo Teres (2014), dentre as características dessa corrente, está a preocupação com o desenvolvimento de competências que tornem o aluno capaz de interpretar e agir numa situação social e política estruturada pela Matemática.
Sobre a abordagem investigativa realizada neste trabalho, faremos uso intenso do computador no auxílio à investigação das questões que serão verificadas, porque a utilização de recursos computacionais permite novos caminhos na busca por soluções. Borba e Villareal (2005) destacam a investigação com computador como uma situação em que existe: “...a possibilidade de testar uma conjectura usando um grande número de exemplos e a chance de repetir os experimentos, devido ao rápido feedback dado pelos computadores”. Além disso, a investigação com meios tecnológicos permite o desenvolvimento do pensamento computacional, habilidade que vem ganhando importância na Educação Matemática. Nesse sentido, a Base Nacional Comum Curricular (BNCC) determina que:
os estudantes devem utilizar conceitos, procedimentos e estratégias não apenas para resolver problemas, mas também para formulá-los, descrever dados, selecionar modelos matemáticos e desenvolver o pensamento computacional, por meio da utilização de diferentes recursos da área. (BRASIL, 2018, p. 470).
Dessa forma, entendemos que o jogo chamado de “Jogo da Corrida dos Cavalos” pode ser utilizado como ferramenta para verificar as potencialidades do uso de recursos tecnológicos no contexto das abordagens investigativas. Machado et. al (2020) aplicaram o jogo, em formato de tabuleiro físico, em sala de aula e verificaram seu potencial pedagógico na aprendizagem dos eixos temáticos de Probabilidade e Estatística de alunos do ensino médio. No presente artigo, implementamos uma simulação computacional do jogo para auxiliar no tratamento de novos possíveis cenários para investigação em sala de aula a fim de conduzir a uma Educação Matemática Crítica. Nessa perspectiva, os cenários tentam responder a seguinte questão norteadora: Como o “Jogo da Corrida dos Cavalos” e os recursos tecnológicos podem ser utilizados para provocar Educação Matemática Crítica através de abordagens investigativas para o ensino de Probabilidade e Estatística?
Portanto, o objetivo desse trabalho é apresentar e explorar as possibilidades educacionais para a ocorrência de cenários para investigação, que possam ocasionar a Educação Matemática Crítica, por meio do “Jogo da Corrida dos Cavalos”. Ao propor cenários para investigação detalhados, oferecemos suporte ao professor que deseje utilizar o “Jogo da Corrida dos Cavalos” como convite para uma abordagem investigativa em suas aulas[1]. No blog, o docente que desejar aplicá-lo em sala de aula poderá encontrar uma versão digital animada, bem como a simulação computacional mencionada, a qual permite fazer com que o computador execute um número muito grande de partidas e exiba as estatísticas associadas aos resultados do jogo.
No que concerne à divisão do artigo, essa se faz através da seguinte organização: na seção Educação Matemática Crítica, Cenários para Investigação e Tecnologias, são apresentados os principais conceitos relacionados às abordagens investigativas, bem como é realizada uma breve discussão sobre o uso de tecnologia em sala de aula; em Aspectos Metodológicos, apresentamos a metodologia de abordagens investigativas proposta por Alrø e Skovsmose (2006) e as informações da confecção do jogo; em Discussão sobre as possibilidades educacionais do jogo, apresentamos e exploramos possíveis cenários com o computador tendo um lugar de destaque na condução das investigações, bem como das análises e, nas Considerações Finais, sintetizamos as reflexões sobre o trabalho realizado, além de apresentar propostas para trabalhos futuros.
2. Educação Matemática Crítica, Cenários para Investigação e Tecnologias
2.1. Cenários para Investigação e a Educação Matemática Crítica
Para Skovsmose (2000), um cenário para investigação é um ambiente de aprendizagem que vem a contribuir para o desenvolvimento de um trabalho de investigação, de modo a levar os participantes a conjecturar, questionar, investigar e refletir com ações que os conduzam, durante todo o processo de aprendizagem, a uma autonomia crítica.
O conceito de cenários para investigação está relacionado com as ideias da Educação Matemática Crítica, a qual fundamenta-se em ideias da teoria Social-Histórico e Crítica da Educação, pressupondo relações estabelecidas entre a sociedade, a tecnologia e o progresso. A Educação Matemática assume sua dimensão crítica quando promove a autonomia no conjecturar, no pensar e no agir dos sujeitos envolvidos no processo educacional, sendo capaz de conduzi-los a ações de enfrentamento de conflitos e crises da sociedade, tornando-os cidadãos conscientes em seus papéis social, cultural e político (Skovsmose, 2001).
Para o desenvolvimento investigativo numa perspectiva crítica, Skovsmose (2000) sugere refletir sobre os dois paradigmas que permeiam as práticas de sala de aula: a prática investigativa, no contexto da Educação Matemática Crítica, em oposição às ideias da Educação Matemática Tradicional, centrada na atividade de exercícios.
Mover-se do paradigma do exercício em direção ao cenário para investigação pode contribuir para o enfraquecimento da autoridade da sala de aula tradicional de matemática e engajar os alunos ativamente em seus processos de aprendizagem. (Skovsmose, p. 66, 2000).
Skovsmose identificou seis (6) modelos que são obtidos com a combinação das referências: matemática pura, semi-realidade e realidade associadas com os paradigmas das práticas das salas de aula: exercícios ou cenários de investigação. A Tabela 1, a seguir, mostra um resumo dessas seis (6) possibilidades.
| Exercícios | Cenários de investigação | ||
| Referências | Matemática Pura | Exercícios apresentados no contexto da matemática pura. | Investigações numéricas realizadas com papel e lápis ou computador. |
| Semi-realidade | Situações artificiais. O único objetivo é chegar à solução única. | Problemas artificiais, mas que permitem explorações e justificativas. Podem gerar outras questões e estratégias de solução. | |
| Realidade | Exercícios | Atividades de investigação que podem usar recursos tecnológicos e materiais manipulativos. Os problemas são relacionados ao cotidiano dos alunos e formulados com a participação deles. | |
Sabemos que não é uma tarefa fácil motivar os alunos a participarem, ativamente, em seus processos de aprendizagem. Um determinado cenário pode ser um grande atrativo para um grupo de alunos, mas para outro não ser nada convidativo e interessante. Portanto, se um certo cenário será investigativo ou não, isso será evidenciado através da prática dos alunos e professores envolvidos.
O engajamento dos alunos a um cenário de investigação é proveniente, fundamentalmente, da aceitação. A aceitação do convite à investigação, segundo Skovsmose (2008), depende de fatores, como prioridade dos estudantes no momento do convite, natureza da investigação e modo como o convite é feito. Nesse sentido, segundo Freire (1970), “os conteúdos e metodologias em uma educação crítica precisam ser desenvolvidos, com os estudantes, na busca de ideias e de experiências que deem significados as suas vidas”.
Sob os pressupostos acima, localizamos nossas propostas de investigação levantando convites e possibilidades de explorações para sala de aula em atividades que promovam reflexão e autonomia crítica no pensar, inclusive, no que concerne à emancipação dos alunos quanto ao uso de recursos tecnológicos. Considerando a importância que tais recursos assumirão ao longo do presente artigo, apresentaremos uma breve discussão sobre o uso de tecnologias no ensino de Matemática.
2.2 Os Recursos Tecnológicos no Ensino de Matemática
No Brasil, encontram-se pesquisas de educadores matemáticos como D´Ambrósio (1999), que associam a introdução das novas tecnologias no ensino à possibilidade de quebra do paradigma vigente à época – o ensino tradicional, baseado na repetição de exercícios e memorização de fórmulas – para uma transformação do ensino de Matemática, mais condizente com a evolução da sociedade contemporânea.
Com a disponibilidade das calculadoras e dos computadores, o ensino de ciências e de matemática deve mudar radicalmente de orientação. Uma vez aceita a calculadora sem restrições, estaria desfeito o nó górdio da educação de hoje. Isto porque a calculadora sintetiza as grandes transformações de nossa era e a entrada de uma nova tecnologia em todos os setores da sociedade. A incorporação de toda a tecnologia disponível no mundo de hoje é essencial para tornar a Matemática uma ciência de hoje (D´AMBRÓSIO, 1999, p. 1-2).
Nesse sentido, as pesquisas em Educação Matemática passam a convergir não para o se, mas para o como se dará o aproveitamento das novas tecnologias. Giraldo (2004), por exemplo, ratifica essa concepção:
a questão a ser investigada não é se a tecnologia é benéfica ao ensino, mas como planejar uma abordagem pedagógica de forma a explorá-la de forma benéfica, fazendo uso positivo de suas potencialidades e limitações (GIRALDO, 2004, p. 46).
Consequentemente, entendemos que o aproveitamento das novas tecnologias – calculadora, planilhas eletrônicas, softwares de geometria dinâmica, plotadores de gráficos e afins – deve ser planejado dentro de um contexto mais amplo, entrelaçado ao planejamento político-pedagógico das escolas e baseado nas Teorias de Aprendizagem atuais, cujos focos estão centrados no aluno. Portanto, o professor pode instigar discussões em relação aos objetos de estudo e utilizar os recursos tecnológicos, por exemplo, para verificação de conjecturas, colaborando para o desenvolvimento de uma das competências específicas da Matemática previstas na BNCC:
Investigar e estabelecer conjecturas a respeito de diferentes conceitos e propriedades matemáticas, empregando recursos e estratégias como observações de padrões, experimentações e tecnologias digitais, identificando a necessidade, ou não, de uma demonstração cada vez mais formal na validação das referidas conjecturas (BRASIL, 2018, p. 523).
Outra vantagem da utilização dos recursos tecnológicos está prevista na BNCC (2018, p. 526), pois essa “... possibilita aos estudantes aprofundar sua participação ativa no processo de resolução de problemas.” Assim, os alunos passam a ser investigadores dos objetos de estudo e têm maior liberdade de formular suas próprias questões. Além disso, as experiências que utilizam recursos tecnológicos “reforçam a capacidade de raciocinar logicamente, formular e testar conjecturas, avaliar a validade de raciocínios e construir argumentações. (BRASIL, 2018, p. 526)”.
A tecnologia, à luz da Educação Matemática Crítica, revela-se como uma ferramenta, não somente para gerar interesse e uma maior participação dos alunos, mas, também, para auxiliar a Matemática a promover a construção de conhecimentos, valores e atitudes, favorecendo os estudantes na sua autonomia como cidadãos diante de uma sociedade cada vez mais automatizada.
Nos cenários que apresentaremos mais adiante, a exploração utilizará de forma intensiva os recursos tecnológicos, em especial, o computador. A abordagem computacional permitirá ao aluno perceber o potencial ganho na aplicabilidade de uma tecnologia digital para resolver problemas experimentais. Ao fazer uso de tecnologias digitais em sala de aula, oportuniza-se um maior aprofundamento, acompanhado de uma melhor compreensão dos resultados do objeto em estudo, mostrando ao aluno uma nova forma de pensar na resolução de uma situação-problema.
3. Aspectos Metodológicos
O “Jogo da Corrida dos Cavalos” é utilizado, nesse trabalho, como ferramenta para a apresentação e exploração de cenários para investigação. Resumidamente, o jogo consiste num tabuleiro com 11 colunas numeradas de 2 a 12 e 6 linhas numeradas de 0 a 5. Onze cavalos ficam dispostos em uma das colunas de 2 a 12, na linha 0, inicialmente. Dois dados usuais e honestos de 1 a 6 são lançados simultaneamente, e a soma dos números das faces voltadas para cima é anotada. O cavalo correspondente a tal número avança uma casa (vai para a linha acima), ganhando o que chegar primeiro na linha 5.
Acerca da terminologia, nesse artigo, uma rodada do “Jogo da Corrida dos Cavalos” refere-se ao processo de lançar os dados e avançar uma casa com o cavalo correspondente à soma obtida, e uma partida consiste em uma execução sucessiva de rodadas, terminada quando um dos 11 cavalos é sorteado cinco vezes.
Skovsmose (2000) descreve o “Jogo da Corrida dos Cavalos” como uma atividade cujo ambiente de aprendizagem faz referência à semirrealidade e como “cenário através do qual os alunos são convidados a fazer explorações e explicações”. Nesse sentido, observamos um caráter dinâmico do jogo, não sendo, simplesmente, um recurso material a ser desenvolvido em sala de aula, mas sim uma atividade lúdica capaz de levar à construção e à consolidação de entendimentos acerca de conceitos matemáticos existentes nele, promovendo uma maior autonomia no pensar crítico dos sujeitos envolvidos e contendo, em si, novos outros cenários possíveis para investigação.
Em “Relato de Experiência: probabilidade no Ensino Médio” (Machado et. al, 2020), verifica-se a aplicabilidade do “Jogo da Corrida dos Cavalos” em escolas públicas nas quais os alunos foram estimulados a participar, ativamente, de todas as etapas, exercitando e/ou construindo de forma lúdica e crítica o seu entendimento sobre conceitos de Probabilidades.
A atividade desenvolvida nos permitiu verificar que os alunos, de forma prática e lúdica, fixaram e expandiram a sua compreensão de conceitos centrais do tema, como: espaços amostrais, equiprobabilidade, frequência relativa x probabilidade, entre outros. Assim, os alunos vivenciaram uma situação real, na qual foram utilizados os conceitos da Teoria das Probabilidades e da Estatística, observando a força desses conceitos na previsão de resultados, numa relação simbiótica entre estabelecer conceitos a partir de um problema dado e, abstratamente, a partir de argumentos lógicos, inferir sobre a situação real. (Machado et. al, p. 249, 2020).
Os resultados pedagógicos obtidos em Machado et. al (2020) foram positivos, uma vez que foi possível perceber uma melhora na compreensão dos conteúdos de probabilidade. Na ocasião da aplicação do “Jogo da Corrida dos Cavalos” em sala de aula, um tabuleiro físico, confeccionado com o auxílio do Grupo de Educação Matemática do CAp-UERJ, foi levado para que os alunos pudessem realizar várias partidas do jogo.
Assim, o presente artigo é uma continuação do trabalho realizado pelos autores junto ao Grupo de Educação Matemática do CAp-UERJ. Nesse trabalho, queremos ressaltar como os aspectos computacionais do “Jogo da Corrida dos Cavalos” permitem novas abordagens investigativas que podem ocasionar Educação Matemática Crítica. Para tanto, desenvolvemos uma versão digital animada do jogo na linguagem Scratch para o desenvolvimento de aspectos lúdicos, bem como uma simulação computacional, em linguagem C++, que exibe as estatísticas associadas aos resultados da simulação, além de possibilitar explorar versões modificadas dele. Cabe mencionar que simulamos a realização de até cem milhões de partidas e guardamos as informações sobre os cavalos vencedores e sobre em qual rodada a partida termina. Para a confecção dos histogramas que serão apresentados na seção a seguir, utilizamos planilhas eletrônicas do LibreOffice e o software Octave. Com esses recursos tecnológicos disponíveis, desenvolvemos três possíveis cenários para investigação dentro do “Jogo da Corrida dos Cavalos”.
Para o presente texto e confecção dos cenários, realizamos a aplicação da metodologia definida por Alrø e Skovsmose (2006, p. 52), que denominam "abordagens investigativas" como sendo o conjunto de metodologias, tais como, a proposição de problemas, a resolução de problemas e trabalho com projetos, que tem como propósito criar oportunidades para a realização de investigações e tornar o aluno um pesquisador dentro e fora de sala de aula. Para isso, realizamos uma investigação qualitativa das potencialidades pedagógicas e do uso de recursos tecnológicos no “Jogo da Corrida dos Cavalos” a fim de ocasionar Educação Matemática Crítica. Essa metodologia serve de contraponto ao paradigma do exercício, bem como rompe com o contrato didático normalmente estabelecido de uma comunicação bancária entre professor-aluno.
Na visão de Alrø e Skovsmose (2006), o ensino tradicional está ligado ao paradigma do exercício, que preconiza a sua repetição a partir de um conhecimento transmitido pelo professor, propiciando pouca oportunidade ao aluno de ressignificar o conteúdo a partir da intuição e investigação. Os cenários, em oposição, são uma oportunidade de tornar o aluno um ator ativo no processo de aprendizagem, porque ele, sob a supervisão do professor, passa a agir ativamente para construir estratégias que levem a uma resposta concreta, baseada em critérios lógicos que foram postos à prova.
Portanto, pelos motivos acima expostos, a escolha dessa metodologia foi fundamental para a proposição dos cenários do presente trabalho, uma vez que esses possibilitam encaminhamentos em sala de aula e abrem, a partir de uma perspectiva metodológica, consolidada na literatura, espaço para o pensamento crítico, investigativo e reflexivo. Nesse contexto, o trabalho cooperativo e, consequentemente, o diálogo são partes constituintes fundamentais da investigação. Logo, é sob essas óticas que os autores localizam suas proposições de atividades na seção a seguir.
4. Discussão sobre as possibilidades educacionais do jogo
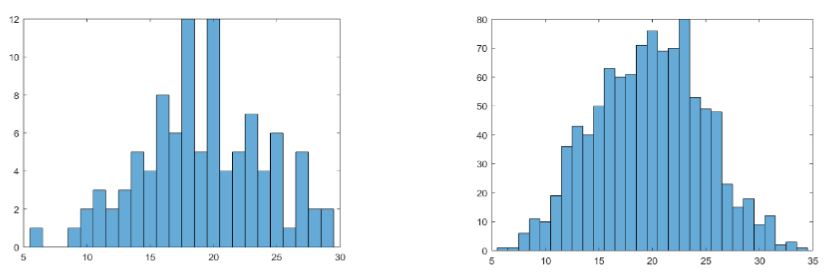
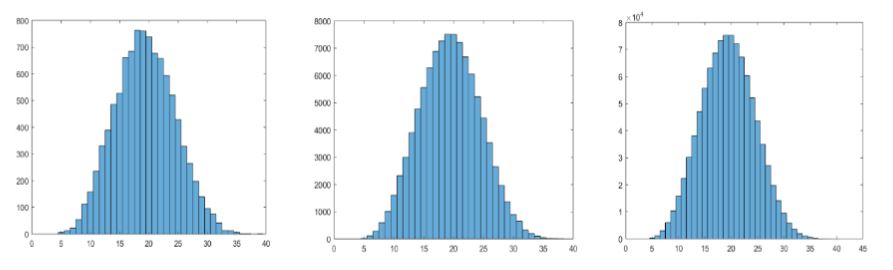
Antes de explorarmos os cenários para investigação propostos, destacaremos uma característica do uso de uma simulação computacional numa abordagem investigativa que envolva o “Jogo da Corrida dos Cavalos”. Quando se joga em um tabuleiro físico, existe uma limitação natural quanto ao número de partidas jogadas, que não ocorre no contexto computacional. As Figuras 1 e 2 mostram a frequência de partidas finalizadas em uma determinada rodada à medida que o número delas aumenta. É possível perceber que, com 10.000 partidas, o gráfico apresenta um formato que se repete nos gráficos seguintes, indicando que as frequências relativas estão mais próximas do valor teórico da probabilidade. No entanto, jogar dez mil partidas seria impraticável em sala de aula. Dessa forma, o uso do computador permite que novas informações sejam acessadas.
Como podemos observar na Tabela 2, a seguir, o tempo necessário para realização de 1 milhão de partidas é bem pequeno se comparado ao tempo de realização de apenas uma partida em tabuleiro físico:
| Partidas | 100 | 1.000 | 10.000 | 100.000 | 1.000.000 | 10.000.000 | 100.000.000 |
| Tempo (s) | <0,001 | 0,001 | 0,011 | 0,087 | 0,847 | 8,504 | 80,084 |
O potencial ganho da implementação tecnológica demonstra como o uso de recursos computacionais contribui com a própria condução de ensino e aprendizagem por meio da pesquisa investigativa com cenários, visto que, sem o computador, seria impraticável fazê-la. Embora o incentivo ao uso não seja simples e exija bastante trabalho, especialmente, no planejamento das atividades, essa ação faz-se necessária em um contexto mundial de popularização das tecnologias digitais. Assim, esses recursos podem e devem ser utilizados como instrumento de pesquisa em sala de aula.
Haja vista o acima exposto, apresentaremos três cenários para investigação que podem ser explorados no “Jogo da Corrida dos Cavalos”, incentivando o uso de recursos tecnológicos como aliado para a resolução de problemas de Matemática. Cabe mencionar que, dentro de cada um desses cenários, estão sugeridos problemas que podem ser utilizados pelo professor ao aplicar a atividade.
No cenário 1, vamos estudar os diferentes espaços amostrais para o mesmo problema e apresentar como isso pode ser rico para repensar estratégias na busca de soluções. No cenário 2, estudamos as probabilidades de um jogo terminar em uma determinada rodada e discutimos como o número de casos envolvidos aumenta rapidamente, à medida que o número de rodadas torna-se maior. No cenário 3, estudamos as probabilidades de um cavalo ser o vencedor da partida.
A aplicação desses cenários em sala de aula conduz o aluno a pensar por si mesmo, adquirindo autonomia crítica, contrapondo-se ao que o ocorre na mera resolução de exercícios. Nesses cenários, abrangemos as seguintes habilidades previstas na BNCC:
Resolver e elaborar problemas que envolvem o cálculo da probabilidade de eventos aleatórios, identificando e descrevendo o espaço amostral e realizando contagem das possibilidades. [...] Resolver e elaborar problemas que envolvem o cálculo de probabilidade de eventos em experimentos aleatórios sucessivos. [...] Reconhecer a existência de diferentes tipos de espaços amostrais, discretos ou não, de eventos equiprováveis ou não, e investigar as implicações no cálculo de probabilidades. [...] Utilizar noções de probabilidade e incerteza para interpretar previsões sobre atividades experimentais, fenômenos naturais e processos tecnológicos, reconhecendo os limites explicativos das ciências. (BRASIL, 2018, p. 529, 533 e 543).
Ressalta-se que o jogo, nesse trabalho, é utilizado como uma ferramenta didática para o aprendizado de Probabilidade e Estatística. As questões e discussões levantadas nesses cenários são apresentadas, em alguns momentos, simulando-se um ambiente de sala de aula, ora sugerindo perguntas que podem ser feitas pelos alunos, ora mostrando questionamentos que o professor pode realizar na condução da atividade. Assim, o objetivo é utilizar técnicas e conteúdos que podem ser inseridos no ensino básico para explorar as situações que surgem.
Ao separar a análise do jogo em cenários, não pretendemos impor uma ordem na investigação, e sim sugerir uma possível organização para o estudo da atividade. Naturalmente, os cenários propostos têm interseções, por exemplo: ao discutir o espaço amostral do problema, no cenário 1 de investigação, é possível que os alunos levantem a questão do número mínimo e máximo de rodadas, assunto pertencente ao cenário 2. Em nosso entendimento, o professor não deve restringir esse tipo de discussão, porque, por definição, cenários para investigação estimulam o aluno a pensar e conjecturar livremente. Portanto, não seria adequado limitar os questionamentos e reflexões ao conteúdo específico do cenário que está sendo trabalhado.
4.1 Primeira possibilidade de Cenário para Investigação: Espaços Amostrais
O cálculo da probabilidade de um cavalo avançar uma casa em uma rodada é o primeiro passo na investigação do jogo. Para determinar essas probabilidades, o professor pode iniciar discutindo quais são os possíveis resultados quando dois dados são lançados. Assim, podemos ter como espaço amostral das rodadas o conjunto .
Uma pergunta provocante pode surgir nesse momento: esse espaço amostral é equiprovável? Os alunos que responderem que o espaço não é equiprovável podem estar se baseando no fato de que algumas somas aparecem em diferentes quantidades: a soma 7, por exemplo, aparece seis vezes, enquanto a soma 2, apenas uma vez. Porém, cada um dos 36 resultados do espaço amostral tem a mesma probabilidade de ocorrer, a qual vale pelo princípio multiplicativo:. Portanto, é um espaço amostral equiprovável.
As probabilidades , em que é a probabilidade do cavalo avançar uma casa no tabuleiro, são calculadas observando-se todos os pares ordenados de cuja soma das coordenadas é igual a , obtendo-se a Tabela 3 abaixo:

De modo a aprofundar a discussão, a Tabela 3 pode ser usada para iniciar a questão da unicidade do espaço amostral. Já foi visto que é um espaço amostral equiprovável para a análise de uma rodada. Entretanto, a Tabela 3 sugere que , também, pode ser considerado um espaço amostral para as rodadas, sem ser, porém, um espaço amostral equiprovável.
A determinação das probabilidades é fundamental para a análise do jogo, bem como a determinação de , mas ainda é preciso encontrar um espaço amostral para uma partida do “Jogo da Corrida dos Cavalos”. Portanto, direcionaremos nossa atenção para o questionamento: “Como determinar um espaço amostral para uma partida do Jogo da Corrida do Cavalos?”
Se considerarmos que, no experimento aleatório, deseja-se observar “o cavalo vencedor”, podemos ter como espaço amostral o conjunto . Cabe ressaltar que, embora os conjuntos e sejam iguais, as probabilidades dos seus eventos elementares ocorrerem são distintas, como mostraremos mais adiante, e isso ocorre porque esses espaços amostrais se referem a situações diferentes. Assim, a pergunta que surge, naturalmente, é: como calcular a probabilidade dos eventos elementares de ? Esse problema não é simples de ser resolvido manualmente, em função do grande número de casos envolvidos. Assim, no cenário 3, essa questão será discutida detalhadamente. Nesse momento, a investigação pode ser orientada no sentido de fazer o aluno perceber que, para calcular, por exemplo, a probabilidade de vitória do cavalo 2, seria preciso encontrar todas as partidas em que o cavalo 2 é o vencedor.
Alternativamente, se no experimento deseja-se observar “qual partida ocorreu”, os elementos desse novo espaço amostral poderiam ser representados por sequências da forma em que representa o cavalo que foi sorteado na rodada com e e é o número de rodadas da partida. Nesse caso, o professor pode apresentar como calcular a probabilidade dos eventos elementares que compõem esse espaço amostral. Como exemplo, pode-se expor a partida representada pela sequência (7, 7, 6, 7, 4, 7, 7), em que sua probabilidade pode ser calculada usando o princípio multiplicativo, uma vez que os valores sorteados nas diferentes rodadas são independentes. Assim, .
O professor pode indagar, novamente, nesse contexto, sobre a questão de equiprobabilidade. Para demonstrar que não estamos em uma situação de espaço amostral equiprovável, o docente pode selecionar outra partida e calcular sua probabilidade. Por exemplo, considerando-se a sequência (5,7,5,5,5,5), tem-se que. Assim, e, portanto, esse não é um espaço amostral equiprovável. Logo, a discussão pode ser orientada no sentido de avaliar qual dos dois espaços amostrais é mais adequado, ou mais conveniente, para o estudo do jogo.
4.2 Segunda possibilidade de Cenário para Investigação: Número de Rodadas
Dentre as questões que o professor pode apresentar, encontram-se o número mínimo de rodadas possíveis em uma partida (cinco), o número máximo de rodadas (45) ou, ainda, uma discussão sobre em quais rodadas é mais provável ocorrer o término da partida.
Após as discussões iniciais sobre elas, a investigação pode ser aprofundada por meio de questionamentos realizados pelo docente. Por exemplo, em relação ao número mínimo de rodadas, pode-se propor a seguinte questão: “Qual é a probabilidade de a partida terminar na 5ª rodada?”
Para responder à pergunta, os alunos deverão pensar em todas as situações possíveis em que a partida termina na 5ª rodada. Ao refletir sobre elas, deverá perceber que a única forma de o cavalo i vencer na 5ª rodada é se a soma i sair cinco vezes consecutivas nos lançamentos dos dados.
Portanto, o aluno deve concluir que, para cada cavalo i, a probabilidade de i vencer na quinta rodada é, pelo princípio multiplicativo, (pi)5. Em seguida, ao verificar que os eventos são mutuamente exclusivos, ele perceberá que deve somar todas as probabilidades para obter a probabilidade de a partida terminar na 5ª rodada: em que é a probabilidade de a partida terminar na -ésima rodada, sendo .
É importante que o professor, antes de realizar os cálculos que conduzem à resolução, inquira os alunos sobre a resposta que esperam obter (“é pouco provável que a partida termine na 5ª rodada?”). Após a obtenção dessa probabilidade, é cabível retomar a discussão sobre quão provável é que a partida termine na 5ª rodada em face do valor encontrado.
O cálculo exato da probabilidade realizado acima pode fazer com que surja a questão da probabilidade de término em uma rodada qualquer. Se foi possível calcular a probabilidade de término na 5ª rodada, por que não calcular a probabilidade de término em uma rodada qualquer? Nesse momento, o professor pode explorar, junto aos alunos, as dificuldades que surgem quando se deseja calcular a probabilidade do término da partida ocorrer em outras rodadas. É válido, assim, propor a seguinte questão: “É possível calcular , com ?”
Nesse ínterim, pode ser interessante que o docente explique o caso , de forma a apresentar como o número de eventos envolvidos aumenta de forma rápida. Para resolvê-lo, o aluno deve perceber, inicialmente, que a partida terminará na rodada 6 somente se algum dos cavalos se tornar o vencedor da partida nessa rodada, assim como no caso da rodada 5, e que as diferentes formas de isso ocorrer são mutuamente exclusivas. Daí, utilizando o princípio aditivo, ele poderá deduzir que a probabilidade de a partida terminar na sexta rodada é , onde é a probabilidade do cavalo ser vencedor da partida na rodada , com e .
De forma intuitiva, a partida termina na rodada 6 quando o cavalo 2 se torna o vencedor da partida na rodada 6, ou o cavalo 3 se torna o vencedor da partida na rodada 6, e assim por diante, até a alternativa em que o cavalo 12 se torne o vencedor da partida na rodada 6. O docente pode aproveitar esse momento para deduzir, por analogia, a fórmula geral para o cálculo de probabilidade para uma rodada qualquer: .
Voltando ao caso , os alunos deverão pensar em como calcular para . Para orientar a discussão, o docente pode indicar como exemplo o cavalo 2 e analisar com os alunos as diferentes maneiras em que esse cavalo pode ser o vencedor da partida na rodada 6. Com o auxílio de uma planilha, é cabível que o professor relate algumas das formas em que o cavalo 2 é o vencedor, como as sequências (2,2,7,2,2,2), (5,2,2,2,2,2) e (2,2,2,2,6,2). As probabilidades dessas partidas podem ser calculadas pelo princípio multiplicativo:
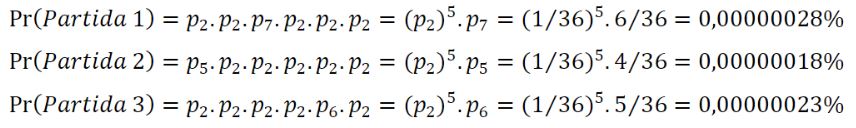
Entretanto, não parece viável enumerar todas as partidas em que o cavalo 2 vence na 6ª rodada, calcular suas probabilidades e, em seguida, somá-las. A discussão pode, portanto, ser orientada no sentido de obter uma maneira de encontrar a quantidade de partidas em que esse cavalo vence na rodada 6.
De forma geral, o cavalo 2 será vencedor quando, na 6ª rodada, o valor “2” aparecer, e, nas outras 5 rodadas, tivermos 4 valores iguais a “2” e um valor X (diferente de 2), como indicado na Tabela 4:
| Rodada 1 | Rodada 2 | Rodada 3 | Rodada 4 | Rodada 5 | Rodada 6 | |
| Partida | 2 | 2 | 2 | X | 2 | 2 |
Fixada a quarta posição para X, como exemplificado pela Tabela 4, a probabilidade de uma partida desse modelo ocorrer é , em que é a probabilidade de ocorrer um número diferente de 2, pelo princípio aditivo ou pela probabilidade de eventos complementares.
De quantas maneiras podemos escolher uma posição para X? Raciocinando em termos de permutação com repetição, temos 5 cavalos, com um deles aparecendo 4 vezes (o cavalo 2 da rodada 6 já está fixo e não precisa ser considerado no cálculo das permutações). O número de permutações é, portanto, .
Assim, existem cinco formas de distribuir esses cinco cavalos (quatro vezes o cavalo 2 e uma vez um cavalo diferente de 2) nas primeiras 5 rodadas. A probabilidade dessas partidas é, assim, . Substituindo os valores na igualdade acima, temos .
Para responder à pergunta inicial (“qual a probabilidade de a partida terminar na 6º rodada?”), é preciso realizar o mesmo procedimento para os demais cavalos. As probabilidades para os outros cavalos estão apresentadas na Tabela 5:

Assim, a probabilidade de a partida terminar na rodada 6 é. Esse número expressa, intuitivamente, a expectativa de que, a cada mil partidas, o jogo terminará na sexta rodada, aproximadamente, uma vez.
Após o cálculo da probabilidade acima, o professor pode chamar a atenção para o aumento da complexidade quando se passou da 5ª para a 6ª rodada. Porém, apesar desse aumento, ainda foi possível calcular as probabilidades envolvidas. Para convencer os alunos sobre a dificuldade do problema, o docente poderia iniciar a discussão sobre o caso .
O início da sua argumentação pode ser do mesmo modo que as discussões anteriores, isso é, analisando partidas em que um determinado cavalo, como o 2, é o vencedor. Por exemplo, a partida que corresponde à sequência (4,7,7,2,2,2,6,3,2,2), pelo princípio multiplicativo, tem probabilidade igual a .
A dificuldade do problema fica aparente quando se objetiva calcular a quantidade de maneiras em que o cavalo 2 pode ser o vencedor em 10 rodadas. De forma geral, para o cavalo 2 ser o vencedor em 10 rodadas, deve-se ter uma situação como a indicada na Tabela 6 abaixo:
| Rodadas (1, ... , 9) | Rodada 10 | |
| Partida | (2, 2, 2, 2, X, Y, Z, W, T) | 2 |
As letras X, Y, Z, W e T da Tabela 6 indicam cavalos diferentes do cavalo 2. A mudança desse caso para os anteriores é a de que, nessa ocorrência, devemos garantir que não ocorra a situação de um outro cavalo sair cinco vezes antes do cavalo 2. Ou seja, se X = Y = Z = W = T, um cavalo diferente estaria sendo o vencedor. Essa discussão evidencia o aumento de complexidade da análise quando se aumenta o número de rodadas. Observe que o problema de múltiplos vencedores aparece a cada 5 rodadas: com 15 rodadas, é preciso tomar cuidado para que não haja 3 cavalos vencedores; com 20 rodadas, 4 cavalos, e assim por diante. Portanto, fica constatado que abordar esse problema analiticamente não é tarefa simples.
Após a verificação da complexidade de se realizar os cálculos manualmente, o docente pode apresentar os histogramas gerados a partir da simulação computacional e realizar uma discussão sobre em quais rodadas são mais prováveis de ocorrer o término da partida.
Como apresentam as figuras 1 e 2, à medida que aumenta a quantidade de partidas simuladas, o histograma tende a se “estabilizar”, no sentido de tornar mais previsíveis os resultados obtidos. As primeiras imagens (Figura 1) têm um comportamento irregular, modificando-se bastante entre um histograma e outro. Contrariamente, o segundo grupo de imagens (Figura 2) têm histogramas mais parecidos, indicando que a probabilidade de o jogo terminar em uma determinada rodada (estimada a partir do histograma pela frequência dividida pelo número total de partidas) é mais próxima do valor teórico. Esse resultado empírico é uma expressão da Lei Forte dos Grandes Números de Borel: se é o número de vezes que o evento ocorre nas primeiras repetições, então , onde denota a probabilidade do evento (WEN, 1991).
4.3 Terceira possibilidade de Cenário para Investigação: Cavalo Vencedor
Iniciar esta investigação buscando calcular diretamente a probabilidade de um cavalo qualquer ser o vencedor pode ser complexo, como discutiremos, detalhadamente, mais adiante, porém situações simplificadas podem ser exploradas. Por exemplo, o docente pode propor a seguinte situação: “Se o cavalo 12 for colocado na casa 4 e o cavalo 7 estiver na casa 0, qual dos dois cavalos tem mais probabilidade de vencer a partida?”
O professor deve deixar claro que, nesse contexto, apesar de usarmos os dados usuais, os demais cavalos serão ignorados. Os alunos devem perceber que algumas mudanças foram introduzidas nessa situação simplificada: primeiramente, o espaço amostral do problema foi modificado, uma vez que os outros cavalos não estão sendo considerados. Além disso, não é possível determinar o número máximo de rodadas, pois podem ocorrer sequências arbitrariamente longas de valores que não sejam 7 ou 12.
Assim como na discussão da versão completa do jogo, nessa versão simplificada, os alunos terão que procurar a probabilidade de os cavalos 7 ou 12 vencerem a partida, guiando-se pela probabilidade de sair o 7 ou o 12 em uma rodada. Do mesmo modo que no jogo normal, existem 6 formas de sair a soma 7 e apenas uma forma de sair a soma 12. Nessa nova situação, entretanto, podemos desprezar os demais resultados, e, portanto, o docente (ou os alunos) pode sugerir que e .
Alguns alunos podem não ter certeza se essa abordagem está correta, mas o docente deve aqui exercer o seu papel de motivador e incentivar os alunos a prosseguirem com seu raciocínio, confrontando, dialogicamente, as diferentes ideias de modo a buscar a verdade científica. Seguindo a discussão nessa mesma linha de raciocínio, os alunos devem perceber que o cavalo 7 será o vencedor apenas se ele sair 5 vezes seguidas (isto é, sem sair o 12 uma única vez). O problema pode, nessa ocasião, ser resolvido usando o princípio multiplicativo , em que é a probabilidade do cavalo vencer a partida. A probabilidade do cavalo 12 vencer pode ser calculada utilizando a ideia de eventos complementares:.
Nesse momento, o docente pode apresentar os resultados da simulação computacional dessa versão simplificada do jogo e confrontar os resultados da teoria com os resultados advindos da simulação: ao executar 100.000 partidas desse jogo, o cavalo 7 foi o vencedor em 46,27% das partidas, e o cavalo 12 venceu em 53,73% das partidas, validando os resultados anteriores.
Se o aluno tinha dúvidas quanto à estratégia usada, o resultado da simulação fortalecerá a confiança no raciocínio utilizado para a resolução dessa situação. Além disso, caso um aluno tenha estabelecido alguma outra estratégia teórica, a simulação computacional pode confirmá-la ou indicar que tal estratégia necessita de algum ajuste.
Há diversas provocações que o professor pode fazer aos alunos. Pode pedir, por exemplo, que eles tentem encontrar algumas propriedades de como a probabilidade é distribuída entre os cavalos. Diante da tarefa, comentários podem surgir, como: não é surpreendente que o cavalo 12 tenha mais chance de ganhar o jogo, mesmo tendo seis vezes menos chance de sair? Outro aspecto que pode ser explorado e pode surgir durante a aplicação do jogo na versão completa é a questão da simetria das probabilidades entre pares de cavalos. Na Tabela 3, pode-se perceber que os cavalos 2 e 12 têm a mesma probabilidade de avançar em uma rodada, assim como ocorre com os pares 3 e 11, 4 e 10, 5 e 9, 6 e 8. Na Figura 2, vemos que essa simetria se mantém nas frequências das vitórias desses pares de cavalos.
Portanto, para orientar a discussão com uma questão mais simples, o docente pode fazer uma pequena mudança na situação anterior e propor a seguinte questão: “Se os cavalos 2 e 12 forem colocados na casa 4, e o cavalo 7 estiver na casa 0, como ficarão as probabilidades de vitória para cada cavalo?”
Intuitivamente, devido à simetria existente entre os cavalos 2 e 12, espera-se obter um resultado similar ao encontrado anteriormente, mas com os cavalos 2 e 12 “dividindo ao meio” as suas probabilidades de vitória. Nesse caso, passamos a ter um espaço amostral com três elementos: 2, 7 e 12. Racionando de forma análoga à resolução do problema anterior, existem seis formas de obter a soma 7, uma forma de obter a soma 2 e uma forma de obter a soma 12 e, portanto, existem 8 somas possíveis. Assim, é razoável supor que , e . Desse modo, a probabilidade do cavalo 7 vencer a partida é: . Consequentemente, pela complementariedade do problema, temos:. Novamente, a simulação permite aumentar a confiança no raciocínio matemático utilizado.
Para avançar na discussão das dificuldades matemáticas do jogo, retornamos à questão da probabilidade de um cavalo ser vencedor com uma nova situação: “Se o cavalo 12 for colocado na casa 3 e o cavalo 7 estiver na casa 0, qual dos dois cavalos tem mais probabilidade de vencer a partida?”
Nesse caso, o aluno perceberá que, ao introduzir uma pequena mudança, o número de casos já sofreu um aumento considerável. Agora, o cavalo 7 pode ser o vencedor mesmo que o cavalo 12 seja sorteado (desde que em apenas uma rodada). Portanto, uma das formas do cavalo 7 vencer é no caso em que a soma 7 é obtida cinco vezes seguidas, ou seja, que ocorra a partida (7, 7, 7, 7, 7), e a outra forma do cavalo 7 ser vencedor ocorre em qualquer partida que apresente a seguinte disposição (Tabela 7):
| Rodada 1 | Rodada 2 | Rodada 3 | Rodada 4 | Rodada 5 | Rodada 6 | |
| Partida 2 | 7 | |||||
| (7, 7, 7, 7, 12) | ||||||
A probabilidade da primeira partida já foi calculada anteriormente e todas as partidas do 2º caso têm a mesma probabilidade de ocorrer, qual seja . Mas quantas partidas desse tipo podem ocorrer? Novamente, deve-se utilizar a ideia de permutação com repetição: temos 4 elementos iguais a 7 e um igual a 12. Logo, existem partidas possíveis. Portanto, a probabilidade do cavalo 7 vencer na sexta rodada vale e somando as probabilidades, temos que . Em relação à probabilidade do cavalo 12 ser o vencedor, ela pode ser calculada usando a ideia de eventos complementares . Observe que, colocando o cavalo 12 apenas uma casa atrás em comparação a situação simplificada inicial desse cenário, a probabilidade do cavalo 12 ser o vencedor é, significativamente, menor.
Ao se propor questões simplificadas, espera-se que o aluno ganhe um entendimento maior sobre a versão completa do jogo e, além disso, exercite seu raciocínio e intuição ao defrontar com as mudanças realizadas. Observe que, nessas simplificações do jogo, ele foi obrigado a repensar o espaço amostral do experimento, bem como as probabilidades envolvidas.
Após as investigações das questões expostas anteriormente, objetiva-se que o aluno tenha desenvolvido um bom entendimento sobre as propriedades e dificuldades de calcular a probabilidade de um cavalo ser o vencedor da partida, além de ter alcançado uma maior intuição sobre como é o comportamento do jogo e como os problemas de contagem de casos (de ordem fatorial) podem crescer rapidamente. Pode-se então, finalmente, propor a seguinte questão: “ual a probabilidade do cavalo 2 vencer a partida?”
Nesse nível, deve estar claro que a resolução dessa probabilidade exige que se calcule a probabilidade de o cavalo 2 vencer em qualquer uma das rodadas possíveis. Em outras palavras, o cavalo 2 é o vencedor se for o vencedor na 5ª rodada, ou na 6ª rodada, ou na 7ª rodada, e assim por diante, até a 45ª rodada.
Nesse momento, pode ser retomada a discussão sobre rodadas. Foi visto que, a partir da 10ª rodada, o cálculo da probabilidade não é simples, com a dificuldade aumentando a cada 5 rodadas, tornando inviável a resolução do problema por meio das técnicas utilizadas até aqui. Como alternativa, o uso da simulação computacional permite que o jogo seja realizado um número muito grande de vezes, em um tempo curto, gerando valores empíricos para as probabilidades.
Os valores obtidos na simulação da versão completa do jogo podem agora ser apresentados (Tabela 8):
| Número de partidas simuladas | |||||||
| Cavalo | 100 | 1.000 | 10.000 | 100.000 | 1.000.000 | 5.000.000 | 10.000.000 |
| 2 | 0,000 | 0,000 | 0,050 | 0,059 | 0,050 | 0,050 | 0,050 |
| 3 | 2,000 | 0,900 | 0,740 | 0,862 | 0,878 | 0,886 | 0,885 |
| 4 | 3,000 | 3,000 | 3,720 | 3,888 | 3,877 | 3,882 | 3,877 |
| 5 | 11,000 | 9,600 | 9,800 | 9,813 | 9,882 | 9,909 | 9,899 |
| 6 | 20,000 | 20,200 | 19,630 | 19,448 | 19,331 | 19,323 | 19,324 |
| 7 | 33,000 | 31,200 | 32,080 | 32,049 | 32,002 | 31,982 | 31,964 |
| 8 | 14,000 | 19,100 | 19,130 | 19,181 | 19,250 | 19,291 | 19,299 |
| 9 | 13,000 | 10,600 | 10,000 | 9,845 | 9,894 | 9,879 | 9,894 |
| 10 | 2,000 | 4,500 | 3,930 | 3,938 | 3,898 | 3,863 | 3,871 |
| 11 | 2,000 | 0,900 | 0,900 | 0,857 | 0,886 | 0,884 | 0,887 |
| 12 | 0,000 | 0,000 | 0,020 | 0,060 | 0,052 | 0,051 | 0,050 |
A Tabela 8 expõe a frequência relativa de vitórias quando são executadas de 100 a 10.000.000 de partidas. É possível notar que a frequência de vitórias de todos os cavalos tende a se estabilizar ao longo das execuções. É provável que nas discussões iniciais tenha sido conjecturado que o cavalo 7 venceria o maior número de partidas, uma vez que tem a maior probabilidade de avançar em uma rodada. Os resultados obtidos pela simulação comprovam essa conjectura: o cavalo 7 foi quem mais ganhou, sendo o vencedor em cerca de 32% das partidas. Além disso, o professor também pode ressaltar a simetria presente na Tabela 8: os pares de cavalos equidistantes do 7 venceram (aproximadamente) o mesmo número de partidas (os cavalos 6 e 8, por exemplo, foram vencedores em cerca de 19% das partidas). Esse resultado também é intuitivo, uma vez que esses pares apresentam a mesma probabilidade de avançar uma casa em cada rodada do jogo.
Porém, cabe ressaltar o seguinte fato: em questões anteriores, a simulação foi utilizada para confirmar os resultados obtidos pela resolução analítica dos problemas. Aqui, entretanto, a estratégia concreta foi utilizar o computador como uma ferramenta na obtenção das frequências e estimativas para as probabilidades de vitórias. Dessa forma, a abordagem computacional apresentada ocasiona um ganho potencial do uso da tecnologia em sala de aula, visto a sua característica exploratória.
Respondida a pergunta principal do jogo (“qual a probabilidade de vitória para cada cavalo?”), novas situações podem ser exploradas. Nesse nível, a expectativa é a de que os alunos já tenham levantado diversas situações: “E se os cavalos estivessem do jeito...?”, “Existe alguma configuração para uma versão simplificada que aumenta as chances de vitória dos outros cavalos?” Essa perspectiva torna a aula muito dinâmica e criteriosa, o que é compatível com uma pesquisa científica, pois o aluno não recebe respostas prontas e atua ativamente na construção dos saberes.
Portanto, entendendo que os cenários para investigação não se esgotam nas situações descritas, oferecemos suporte para que o professor, no momento da aula, possa explorar novas situações no “Jogo da Corrida dos Cavalos”, acessando o blog e fazendo uso da simulação disponibilizada naquele ambiente.
5 Considerações Finais
Neste artigo, apresentamos e exploramos as possibilidades educacionais para a ocorrência de cenários para investigação, por meio do jogo denominado “Jogo da Corrida dos Cavalos”, produzido pelos autores que se baseiam nas ideias de Skovsmose (2000), de modo que possam ocasionar a Educação Matemática Crítica, discutindo-as para sua utilização em sala de aula e exibindo o potencial ganho do uso de recursos computacionais, caso sejam propostas aos alunos.
O estudo das questões levantadas dentro dos cenários foi realizado de forma investigativa e exploratória, na qual as respostas foram construídas progressivamente, analisando-se diferentes estratégias de resolução, conforme preconiza a BNCC. Os cenários permitem discutir diversos aspectos dos eixos temáticos da Probabilidade e Estatística como espaços amostrais, equiprobabilidade, lei forte dos grandes números, entre outros.
Os recursos tecnológicos, em especial o computador, foram utilizados de forma intensa nas investigações. Devido às características do jogo, muitas questões têm uma abordagem analítica complexa. Assim, os dados obtidos a partir da simulação computacional implementada foram fundamentais para que um melhor entendimento sobre essas questões fosse obtido. Como exemplo, o cálculo da probabilidade de um determinado cavalo ser o vencedor de uma partida foi tratado somente por meios computacionais. Em outras situações, o computador foi utilizado para confirmar as conjecturas levantadas.
Ao propor atividades investigativas com uso de recursos computacionais, buscamos sugerir novas formas de pensar e compreender as soluções dos problemas envolvidos no presente artigo, a fim de desenvolver uma autonomia crítica no pensar e no conjecturar, conduzindo, assim, os sujeitos envolvidos a uma Educação Matemática Crítica numa possível aplicação desses cenários em sala de aula. Além disso, as ferramentas disponibilizadas no blog dos autores (simulação computacional e versão digital) possibilitam que professores e alunos realizem investigações dentro e fora da sala de aula, podendo ocasionar uma maior integração entre conhecimento matemático, ensino e tecnologias digitais. Como trabalhos futuros, acreditamos que essa abordagem computacional do jogo pode ser utilizada para aprofundar o pensamento computacional dos estudantes. Em um próximo trabalho, pretendemos aproximar os alunos dos conceitos utilizados na implementação da simulação computacional, estimulando, assim, seu pensamento algorítmico e sua capacidade de resolução de problemas.
6 Referências
ALRØ, H.; SKOVSMOSE, O. Diálogo e Aprendizagem em Educação Matemática. 2. ed. São Paulo: Autêntica, 2006.
BRASIL. Ministério da Educação. Secretaria de Educação Básica. Base Nacional Comum Curricular: ensino médio. Brasília: MEC, 2018.
BORBA, M. C.; VILLARREAL, M. E. Humans-with-Media and the Reorganization of Mathematical Thinking: Information and Communication Technologies, Modelling, Experimentation and Visualization. 1. ed. Estados Unidos: Springer, 2005.
D’AMBRÓSIO, U. Informática, Ciências e Matemática. 1999.
FREIRE, P. Pedagogia do Oprimido. 1. ed. Rio de Janeiro: Paz e Terra, 1970.
GIRALDO, V. Descrições e Conflitos Computacionais: O Caso da Derivada. 2004. 221f. Tese (Doutorado em Engenharia de Sistemas e Computação) – Universidade Federal do Rio de Janeiro. Rio de Janeiro.
MACHADO, Leandro da Silva; MUSMANNO, Leonardo Maricato; ALMEIDA, Moisés Ceni; SOUSA, Sérgio Gonçalves. Relato de Experiência: Probabilidade no Ensino Médio. EMR, Brasília, v.25, n. 66, p. 239 – 250. 2020.
SKOVSMOSE, Ole. Cenários para investigação. Tradução de Jonei Cerqueira Barbosa. Bolema, Rio Claro, v. 13, n. 14, p. 66-91, 2000.
SKOVSMOSE, O. Educação Matemática Crítica: a questão da democracia. 3. ed. Campinas: Papirus, 2001.
SKOVSMOSE, O. Educação Matemática Crítica: incerteza, matemática, responsabilidade. 1. ed. São Paulo: Cortez, 2006.
SKOVSMOSE, O. Desafios da reflexão em educação matemática crítica. 1. ed. Campinas: Papirus, 2008.
TERES, S. L. L. Em Direção à Educação Matemática Crítica: A análise de uma experiência de Modelagem pautada na Investigação e no uso da Tecnologia. 2014. 199f. Dissertação (Mestrado em Educação). Universidade do Vale do Itajaí. Itajaí.
WEN, Liu. An Analytic Technique to Prove Borel's Strong Law of Large Numbers. The American Mathematical Monthly. Londres. v. 98, n. 2, p. 146-148, 1991.
Notas
Ligação alternative
https://revistapos.cruzeirodosul.edu.br/index.php/rencima/article/view/2899/1551 (pdf)

