



Resultado de investigación
Método heurístico de George Pólya en la resolución de problemas matemáticos en estudiantes de grado sexto
Heuristic method of George Polya in the solving mathematical problems in sixth grade students
Método heurístico de George Pólya na resolução de problemas matemáticos, em alunos do sexto ano
Revista UNIMAR
Universidad Mariana, Colombia
ISSN: 0120-4327
ISSN-e: 2216-0116
Periodicidad: Semestral
vol. 38, núm. 2, 2020
Recepción: 03 Agosto 2020
Aprobación: 21 Octubre 2020

Resumen: El Método heurístico de George Pólya en la resolución de problemas matemáticos es la base y el motivo de la investigación. El estudio está dirigido a estudiantes de grado sexto de la Institución Educativa San Luís Gonzaga del municipio de Túquerres; en este estudio se tomó el desarrollo del pensamiento numérico y las relaciones al aplicar operaciones combinadas para resolver problemas. La metodología es cualitativa naturalista, con enfoque constructivista y tipo descriptivo comprensivo. El estudio permitió conocer y comprender las realidades de las acciones humanas en virtud a la problemática formulada. Se utilizó como instrumentos de recolección de datos, la prueba de conocimiento, cuestionario de la prueba, un taller de uso y aplicación, un taller de evaluación, cuestionario y diario de campo, aplicado a los doce estudiantes de la muestra. Como resultado se obtuvo que, desde la perspectiva heurística, el docente es el actor educativo fundamental, capaz de diagnosticar y detectar las situaciones prácticas, como protagonista de la acción educativa. En conclusión, los hallazgos encontrados fortalecen el proceso de enseñanza y aprendizaje de las matemáticas y así, permiten identificar las políticas y lineamientos que se debe seguir en la institución educativa.
Palabras clave: resolución de problemas, método, enseñanza, aprendizaje, constructivismo.
Abstract: The heuristic method of George Polya in solving mathematical problems is the basis and reason for the investigation. The study is aimed at sixth grade students from the San Luis Gonzaga Educational Institution in the municipality of Túquerres, noting the development of numerical thinking and relationships, when applying combined operations, at the time of solving problems. The methodology is qualitative naturalistic with a constructivist approach and a comprehensive descriptive type. The study allowed to know and understand the realities of human actions by virtue of the formulated problem. The data collection instruments used were the knowledge test, the test questionnaire, a use and application workshop, an evaluation workshop, a questionnaire and a field diary applied to the twelve students in the sample. The results indicate that from the heuristic perspective, the teacher is the fundamental educational actor, capable of diagnosing and detecting practical situations as the protagonist of educational action. In conclusion, the findings discovered strengthen the process of teaching and learning mathematics to identify the policies and guidelines that must be followed in the Educational Institution.
Keywords: Problems solving, method, teaching, learning, constructivism.
Resumo: O método heurístico de George Pólya na resolução de problemas matemáticos é a base e a razão da investigação. O estudo destina-se a alunos do sexto ano do Instituto de Ensino San Luís Gonzaga do município de Túquerres, observando o desenvolvimento do pensamento e das relações numéricas, na aplicação de operações combinadas, na hora de resolver problemas. A metodologia é qualitativa naturalística com uma abordagem construtivista e um tipo descritivo abrangente; o estudo permitiu conhecer e compreender as realidades das ações humanas em virtude do problema formulado. Os instrumentos de coleta de dados utilizados foram o teste de conhecimentos, o questionário do teste, uma oficina de uso e aplicação, uma oficina de avaliação, um questionário e um diário de campo aplicado aos 12 alunos da amostra. Os resultados indicam que na perspectiva heurística, o professor é o ator educacional fundamental, capaz de diagnosticar e detectar situações práticas, como protagonista da ação educativa. Em conclusão, os achados encontrados fortalecem o processo de ensino e aprendizagem de matemática para identificar as políticas e diretrizes que devem ser seguidas na Instituição de Ensino.
Palavras-chave: resolução de problemas, método, ensino, aprendizagem, construtivismo.
1. Introducción
El proyecto de investigación titulado Método Heurístico de George Pólya en la resolución de problemas matemáticos en estudiantes de grado sexto de la institución educativa (IE) San Luis Gonzaga del municipio de Túquerres es el resultado de la participación de los estudiantes de la comunidad educativa, quienes dan a conocer las falencias en cuanto a la enseñanza y el aprendizaje; una parte del problema se puede atribuir a los métodos de enseñanza tradicional que, según Gómez (2010), es seguir procedimientos rutinarios dentro del salón de clases, limitándose a tres momentos: el primero alude a la explicación de los temas a tratar por parte del docente; el segundo se basa en que los estudiantes realizan algunos ejercicios que el docente plantea de un libro de texto; y, el tercero, es desarrollar ejercicios similares a los trabajados en clase. Lo anterior genera mayor desmotivación en el estudiante frente a la materia (Calvo, 2008).
Por tanto, esta investigación cualitativa buscó, de manera comprometida, adquirir un modelo que potencialice el desarrollo de un estudiante autónomo; la necesidad de hacer posible la resolución de problemas matemáticos es una preocupación global. Pólya (citado en Echenique, 2006) afirma que el docente tiene en sus manos la llave del éxito, pues si es capaz de despertar la curiosidad en el estudiante al momento de enfrentarse a un problema, hará que éste encuentre el significado y el valor de la matemática. Según Pólya, para resolver un problema se debe tener fundamentalmente interés por resolverlo. De esta manera, la actitud que puede matar un problema es, precisamente, el desinterés; por ello, se debe buscar la manera de captar el interés del estudiante para resolver problemas. Entonces, es relevante el tiempo que se dedique a exponer el problema; el profesor debe atraer a los estudiantes hacia el problema y motivar su la curiosidad. Un método que suele resultar útil es el de la imitación; es decir, el profesor debe ser un modelo para la resolución de problemas.
De ahí que, el objetivo general de esta investigación fue determinar el aporte del método heurístico de George Pólya en la resolución de problemas matemáticos con operaciones combinadas en estudiantes de grado sexto de la Institución Educativa (IE) San Luis Gonzaga del municipio de Túquerres. Siguiendo un horizonte investigativo, se contempla el desarrollo de tres objetivos específicos, a saber: Identificar las dificultades que presentan los estudiantes de grado sexto en la resolución de problemas con operaciones combinadas, lo cual se proyectó en aquéllos que tenían ausencia de la comprensión del lenguaje natural y lenguaje matemático, motivo que los lleva a cometer errores en el diseño de esquemas mentales para solucionar el problema, Así mismo, se evidenció que los procedimientos realizados carecen de rigurosidad y de procesos de revisión, lo cual contrasta con lo que expone el Ministerio de Educación Nacional (MEN, 2006), que considera que el estudiante de grado sexto debe ser capaz de configurar estructuras conceptuales del sistema de números naturales. De igual manera, se hizo necesario justificar la elección de métodos e instrumentos de cálculo en la resolución de problemas.
El segundo objetivo consistió en aplicar y usar el método heurístico de George Pólya en la resolución de problemas matemáticos con operaciones combinadas, mediante el cual se pretendió que los estudiantes sean más analíticos y ordenados, mejorando su actitud; además, que regulen sus procesos matemáticos y que consideren el planteamiento de problemas, como una actividad práctica e interesante. Conviene subrayar que lo anterior fue fortalecido a través de clases dinámicas, por medio del juego como instrumento de aprendizaje. Así, se les permitió a los estudiantes usar y aplicar una estrategia de resolución que no únicamente los guíe para dar una respuesta inmediata y simple, sino que sea debatida y confrontada con el equipo de trabajo.
El tercer objetivo consistió en evaluar los desempeños de los estudiantes en la resolución de problemas matemáticos con operaciones combinadas, a través de la aplicación del método heurístico de George Pólya. Los estudiantes, al momento de resolver problemas matemáticos, demostraron interés y preocupación por la comprensión y resolución de los problemas; es necesario mencionar que en la presente investigación se hizo uso de la lúdica y el juego como herramientas potenciales para generar un cambio de actitud en los estudiantes, al permitir la aceptación tanto del método heurístico como la resolución de problemas, intención presente en la acepción establecida por Pólya (1965), para quien un problema significa buscar de forma consciente una acción apropiada para lograr un objetivo claramente concebido, pero no alcanzable en forma inmediata.
Finalmente, es importante destacar que las opiniones y acciones destacadas en este trabajo dan respuesta al Proyecto Educativo Institucional (PEI) propuesto por la Inatitución Educativa (IE) San Luis Gonzaga del municipio de Túquerres. Además, se tiene en cuenta las categorías y subcategorías desarrolladas junto con las categorías inductivas y deductivas que se encuentran sustentadas bajo teóricos destacados como Parodi (citado por Rosales y Salvo, 2013), Mamani y Villalta (2017), Monereo, Castelló, Clariana, Palma y Pérez (1999), Pólya (citado por Aguilar, 2014), quienes consideran que, al terminar de solucionar un problema, es necesario revisar el desarrollo que se le ha dado, identificando si es correcta o no la forma como ha buscado llegar a la meta y reflexionando si se podría llegar de otra forma; por lo tanto, el proceso de resolución de problemas es un intento de encontrar la relación que existe entre una situación problémica con otra, llevando a los estudiantes a una comprensión estructural.
2. Metodología
La importancia de la metodología radica en la participación de los sujetos y objetos investigados al mismo tiempo, ya que el propósito de esta investigación consistió en comprender el fenómeno social: Método heurístico de George Pólya en la resolución de problemas matemáticos en estudiantes de grado sexto, lo cual involucra a las personas (sujetos) dentro de un contexto educativo que requiere tenerse en cuenta en el estudio descriptivo-comprensivo para la obtención de la información de datos y su correspondiente análisis.
Paradigma, enfoque y tipo de investigación
Paradigma de investigación. La presente investigación se realizó desde un paradigma cualitativo naturalista, ya que se buscó describir, comprender e interpretar los fenómenos, explorándolos desde el sentido y significado que dan los participantes en un ambiente natural y en relación con su contexto (Hernández, Fernández y Baptista, 2014). Por su parte, Guardián (citado por Derazo y Riascos, 2018) considera que este tipo de investigación “está orientada al descubrimiento de categorías y patrones que se obtiene mediante la observación y la descripción” (p. 57).
Enfoque. La investigación se desarrolló bajo el enfoque constructivista, pues permite conocer y comprender algunas realidades de las acciones humanas en cuanto a la problemática planteada, en particular de un grupo de estudiantes de grado sexto. A partir de ahí, se propuso estrategias que posibilitaron obtener mejoras en cuanto a la resolución de problemas y dominio de estrategias pedagógicas, mas no necesariamente, se buscó generar transformaciones en cuanto a la práctica pedagógica. Al realizar el estudio de las acciones humanas sin fragmentarlas, tomándolas enteras, es decir, en su totalidad, en su conjunto, convirtió el enfoque en holístico. Así mismo, fue un enfoque inductivo, pues se construye categorías e interpretaciones a partir del lugar de estudio y no con base en teorías previas (Derazo y Riascos, 2018); finalmente, se buscó comprender e interpretar lo singular de los fenómenos sociales (Latorre, Rincón y Arnal, 2003).
Tipo de investigación. Con base en los objetivos propuestos, el estudio fue de tipo investigación–acción, ya que se buscó propiciar un cambio social, transformando la realidad educativa (Sádin, citado por Hernández et al., 2014). Este tipo de investigación se centra en tres momentos clave: el observar, el pensar y el actuar, los cuales se dan de manera cíclica.
Inicialmente, se interpretó y comprendió los conocimientos y procedimientos que los estudiantes ponen en juego al momento de resolver problemas con operaciones combinadas. A continuación, buscando mejoras en los procesos que los estudiantes utilizan al momento de resolver problemas, se les enseñó el método heurístico de George Pólya; finalmente, se realizó una evaluación del uso y significado que le dan al método en mención al trabajar con problemas.
Modelo y diseño de la investigación
El método heurístico de George Pólya en la resolución de problemas matemáticos con operaciones combinadas en estudiantes de grado sexto de la IE San Luis Gonzaga del municipio de Túquerres está representado en la Figura 1:
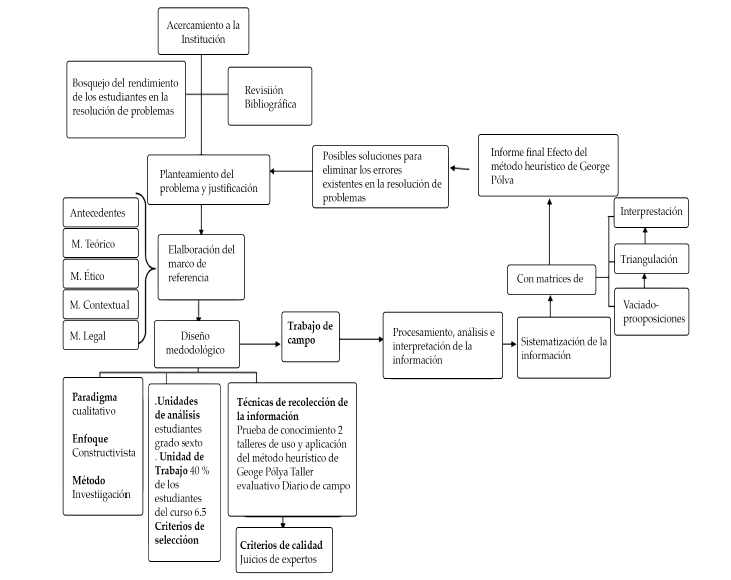
Línea de investigación. Formación y Práctica Pedagógica:
Integra en su reflexión al investigador como un “sujeto pensante” que frente a la misión institucional y del programa asume su postura de pensador reflexivo con sensibilidad humana, cognitivo y con habilidades sociales para trabajar en red y en colectivo, permitiendo una formación humano cristiana social, que profundice en el concepto de persona como soporte esencial del desarrollo humano, se fundamente conceptualmente para el análisis de la problemática educativa nacional, internacional y latinoamericana, efectuando un análisis de la problemática y el conocimiento educativo desde las ciencias de la educación y pedagogía, y asuma el currículo como un proceso de investigación que vincule las áreas temáticas y la línea de investigación en su contenido curricular. (Universidad Mariana, s.f., p. 2).
Área de investigación
Didáctica disciplinar y mediática. Este eje o núcleo problémico permite abordar el segundo y el tercer nivel de la pedagogía, la intermediación y la aplicación, desarrollando los procesos de enseñanza y aprendizaje, mediante una estrecha vinculación con las estrategias de enseñanza, aprendizaje y evaluación. Sus líneas de trabajo son las estrategias de enseñanza, estrategias de aprendizaje y evaluación para metodologías. (Universidad Mariana, s.f., p. 5).
3. Resultados
Se realizó aplicación de matrices de vaciado de información, reducción del dato, triangulación, categorías inductivas, matriz de interpretación y recursos de análisis, a través de taxonomías.
Objetivo específico 1. Identificar las dificultades que presentan los estudiantes de grado sexto en la resolución de problemas con operaciones combinadas.
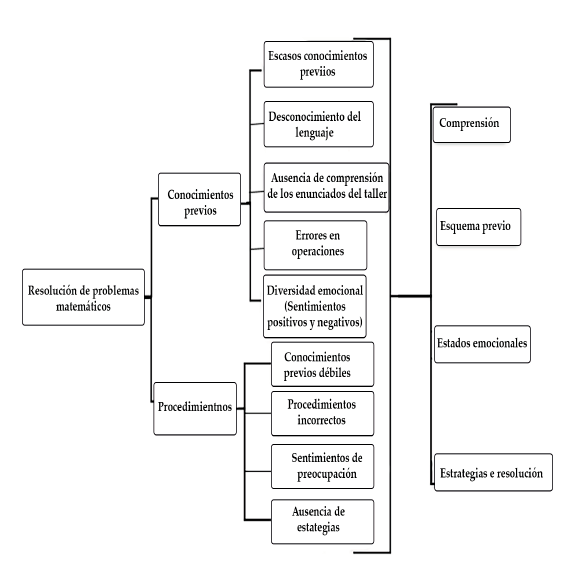
Códigos taxonomía 1.
Categoría deductiva: Resolución de problemas matemáticos.
Subcategorías: Conocimientos previos, procedimientos.
Categorías inductivas: Comprensión, esquema previo, estados emocionales, estrategias de resolución.
Código de los participantes. Estudiantes: S1: sujeto 1; S2: sujeto 2; S3: sujeto 3; S4: sujeto 4; S5: sujeto 5; S6: sujeto 6; S7: sujeto 7; S8: sujeto 8; S9: sujeto 9; S10: sujeto 10; S11: sujeto 11; S12: sujeto 12.
Códigos de talleres y procedimientos:
T1P1S1: taller 1, problema 1, sujeto 1.
T1P1S2: taller 1, problema 1, sujeto 1.
T1P2S2: taller 1, problema 2, sujeto 2.
T1P2S5: taller 1, problema 2, sujeto 5.
T1P2S9: taller 1, problema 2, sujeto 9.
T1P2S10: taller 1, problema 2, sujeto 10.
T1P2S11: taller 1, problema 2, sujeto 11.
T1P3S8: taller 1, problema 3, sujeto 8.
T1P3S2: taller 1, problema 3, sujeto 2.
Categoría: Resolución de problemas matemáticos
En esta categoría se analizó los procesos desarrollados por los estudiantes al momento de aplicar la prueba de conocimiento de problemas con operaciones combinadas, donde se identificó las dificultades que presentan.
Al identificar dichas dificultades, la aplicación del resultado de la prueba de conocimiento proyectó que los estudiantes presentan una ausencia de comprensión de lenguaje natural y lenguaje matemático, lo cual los lleva a cometer errores en el diseño de esquemas mentales para solucionar el problema. Así mismo, se evidenció que los procedimientos realizados por los estudiantes carecen de rigurosidad y de procesos de revisión. Lo anterior contrasta con el MEN (2006), quien considera que el estudiante de grado sexto debe ser capaz de configurar estructuras conceptuales del sistema de números naturales. Así mismo, debe justificar la elección de métodos e instrumentos de cálculo en la resolución de problemas. De manera análoga, los Derechos Básicos de Aprendizaje (DBA) del MEN (s.f.) explicitan que en este grado escolar se debe ser capaz de interpretar números naturales con sus operaciones en diversos contextos.
En resumen, lo evidenciado en la prueba de conocimientos permite afirmar que no se está cumpliendo con supervisiones institucionales y prescripciones legales, donde los factores que han llevado al no cumplimiento de estos lineamientos son: el poco dominio de conocimientos previos, el desinterés por parte del estudiante, el desconocimiento de estrategias que lo ayuden a resolver problemas, entre otros. Así pues, al trabajar la resolución de problemas en grado sexto, se está aportando y trabajando con lo establecido en supervisiones institucionales.
Subcategoría conocimientos previos. Con relación a esta subcategoría, se pretende identificar la comprensión de problemas, la extracción de datos, así como el análisis de los mismos. Silva, Rodríguez y Santillán (s.f.) consideran que los conocimientos previos son una parte fundamental para la adquisición del nuevo conocimiento, pues el sujeto construye los conocimientos en función de sus experiencias, creencias e ideas previas. Así pues, es fundamental la identificación de los mismos para saber las facultades y dificultades que presentan los estudiantes con relación a estos.
Los resultados demostraron que, independientemente del problema que se trabaje, los estudiantes no entendían qué significaba describir el problema en sus propias palabras, demostrando una ausencia de comprensión de este enunciado, ya que solo uno de los doce estudiantes lo realizó; sin embargo, éste dejó de lado lo que se tenía que buscar para solucionar el problema, tal como se evidencia a continuación:
T1P1S1: “Que Pedro entra a una tienda de ropa y que compra tres pantalones a 72.000 cada uno y dos camisetas a 15.000 la unidad”.
Lo realizado por T1P1S1, demuestra que el S1 describe en sus palabras la información del problema, pero al no tener en cuenta la pregunta, su esfuerzo de describir el problema es poco interesante.
Los once estudiantes restantes demostraron que, para ellos, describir el problema consistía en la generación de un plan para resolverlo o en la realización de operaciones; otros optaron por dejar el espacio en blanco. Un ejemplo es lo realizado por el S2, el S9 y el S10; el primero diseña, mas no describe; el segundo menciona qué operación debe desarrollar y el tercero afirma no entender el problema, como se evidencia a continuación:
T1P1S2: Yo lo que entiendo es que para desarrollar la primera pregunta, toca multiplicar 72.000 por 3 y así sacamos la primera pregunta; para sacar el valor de las camisetas debe multiplicar 15.000 por 2 y así sacamos la segunda respuesta; para sacar el valor de lo que Pedro gasta en la tienda debe sumar el primer valor de la primera pregunta más el valor de la segunda pregunta y así sacamos el valor de la tercera pregunta; y la cuarta pregunta, se debe que restar el valor de la tercera pregunta menos 300.000 que tenía y así se saca la cuarta pregunta”.
T1P2S9: “6 litros = 100 kilómetros; 57 litros 750 km. Entonces, tengo que dividir 750 entre 57”.
T1P2S10: “No lo entendí”.
Los testimonios y procedimientos de la prueba y el cuestionario demostraron que la mayoría de los estudiantes no comprenden los enunciados del problema ni mucho menos, pueden interpretar los datos ya que, de 72 respuestas, 49 son incorrectas, errores que se da, en su mayoría, por la no comprensión de los problemas, los errores en los procesos aritméticos y, más aún, al desconocimiento de métodos o estrategias que los ayuden a encontrar la solución de un problema.
Lo anterior permite vislumbrar el poco y casi nulo conocimiento de estrategias de resolución de problemas pues, al buscar dar solución a un problema y no saber cómo iniciar el proceso de resolución y mucho menos qué pasos seguir para llegar a la meta, los estudiantes prefieren dejar el espacio en blanco antes de crear un esquema mental para solucionarlo.
Considerando los testimonios únicamente para el segundo problema de la prueba, tres de los doce estudiantes -T1P2S5, T1P2S10, T1P2S11- no efectuaron ningún procedimiento y el S11 consideró que no lo entiende por desconocimiento del término ‘tanquear’; de igual forma, el S12 afirmó: “No sé cómo lo hice, porque casi no entiendo”, dejando claro que en ocasiones se opera sin razonamiento.
Sin embargo, al responder el cuestionario de la prueba, algunos consideraron que, al momento de desarrollar los problemas, aplicaron los conocimientos adquiridos con anterioridad, lo cual los hizo sentir bien. Como muestra de esto, S3 expresó que “fue una experiencia buena, porque los conocimientos que ya conocíamos los pudimos ejercitar y no olvidarlos fácilmente” y S5 afirmó: “estos problemas son excelentes, porque nos hacen ver la capacitación que tenemos para desarrollarlos”
No obstante, también se apreció emociones negativas con mayor frecuencia, tal como se presenta en los siguientes testimonios:
S7: “Me sentí un poco incómoda y un poco nerviosa”
S8: “Algunos problemas no los pude hacer”
S9: “Un poco bien, porque no los entendí casi todos”.
Al respecto, Gómez (2010) razona que las falencias que presentan los estudiantes al desarrollar un problema, surgen debido al desconocimiento de estrategias de resolución de problemas, a la poca motivación por parte del docente hacia ellos para acércalos a la resolución de problemas y a la enseñanza tradicional, la cual se basa solo en ejercicios.
Subcategoría procedimientos. En esta subcategoría se analizó los procedimientos realizados por los estudiantes de grado sexto al momento de desarrollar los problemas. Se identificó errores en cuanto al dominio de las cuatro operaciones básicas. Los resultados permitieron identificar que la suma es la operación que mejor dominan los estudiantes; en lo referente a la resta, multiplicación y división, la mayoría presentaron errores; por ejemplo, en el desarrollo del problema 1, el S2 interpretó el problema correctamente y diseñó un plan adecuado para resolverlo, pero cometió un error al momento de realizar la resta; según S2, 270.000 menos 216.000 da como resultado 154.000
Lo anterior es un claro ejemplo que señala que los procedimientos incorrectos surgen debido a la poca revisión, a la no comprensión de los problemas o al poco dominio de las operaciones básicas. En el caso del proceso realizado por el S9, al desarrollar el problema 2, identificó errores en la descripción del problema, ya que elaboró un plan general e incorrecto, mencionando que el problema se solucionaba realizando unas multiplicaciones; además, realizó una división, ya que dividió 750 entre 57 y consideró que era una división exacta y que el resultado era 10.
De manera análoga, los resultados de la investigación permitieron conocer que los estudiantes tienden a confundirse y equivocarse más en problemas cuya solución necesita hacer uso de diversas operaciones. Los resultados desmejoran si los problemas presentan los datos sin un orden establecido, como lo considera Echenique (2006): este tipo de problemas lleva al estudiante a generar esquemas conceptuales más elevados para su solución, pues requieren organizar los datos y realizar operaciones pertenecientes a diferentes campos conceptuales; sin embargo, cuando se presenta al estudiante herramientas para enfrentarse a este tipo de problemas, afirma que el grado de complejidad del problema le reforzará sus estructuras conceptuales, las cuales, según Novack (citado por Silva et al., s.f.), son las encargadas de articular los conocimientos previos con los nuevos conocimientos.
En el desarrollo del cuestionario de la prueba de conocimiento de problemas con operaciones combinadas, los sujetos S6 y S7 afirmaron que una de las dificultades que se les presentó fue el trabajar con problemas cuya solución necesitaba más de una operación. Por ejemplo, S7 dijo: “se me dificultó un poco las combinaciones, pero haciendo las operaciones que yo pensaba que eran correctas ya se me iba dando el resultado bien”.
A continuación, se define las categorías inductivas obtenidas en el primer objetivo específico, las cuales son: comprensión, esquema previo, estrategias de resolución y estados emocionales. Para cada categoria inductiva se identificó caracteristicas o causales que las generan, buscando tener una base sólida para su corrección, las cuales surgieron de los resultados obtenidos de las subcategorías Conocimientos previos y Procedimientos, que se presenta resumidos en la Figura 2. Ruckert (citado por Derazo y Riascos, 2018) considera que “un error despejado proporciona una sólida base” (p. 91). Asi, dichas características despejadas pueden convertirse en un punto de partida para generar un aprendizaje significativo a traves del metodo heurístico de George Pólya. Enseguida se describe cada categoria inductiva junto a las causas que las generan.
Categoría inductiva: Comprensión
Al buscar la solución a los problemas con operaciones combinadas, se pudo identificar en los estudiantes diversos aspectos; entre estos, que no tienen bien fundamentados sus conocimientos previos, tanto al momento de comprender el problema, mostrando su grado de abstracción con el mismo, como al momento de desarrollar procedimientos, pues se evidenció fallas en el desarrollo de las diversas operaciones. Para comprender mejor esto, se considera el siguiente testimonio:
T1P2S2: “Yo lo que entiendo es que 750 km se gasta 35 litros de gasolina, porque si en 100 se gasta seis litros, entonces en 700 se gasta 32 litros y en 750 se gasta 35 litros, porque 7 x 6 = 32; entonces, la mitad de 6 es tres y la mitad de 100 es 50; por eso lo entiendo”.
Lo desarrollado por el S2 y descrito anteriormente, permite identificar que no comprende la solicitud de la prueba, pues se le solicitó que describiera el problema en sus propias palabras, mas no que diseñara un plan para desarrollarlo. Por otra parte, está cometiendo errores en procedimientos debido a la debilidad en sus conocimientos previos, pues, según él, 7 x 6 es igual a 32.
Con relación a ello, Parodi (citado por Rosales y Salvo, 2013) considera que la comprensión es el proceso que permite elaborar el significado de un texto con las ideas que ya se tiene. Así, la comprensión de los estudiantes es débil, tal como se evidenció en los testimonios considerados para el análisis de resultados de las subcategorías Conocimientos previos y Procedimientos, pues no saben leer comprensivamente ni tienen las herramientas disciplinares para resolver los problemas matemáticos; o, saben comprender, pero no tienen los conocimientos necesarios para resolver los problemas; por lo tanto, surge la necesidad de que los docentes generen estrategias que ayuden a los estudiantes a mejorar su proceso de comprensión. Además, según los Derechos Básicos de Aprendizaje -DBA-, es más que necesario que el estudiante sea capaz de comprender e interpretar contenidos matemáticos en diversos contextos al resolver problemas. En este punto, se presenta las causas que generaron esta categoría inductiva, agrupadas en: Desconocimiento de lenguaje y Entendimiento.
Desconocimiento de lenguaje. El desconocimiento del lenguaje abarcó las dificultades que presentaron los estudiantes al comprender los enunciados, tanto de la prueba de conocimiento como de los problemas de la misma. Por ejemplo, T1P3S8, para desarrollar el problema 3, afirmó lo siguiente: “El 225.000 se lo multiplica por 25 y ahí da el resultado para saber cuánto costaron las boletas”.
Lo realizado por el estudiante S8 evidenció el desconocimiento del lenguaje, pues inicialmente no relaciona los datos con la pregunta, ya que busca el valor total de las boletas, dato que el problema había dado. En cuanto al lenguaje matemático, la expresión ‘cada uno’ se relaciona con el repartir, aludiendo a una división y no a una multiplicación.
Por otra parte, si se trabaja con problemas cuyo contexto es desconocido por el estudiante, se convierte en algo más complicado para el mismo. Por ejemplo, el S11, al desarrollar el problema 2, sostuvo: “Un poco lo entiendo, porque la pregunta es difícil; no entiendo la palabra tanquear, bueno”. Este testimonio demuestra que se le dificultó comprender el problema por desconocimiento del contexto.
Finalmente, en la prueba de conocimiento se les solicitó a los estudiantes que escribieran el problema con sus propias palabras; solo uno de los doce estudiantes comprendió la solicitud, aun cuando no la realizó adecuadamente; los demás realizaron procesos que evidenciaron la escasa comprensión a la misma, demostrando así que tienen poca comprensión de instrucciones textuales y del enunciado de los problemas.
Entendimiento. Alude a las falencias que presentaron los estudiantes al resolver problemas, las cuales surgen debido a que no entienden el enunciado ni encuentran conocimientos previos, situaciones, vivencias o experiencias que los ayuden a enfrentarse al problema.
Como fundamentación de lo dicho, están los sujetos que prefieren dejar el espacio en blanco, sin realizar operaciones o descripciones al problema, antes de aventurarse a diseñar un plan para resolverlo.
Barrera-Mora y Reyes-Rodríguez (2017) consideran que el entendimiento es una parte esencial que debe realizar el estudiante al enfrentarse a problemas matemáticos, pues al entender un concepto, una situación o un problema, le permite afianzar sus conocimientos previos y, a la vez, estos le sirven como base para adquirir nuevos conocimientos. El entendimiento es “una idea compleja, en constante cambio y crecimiento […]; entender algo significa determinar cómo ese algo se conecta y estructura con otros conocimientos al abordar y resolver problemas” (p. 111).
El no entendimiento genera en ellos sentimientos negativos que los alejan de la resolución de problemas; además, al no saber cómo actuar ante un determinado problema, prefieren dejarlo de lado y perder la oportunidad de incrementar su desarrollo cognitivo, razón por la cual, se busca dar una solución a la debilidad de comprensión que presentan los estudiantes, a través del método heurístico de George Pólya, el cual genera habilidades de comprensión de un párrafo, al extraer inferencias del mismo. En sí, les lleva a tener dominio de la comprensión lectora y la resolución de problemas, que son capacidades básicas que el estudiante necesita desarrollar para lograr diversos aprendizajes (Rosales y Salvo, 2013).
Categoría inductiva: Esquema previo
Las dificultades que presentan los estudiantes al momento de resolver problemas con operaciones combinadas surgen, en la mayoría de los casos, por falta de dominio en los conocimientos previos que deben poseer. Por ende, es necesario apropiarse de la importancia de los conocimientos previos, como ese puente que articula las experiencias, las creencias o ideas que han adquirido con los nuevos conocimientos que se les presentan (Silva et al., s.f.).
Esta categoría, con base en los resultados obtenidos en la prueba de conocimiento, surgió por el mínimo aprendizaje que adquirieron los estudiantes.
Mínimo aprendizaje. Se encuentra conformado por las dificultades que presentan los estudiantes al momento de enfrentarse a problemas con operaciones combinadas. Estos problemas surgen debido al aprendizaje poco significante que han tenido, lo cual puede deberse a varios factores, como: la enseñanza tradicional en la cual, según Calvo (2008), el profesor de matemáticas solo utiliza ejercicios y no considera los problemas en el desarrollo de sus clases; otro problema es la ausencia de estrategias de motivación, ya que el docente dicta su clase, pero deja a la lúdica y al juego fuera de ella. De esta manera, la ausencia de estrategias para la resolución de problemas se convierte en otro aspecto fundamental cuando el estudiante se enfrenta a los problemas, pues su desconocimiento hace que no sepa cómo actuar ante los mismos.
Lo anterior demostró que es fundamental que usar métodos o mecanismos que ayuden, por una parte, a mejorar los conocimientos previos y, por otra, que el dominio de los mismos permita al estudiante comprender, crear, argumentar y solucionar cualquier tipo de problemas (MEN, 2006). Es así como se plantea el método heurístico de George Pólya, como esa alternativa capaz de crear habilidades en los estudiantes, que los lleve, en palabras de Rosa (citado en Mamani y Villalta, 2017), a utilizar y ejercitar de modo estratégico sus conocimientos o procedimientos previamente conocidos.
Categoría inductiva: Estrategias de resolución
Se considera por estrategia, los procesos necesarios para encontrar la solución de un problema, dado que permiten comprender e interpretar el problema. Además, llevan al estudiante a que haga uso de los conocimientos que posee, para poder plantear y ejecutar un plan que desarrolle el problema, llegando a la solución del mismo (Monereo et al., 1999). Los procesos y acciones realizados por los estudiantes evidenciaron una ausencia de estrategias de resolución de problemas, pues inicialmente no existe una comprensión clara del lenguaje natural ni del planteamiento de los problemas, como tampoco existe una idea de cómo realizar un plan para resolver un problema y cuando existe, el estudiante no justifica el porqué. Una vez el estudiante considera que ha llegado a la solución de los problemas, deja de lado la fase de evaluación de lo que ha desarrollado, donde el fin es encontrar decisiones, operaciones mal desarrolladas o darle validez a su proceso.
Dicho esto, es claro que la ausencia de estrategias de resolución de problemas es una dificultad que presentan los estudiantes de grado sexto, la cual puede darse por múltiples factores. Acorde con los resultados descritos, es evidente que carecen del dominio del método heurístico, pues existe una ausencia de facultades y aptitudes al momento de resolver los problemas.
Para que los estudiantes empiecen a tener mejoras en la resolución de problemas, es urgente que se les presente estrategias y heurísticas que sean guías, pistas y procedimientos que los orienten en dicho proceso.
Categoría inductiva: Estados emocionales
Trabajar con problemas de operaciones combinadas lleva al estudiante a vivir diferentes sentimientos, ya sean buenos o malos; por ejemplo, no entender un problema en su totalidad produce frustración, angustia y preocupación, pues no sabe cómo desarrollar el problema y las cosas empeoran si no conoce estrategias que le ayuden a solucionarlo. Esto hace que sus estados emocionales se vean alterados, estados que son considerados como “respuestas afectivas caracterizadas por una alta intensidad y activación fisiológica que experimentan los alumnos, y que surgen en respuesta a una tarea matemática que tiene una carga de significado positiva o negativa para ellos” McLeod (citado por Díaz, Belmar y Poblete, 2018, p. 1.203). Así, al hablar de estados emocionales, se considera, en palabras de Guerrero y Blanco (2004), las actitudes hacia la matemática, lo que alude a la valoración, aprecio e interés por la materia y por su aprendizaje.
Lo desarrollado por los estudiantes en la prueba de conocimiento y lo escrito en el cuestionario demostró que éstos experimentaron emociones, en su mayoría, negativas; por ejemplo, se les preguntó si se les presentó alguna dificultad, ante lo cual, tres de los doce estudiantes respondieron que no y el resto mencionó diversas dificultades, como el S11: su “dificultad fueron las preguntas de los problemas”. En este sentido, Gómez (2010) cree que estas emociones negativas son generadas por el escaso conocimiento y uso de estrategias, así como por sus débiles conocimientos previos, demostrando que situaciones como estas los llevan a crear barreras contra la resolución de problemas y, a la vez, contra la asignatura.
La categoría inductiva Estados emocionales surgió por los sentimientos positivos y negativos que se evidenció en los estudiantes, al desarrollar la prueba de conocimiento de operaciones combinadas, las cuales se describe a continuación.
Sentimientos positivos. Surgen cuando los problemas despiertan en el estudiante la curiosidad, la cual los lleva a intentar dar una solución al problema para sentir un grado de satisfacción considerablemente bueno. Es necesario mencionar que fueron muy pocos los estudiantes que afirmaron tener sentimientos positivos al desarrollar la prueba, pues solo tres de los doce expresaron que no tuvieron dificultades; además, en sus comentarios manifestaron que la prueba les permitió ejercitar sus conocimientos previos. Por consiguiente, es necesario presentar la resolución de problemas mediante clases lúdicas que motiven al estudiante y que despierten su curiosidad. Con base en esto, Ruiz (2017) plantea que el docente es importante en este proceso, pues es el facilitador del conocimiento y el punto clave del proceso de enseñanza-aprendizaje, generándolo de manera llamativa, creativa, independiente y, sobre todo, responsable, en cuanto a las situaciones de la vida, demostrándole que la resolución de problemas es un proceso que articula los contenidos matemáticos desde las realidades humanas, haciéndolos más entendibles, prácticos y útiles, generando ese grado de satisfacción y despertando el interés y gusto por la resolución de problemas y por las matemáticas.
Sentimientos negativos. Los estudiantes llegaron a sentir frustración, angustia y enojo consigo mismos, al enfrentarse a problemas de operaciones combinadas, sentimientos que pueden surgir por:
* Enseñanza tradicional. Pues solamente han trabajado con ejercicios y el docente no ha presentado problemas y mucho menos estrategias para dar soluciones, tal como se evidencia en lo realizado por los estudiantes en el desarrollo de la prueba de operaciones combinadas, donde no utilizaron estrategias heurísticas para dar solución.
* Ausencia de estrategias. Estrategias de motivación por parte del docente, quien es el encargado de aumentar la fe en el estudiante, sobre su propia habilidad matemática. Además, es el encargado de presentar estrategias que sean guías u orientaciones, para que el estudiante las pueda utilizar al momento de enfrentarse a cualquier tipo de problemas.
Los resultados del objetivo específico uno, presentados en categorías y subcategorías deductivas e interpretados en categorías inductivas, evidenciaron las falencias que presentaban los estudiantes en cuanto a la resolución de problemas, demostrando la necesidad de implementar el método heurístico de George Pólya como facilitador de conocimiento, además de una guía orientadora que genere autonomía y despierte el sentido crítico del estudiante.
Lo dicho evidencia la necesidad que tienen los estudiantes de aplicar y usar el método heurístico de George Pólya, capaz de potencializar las creencias que tienen sobre sí mismos, sobre la materia y sobre los problemas. El dominio y uso de este método heurístico les dará tranquilidad y confianza para afrontar cualquier tipo de problema.
Objetivo específico 2. Aplicar y usar el método heurístico de George Pólya en la resolución de problemas matemáticos con operaciones combinadas.
A continuación, se presenta los resultados obtenidos de la ejecución del objetivo específico 2, donde se aplicó y usó el método heurístico de George Pólya en la resolución de problemas matemáticos con operaciones combinadas. Dichos resultados son resumidos en la Figura 2, donde se evidencia un avance en los estudiantes al momento de resolver un problema, gracias al conocimiento y uso del método mencionado. En efecto, el método ha logrado que los estudiantes sean analíticos y ordenados, mejoren su actitud, regulen sus procesos matemáticos y asuman el planteamiento de problemas como una actividad práctica e interesante. Conviene subrayar que lo anterior fue fortalecido a través de clases dinámicas y el juego como medio de aprendizaje, donde los estudiantes iban adquiriendo el dominio del método de manera colaborativa con sus compañeros.
A partir del análisis de las subcategorías: Comprender el problema, Diseñar un plan, Ejecutar el plan y Mirar hacia atrás, se pudo extraer las categorías inductivas: Interpretación, Planteamiento y Revisión. Los resultados de la investigación son presentados por subcategorías deductivas y categorías inductivas.
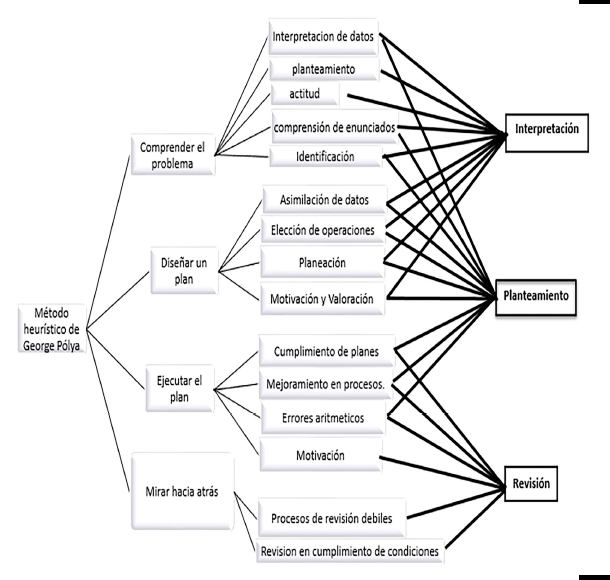
Códigos taxonomía 2:
Categoría deductiva: Método heurístico de George Polya.
Subcategorías: Comprender el problema, diseñar un plan, ejecutar el plan, mirar hacia atrás.
Categorías inductivas: Interpretación, Planteamiento, Revisión.
Códigos de la realización de talleres:
T2P1P4G1: taller 2, problema 1, pregunta 4, grupo 1.
T2P4P4G1: taller 2, problema 4, pregunta 4, grupo 1.
T2P4P4G2: taller 2, problema 4, pregunta 4, grupo 1.
T3G6: taller 3, grupo 6.
T2P1G1: taller 2, problema 1, grupo 1.
Subcategoría: Comprender el problema. En esta subcategoría se analizó los procesos que desarrollaban los estudiantes al momento inicial de la resolución de un problema con la ayuda del método heurístico de George Pólya, entre estos, la identificación, interpretación y extracción de los datos, la descripción del dato que se debe encontrar para solucionar el problema, la elección correcta del proceso inicial y la descripción del mismo.
En cuanto a la identificación, interpretación y extracción de los datos, la mayoría de estudiantes mejoró, a medida que fue adquiriendo dominio del método heurístico de George Pólya; por ejemplo, al trabajar el taller de aplicación, los resultados tuvieron un gran avance en comparación con la prueba de conocimiento de problemas con operaciones combinadas. El taller 2 de uso del método se desarrolló en tres grupos, cada uno con cuatro estudiantes; en el desarrollo de cada problema, por lo menos dos de los tres grupos interpretaron y extrajeron adecuadamente los datos.
En el vaciado del taller 3 de aplicación del método heurístico de George Pólya en la resolución de problemas matemáticos de operaciones combinadas, se evidenció el avance en cuanto a la comprensión del problema y, en particular, en la identificación, interpretación y extracción de los datos. Los estudiantes demostraron un avance significativo pues, en su mayoría, supieron extraer datos adecuadamente y adquirieron dominio al momento de identificar los datos necesarios para resolver un problema.
La comprensión de los estudiantes, al momento de enfrentarse a un problema de operaciones combinadas, mejoró considerablemente, ya que empezaron a analizar los datos de un problema, comprendiendo cuál era su función para desarrollar el problema o si no eran útiles para tal proceso; por ejemplo, en el problema Pedro compró 23 estampillas para llenar su álbum, el cual se llena con 130 estampillas. Su mamá le regala 25 estampillas para el álbum y $500 para que la próxima semana compre más estampillas. Al finalizar esta semana, ¿cuántas estampillas le faltan para completar su álbum?, se les solicitó que eliminaran el dato que sobraba. En los resultados, los seis grupos lograron identificar el dato sobrante, lo cual evidenció el nivel de comprensión que adquirieron.
Por otra parte, en el desarrollo del taller de aplicación del método heurístico de George Pólya, se les solicitó a los estudiantes diseñar problemas que cumplieran condiciones; fue el caso del problema 6, donde se les solicitó que diseñaran un problema cuya solución requiriera hacer uso de tres operaciones, dándoles la libertad de elegir la temática o contexto del problema. La respuesta demostró que la mayoría de ellos diseñó problemas correctos que cumplían con las condiciones y cuya temática aludía a sus temas favoritos o del contexto. Por el contrario, cuando se les planteó las condiciones del contexto, el cual no era tan conocido por los estudiantes, se los limitó; es el caso del problema 5, donde se les dio los datos que debían llevar el problema y el contexto del mismo. Los problemas planteados por los estudiantes demostraron que estos olvidaron algún dato, relacionaron los datos de forma incorrecta o plantearon problemas incorrectos.
Lo dicho evidenció que, para despertar la comprensión de los estudiantes, es necesario, primero, llevarlos a interpretar los datos, pues la interpretación es el primer escalón que deben subir para llegar a la comprensión; posteriormente, es necesario generar espacios donde puedan crear e imaginar las matemáticas en su contexto; esto los ayudará a ser autónomos, pensar lógicamente, mirar a las matemáticas en su diario vivir y adoptar una actitud positiva en cuanto a la resolución de problemas y, a la vez, en las matemáticas.
En lo referente a la comprensión sobre cuál era el dato o los datos que debían encontrar para solucionar el problema, y cómo empezar a solucionarlo, los estudiantes se expresaron con respuestas claras y acertadas y consideraron que la identificación de estos dos datos les ayudó a entender más el problema y a pensar cómo lo iban a desarrollar.
En cuanto a la descripción del problema, se identificó que los estudiantes empezaron a describir los problemas asertivamente, pues dejaron de considerar que la descripción de éste consistía en diseñar un plan para resolverlo, tal como lo hicieron en la prueba de conocimiento de problemas con operaciones combinadas. Por ejemplo, en el taller 2 de uso del método heurístico de George Pólya, describieron correctamente los problemas, con pequeños errores, pero se identificó que mejoraron al momento de comprender tanto el lenguaje natural de la tarea como el lenguaje natural y matemático de los problemas.
En las tres sesiones del desarrollo de los talleres de aplicación y uso del método heurístico de George Pólya, se evidenció que la actitud de los estudiantes iba mejorando al enfrentarse a la resolución de los problemas, pues estos consideraron al método heurístico de George Pólya como un método estratégico, cuya intención era desarrollarlo paso a paso. Aseveraron que les daba mucho gusto trabajar con problemas diferentes, extraer datos y crear sus propios problemas con temas de su agrado, pero cumpliendo condiciones. En definitiva, el método heurístico de George Pólya les ayudó considerablemente, tanto a nivel actitudinal como a nivel conceptual, por cuanto desarrollaron los problemas con mayor alegría y entusiasmo, además de mejorar su comprensión.
Subcategoría: Diseñar un plan. En el desarrollo de esta subcategoría se tuvo en cuenta cómo los estudiantes diseñaban planes para resolver problemas, las operaciones que iban a utilizar, el orden en que las necesitaban y cuál era la función de los datos al desarrollar el problema.
Inicialmente, en esta subcategoría en el desarrollo de los talleres de uso y aplicación del método heurístico de George Pólya, los estudiantes presentaron respuestas que evidenciaron la comprensión a los problemas, al identificar qué pedía el problema y cómo utilizar los datos de cada problema, los cuales debían dar respuesta al mismo; es decir, fueron conscientes de lo que podían obtener con los datos.
En lo referente a la elección de operaciones, los estudiantes eligieron las correctas; en cuanto al diseño del plan, en la mayoría de los problemas, elaboraron planes adecuados para desarrollarlos.
T2P4P4G1: “Primero, a 20 le sumamos 15, que son las personas que subirán y nos da un resultado de 35 y luego a 35 se resta 13, que son las personas que se han bajado y nos da un resultado de 22, o multiplico por 6, que son los autobuses de la segunda parada”.
Algunos estudiantes fueron describiendo y desarrollando los problemas en el segundo paso del método heurístico de George Pólya; por ejemplo, T2P1P4G1 realizó lo siguiente:
T2P1P4G1: “Primero, a 200 lo dividimos por 4, nos da el resultado de 50 estampillas; luego, a 200 le restamos las 50 estampillas; a 150 lo dividimos entre 2; nos da un resultado de 75; a 150 le resto 75; luego a 75 lo divido entre 5; me da un resultado de 15 estampillas y a 75 – 15 = 60 y esas 60 estampillas son las que le sobran a Paula”.
Al desarrollar el segundo paso del método heurístico de George Pólya, los estudiantes efectuaron una asimilación de los datos, como pautas o pistas para comprender, interpretar y desarrollar los problemas. Por otra parte, dieron comienzo a trabajar mentalmente y conocer las operaciones que debían utilizar para desarrollar los problemas, pues en la mayoría de sus respuestas, mencionaron las operaciones correctas para solucionar los problemas.
La mayoría de estudiantes tuvo una evolución notoria al momento de generar planes para desarrollar los problemas, dado que seleccionaron los datos correctos, utilizaron las operaciones y orden adecuados para diseñar dichos planes, como se evidencia en este testimonio: T2P4P4G2: “Primero, a las 20 personas les voy a sumar 15 y le vamos a restar las 13 personas; después, al resultado lo multiplico por los 7 autobuses”.
Finalmente se evidenció que, en el desarrollo de esta subcategoría, los estudiantes al trabajar en grupo realizaron un trabajo cooperativo, reflexionando sobre los procesos que debían desarrollar para llegar a la solución de los problemas. Además, en los cuestionaros, informaron que sintieron motivación al diseñar planes para resolver los problemas y valoraron la importancia de los mismos, como se evidencia en algunos argumentos:
S8: “Me gustó que es como una ruta, cuando hacemos el paso 2; pensamos en lo que toca hacer y eso es bueno para responder los problemas”.
S12: “En mi caso, el cuarto paso casi no lo hacía, pero cuando trabajamos y lo hicimos el cuarto paso, sí nos sirvió porque estábamos mal en las operaciones”.
S7: “Profe, lo bueno es el orden; el primer paso ayuda al segundo y así se resuelve rápido el problema”.
Subcategoría: Ejecutar el plan. En esta subcategoría se tuvo en cuenta, inicialmente, si los estudiantes cumplían con los planes diseñados para resolver los problemas, con el ánimo de identificar si estaban monitoreando y teniendo un control de sus procesos; por otra parte, se evaluó los procesos algorítmicos y cómo se sintieron o cómo actuaron en la ejecución de la subcategoría.
Con relación al cumplimiento de los planes diseñados, en su mayoría, los siguieron al pie de la letra y consideraron que seguir lo planeado era algo divertido. T3G6: “Los desarrollamos muy felices, con todo el amor y cariño; nos sentimos bien porque estábamos siguiendo lo que habíamos diseñado. Era muy divertido”.
Al ejecutar el tercer paso del método heurístico de George Pólya, los estudiantes en el taller de aplicación, a pesar de que el diseño de sus planes, en su mayoría, eran correctos, cometieron errores en los procesos aritméticos, fallaron al restar o dividir, presentando respuestas incorrectas a los problemas; por ejemplo, los integrantes de T2P1G1 diseñaron un plan adecuado para desarrollar el problema, pero en las operaciones que realizaron cometieron errores en una división y en una resta, procesos que dieron como consecuencia, respuestas incorrectas al problema.
Subcategoría: Mirar hacia atrás. Esta subcategoría pretendió generar en los estudiantes procesos de reflexión sobre lo llevado a cabo para encontrar la solución de los problemas. En el desarrollo que ellos le dieron a este cuarto paso del método heurístico de George Pólya, se evidenció que es la subcategoría a la que menos se habían dedicado; sin embargo, se debe considerar como un avance, el hecho de iniciar a revisar sus procesos, ya que es un aspecto que antes no lo hacían.
En la ejecución de los talleres de uso y aplicación del método heurístico de George Pólya se evidenció que, en el taller de aplicación, las respuestas que dieron los estudiantes carecían de revisión, aun cuando ellos consideraban que sí habían revisado el proceso, pues cometieron errores en multiplicaciones, restas y divisiones, errores que hubiera podido corregirse, si hubiesen realizado una buena revisión de sus procesos.
En la ejecución del taller de uso del método heurístico de George Pólya, se evidenció que la revisión se convirtió en un paso importante para los estudiantes, pues el desarrollo de sus procesos mejoró de una manera considerable, ya que presentaron operaciones, en su mayoría, correctas; además, plantearon problemas que cumplían con las condiciones establecidas, para lo cual se requería que ellos efectuasen unas revisiones acertadas para cumplir con las características solicitadas de los problemas.
Por otro lado, preguntarles si existía otro procedimiento más sencillo para desarrollar los problemas, los llevó a pensar en una solución alternativa, proceso que les permitió verificar lo que habían desarrollado, construir otro plan para ejecutar el problema y hacer uso de sus conocimientos previos.
El cumplimiento del objetivo específico dos se hizo a través de los talleres de uso y aplicación del método heurístico de George Pólya, lo cual llevó a la obtención de las categorías inductivas: Interpretación, Planteamiento y Revisión. En la taxonomía del objetivo específico 2 (ver Figura 3), se demuestra el avance que van adquiriendo los estudiantes gracias al uso del método heurístico de George Pólya, las clases lúdicas, el juego y la formación de grupos de forma estratégica.
De esta manera, el método heurístico de George Pólya se ha convertido en una ayuda para los estudiantes, al enfrentarse a problemas de operaciones combinadas, pues al presentarles los problemas, sabían lo que tenían que hacer; el orden de un método los guiaba para descubrir, en el problema, lo que debían buscar para solucionarlo y lo que tenían para desarrollarlo. Además, el método les ayudó a diseñar un plan, pero pensando en lo que necesitaban, como las operaciones y por donde debían iniciar. Cuando iniciaban, lo mentalizaban para no fallar, pues sus procedimientos requerían una revisión minuciosa.
El diseño de las clases en forma lúdica permitió que el método fuera aceptado, comprendido y memorizado más fácilmente por los estudiantes, pues a través de las clases donde el docente utilizó el papel de facilitador, ellos se empoderaron de su aprendizaje y fueron más independientes; se evidenció que empezaron a dejar la timidez y mejoraron su actitud, en comparación a la sesión 1.
En cuanto al juego, este aportó algo esencial a la investigación, pues hizo que los estudiantes comprendieran el objetivo de cada uno de los cuatro pasos del método, ya que sabían que se haría juegos para identificar el dominio del método que estaban adquiriendo; en esta fase, fue el grado de competitividad lo que los motivó a saber más del método.
Finalmente, la formación de grupos de estudiantes se realizó teniendo en cuenta su rendimiento académico; esto hizo que cada uno se sintiera útil, pues sus compañeros de grupo tenían competencias similares para la resolución de problemas. De igual manera, sabiendo que no existía en su grupo un compañero cuyas capacidades fueran potencialmente mayores a los suyas, los obligó a ubicarse en un mismo nivel de comprensión y a esforzarse cada vez más. Acorde con lo anterior, Marroquín (2015) considera que en el ‘aprendizaje cooperativo’, la organización grupal con un parámetro de igualdad presenta una alta valoración, pues incrementa las habilidades y competencias de sus miembros. A continuación, se presenta las categorías inductivas.
Categoría inductiva: Interpretación
En concordancia con Rosales y Salvo (2013), se considera a la interpretación como ese proceso de entender el enunciado del problema y, a la vez, ser capaz de crear información a partir del enunciado. Se infiere que los estudiantes, gracias a la aplicación y uso del método heurístico de George Pólya, cumplen con algunas etapas de las establecidas por estos autores, como la decodificación, el acceso al léxico, el análisis sintáctico, el análisis semántico, la interferencia y la producción de nuevos aprendizajes.
El cumplimiento de estas etapas, aunque no en profundidad, se convierte en un gran avance para los estudiantes, pues son procesos que en la prueba diagnóstica no realizaban. Lo desarrollado por ellos referente a esta categoría se agrupó en aspectos de asimilación y de actitud, como se describe a continuación:
Asimilación. La asimilación realizada por los estudiantes frente a los problemas planteados en los talleres de uso y aplicación de la estrategia, se evidenció cuando realizaron actividades como:
- Identificación de datos.
- Conocimiento del lenguaje natural (problemas del contexto de los estudiantes).
- Conocimiento del lenguaje matemático expresado en lenguaje natural.
- Utilización de los conocimientos previos.
a) Articulación de los conocimientos previos adquiridos en la resolución de problemas y los conocimientos nuevos que encontraron en la resolución de los problemas presentes en los talleres de uso y aplicación del método heurístico de George Pólya.
b) El llegar a la respuesta de la mayoría de los problemas.
Lo anterior evidencia la apropiación del método y el beneficio del mismo.
Actitud. La disposición de los estudiantes fue esencial para trabajar los problemas presentes en los talleres de uso y aplicación del método, pues esto permitió que empezaran a asumir la responsabilidad de su aprendizaje. Cabe aclarar que el docente es, en gran parte, el responsable de la actitud del estudiante al trabajar una temática, pues al presentar una clase lúdica, motiva al estudiante y le ayuda a comprender el método a través del juego y a confiar en sí mismo.
En resumen, la categoría inductiva Interpretación, muestra un avance significativo de los estudiantes en comparación con los resultados de la prueba diagnóstica. Se puede atribuir estos avances, en un primer momento, al uso y aplicación del método heurístico de George Pólya; posteriormente, se debe ser consciente de que las estrategias didácticas y lúdicas llevan a que el estudiante se motive por aprender y tenga una actitud positiva frente a la resolución de problemas con operaciones combinadas. Además, la evolución de los estudiantes fue un gran avance para llegar a la comprensión. Romero y Quintanilla (2019) expresan que la interpretación es un primer eslabón que debe realizar el estudiante para alcanzar la comprensión, esencial para solucionar cualquier tipo de problema.
Categoría inductiva: Planteamiento
En esta categoría se abarcó lo que se evidenció en los procesos realizados por los estudiantes con relación al planteamiento de problemas. Inicialmente, es necesario considerar como aspecto fundamental, el contexto al momento de plantear y solucionar problemas. Los resultados de la investigación evidencian que es mucho más sencillo para los estudiantes plantear problemas del contexto o de temas que les agraden. Con base en esto, Rosales y Salvo (2013) afirman que los enunciados de los problemas deben aludir a experiencias o contextos familiares para ellos; en caso contrario, pueden llegar a presentar planteamientos inadecuados o planteamientos en donde se deje de lado algunos aspectos que se debe considerar en los problemas. Lo dicho afecta, ya sea positiva o negativamente, su actitud. Esto se presenta porque al conocer el contexto del problema, la actitud por parte de ellos será positiva; asimismo, se evidencia afectividad e interés por plantear este tipo de problemas; caso contrario ocurre cuando el contexto es poco o nada conocido, pues se evidencia preocupación, poca coherencia del problema y desmotivación, llevando a que se sientan incapaces de plantear el problema y que cumplan con las características solicitadas.
Se evidenció que la mayoría de los estudiantes realizaron una interpretación adecuada, inicialmente de lo que pedía cada problema para desarrollarlo; posteriormente, se observó que llegaban a cumplir con las solicitudes de la mayoría de los problemas. Esto daba fe de que se estaban encaminando hacia lo requerido por el MEN (2006). Por lo tanto, se nota que, al trabajar la resolución de problemas en grado sexto, se está aportando y trabajando con lo establecido en supervisiones institucionales. De igual manera, el planteamiento de problemas demostró a los estudiantes la importancia de la generación de ideas y de su contexto.
Generación de ideas. Con base en lo analizado en el desarrollo de las sesiones 2, 3 y 4, se observa que, para el planteamiento de un problema, la generación de ideas es fundamental, por cuanto permiten crear una situación coherente y llamativa para el estudiante. La generación de ideas despierta, por una parte, su creatividad, pues lo lleva a crear situaciones problémicas nuevas y, por otra, genera pertinencia.
Contexto. En los estudiantes, el plantear problemas donde se les daba la libertad de elegir el contexto de los mismos, generó el gusto por los problemas y por el método. En consonancia, Rosales y Salvo (2013) sostienen que los enunciados de los problemas deben aludir a experiencias o contextos familiares para el estudiante, ya que esto permitirá construir un problema de temas que conocen y que les gusten. Asimismo, al plantear problemas, se está cumpliendo condiciones matemáticas que les lleva a que trabajen y adquieran dominio en los conceptos matemáticos y el método heurístico de George Pólya.
Categoría inductiva: Revisión
La revisión de los procesos desarrollados por los estudiantes los ha llevado a realizar correcciones en cuanto al desarrollo de procesos aritméticos, a cambiar de plan en caso de ser necesario y han llegado a sentir éxito por haber diseñado y realizado bien sus procesos.
El buscar plantear otro plan para desarrollar el problema y no llegar a la misma solución permite ver dónde está el error y en cuál procedimiento, pues dicho error puede estar en cualquiera de los tres pasos que desarrollaron para llegar a la solución del problema.
Si bien es cierto que aún falta mucho para que los estudiantes encuentren dos o más métodos para desarrollar un problema, esta revisión, como la considera Pólya (citado por Aguilar, 2014), es más que necesaria para que identifiquen si han llegado o no a la meta y, además, evalúen sus procesos, con el fin de analizar si el uso que están dando a sus conocimientos previos es el adecuado. Cabe mencionar que esta categoría inductiva se vio beneficiada, gracias al trabajo en equipo.
Trabajo en equipo. La revisión es una parte esencial que el estudiante debe realizar al momento de desarrollar un problema; revisión que, en el desarrollo de la investigación, se fortificó gracias al trabajo colaborativo, pues éste permitió:
- Crear mejores relaciones entre los estudiantes.
- Valorar las habilidades de sus compañeros y las suyas.
- Expresar ideas claramente.
- Despertar el interés de aprender.
- Generar empoderamiento.
Aldana (2012) manifiesta que se debe ser consiente que, a medida que tanto docentes como estudiantes intercambien experiencias con los demás, el aprendizaje será significativo; de lo contrario el estudiante no aprenderá mucho, si solo está sentado en clases escuchando a sus profesores, memorizando los conocimientos impartidos, realizando preguntas y emitiendo respuestas. Este autor afirma que es fundamental que los estudiantes hablen de lo que están aprendiendo, lo relacionen con su entorno y lo apliquen a su vida diaria.
Autores como Paul Roeders y Henry Ford (citados por Aldana, 2012) consideran que los niveles de procesamiento de la información en el ser humano son desarrollados, principalmente, en el ‘haciendo y exponiendo’, considerando el trabajar juntos como un éxito, obteniendo así el aprendizaje cooperativo con el que se logra manejar la información, reflexionar sobre ella y desarrollar en los estudiantes habilidades relacionadas con el liderazgo y el trabajo en equipo.
En el desarrollo de esta investigación se formó grupos teniendo en cuenta el rendimiento académico de los estudiantes, lo cual demostró que sus habilidades pudieran ser potencializadas, tal como se evidencia en los resultados del taller evaluativo, donde estos trabajaron de manera organizada, teniendo control de sus procesos y mostrando dominio del método y comprensión de los problemas. Marroquín (2015) valida esta forma de organización grupal.
Lo elaborado en el cumplimiento del segundo objetivo específico es una muestra del avance que ha generado en los estudiantes el método heurístico de George Pólya, avance que fue fortificado con el trabajo en grupo, pues la formación de grupos de estudiantes llevó a que cada uno se sintiera útil.
Objetivo específico 3. Evaluación alternativa en la resolución de problemas con operaciones combinadas.
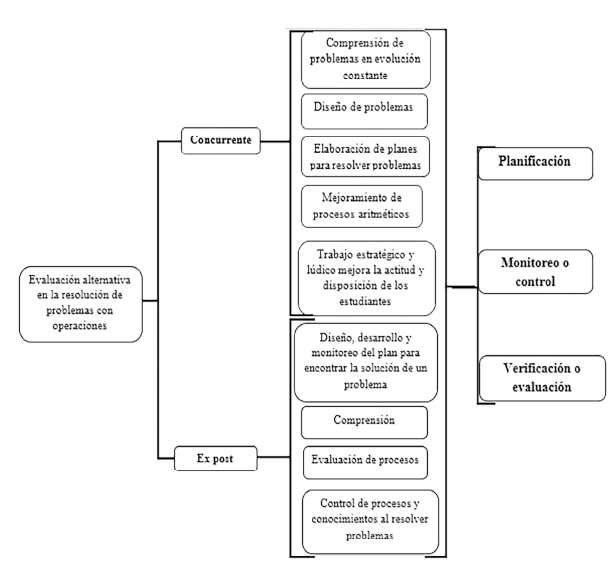
Códigos taxonomía 3:
Categoría deductiva: Evaluación alternativa en la resolución de problemas con operaciones.
Subcategorías: Concurrente, Ex post.
Categorías inductivas: Planificación, Monitoreo o control, Verificación o Evaluación.
El análisis e interpretación de los resultados obtenidos en la ejecución del objetivo específico 3 busca evaluar los desempeños de los estudiantes en la resolución de problemas matemáticos con operaciones combinadas a través del método heurístico de George Pólya; esto se realizó mediante la categoría deductiva Evaluación alternativa en la resolución de problemas con operaciones combinadas, conformada por las subcategorías Concurrente y Expost, donde su análisis permitió extraer las categorías inductivas Planificación, Monitoreo o control y Verificación o evaluación.
La Figura 3 contempla las características que surgieron en la ejecución del tercer objetivo específico y en los resultados de los objetivos específicos uno y dos. Se considera el proceso completo de la investigación, ya que la evaluación alternativa es procesual y busca evidenciar las mejoras que adquieren los estudiantes a través del tiempo mediante el uso de estrategias (Valverde y Valverde, 2017). Hecha esta salvedad, en la Figura 3 se muestra que los estudiantes adquirieron la habilidad de comprender los problemas, diseñaron planes adecuados para resolverlos y, al ejecutarlos, fueron mucho más cautelosos que en el desarrollo de la prueba diagnóstica.
En consonancia, Boscán y Klever (2012) afirman que, al presentar el método heurístico de George Pólya a los estudiantes al momento de resolver problemas matemáticos, estos tienen un aumento significativo en la comprensión y resolución del problema. No obstante, también es necesario mencionar que en la presente investigación se hizo uso de la lúdica y el juego, como herramientas potenciales para generar un cambio de actitud en los estudiantes, lo cual permitió la aceptación tanto del método heurístico como la resolución de problemas.
En la aplicación del taller evaluativo, los estudiantes evidenciaron un interés hacia la resolución de problemas y al método heurístico de George Pólya, sin desaprovechar el tiempo. Conviene subrayar que se realizó una evaluación formal, tal como se desarrolló la prueba diagnóstica, con la diferencia de que ellos ya conocían el método heurístico de George Pólya, herramienta indispensable para desarrollar un problema matemático.
La categoría Evaluación alternativa en la resolución de problemas matemáticos con operaciones combinadas analizó si los estudiantes le daban un uso adecuado al método heurístico de George Pólya al momento de desarrollar problemas de operaciones combinadas, así como el desarrollo que les daban a los mismos; su fin era identificar las mejoras que los estudiantes habían tenido en cuanto a estos aspectos (Valverde y Valverde, 2017).
Para el desarrollo de la evaluación alternativa, es necesario mencionar que se hizo uso de una rúbrica, diseñada con base en el método heurístico de George Pólya, cuyo soporte de evaluación fue el plan de área de la institución, el cual contempla tanto el sistema de calificación utilizado en la rúbrica, como el método en mención. A causa de esto, se obtuvo la calificación numérica del taller evaluativo. La categoría consta de dos subcategorías: Concurrente y Ex post.
Subcategoría: Concurrente. Esta subcategoría evalúa el momento procesual del estudiante, para lo cual se debe considerar el avance que ha tenido en el desarrollo de la investigación. Hace referencia a una función evaluadora permanente y durante el proceso (Valverde y Valverde, 2017).
En el transcurso de la investigación, fue clara la mejoría de los estudiantes, pues la comprensión de problemas, a medida que fueron adquiriendo dominio del método heurístico de George Pólya, evolucionó en forma considerable; de esta forma, en la ejecución del segundo objetivo específico, estos empezaron a asimilar e interpretar el método y los problemas; y, en el desarrollo del taller evaluativo, extrajeron datos de un problema, comprendieron lo que debían buscar para solucionarlos, diseñaron planes adecuados para resolverlos, eligieron operaciones correctas y razonaron sobre sus propios procedimientos, aspectos que en la prueba de conocimiento de problemas con operaciones combinadas no hacían.
Además, memorizaron el método y comprendieron cuál era la función de cada uno de los pasos que éste contiene, aspecto favorable para la investigación, pues permitió que tuvieran dominio del método y empezaran a razonar más sobre los aspectos relevantes del problema; esto, a la vez, les permitió comprender más, tanto los problemas como sus formas de razonar y actuar ante los mismos. Por ejemplo, el S4, en el taller evaluativo, sin ayuda del docente, describió y usó los cuatro pasos del método heurístico de George Pólya, trabajándolo con claridad y conservando su orden.
Asimismo, los estudiantes adquirieron una excelente habilidad para diseñar problemas, especialmente aquellos donde se les dio la libertad de asignar el contexto que ellos desearan, pero cumpliendo condiciones matemáticas. Lo anterior les llevó a que, además de diseñar los problemas, construyeran planes para desarrollarlos, monitoreando el desarrollo que iban dando y el cumplimiento de condiciones. Asimismo, la revisión que realizaban, se evidenció en el mejoramiento de procesos aritméticos, pues de 60 procedimientos realizados, solamente cuatro fueron incorrectos.
En este punto es necesario resaltar el trabajo en grupo, el cual, si es organizado de manera estratégica, brinda ayudas a los estudiantes, pues les permite desarrollarse en sociedad y comprender la forma de razonar de otras personas, corroborando sus conocimientos y aceptando sus errores con argumentaciones.
Con relación al desarrollo de los estados emocionales de los estudiantes, estos también tuvieron un gran avance, pues de un estado de estrés, tristeza, preocupación, angustia y enojo, pasaron a sentir emociones de alegría, empezaron a creer que eran capaces de desarrollar problemas y, eso es muy gratificante. Por ejemplo, al responder el cuestionario del taller evaluativo, donde se les preguntó si creían que el método heurístico les aportaría para responder el taller evaluativo, algunas respuestas fueron: S11: “Sí, me ha servido y mucho, porque con este método he desarrollado más mi mente e imaginación y se me ha hecho más fácil responder los problemas”. S8: “Pues sí, porque así he resuelto los problemas mucho más rápido y con más facilidad. Y no es difícil resolver todos los problemas con el método heurístico de George Pólya”.
Subcategoría Ex post. Teniendo en cuenta los procesos desarrollados por los estudiantes, evaluados con base en la rúbrica y al proceso desarrollado antes, durante y después del uso del método heurístico de George Pólya, se evidenció que tuvieron un avance significativo respecto a los resultados de la prueba diagnóstica.
Entre los avances encontrados, se logró identificar que la mayoría de los estudiantes adquirieron la capacidad de extraer datos de un problema, diseñar un plan, realizar operaciones y revisar si sus procesos eran correctos. Esto les permitió mejorar sus procesos metacognitivos ya que, inicialmente, extraían e identificaban lo que debían buscar para solucionar un problema y diseñaban un plan para resolverlo. Posteriormente, comenzaron a tener un control de su plan o monitorear los procesos que iban desarrollando y, finalmente, comprendían la importancia de evaluar los procesos que habían realizado.
En lo referente a la calificación que se daba a los estudiantes con base en la rúbrica, estos fueron débiles en evaluarse a sí mismos, pues solo consideraban que la evaluación se centraba en revisar los procesos matemáticos y no en la escritura o diseño del plan, que son parte fundamental del proceso del desarrollo.
Los resultados numéricos son favorables, pues solo uno de doce estudiantes obtuvo resultados inferiores a 3. Cuatro estudiantes obtuvieron calificaciones entre 3.0 y 4.0; finalmente, siete estudiantes obtuvieron calificaciones superiores a 4.
Lo anterior evidencia el uso adecuado que los estudiantes le dieron al método heurístico de George Pólya, así como la capacidad que adquirieron al resolver problemas con operaciones combinadas con el uso de dicho método.
Los resultados de la investigación, con relación al tercer objetivo específico, permitieron identificar las categorías inductivas: Planificación, Monitoreo o control y Verificación o evaluación, descritas a continuación:
Categoría inductiva: Planificación
El aporte que realiza el método heurístico de George Pólya se identifica en el avance de los estudiantes, tanto al comprender los problemas como al diseñar un plan para desarrollarlos. Ese ‘diseñar un plan’, según Díaz et al. (citados por Arroyo, Korzeniowski y Espósito, 2014), es considerado como la planificación que implica “anticipar consecuencias, generar y seleccionar alternativas que permitan evocar un mapa mental que sirva para dirigir la acción al logrado de un objetivo” (p. 55); esto convierte a la acción de planeación, en una acción compleja que requiere o pone en juego diversas funciones al momento de resolver un problema, por lo cual, cuando un estudiante se enfrenta a un problema, es capaz de diseñar un plan para resolverlo, desencadenando que su desarrollo cognitivo progrese considerablemente.
Esta categoría potencializa en el estudiante la planeación y organización mental, con base en los resultados obtenidos en la investigación, referentes a los aspectos conceptuales, procedimentales y actitudinales que presentaron los estudiantes durante la aplicación de los instrumentos.
Planeación. Alude al dominio de los conocimientos que los estudiantes han adquirido en el desarrollo de la investigación; es ese ‘pensar antes de actuar’, buscando formas, caminos y procesos que ayuden a llegar a la meta deseada. Los estudiantes, antes del método, no realizaban procesos de planeación; en el taller evaluativo, la planeación pasó a ser un lugar central en sus desarrollos.
Organización mental. Con lo desarrollado, se evidenció que los estudiantes empezaron a realizar esquemas mentales al momento de diseñar planes para resolver problemas, ya que, inicialmente, al diseñar un plan, identificaban la meta a la que debían llegar y con lo que contaban para llegar a ella; posteriormente, integraron a esas ideas, operaciones que relacionaban los datos identificados y que les permitían obtener resultados que los acercaran a su meta.
Categoría inductiva: Monitoreo o control
Al desarrollar problemas con operaciones combinadas haciendo uso del método heurístico de George Pólya, se evidenció que los estudiantes adquirieron la habilidad de tener un control sobre sus procesos al momento de resolver los problemas. Esto les permitió controlar su trabajo, identificando si era correcto el plan diseñado o si debían abandonarlo para iniciar uno nuevo.
Lo anterior es fundamental para ellos al momento de enfrentarse a un problema, pues les permite, según Schoenfeld (citado por Barrantes, 2006), tener conocimiento de sí mismos, adquiriendo la habilidad de identificar tanto los conocimientos que poseen, como su forma de actuar ante diversos procesos o situaciones. Además, al tener dominio de los procesos que desarrollan, son autónomos en el proceso de enseñanza-aprendizaje, pues son ellos quienes regulan sus conocimientos y procedimientos, llevándolos a sentir un grado de satisfacción, motivación y alegría ante la resolución de problemas. Por lo tanto, los estudiantes de grado sexto hicieron un aprendizaje efectivo y autorregulador a través del método heurístico de George Pólya.
Aprendiz efectivo. Los estudiantes de grado sexto, en el proceso de desarrollo de la investigación, demostraron cumplir con las características de un aprendiz efectivo, pues adquirieron la habilidad de comprender el método heurístico de George Pólya, utilizarlo adecuadamente, y cuando lo hacían, ponían en juego los conocimientos, ideas y creencias que habían adquirido. Es efectivo, ya que “se siente agente de su comportamiento estando automotivado, usando estrategias de aprendizaje para lograr resultados académicos deseados, autodirigiendo la efectividad de su aprendizaje, evaluándolo y retroalimentándolo” (Marroquín, 2015, p. 111).
Autorregulador. Los estudiantes, gracias al aprendizaje del método heurístico de George Pólya, empezaron a generar revisión constante de sus procesos; por ejemplo, cuando regulaban la selección y uso de sus conocimientos, ideas y creencias, cuando construían, planificaban, controlaban y evaluaban procesos necesarios para resolver problemas. Marroquín (2015) considera que los estudiantes son reguladores cuando son cognitiva, motivacional y conductualmente los que dirigen, asumen y verifican sus procesos de aprendizaje, pues toman decisiones acertadas y regulan el uso de sus conocimientos, diseñan planes que los ayudan para llegar a la meta y son persistentes en hacerlo.
Lo evidenciado en el desarrollo del objetivo específico 3, el cual abarca el proceso de los estudiantes antes, durante y después de conocer y usar el método heurístico de George Pólya, da una luz de los aportes del método, no solo en la resolución de problemas, sino también en lo actitudinal y lo conceptual del estudiante.
Categoría inductiva: Verificación o evaluación
La verificación o evaluación de los procesos que realizan los estudiantes es débil, en comparación con los procesos de comprensión y desarrollo de los problemas; esto se debe a que anteriormente no tenían la costumbre de hacer una revisión de sus procesos o, simplemente, consideraban que eran los adecuados.
Sin embargo, el hacer uso del método heurístico de George Pólya en la resolución de problemas matemáticos, les ha llevado a comprender la importancia de la verificación, por cuanto empezaron a monitorear sus procesos y, con ello, a evaluarlos. No obstante, dicha evaluación debe consistir en evaluar tanto los procedimientos aritméticos como el uso adecuado de métodos o estrategias utilizados para la resolución de un problema (MEN, 1998).
Con base en la postura del estudiante sobre sus procedimientos, surgen como características de esta categoría inductiva, la autoevaluación y la valoración, descritas a continuación:
Autoevaluación. Esta característica se da por el procedimiento de evaluación que realizaron los estudiantes a sus propios procedimientos. En consonancia con Marroquín (2015), les ayuda a incrementar la autoconciencia de su propio aprendizaje, permitiéndoles despertar su rol crítico y curioso, ya que deben analizar sus procesos y buscar otras formas de llegar a la solución de un problema, con el fin de presentar un proceso más sofisticado, identificar falencias de sus procesos iniciales o ratificar la exactitud de ellos.
Valoración. El hecho de que los estudiantes revisen y evalúen lo que han realizado, ha llevado a que generen una valoración tanto a sus propios procesos como a sus capacidades y aptitudes. Marroquín (2015) considera que el intentar explicar y evaluar sus procedimientos, demuestra las motivaciones y creencias personales que disponen para realizar y evaluar sus tareas.
4. Conclusiones
Los estudiantes de grado sexto se enfrentan a dar solución a problemas con operaciones combinadas de manera tradicional, lo que permite dar cuenta de algunos aspectos; entre estos se menciona que carecen de los conocimientos previos al momento de comprender el problema, mostrando su grado de abstracción con el mismo, o al momento de desarrollar procedimientos, dado que se evidencia fallas en el desarrollo de las diversas operaciones. Con relación a ello, Parodi (citado por Rosales y Salvo, 2013) considera que la comprensión es el proceso que permite elaborar el significado de un texto con las ideas que ya se tiene. Así, con base en que la comprensión de los estudiantes es débil, pues no comprenden lo que leen ni tienen las herramientas disciplinares para resolver los problemas matemáticos, necesitan mejorar el proceso de comprensión. Fundamentado en los DBA, es más que necesario que sean capaces de comprender e interpretar contenidos matemáticos en diversos contextos al resolver problemas.
El uso y aplicación del método heurístico de George Pólya cumple con algunas etapas de las establecidas por Rosales y Salvo (2013), aspectos que en la prueba diagnóstica no los cumplían. Estos avances pueden ser atribuidos, en un primer momento, al uso y la aplicación del método heurístico de George Pólya; posteriormente, se requiere ser consciente que las estrategias didácticas y lúdicas conducen al estudiante a motivarse por aprender y tener una actitud positiva frente a la resolución de problemas con operaciones combinadas. De ahí que, la evolución que han tenido los estudiantes es un gran avance para llegar a la comprensión, pues, de acuerdo con Romero y Quintanilla (2019), la interpretación es un primer eslabón que debe realizar el estudiante para alcanzar la comprensión, esencial para solucionar cualquier tipo de problema y, por ende, generar la autonomía y regulación de los procesos de enseñanza y aprendizaje.
La verificación o evaluación de los procesos que realizaban los estudiantes de grado sexto se presentó débil, en comparación con los procesos de comprensión y desarrollo de los problemas; esto fue un indicador de la carencia del hábito de realizar una revisión de los procesos aritméticos. Sin embargo, al hacer uso del método heurístico de George Pólya en la resolución de problemas matemáticos, les ha generado, como prioridad, comprender la importancia de la verificación, pues da inicio a monitorear los procesos aritméticos con el fin de evaluarlos. Dicha evaluación consiste en evaluar tanto los procedimientos aritméticos como el uso adecuado de métodos o estrategias utilizados para la resolución de un problema.
5. Conflicto de intereses
Las autoras de este artículo declaran no tener ningún tipo de conflicto de intereses del trabajo presentado.
Referencias
Aguilar, B. (2014). Resolución de problemas matemáticos con el Método de Pólya mediante el uso de Geógebra en primer grado de secundaria (Tesis de Maestría). Tecnológico Monterrey, Tolima, Colombia. Recuperado de https://repositorio.tec.mx/handle/11285/626537
Aldana, C. (2012). Trabajo colaborativo en el área de matemáticas. Blanco y Negro, 3(1), 26-35.
Arroyo, M., Korzeniowski, C. y Espósito, A. (2014). Habilidades de planificación y organización, relación con la resolución de problemas matemáticos en escolares argentinos. Centro de documentación, Investigación y Difusión de Psicología científica, Eureka, 11(1), 55-64.
Boscán, M.M. y Klever, K.L. (2012). Metodología basada en el método heurístico de Pólya para el aprendizaje de la resolución de problemas matemáticos. Escenarios, 10(2), 7-19.
Barrantes, H. (2006). Resolución de problemas. El trabajo de Allan Schoenfeld. Cuadernos de investigación y formación en educación matemática, 1(1), 1-9.
Barrera-Mora, F. y Reyes-Rodríguez, A. (2017). Tareas con diversas soluciones: estructuras conceptuales en profesores de matemáticas. Revista Electrónica de Investigación Educativa, 19(1), 110-122. DOI: https://doi.org/10.24320/redie.2017.19.1.971
Calvo, M. (2008). Enseñanza eficaz de la resolución de problemas matemáticos. Educación Matemática 32(1), 123-138.
Derazo, D. y Riascos, J. (2018). Errores en el aprendizaje de la adición y sustracción de números racionales positivos en notación fraccionaria (Tesis de Maestría). Universidad Mariana, Nariño, Colombia.
Díaz, V., Belmar, H. y Poblete, A. (2018). Manifestación emocional y modelación de una función matemática. Bolema, Río Claro, 32(62), 1198-1218. DOI: http://dx.doi.org/10.1590/1980-4415v32n62a22
Echenique, I. (2006). Matemáticas, resolución de problemas. Navarra, España: Gobierno de Navarra.
Gómez, A. (2010). El proceso de enseñanza-aprendizaje de los conceptos de ordenación y combinación con estudiantes de educación superior: Un enfoque basado en la resolución de problemas (Tesis doctoral). Universidad Autónoma de Barcelona. Recuperado de https://www.educacion.gob.es/teseo/imprimirFicheroTesis.do?idFichero=LYcyteLZX58%3D
Guerrero, E. y Blanco, L. (2004). Diseño de un programa psicopedagógico para intervención en los transtornos emocionales en la enseñanza y aprendizaje de las matemáticas. Revista Iberoamericana de Educación, 34(2), 1-14. DOI: https://doi.org/10.35362/rie3422990
Hernández, R., Fernández, C. y Baptista, M. (2014). Metodología de la investigación (6.a ed.). Santa Fe, México: McGraw-Hill / Interamericana Editores, S.A. de C.V.
Latorre, A., Rincón, D. y Arnal, J. (2003). Bases metodológicas de la investigación educativa. Barcelona, España: Ediciones Experiencia.
Mamani, F. y Villalta, B. (2017). Aplicación del método heurístico de Pólya en la resolución de problemas con las cuatro operaciones básicas en los estudiantes de sexto grado de primaria de la Institución Educativa Particular Latinoamericano del Distrito de Paucarpata – Arequipa, 2016 (Trabajo de Grado). Universidad Nacional de San Agustín de Arequipa, Perú. Recuperado de http://repositorio.unsa.edu.pe/handle/UNSA/4269.
Marroquín, M. (2015). Docentes estratégicos forman estudiantes estratégicos. Una propuesta para el trabajo de aula. San Juan de Pasto, Colombia: Editorial Unimar.
Ministerio de Educación Nacional (MEN). (1998). Serie Lineamientos Curriculares – matemáticas. Recuperado de https://www.mineducacion.gov.co/1621/articles-89869_archivo_pdf9.pdf
Ministerio de Educación Nacional (MEN). (s.f.). Derechos Básicos de Aprendizaje (DBA). Matemáticas 6. Recuperado de http://aprende.colombiaaprende.edu.co/sites/default/ files/naspublic/DBA_Matem%C3%A1ticas.pdf.
Ministerio de Educación Nacional (MEN). (2006). Estándares básicos de competencias en matemáticas. Recuperado de https://www.mineducacion.gov.co/1621/articles-340021_recurso_1.pdf
Monereo, C., Castelló, M., Clariana, M., Palma, M. y Pérez, M. (1999). Estrategias de enseñanza y aprendizaje. Formación del profesorado y aplicación en la escuela (6.ª ed.). Barcelona, España: Editorial Graó.
Romero, G. y Quintanilla, V. (2019). El círculo hermenéutico de la comprensión en matemáticas: una propuesta integradora para la evaluación en el aula. Revista Latinoamericana de Investigación en Matemática Educativa, 22(1), 97-122.
Rosales, M. y Salvo, E. (2013). Influencia de la Comprensión Lectora en la Resolución de Problemas Matemáticos de Contexto en estudiantes de quinto y sexto año básico de dos establecimientos municipales de la comuna de Chillán (Trabajo de Grado). Universidad Bío-Bío, Chillán. Recuperado de http://repobib.ubiobio.cl/jspui/bitstream/123456789/1868/1/Rosales_Molina_Maria.pdf
Ruiz, F. (2017). Las estrategias heurísticas y la resolución de problemas de los estudiantes del tercer año de secundaria de la I.E. N°_ 6094 “Santa Rosa”, Chorrillos; Lima, 2016 (Tesis de Maestría). Universidad César Vallejo, Perú. Recuperado de http://repositorio.ucv.edu.pe/handle/20.500.12692/5622?locale-attribute=en
Silva, M., Rodríguez, A. y Santillán, O. (s.f.). Estrategias de resolución de problemas matemáticos empleadas por alumnos de sexto de primaria. X Congreso Nacional de Investigación Educativa. Veracruz, México. Recuperado de http://webcache.googleusercontent.com/search?q=cache:Obs5awDnWAgJ:www.comie.org.mx/congreso/memoriaelectronica/v10/pdf/area_tematica_05/ponencias/1729-F.pdf+&cd=1&hl=es&ct=clnk&gl=co&client=firefox-b-d
Universidad Mariana. (s.f.). Facultad de Posgrados y Relaciones Internacionales, Maestría en Pedagogía. Formación y Práctica Pedagógica. Recuperado de http://www.umariana.edu.co/pedagogia/5-INVESTIGACION/ANEXO%2025.%20Documento%20Linea%20investigaci%C3%B3n%20Grupo%20INDAGAR.pdf
Valverde, Y. y Valverde, O. (2017). Conocimiento práctico de la evaluación, Sentido del Profesorado y Evaluación para el aprendizaje y el Desarrollo de las Competencias. San Juan de Pasto, Colombia: Editorial UNIMAR.

