Resumo: Aborda-se, neste artigo, a metodologia da Resolução de Problemas, desenvolvida na prática educativa da matemática como metodologia de ensino de Matemática que propicia aos estudantes caminho para que se tornem cidadãos capazes de intervir de maneira crítica e criativa em várias situações dentro de diferentes contextos. Para a presente elaboração, foi necessária uma construção teórica amparada nas produções sobre a metodologia de Resolução de Problemas, de Dante (2003), Onuchic (2013), Onuchic e Alevatto (2004), Polya (1995), Pozo e Echeverría (1998) e as tecnologias, de Borba e Penteado (2003). Essa revisão seguiu uma abordagem amparada por eixos categorizados sobre a metodologia Resolução de Problemas, para interpretar as informações dos autores que dialogam sobre a temática, com o objetivo de construir uma proposta de atividade para ensino de congruência de triângulos (unidade temática Geometria), utilizando ferramentas tecnológicas (software GeoGebra). Assim, buscaremos respostas sobre como construir uma proposta de atividade que engloba esse contexto. As leituras realizadas nos mostraram que não se pode mecanizar o ensino da metodologia Resolução de Problemas e que a condução dos estudantes, por intermédio de perguntas, pode torná-los independentes para a resolução de problemas.
Palavras-chave: Resolução de Problemas, GeoGebra, Ensino, Conceitos Geométricos.
Abstract: This article discusses the Problem Solving methodology, developed in the educational practice of mathematics as a teaching methodology in Mathematics that provides the student with the path to become citizens capable of intervening in a critical and creative way in various situations within different contexts. For this elaboration, it was necessary a theoretical construction supported by the productions on the Problem Solving methodology, by Dante (2003), Onuchic (2013), Onuchic and Alevatto (2004), Polya (1995), Pozo and Echeverría (1998) and technologies, by Borba and Penteado (2003). This review followed an approach supported by categorized axes on the Problem Resolution methodology, to interpret the information of the authors who dialogue on the theme, with the objective of building an activity proposal for teaching congruence of triangles (thematic unit Geometry), using technological tools (GeoGebra software). Thus, we will seek answers on how to build an activity proposal that encompasses this context. The readings carried out showed us that it is not possible to mechanize the teaching of the Problem Solving methodology and that the conduct of students, through questions, can make them independent for solving problems.
Keywords: Problem Solving, GeoGebra, Teaching, Geometric Concepts.
Resumen: En este artículo se analiza la metodología de Resolución de Problemas, desarrollada en la práctica educativa de la matemática como una metodología de enseñanza en Matemática que brinda al estudiante el camino para convertirse en ciudadano capaz de intervenir de manera crítica y creativa en diversas situaciones dentro de diferentes contextos. Para esta elaboración fue necesaria una construcción teórica sustentada en las producciones sobre la metodología de Resolución de Problemas, de Dante (2003), Onuchic (2013), Onuchic y Alevatto (2004), Polya (1995), Pozo y Echeverría (1998) y tecnologías, por Borba y Penteado (2003). Esta revisión siguió un enfoque apoyado en ejes categorizados sobre la metodología de Resolución de Problemas, para interpretar la información de los autores que dialogan sobre el tema, con el objetivo de construir una propuesta de actividad para la enseñanza de la congruencia de triángulos (unidad temática Geometría), utilizando herramientas tecnológicas. (Software GeoGebra). Así, buscaremos respuestas sobre cómo construir una propuesta de actividad que englobe este contexto. Las lecturas realizadas nos mostraron que no es posible mecanizar la enseñanza de la metodología de Resolución de Problemas y que la conducta de los estudiantes, a través de preguntas, puede hacerlos independientes para la resolución de problemas.
Palabras clave: Solución de problemas, GeoGebra, Enseñando, Conceptos Geométricos.
Educação Matemática
ENSINO DE CONGRUÊNCIA DE TRIÂNGULOS: RESOLUÇÃO DE PROBLEMAS MEDIADA PELO SOFTWARE GEOGEBRA
TRIANGLE CONGRUENCE TEACHING: PROBLEM SOLVING MEDIATED BY THE GEOGEBRA SOFTWARE
ENSEÑANZA DE LA CONGRUENCIA DEL TRIÁNGULO: RESOLUCIÓN DE PROBLEMAS MEDIADA POR EL SOFTWARE GEOGEBRA
Recepção: 09 Abril 2021
Aprovação: 12 Maio 2021
Publicado: 02 Junho 2021

Um dos movimentos fundamentais que rege as mudanças e está registrado nas diferentes pesquisas educacionais é o de orientar os estudantes a compreenderem a necessidade de aprender a aprender, essa capacidade proporcionará o desenvolvimento das competências[1] e das habilidades que são úteis para a construção do conhecimento sobre a cultura, a ciência, a tecnologia, a sociedade e o ambiente. O estudante que aprende a aprender na perspectiva freiriana tornar-se-á um cidadão capaz de intervir de maneira crítica e criativa em várias situações, dentro de diferentes contextos, construindo conhecimentos a partir daqueles que já possui, almejando uma melhor qualidade de vida.
De posse dessa ideia citada no parágrafo anterior, o caminho para o desenvolvimento desta pesquisa será bibliográfico, que, conforme Gil (2002), é o tipo de pesquisa desenvolvida tendo como base materiais já elaborados, possuindo como principais fontes de consulta livros e artigos científicos. Além disso, a pesquisa aqui proposta possui uma abordagem qualitativa, pois procuramos destacar o processo de resolução da situação e não somente o resultado final, estivemos amparados por eixos categorizados sobre a metodologia Resolução de Problemas, para, assim, conceber uma análise da proposta da atividade.
Por intermédio dos tratados de Onuchic e Allevato (2004) e de Onuchic (2013), podemos verificar que ensinar matemática por meio da Resolução de Problemas é uma alternativa de ensino que ainda enfrenta dificuldades que precisam ser superadas. Essa superação pode ocorrer por meio da construção de alternativas que fazem o uso da metodologia Resolução de Problemas para o ensino da Matemática desde os anos iniciais da educação básica, pois, desse modo, é possibilitado aos estudantes momentos que exigem grande esforço e dedicação para entender, pensar, resolver, lidar, explicar e elaborar problemas advindos de situações do cotidiano e, consequentemente, construir competência para:
Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções (BRASIL, 2018, p. 267).
Temos, neste estudo, o objetivo de construir e de apresentar aos professores uma alternativa de ensino para a unidade temática Geometria, utilizando a Resolução de Problemas de Polya (1995) como metodologia de ensino mediada pelo software GeoGebra. Compreende-se que, para trabalhar com essa metodologia, é necessário seguir quatro etapas: 1ª etapa – Compreensão do problema, 2ª etapa – Construção de uma resolução, 3ª etapa – Execução escolhida e 4ª etapa – Revisão da solução. Desta maneira, buscaremos respostas referentes a como construir uma proposta de atividade que englobe o contexto relatado.
A Resolução de Problemas surge como alternativa para o ensino nos Estados Unidos, na década de 1960, sob a influência de George Polya (1887-1985). Conforme estudos realizados por Fiorentini (1994), entre 1896 e 1904, havia experiências e estudos similares desenvolvidos por John Dewey (1859-1952). Nessas experiências, as crianças estudavam por meio de projetos que reproduziam as situações socioeconômicas (estudo/Resolução de Problemas de interesse da comunidade) e que sugeriam que essa orientação pedagógica pudesse contribuir para o desenvolvimento do espírito crítico das crianças, capacitando-as para que contribuíssem para o desenvolvimento de uma sociedade democrática.
Sobre essa situação, Onuchic (2013, p. 04) enfatiza que:
[...] ensinar Resolução de Problemas significava apresentar problemas e, talvez, incluir uma técnica de resolução específica [...] chamando a atenção para fatos da vida real, mas sempre com alguém resolvendo o problema e deixando-se uma lista com problemas semelhantes para serem resolvidos.
Com o avanço dos estudos sobre a Metodologia da Resolução de Problemas, Onuchic (2013) e Polya (1995) corroboram com a ideia de que a Resolução de Problemas consiste em proporcionar que os educandos utilizem seus conhecimentos e desenvolvam a capacidade de administrar as informações ao seu redor.
Desse modo, essa metodologia para ensinar a Matemática aos estudantes auxilia no enfrentamento de novas situações e no desenvolvimento do raciocínio matemático, uma vez que ensinar a Matemática, de acordo com Pozo e Echeverría (1988), por intermédio da utilização da Resolução de Problemas como metodologia de ensino, é uma das formas mais acessíveis de proporcionar aos educandos a construção do conhecimento matemático.
Como metodologia para o ensino de Matemática, a Resolução de Problemas pode ser entendida como um “conjunto de procedimentos didáticos, representados por seus métodos e técnicas de ensino” (NÉRICE, 1987, p. 284), esse conjunto de métodos é utilizado com o intuito de alcançar objetivos de ensino e deve ser trabalhado com a:
[...] apresentação de situações abertas e sugestivas que exijam dos alunos uma atitude ativa ou um esforço para buscar suas próprias respostas, seu próprio conhecimento. O ensino baseado na solução de problemas pressupõe promover nos alunos o domínio de procedimentos, assim como a utilização dos conhecimentos disponíveis, para dar resposta a situações variáveis e diferentes (POZO; ECHEVERRÍA, 1988, p. 09).
O uso da Resolução de Problemas como metodologia de ensino requer do docente e dos discentes novas posturas e atitudes com relação ao trabalho nas aulas de Matemática, dentre essas características, Onuchic e Allevato (2004, p. 82) destacam que:
O professor precisa preparar, ou escolher, problemas apropriados ao conteúdo ou ao conceito que pretende construir. Precisa deixar de ser o centro das atividades, passando para os alunos a maior responsabilidade pela aprendizagem que pretendem atingir. Os alunos, por sua vez, devem entender e assumir essa responsabilidade. Esse ato exige de ambos, portanto, mudanças de atitude e postura, o que, nem sempre, é fácil conseguir.
No que se refere ao ensinar a resolver problemas, Pozo e Echeverría (1988, p. 14) acrescentam que não é suficiente “dotar os estudantes de habilidades e estratégias eficazes”, mas se faz necessário proporcionar a eles o hábito e a atitude de encarar a aprendizagem como um problema para o qual deve ser encontrada uma solução, ou seja, incentivar o educando a propor situações problema, partindo da realidade que o cerca, que merece dedicação e estudo. É preciso estimular nos estudantes o hábito pela problematização e a busca pelas respostas de suas próprias indagações e questionamentos, como forma de aprender.
Sendo assim, ao ensinar por meio da metodologia Resolução de Problemas, os estudantes podem desenvolver a capacidade de aprender a aprender sob uma perspectiva Freiriana, no tocante a indagações escolares ou cotidianas, ao invés de esperarem por uma resposta já pronta dada pelo docente ou pelo livro-texto.
Para entender o processo de elaboração de problemas para o cenário atual, a BNCC (BRASIL, 2018) orienta que os estudantes desenvolvam a capacidade de identificar oportunidades de utilização da Matemática para resolver problemas, aplicando conceitos, procedimentos e resultados para obter soluções e interpretá-las segundo os contextos das situações, utilizando a dedução de algumas propriedades e a verificação de conjecturas, a partir de outras.
Outro fator importante, que deve estar dentro do leque de preocupações dos professores durante o trabalho com a Resolução de Problemas, é se o estudante possui ou não pré-requisitos para a execução do problema proposto. Dentro dessa perspectiva, deve-se:
Propor aos estudantes várias estratégias de Resolução de Problemas, mostrando-lhes que não existe uma única estratégia, ideal e infalível. [...] A Resolução de Problemas não deve se constituir em experiências repetitivas, através da aplicação dos mesmos problemas (com outros números) resolvidos pelas mesmas estratégias. O interessante é resolver diferentes problemas com uma mesma estratégia e aplicar diferentes estratégias para resolver um mesmo problema. Isso facilitará a ação futura dos alunos diante de um problema novo (DANTE, 1991, p. 59).
O docente pode trabalhar com tentativas e erros dos estudantes, observando o caminho usado para chegar à solução do problema. Essa observação servirá para compreender o seu raciocínio e prepará-lo para as discussões em torno da resolução desses problemas, com o intuito de conceber os diferentes processos de resolução já aprendidos. O docente deve proporcionar aos estudantes:
O espírito solucionador, e a capacidade de resolver problemas deve incutir em suas mentes algum interesse por problemas e proporcionar-lhes muitas oportunidades de imitar e de praticar. Além disso, quando o professor resolve um problema em aula, deve dramatizar um pouco as suas ideias e fazer a si próprio as mesmas indagações que utiliza para ajudar os alunos. Por meio desta orientação, o estudante acabará por descobrir o uso correto das indagações e sugestões e, ao fazê-lo, adquirirá algo mais importante do que o simples conhecimento de um fato matemático qualquer (POLYA, 1995, p. 03).
Pressupondo que o discente incorpore e entenda a importância dessas indagações e recomendações, a fim de apoderar-se da disposição para resolver situações adversas, nesse caso, no âmbito do ensino da unidade temática Geometria, esta unidade:
[...] envolve o estudo de um amplo conjunto de conceitos e procedimentos necessários para resolver problemas do mundo físico e de diferentes áreas do conhecimento. Assim, nessa unidade temática, estudar posição e deslocamentos no espaço, formas e relações entre elementos de figuras planas e espaciais pode desenvolver o pensamento geométrico dos alunos. Esse pensamento é necessário para investigar propriedades, fazer conjecturas e produzir argumentos geométricos convincentes. [...] As ideias matemáticas fundamentais associadas a essa temática são, principalmente, construção, representação e interdependência (BRASIL, 2018, p. 271).
Antes de passar para etapas definidas por Polya (1995), é importante ressaltar que o sucesso dessas atividades dependerá do trabalho do professor a ser realizado em cada turma, considerando a habilidade de comunicação e a expressão oral e escrita, de cálculo e raciocínio lógico, favorecendo o desenvolvimento do pensar, do levar o educando a conhecer, questionar, transformar, produzir e compartilhar ideias.
A diretriz da BNCC (BRASIL, 2018) referente à Resolução de Problemas é determinada seguindo algumas concepções, determinadas nas competências específicas de linguagens para o ensino fundamental. Quando se trata do letramento matemático, os estudantes, ao trabalharem com a resolução de problemas, devem ter:
[...] competências e habilidades de raciocinar, representar, comunicar e argumentar matematicamente, de modo a favorecer o estabelecimento de conjecturas, a formulação e a resolução de problemas em uma variedade de contextos, utilizando conceitos, procedimentos, fatos e ferramentas matemáticas. É também o letramento matemático que assegura aos alunos reconhecer que os conhecimentos matemáticos são fundamentais para a compreensão e a atuação no mundo e perceber o caráter de jogo intelectual da matemática, como aspecto que favorece o desenvolvimento do raciocínio lógico e crítico, estimula a investigação e pode ser prazeroso (fruição) (BRASIL, 2018, p. 266).
Agora, quanto à competência específica 3, do Ensino Médio, que trata da Resolução de Problemas no ensino da Matemática, a BNCC espera que os educandos tenham competência de:
[...] identificar os conceitos e procedimentos matemáticos necessários ou os que possam ser utilizados na chamada formulação matemática do problema. Depois disso, eles precisam aplicar esses conceitos, executar procedimentos e, ao final, compatibilizar os resultados com o problema original, comunicando a solução aos colegas por meio de argumentação consistente e linguagem adequada, no entanto, a Resolução de Problemas pode exigir processos cognitivos diferentes. Há problemas nos quais os estudantes deverão aplicar de imediato um conceito ou um procedimento, tendo em vista que a tarefa solicitada está explícita. Há outras situações nas quais, embora essa tarefa esteja contida no enunciado, os estudantes deverão fazer algumas adaptações antes de aplicar o conceito que foi explicitado, exigindo, portanto, maior grau de interpretação (BRASIL, 2018, p. 535).
Para se resolver e encaminhar a resolução de um problema, Polya (1995) determina quatro etapas a serem seguidas:
1ª etapa – Compreensão do problema: nessa fase, o autor apresenta que, para compreender um problema, é necessário estimular o educando a fazer perguntas: O que é solicitado? Quais são os dados? Quais são as condições? É possível satisfazer as condições? Elas são suficientes ou não para determinar a solução? Faltam dados? Que relações podem ser estabelecidas para encontrar os dados omitidos? Que fórmulas e/ou algoritmos posso utilizar?
2ª etapa – Construção de uma resolução: momento para estimular os educandos a buscarem conexões entre os dados e o que é solicitado, estimulando, também, que pensem em situações similares, a fim de que possam estabelecer um plano de resolução, definindo prioridades e, se necessário, investigações complementares para resolver o problema.
3ª etapa – Execução escolhida: é o momento de executar o plano idealizado. Para que o educando obtenha sucesso, deve ser estimulado a realizar cada procedimento com muita atenção, estando atento a cada ação desenvolvida, verificando cada passo. O estudante também deve ser estimulado a mostrar que cada procedimento realizado está correto, possibilitando a afirmação de seu aprendizado e a comunicação de sua produção.
4ª etapa – Revisão da solução: é um momento muito importante, pois propicia uma depuração, é uma abstração da solução do problema. A depuração tem por objetivo verificar os procedimentos utilizados, procurando simplificá-los ou buscar outras maneiras de resolver o problema de forma mais simples. A abstração tem por finalidade refletir sobre o processo realizado, procurando descobrir a essência do problema e do método empregado para resolvê-lo, de modo a favorecer uma transposição do aprendizado adquirido nesse trabalho para a resolução de outras situações-problema.
Dentre algumas orientações de Dante (1991), a respeito do desenvolvimento de atividades em relação à Resolução de Problemas, uma delas é trabalhar com todos os estudantes de uma mesma turma, apresentando um problema desafiador, real e interessante, e que não seja resolvido diretamente por um ou mais algoritmos. O autor recomenda que seja dado um tempo razoável para que os educandos leiam e compreendam o problema.
Imaginando que a maioria dos estudantes solucionarão o problema, o próximo passo do docente é organizar a apresentação de todo o processo obtido no estudo para a sala de aula, explicando o que fizeram e como fizeram, e por que a sua estratégia funcionou ou não. O docente deverá registrar as sugestões dadas pelos educandos, pois é comum aparecerem modos diferentes de resolver o mesmo problema, e é interessante que todos sejam explorados, pois isso é uma maneira de incentivar o discente a sempre tentar vários métodos.
No âmbito do uso das Tecnologias da Informação e Comunicação como ferramentas para o aprendizado da Matemática, a escolha de um aplicativo torna-se um fator que determina a qualidade do aprendizado. A utilização de programas que oferecem recursos para a exploração de conceitos e de ideias matemáticas resulta em um importante uso de tecnologia para o ensino da Matemática. Referente às Tecnologias da Informação e Comunicação, temos que:
À medida que a tecnologia informática se desenvolve, nos deparamos com a necessidade de atualização de nossos conhecimentos sobre o conteúdo ao qual ela está sendo integrada. Ao utilizar uma calculadora ou um computador, um professor de matemática pode se deparar com a necessidade de expandir muitas de suas ideias matemáticas e também buscar novas opções de trabalho com os alunos (BORBA; PENTEADO, 2003, p. 64 - 65).
Pensando na importância das Tecnologias da Informação e Comunicação no ensino da matemática, foi que resolvemos utilizar a mediação tecnológica na proposta da atividade; no que se refere a essa abordagem, vemos as concepções de Giraldo et al. (2012), contemplando a existência de aplicativos, recursos ou ferramentas computacionais por meio dos quais os estudantes podem explorar e construir diferentes conceitos matemáticos, referidos como “programas de expressão”.
Cabe ainda destacar que a BNCC (BRASIL, 2018), entende que o uso de tecnologias possibilita aos estudantes experiências variadas e facilitadoras de aprendizagens que reforçam a capacidade de raciocinar logicamente, formular e testar conjecturas, avaliar a validade de raciocínios e construir argumentações. Atividades com lápis e papel, régua e compasso, se estimuladas pela tecnologia, poderão tornar-se fascinantes. Por exemplo, com o software GeoGebra, podem-se construir figuras geométricas com grande facilidade e rapidez.
Acerca das representações geométricas, Giraldo et al. (2012) defendem que o software GeoGebra inclui recursos de geometria, álgebra, tabelas, gráficos e cálculos simbólicos em um único ambiente. Para nossa proposta de atividade, podemos usufruir das construções geométricas por meio da utilização de pontos, retas, segmentos de reta, polígonos, entre outros, no software é possível modificar esses objetos dinamicamente, mesmo após a conclusão da construção.
O GeoGebra é um software dinâmico que apresenta aos discentes possibilidades de vivenciar processos criativos, estabelecer aproximações, juntar significados anteriormente desconexos e ampliar a capacidade de interlocução por meio das diferentes linguagens que tais recursos propiciam. A ideia é usar o GeoGebra para construir figuras geométricas, visualizar e explorar problemas encontrados pelos estudantes, momento que possibilitará o desenvolvimento de reflexões e conjecturas sobre os conceitos geométricos que serão estudados naquele momento.
Pensando dessa forma, é importante abordar o GeoGebra (4º etapa, revisão da solução) como ferramenta de ensino para o conteúdo matemático da atividade didática que será desenvolvida. O planejamento da atividade a seguir será analisado dentro da fundamentação teórica citada, em particular no trabalho de Polya (1995), que categoriza a Resolução de Problemas em etapas.
Essa proposta de atividade segue as concepções de Polya (1995), no tocante à metodologia Resolução de Problemas, e é mediada pelo software GeoGebra, apresentando uma situação problema envolvendo conceitos geométricos de congruência de triângulos. A atividade foi organizada para durar aproximadamente 2 horas.
A figura 1, a seguir, ilustra essa situação, que possui um segmento de reta (simbolizando o intervalo do rio) e dois pontos (cidades) distintos e não pertencentes ao segmento de reta.
Apresentamos a seguir os rocedimentos metodológicos.
O docente e os discentes medirão as dimensões da folha A4 com o uso da régua, aproximando os valores de comprimento e largura. O que é solicitado? O ponto em que será construída a ponte. Quais são as condições? Intervalo linear num certo percurso do rio, tal que uma ponte deve ser construída de modo a se gastar a menor quantidade possível de material em duas estradas que liguem a ponte a duas cidades, que estão localizadas na mesma margem. É possível satisfazer as condições, e elas são suficientes ou não para determinar a solução? “Sim”. Faltam dados? “Não”.
Após a descoberta dos dados e das relações, o docente volta a estimular os estudantes a buscarem conexões entre os dados e o que é solicitado, instigando-os. É o momento de o educando desenvolver um plano para procurar o melhor percurso (ter encontrado a estimativa da construção da ponte e seus comprimentos, como elaborar as estradas e mostrar o local exato da ponte) e pensar na estratégia para a execução do plano. Em seguida, pede-se aos educandos que façam uma representação gráfica da situação. Solicita-se que desenhem o rio sendo reta r e dois pontos representando as cidades A e B. Finalizada a discussão, o novo questionamento a ser resolvido é: onde deverá ser construída a ponte para que a soma das distâncias entre as cidades e a ponte seja mínima? O docente deve estimular os discentes a refletirem sobre a distância possível, para que a construção gaste a menor quantidade de materiais.
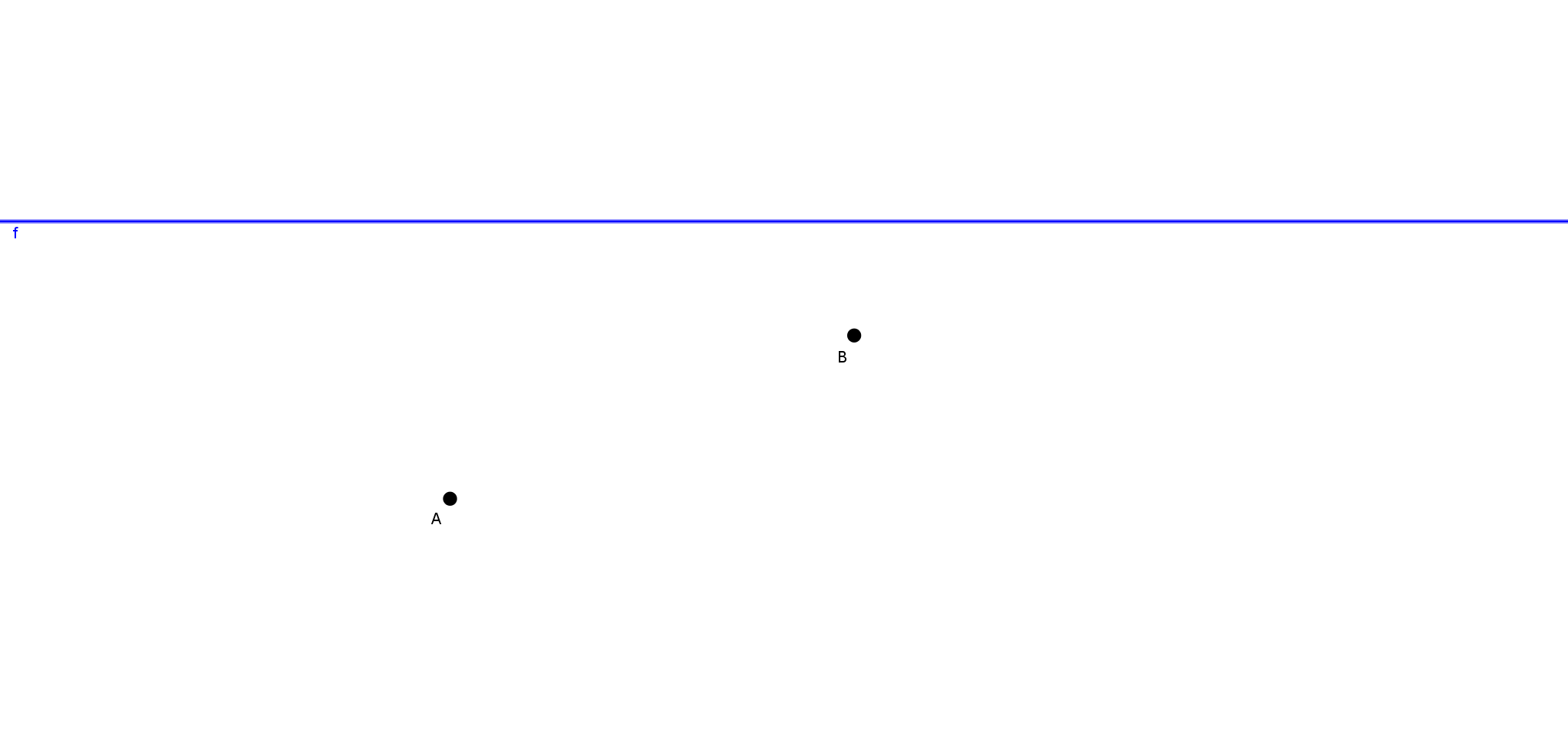
Após ter o plano em mãos, o docente poderá observar as concepções dos educandos frente à demonstração. Executar um plano: Esboçar uma reflexão de uma das cidades em relação à reta r, que representa o rio. Chamar a cidade B de ponto B, sua reflexão em relação à reta r de ponto B’, e a cidade A de ponto A. Quando refletimos o ponto B, em relação à reta r, o segmento BB’ forma um ângulo de 90° no ponto O, que pertence à reta r, e os segmentos BO e OB’ serão equivalentes, de fato, pois o segmento OB’ é reflexo do segmento BO. A partir daí, construir os segmentos AB’ e BE, sendo E o ponto de intersecção entre o segmento AB’ e a reta r.
Logo, pelo caso de congruência lado, ângulo e lado (LAL), os triângulos BOE e B’OE são congruentes. De fato, pois o segmento OE é comum a ambos os triângulos, BÔE B’ÔE 90º e BO OB’ (o símbolo significa congruência). Então, BE B’E.
Sabendo que o segmento AB’ é a menor distância entre os pontos A e B’ (pois na Geometria Euclidiana a menor distância entre os pontos A e B’ distintos é o segmento de reta cujas extremidades são os pontos A e B’) e que BE B’E, segue que AB’ = AE + EB’ = AE + EB, como AB’ é a menor distância, tem-se que AE + EB é a menor distância, logo, o ponto E ilustrado a seguir na Figura 2 é o local onde a ponte deverá ser construída.
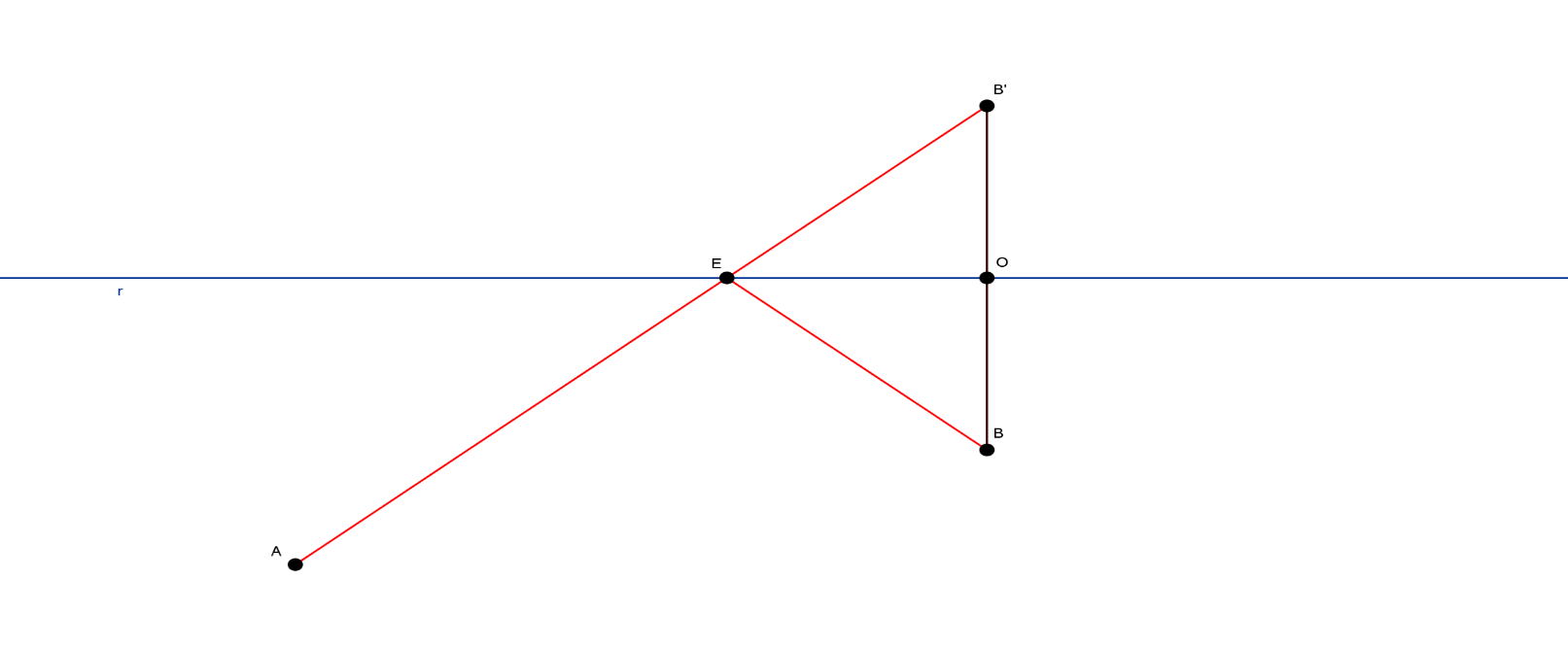
Assim, juntamente com os educandos, é preciso chegar a uma forma conceitual de resolver o problema pelo experimento em discussão, usando a Geometria Euclidiana como alicerce.
Utilizar como ferramenta o GeoGebra, como um teste prático alternativo para concluir de fato se o Ponto E é correspondente à resposta adequada. Dever-se-á encontrar a melhor posição para minimizar os custos da construção. Para isso, uma sugestão é o procedimento descrito:
1) Construa uma reta r (rio) e os pontos A (cidade A) e B (cidade B), como na Figura 1.
Passo 1: Abra o aplicativo GeoGebra;
Passo 2: Ative a ferramenta reta (na janela 3) e crie uma reta r;
Passo 3: Ative a ferramenta pontos (na janela 2) e crie um ponto A e o ponto B;
2) Construa um ponto E, pertencente ao r, e os segmentos AE e BE, como na figura 3.
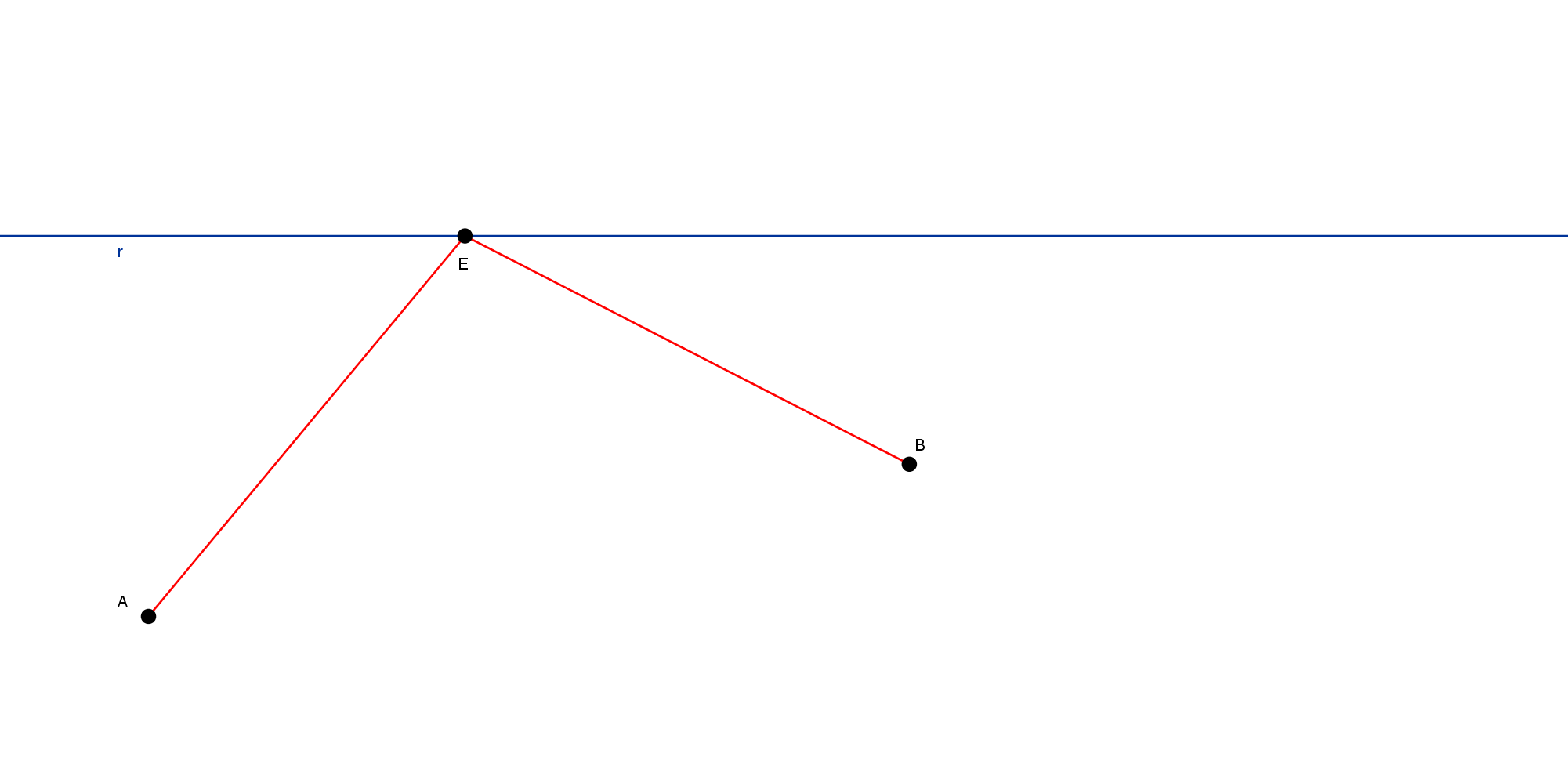
Passo 1: Ative a ferramenta pontos (na janela 2), crie o ponto E, pertencente à reta r;
Passo 2: Ative a ferramenta segmento (na janela 3), crie o segmento AE e o segmento BE;
3) Calcule o comprimento dos segmentos AE e BE.
Passo 1: Ative a ferramenta “Distância, Comprimento ou Perímetro” (janela 8) e calcule a distância dos segmentos AE e BE;
Passo 2: Clique com o botão esquerdo do mouse nos segmentos AE e BE;
4) Movimentar o Ponto E sobre a reta r.
Passo 1: Ative a ferramenta mover (janela 1) e movimente o ponto E sobre a reta r;
5) Analisar a soma dos comprimentos de AE e BE ao movimentar o ponto E sobre a reta r. O menor comprimento d = AE + BE é o local onde a ponte será construída, pois terá menor distância.
Terminado a experiência, os educandos terão uma estimativa sobre o ponto onde a soma das distâncias é mínima, isto é, um local para a construção da ponte.
Conclusão (duração: 10 minutos): Momento para uma breve revisão do que foi ensinado e praticado por meio do da resolução do problema.
Avaliação: Observar o envolvimento dos estudantes, de forma individual e coletivamente, acerca dos processos solicitados, analisando o trabalho executado, comparar esse resultado com outros e, ainda, tentar prever o potencial de crescimento de cada estudante. Verificar motivação e empenho na execução das atividades e no desenvolvimento de atitudes na interação, cooperação e organização. E, com isso, verificar se foram alcançados os objetivos estabelecidos inicialmente.
Os educandos, ao participarem da atividade que o docente orientará com o intermédio do projetor, poderão descobrir fatos novos, sendo, assim, incentivados a encontrarem outras maneiras de resolverem o problema, despertando a curiosidade e o interesse pelos conhecimentos matemáticos e, desse modo, desenvolvendo a capacidade de solucionar situações-problemas que lhes são propostas.
Assim, despertar no educando o gosto pela resolução de problemas não deve ser tarefa fácil, muitos são os momentos de dificuldades e de obstáculos. Isso pode acontecer devido aos docentes e educandos não conseguirem distinguir um problema matemático de um exercício matemático.
Ao analisamos esta proposta de atividade, devemos estabelecer relações, de acordo com as perspectivas de seus passos. A etapa de compreensão do problema foi construída de forma a entender o problema, sendo necessário estimular e fazer perguntas. Nesse processo, torna-se necessário construir figuras para esquematizar a situação, destacando valores, correspondências e usos da notação matemática.
Na construção de uma resolução, é preciso estimular a busca por conexões entre os dados e o que é solicitado, estimulando os alunos a pensarem em situações similares, a fim de que possam estabelecer um plano de resolução. Já na execução da resolução escolhida, são desenvolvidos os conceitos geométricos de forma lógica e analítica, pois, para alcançar o objetivo da situação, é preciso raciocínio matemático adequado e, sobretudo, de ter conhecimento referente à congruência de triângulos.
Já na revisão da solução, usamos o software GeoGebra, que, segundo Giraldo et al. (2012), é uma ferramenta que proporciona a exploração e a construção de diferentes conceitos matemáticos, pois nessa etapa se faz necessário realizar experimento no qual os educandos devem ter a oportunidade de “observar” de fato o resultado do problema, de forma empírica; no nosso caso, utilizamos a tecnologia. Assim, essa ferramenta deixa prática a abstração e, com isso, a aproxima da realidade.
Esse modo de ensinar poderá aguçar as habilidades dos educandos, proporcionando a explicação e o entendimento de lidar com a realidade do problema e, assim, colocá-los em desafios que exigem dedicação. Ao proporcionar esse tipo de atividade aos educandos, é possibilitada a ampliação do conhecimento, o desenvolvimento do raciocínio lógico e o enfrentamento de novas situações. Portanto, essa proposta poderá sanar as dificuldades encontradas em sala de aula, oferecendo aos professores soluções didáticas para o ensino de geometria via metodologia Resolução de Problemas, mediada pelo GeoGebra.
Diante dos estudos de Onuchic (2013), destaca-se a importância de se trabalhar, no processo de ensino e aprendizagem, a Resolução de Problemas para o desenvolvimento intelectual do estudante. Os professores são fundamentais no ato de aprender e devem propor atividades que despertem o entusiasmo, desenvolvendo, assim, a capacidade dos educandos, dentro dos aspectos da criação, da atuação em conjunto, aproximando-os uns dos outros, demonstrando a importância de cada um.
Desenvolver a capacidade de resolver problemas e ter a Resolução de Problemas como ponto de partida fundamental da atividade matemática são finalidades e orientações da BNCC (BRASIL, 2018), que visam construir referências nacionais comuns ao processo educativo, para que os discentes possam ter acesso ao conjunto de conhecimentos necessários ao exercício da cidadania.
Esta pesquisa assumiu como tema central a utilização da Resolução de Problemas na prática educativa da matemática como uma metodologia de ensino, teve como objetivos elaborar uma revisão bibliográfica sobre a metodologia Resolução de Problemas e oferecer aos professores da educação básica uma proposta de atividade para o ensino de conceitos da unidade temática Geometria, mediada por ferramenta tecnológica (software GeoGebra).
Os autores Borba e Penteado (2003), Dante (2003), Firer (2011), Grando (2000), Polya (1995), Pozo e Echeverría (1998) contribuíram para a exploração teórica do assunto em tela, cujos dados empíricos foram obtidos por meio de uma abordagem qualitativa, amparada por eixos categorizados sobre a metodologia de ensino Resolução de Problemas, assim, construímos uma proposta de atividade que trata desse contexto. Então, a análise da proposta orienta que não se pode mecanizar o ensino e que a aprendizagem por intermédio das ferramentas tecnológicas pode se tornar eficiente, caso educandos e professores se empenhem na construção do referido processo educativo, possibilitando também o gosto pelo raciocínio matemático.
Não se aplica.
Não houve financiamento.
Resumo/Abstract/Resumen: Vilmar Costa Silva e Ivo Pereira da Silva.
Introdução: Vilmar Costa Silva e Ivo Pereira da Silva.
Referencial teórico: Vilmar Costa Silva e Ivo Pereira da Silva.
Análise de dados: Vilmar Costa Silva e Ivo Pereira da Silva.
Discussão dos resultados: Vilmar Costa Silva e Ivo Pereira da Silva.
Conclusão e considerações finais: Vilmar Costa Silva e Ivo Pereira da Silva.
Referências: Vilmar Costa Silva e Ivo Pereira da Silva.
Revisão do manuscrito: Layssa de Jesus Alves Duarte
Aprovação da versão final publicada: Vilmar Costa Silva e Ivo Pereira da Silva.
Os autores declararam não haver nenhum conflito de interesse de ordem pessoal, comercial, acadêmico, político e financeiro referente a este manuscrito.
Os autores declararam que disponibilizam os dados da pesquisa.
Não se aplica.
Não se aplica.
SILVA, Vilmar Costa; SILVA, Ivo Pereira da. Ensino de congruência de triângulos: Resolução de problemas mediada pelo software GeoGebra. REAMEC – Rede Amazônica de Educação em Ciências e Matemática. Cuiabá, v. 9, n. 2, e21041, maio a agosto, 2021. https://doi.org/10.26571/reamec.v9i2.12162
Silva, V. C.; Silva, I. P. (2021). Ensino de congruência de triângulos: Resolução de problemas mediada pelo software GeoGebra. REAMEC - Rede Amazônica de Educação em Ciências e Matemática, 9 (2), e21041. https://doi.org/10.26571/reamec.v9i2.12162
Licenciado sob a Licença Creative Commons Attribution-NonCommercial 4.0 International (CC BY-NC 4.0). Esta licença permite compartilhar, copiar, redistribuir o manuscrito em qualquer meio ou formato. Além disso, permite adaptar, remixar, transformar e construir sobre o material, desde que seja atribuído o devido crédito de autoria e publicação inicial neste periódico.
Os direitos autorais são mantidos pelos autores, os quais concedem à Revista REAMEC – Rede Amazônica de Educação em Ciências e Matemática - os direitos exclusivos de primeira publicação. Os autores não serão remunerados pela publicação de trabalhos neste periódico. Os autores têm autorização para assumir contratos adicionais separadamente, para distribuição não exclusiva da versão do trabalho publicada neste periódico (ex.: publicar em repositório institucional, em site pessoal, publicar uma tradução, ou como capítulo de livro), com reconhecimento de autoria e publicação inicial neste periódico. Os editores da Revista têm o direito de proceder a ajustes textuais e de adequação às normas da publicação.
Universidade Federal de Mato Grosso. Programa de Pós-graduação em Educação em Ciências e Matemática (PPGECEM) da Rede Amazônica de Educação em Ciências e Matemática (REAMEC). Publicação no Portal de Periódicos UFMT. As ideias expressadas neste artigo são de responsabilidade de seus autores, não representando, necessariamente, a opinião dos editores ou da referida universidade.
Dailson Evangelista Costa
Orcid:https://orcid.org/0000-0001-6068-7121
Lattes:http://lattes.cnpq.br/9559913886306408
https://periodicoscientificos.ufmt.br/ojs/index.php/reamec/article/view/12162 (pdf)





