



Artigos
RECURSO DIDÁTICO PARA ENSINAR GEOMETRIA: O USO DE DOBRAS DE PAPEL PARA OBTER REGIÕES POLIGONAIS/POLÍGONOS
DIDACTIC RESOURCE TO TEACH GEOMETRY: THE USE OF FOLDS OF PAPER TO OBTAIN POLYGONAL REGIONS/POLYGONS
REAMEC – Rede Amazônica de Educação em Ciências e Matemática
Universidade Federal de Mato Grosso, Brasil
ISSN-e: 2318-6674
Periodicidade: Frecuencia continua
vol. 5, núm. 2, 2017
Recepção: 09 Outubro 2017
Aprovação: 16 Novembro 2017

Resumo: Neste artigo, apresentam-se alguns resultados de uma pesquisa qualitativa, realizada pelo Grupo de Estudos e Pesquisas em Geometria-GEPGEO, que teve por objetivo explorar o recurso didático papel, por meio de dobraduras específicas na dinamização de atividades exploratórias em representações de regiões poligonais/polígonos, visualmente regulares, de 3 a 11 lados. Foram desenvolvidas atividades investigativas, com o intuito de obter dimensões das faixas de papel, que gerariam regiões poligonais com aproximadamente a mesma área, ou seja, polígonos inscritos em circunferências de mesmo raio. Além disso, investigou-se o tipo de material que mais se adequou às construções e à manipulação de modo a obter as figuras geométricas visual e esteticamente adequadas. Concluiu-se que os objetos construídos com papel pardo favoreceram a visualização, a identificação dos elementos das figuras e baixo custo de produção. Por meio de experimentação e por cálculos matemáticos, obteve-se as melhores medidas de lados dos polígonos/regiões poligonais em cada caso. Espera-se que esse estudo possa contribuir para a sala de aula na escola básica.
Palavras-chave: dobraduras, materiais manipuláveis, recursos didáticos, ensino de geometria.
Abstract: This paper, it presents some results of a qualitative research carried out by the Group of Studies and Research in Geometry-GEPGEO, whose objective was to explore the resource didactic paper, through specific folding in the dynamization of exploratory activities in polygonal regions/polygons, visually regular, from 3 to 11 sides. Research activities were carried out in order to obtain dimensions of the paper strips, which would generate polygonal regions with approximately the same area, that is, polygons inscribed in circumferences of the same radius. In addition, it was investigated the type of material that best suited the constructions and the manipulation in order to obtain the visual and aesthetically adequate geometric figures. It was concluded that the objects constructed with brown paper favored the visualization, the identification of the elements of the figures and the low cost of production. Throughout experimentation and mathematical calculations, the best measurements of sides of the polygons / polygonal regions were obtained in each case. It is hoped that this study will contribute to the classroom in Elementary School.
Keywords: folders, manipulative materials, didactic resources, geometry teaching.
1. CONTEXTUALIZANDO A PESQUISA: O GEPGEO E OS MATERIAIS MANIPULÁVEIS
O Grupo de Estudos e Pesquisas em Geometria – GEPGEO, foi constituído junto a um programa de pós-graduação, envolvendo alunos de mestrado e doutorado bem como ex-alunos desse programa que estão atuando nas redes de ensino privado e público, sendo aberto a outros participantes interessados pela área. No ano de 2017 os estudos e pesquisas estão se desenvolvendo com o tema materiais manipuláveis, os quais recebem diversas conotações, como se explana a seguir.
Dienes e Golding (1977) encaminham alguns tipos de jogos que podem ser empregados na determinação de atributos que conduzem a conceitos geométricos, em particular. Um exemplo dado pelos autores, que pode ser utilizado com crianças bem pequenas, já na pré-escola, levando à compreensão de conceitos de longo, curto, rugoso, liso, grande, pequeno, reto, torto, pontudo, rombo, redondo, dentre outros, consiste em dispor objetos de diversos tamanhos, formas, rugosidade, em um compartimento qualquer, e pedir, individualmente, que entreguem ao professor o(s) objeto (s) com dados atributos escolhidos por ele. Pode, além disso, pedir que sejam feitas representações de objetos solicitados. Outros jogos podem explorar formas, cores, relações espaciais simples como os objetos que rolam e os que não rolam. Todo este manuseio de materiais concretos pode estimular o interesse inicial da criança pela visualização geométrica. As noções topológicas elementares, por independerem de medida, são fundamentais de serem trabalhadas nessa fase infantil.
A investigação, realizada por Oliveira e Leivas (2017), teve por objetivo desenvolver percepção visual com estudantes de quinto ano do Ensino Fundamental, com base na teoria de van Hiele, utilizando material concreto, similarmente ao feito por Dienes e Golding (1975). Nela foi utilizada uma caixa opaca, com objetos de diversas formas e tamanhos, tendo um orifício no qual o estudante introduzia uma mão e utilizava o tato para descrever um objeto e tentar identificá-lo de forma verbal para o grupo de alunos, indicando propriedades e componentes, nomeando-os para, posteriormente, representá-lo. Assim, desenvolveram visualização, como construto mental, de formas espaciais que se encontravam na caixa, num procedimento didático que conduziu à aquisição de conhecimentos dos envolvidos pelo uso de recursos materiais.
Um dos objetivos da didática, preconizado por Pais (2001), consiste em distinguir conhecimento de saber. Enquanto o saber científico se encontra mais no contexto acadêmico, o conhecimento é considerado mais aproximado da cognição, ou seja, [...] “o conhecimento refere-se mais à dimensão individual e subjetiva, revelando algum aspecto com o qual o sujeito tenha uma experiência direta. Nessa concepção, está mais presente o caráter experimental e pragmático do que o aspecto teórico e racional” (p. 36-37). O GEPGEO entende, nesse momento, que explorar recursos didáticos, materiais manipuláveis ou outro codinome que se lhe atribua, se faz importante na construção do conhecimento geométrico. Mas qual ou quais são os significados dessas palavras? No que segue apresenta-se alguns significados, comparativos e distinções a partir do estudo realizado por Botas e Moreira (2013).
Para as autoras, materiais didáticos e materiais manipuláveis são caracterizados por Zabala (1998, apud BOTAS e MOREIRA, 2013) como materiais curriculares, ou seja, são meios que ajudam a responder aos problemas concretos que as diferentes fases do processo de planejamento, execução e avaliação lhes apresentam, utilizados pelo professor para o desenvolvimento de unidades didáticas. Eles possuem a função de orientar, guiar, exemplificar, ilustrar, propor, divulgar. Estão relacionados com o ensino e a aprendizagem ao nível individual e têm a intencionalidade de englobar os materiais de acordo com sua função e propósito a fim de guiar, exemplificar, ilustrar, divulgar conteúdos matemáticos. Como suporte reúnem o papel, a projeção em movimento, dentre outros, sempre ligados a conteúdos procedimentais.
Segundo as autoras, para Graells (2000, apud BOTAS e MOREIRA, 2013), os recursos educativos são quase todos aqueles que podem facilitar a aprendizagem, quando utilizados num contexto de formação específica. São tipo convencionais, audiovisuais, tecnológicos e apresentam a função de fornecer informação, constituir guias da aprendizagem, proporcionar treinos e exercitar capacidades, cativar interesse e motivar, avaliar capacidades e conhecimentos, proporcionar simulações. Por sua vez, indicam que para Chamorro (2003, apud BOTAS e MOREIRA, 2013), eles são todos os meios que o professor pode utilizar para ensinar o que condiz com as concepções de Zabala e Graells. Indo mais além, são todos os que podem ser manipulados e trabalhados de forma a permitir obter resultados finais relevantes à atividade em sala de aula, dando atribuição intuitiva a nomes e conceitos dos objetos matemáticos de forma a favorecer a comunicação na relação professor/aluno.
Botas e Moreira (2013) indicam que, para Mansutti (1993), o material didático ou instrucional é um recurso utilizado durante uma ação do professor em que se conjuga aprendizagem e a formação, enquanto para Ribeiro (1995), o material manipulável é qualquer objeto concreto que incorpora conceitos matemáticos, apela a diferentes sentidos, podendo ser tocado, rearranjado e manipulados pelas crianças. Para esse autor, material didático é qualquer recurso utilizado na sala de aula tendo como objetivo promover a aprendizagem.
A partir dessa análise feita por Botas e Moreira (2013) se conclui que materiais didáticos são recursos materiais manipuláveis, calculadoras, manuais escolares, fichas ou guias de grupo e outros mais, que possibilitam ao professor desenvolver um ensino centrado no aluno e na sala de aula e que auxiliem a aprendizagem, desenvolvendo uma atitude positiva dos alunos face à Matemática.
Como conclusão do levantamento bibliográfico realizado pelo GEPGEO, elaborou-se a seguinte definição para recursos didáticos ou manipuláveis: são todos os recursos materiais que podem ser utilizados pelo professor, de forma intencional, explorados pelos estudantes e que propiciem a construção do conhecimento, por exemplo, softwares dinâmicos, jogos, os de uso comum como sólidos geométricos, geoplanos ou blocos multibásicos.
A partir dessa conceituação sobre o tema, levantou-se a seguinte questão de pesquisa: como dinamizar a exploração do recurso didático papel, por meio de dobraduras específicas, para obter representações de regiões poligonais/polígonos, visualmente regulares[5], de 3 até 11 lados? Na busca de resposta a essa questão delineou-se o objetivo: investigar maneiras de dinamizar atividades exploratórias em representações de regiões poligonais/polígonos, visualmente regulares, de 3 até 11 lados.
A partir da questão de pesquisa, o GEPGEO busca a melhoria pedagógica de professores e futuros professores; desenvolver um grupo auto-reflexivo para atuação na escola; estudar alternativas de melhoria das condições de um trabalho pedagógico investigativo.
2. O PERCURSO DA INVESTIGAÇÃO
Partindo de um trabalho teórico (MIRANDA,1993), que indicava o uso de papel e dobras como recurso para construção de polígonos, compreende-se que o presente trabalho se caracteriza como uma pesquisa-ação, segundo Fiorentini e Lorenzato (2006) e, nessa linha, o grupo, constituído de dez participantes, iniciou a pesquisa.
Nesse sentido entende-se que foi feita uma pesquisa de cunho qualitativo interpretativo, uma vez que para Moreira (2011, p. 76): “O interesse central dessa pesquisa está em uma interpretação dos significados atribuídos pelos sujeitos à suas ações em uma realidade socialmente construída, através de observação participativa, isto é, o pesquisador fica imerso no fenômeno de interesse” (grifo do autor).
Miranda (1993) não explicita o tipo de papel empregado e nem dimensões das tiras. Partiu-se, inicialmente, para investigar o tipo de material que mais se adequava para a exploração das dobraduras. A Figura 1 ilustra o primeiro material empregado, utilizado por costureiras, em diversas larguras e cores.

Este material tem facilidade de marcar bem as dobras, entretanto, os vincos não se destacam no colorido da fita. Na Figura 2, ilustra-se a construção de um triângulo equilátero em papel dupla face, tipo laminado, o qual tem uma vantagem acentuada em relação ao anterior por destacar o triângulo (em verde). Observa-se que, na busca do triângulo equilátero, a dobra deve sobrepor-se ao lado adjacente ao triângulo.

Na busca de melhor visualização da figura, constatou-se que a percepção visual mais adequada ocorre quando se toma uma tira com, aproximadamente, 5 cm de largura sendo necessário um comprimento de 10 cm a fim de que fiquem sobras para seu manuseio. As investigações levaram ao questionamento de qual seria a largura e o comprimento adequados para que as diversas regiões poligonais tivessem áreas muito aproximadas, o que é objeto principal deste artigo. Assim, algumas questões foram elencadas: se mantiver a largura da fita o lado do polígono se mantém o mesmo? A área aumenta, diminui ou se mantem? Na Figura 3 se ilustra regiões poligonais e suas fronteiras no referido papel, obtidos com uma única tira.

A Figuras 4 ilustra o uso de dobras em papel ofício comum, com a marcação das dobras feitas com canetas coloridas, indicando os polígonos resultantes. A primeira é um pentágono feito com uma única tira e a segunda, com duas tiras, fornece o hexágono. Conclui-se que este material é o mais econômico, podendo ser aproveitadas folhas já usadas e disponíveis no ambiente escolar

O material utilizado nas construções da Figura 5 parece ter sido o segundo melhor adaptado, uma vez que ele permite a visualização das dobras, mesmos ocultas, quando colocado sob uma fonte luminosa, o que favorece a observação das diagonais dos polígonos. Observa-se que ele é facilmente dobrável, tanto quando se utiliza uma tira para os polígonos de número de lados ímpares, quando duas tiras, para os de lados pares.

Nessa fase da investigação, com os diversos tipos de materiais empregados, foram feitas várias sínteses preliminares e questionamentos para investigar, como se observa na Figura 6. Nela se identifica que, para a obtenção dos polígonos com número de lados ímpares, é utilizada uma única tira ou faixa enquanto que para os pares são necessárias duas tiras.

Na busca do papel que melhor se adequasse às investigações, encontrou-se o que ilustra a próxima sequência, Figura 7, do tipo pardo que se encontra no comércio, a baixo custo, e adquirido por metro linear. Na figura, da direita para a esquerda, regiões poligonais/polígonos de 3,5,7,9,11 lados, construídos com uma tira.

No que segue se ilustra a sequência da construção do triângulo equilátero com esse material, que foi o escolhido pelo grupo para as demais construções.

Tomada a decisão sobre o material que melhor se adequasse ao trabalho, o próximo passo foi investigar o comprimento das fitas necessário para se obter figuras de tamanhos aproximados, ou seja, de áreas aproximadamente equivalentes. Isso exigiu um estudo aprofundado das relações matemáticas envolvidas para além da percepção visual intuitiva o que vai ao encontro do que Fischbein (1987), indicou sobre afirmações auto evidentes, e o que entende Gategno (apud SABBATIELLO, 1967)(a respeito do que pode oferecer o recurso material. Com isso, busca-se ir além da percepção, do conhecimento imediato, adquiridos no manuseio e exploração dos diversos papeis encontrados no mercado para uma comprovação matemática de relações geométricas. Nesse sentido, o nível 1 da teoria de van Hiele, que estabelece o reconhecimento ou visualização de um objeto por sua aparência global fica perfeitamente caracterizado com este tipo de atividade e material.
Uma segunda decisão tomada foi, primeiramente, trabalhar com uma única tira, a qual permite a construção de regiões poligonais/polígonos com número ímpar de lados, o que consta do presente artigo, juntamente com o cálculo indicado no parágrafo anterior. Posteriormente, o grupo desenvolveu atividades exploratórias com duas tiras, as quais produzem regiões poligonais/polígonos com número para de lados.
Na determinação dos valores dos lados para que os polígonos estejam inscritos numa mesma circunferência de raio r, é necessário encontrar uma relação do comprimento do lado l em função de r. Desse modo, supõe-se um polígono qualquer e suas respectivas características, como o da Figura 10 (particularizada pelo pentágono inscrito numa circunferência de raio r), mas que deve considerar-se com polígono qualquer de n lados.
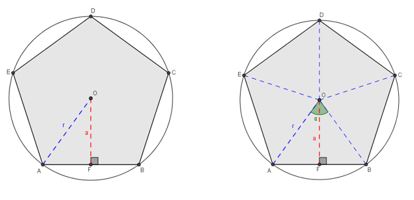
Em um polígono qualquer de n lados, inscrito numa circunferência de raio r, a distância que une qualquer vértice ao centro O da circunferência, é igual a r e a distância OF, pertencente à mediatriz do segmento AB, é o apótema (a) do polígono. Assim, ao unir os raios aos vértices do polígono, formam-se n ângulos centrais, cujos lados são dois raios consecutivos e, portanto, cada um valendo 360º/n.
Seja o polígono AOF um triângulo retângulo em F, no qual AO=r, FO=a e AF, que é determinada pela mediatriz de AB, com AF = l/2. Do mesmo modo que a mediatriz de AB define AF, a bissetriz de AOB determina AOF = α/2 (Figura 11), da qual se obtém a relação:
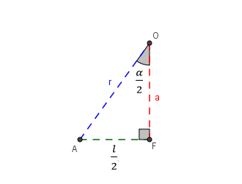
sen(α/2)= l/2r (1)
Substituindo-se o valor de α=360°/n em (1), segue que
sen(180°/n)= l/2r (2)
Assim, l=2r.sen(180°/n) (3)
A equação (3) corresponde à função desejada inicialmente e expressa l em função de r. Portanto, é possível obter um valor real para r que corresponda ao raio de todos os polígonos a serem construídos. Os experimentos realizados pelo grupo recomendam o comprimento da fita ideal para a construção do undecágono como sendo de 150 cm, o que conduz à medida do lado de l11=3 cm (4)
Ao substituir (4) em (3), se obtém r ≅ 5,3 cm (5)
Isso corresponde à medida do raio de circunscrição para todos os polígonos. Substituindo (5) em (3), tem-se a função geradora das demais medidas de ln, de acordo com seu número de lados.
l=10,6.sen(180°/n). (6)
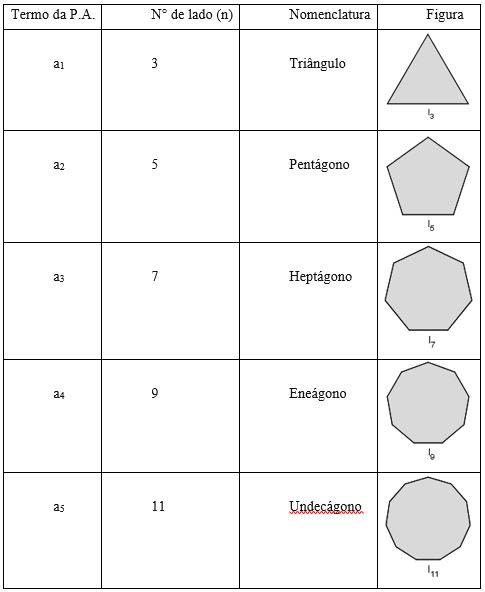
O Quadro 2 se refere às medidas dos lados dos polígonos de n lados, com n natural, ímpar e menor ou igual a onze, inscritos na circunferência de raio r ≅ 5,3 cm, a partir do que são construídos os outros polígonos por dobradura.
| Polígono | Medida do lado (ln) aproximado | Comprimento |
| Triângulo | l3 ≅ 9,2 cm | 30 cm |
| Pentágono | l 5 ≅ 6,2 cm | 50 cm |
| Heptágono | l 7 ≅ 4,6 cm | 100 cm |
| Eneágono | l 9 ≅ 3,6 cm | 140 cm |
| Undecágono | l l1=3 cm | 150 cm |
No que segue se apresenta uma descrição sucinta dessas construções.
Para fazer o triângulo utiliza-se uma faixa de papel pardo de 9,2 cm da largura por 30 cm de comprimento. Uma das extremidades deve passar por baixo e a outra por cima, ajustando-se com o ato de puxar as extremidades até acertar para que as dobras demarquem os lados de um triângulo (Figura 9). Pode se marcar tais linhas de dobra contornando-as com uma caneta hidrocor (Figura 4) ou esconder as partes excedentes por detrás do triângulo, deixando-o em destaque. Tenta-se ajustar para que visualmente se assemelhe a um triângulo equilátero, de modo que a largura da faixa encaixe no comprimento obtendo um triângulo com as mesmas dimensões de lado. Um dos lados fica demarcado pela dobra e os outros sem o excesso de papel, como foi representado na sequência da Figura 9.
Para a construção do pentágono, tomou-se uma faixa de 6,2 cm de largura por 50 cm de comprimento. Dá-se uma laçada, ajusta-se e puxa-se as extremidades de modo que fique com os lados visualmente congruentes. Essa ideia intuitiva do polígono regular necessita de comprovação matemática, no entanto se corrobora o dito por Fischbein (1987) a respeito de que a auto evidência deve ultrapassar os fatos observados e ir ao encontro do conhecimento formal. O material didático construído proporciona tal aquisição segundo a investigação realizada pelo GEPGEO. Nessa situação utilizou-se a largura da faixa de 6,2 cm, menor do que no caso do triângulo, porém o comprimento necessário aumentou, necessitando, agora, de 50 cm. A Figura 12 fornece a sequência para a obtenção do pentágono.

Na construção da região poligonal de sete lados com, aproximadamente, a mesma área das anteriores, com mesma medida do raio da circunferência circunscrita da figura ao pentágono, utilizou-se uma faixa de 4,6 cm de largura por 100 cm de comprimento. O comprimento aumenta consideravelmente em função de ser necessário dar duas voltas, por dentro, como se fosse dar um nó na tira, ao contrário das situações anteriores e, posteriormente, realizar o ajuste das pontas. Há uma dificuldade crescente em relação aos dois casos precedentes, exatamente na tentativa de ajuste para a obtenção do hexágono visualmente regular. Ao esconder os excessos nas extremidades a figura geométrica se torna mais evidenciada.
Para a construção do eneágono utilizou-se uma faixa de 3,6 cm de largura e 140 cm de comprimento, com procedimento semelhante à construção anterior, sendo agora necessárias três voltas. O detalhe a considerar aqui é tentar segurar no meio da faixa pelo comprimento, aonde elas se separam em duas, isto é, no ponto em que se dividem as voltas de cima e as de baixo. Ao firmar a faixa ao meio ela não escapa e se consegue visualizar para onde estão indo as extremidades e qual dever ser puxada, como pode ser vista na Figura 13.

Na última construção realizada com o material papel, usando a metodologia aqui empregada, a do undecágono, polígono de onze lados, considerou-se a tira com 3 cm de largura e 150 cm de comprimento. Inicia-se o processo por uma das extremidades, dá-se uma primeira volta, formando o pentágono. Ao dar a segunda volta se forma o heptágono e, na terceira, constitui-se o eneágono para, em uma quarta, finalizar a obtenção do undecágono. Basta fazer os ajustes, pois se espera já terem sido adquiridas habilidades motoras nas construções anteriores (Figura 14).

3. CONCLUINDO, MAS NÃO FINALIZANDO
O presente artigo apresentou parte de uma pesquisa em desenvolvimento, que buscou viabilizar a utilização do papel como recurso didático na construção de regiões poligonais/polígonos, visualmente regulares, com número de lados ímpares variando de 3 até 11.
O trabalho, envolvendo um grupo de estudos e pesquisas em Geometria, averiguou qual o material mais apropriado para a realização das dobras, tendo concluído que o papel pardo se tornou o mais adequado, especialmente para as escolas básicas, por ser um recurso de baixo custo e por favorecer a visualização das linhas de dobra, além de poder ser adquirido no comprimento desejado sem necessidade de emendas ou colagens.
Buscou-se, inicialmente, a partir da conceituação sobre materiais manipuláveis, o que a literatura apresentava para, então, investigar formas de dinamizar atividades exploratórias em representações de regiões poligonais/polígonos, visualmente regulares, de 3 até 11 lados. Para tal, referenciando as construções apresentadas neste artigo, compreende-se que o objetivo foi alcançado.
Além disso, foi destacada a busca para encontrar figuras que apresentassem uma estética visual adequada, de modo que todas tivessem aproximadamente a mesma área. Para tal, foi investigado o raio de uma circunferência circunscrita a tais figuras, relacionados ao lado das mesmas. Após a exploração de diversos materiais nas construções e de cálculos experimentais e matemáticos, chegou-se a um consenso de qual seria a melhor largura das faixas a serem dobradas, bem como os comprimentos necessários a fim de que não houvesse colagens, o que dificulta tanto as dobras quanto a estética.
Dessa forma, crê-se que a questão norteadora deste trabalho foi respondida e, em próxima produção, se irá apresentar o caso de regiões poligonais/polígonos com número de lados pares, o que já foi concluído. Por fim, espera-se que esse estudo possa trazer contribuições para a sala de aula na escola básica.
REFERÊNCIAS
BOTAS, D.; MOREIRA, D. A utilização dos materiais didáticos nas aulas de Matemática – Um estudo no 1º Ciclo. Revista Portuguesa de Educação, 2013, 26(1), pp. 253-286.
DIENES, Z. P.; GOLDING, E.W. A geometria pelas transformações II. São Paulo: EPU, 1975. 91 p.
DIENES, Z. P.; GOLDING, E.W. Exploração do espaço e prática da medição. São Paulo: EPU, 1977. 95 p.
FIORENTINI, D.; LORENZATO, S. Investigação em Educação Matemática – percursos teóricos e metodológicos. Campinas, SP: Autores Associados, 2006. 226 p.
FISCHBEIN, E. Intuition in science and mathematics: an educational approach. London: Mathematics Education Library, 1987.
MOREIRA, M.A. Metodologias de pesquisa em ensino. São Paulo: Editora Livraria da Física, 2011. 242 p.
OLIVEIRA, M. T.; LEIVAS, J.C.P. Visualização e Representação Geométrica com suporte na Teoria de Van Hiele. Ciência e Natura. v.39 n.1, 2017, p. 108 – 117.
PAIS, L. C. Didática da Matemática. Uma análise da influência francesa. Belo Horizonte: Autêntica, 2001. 128 p.
PIAGET, Jean; INHELDER, Bärbel. A representação do espaço na criança. Porto Alegre: Artes Médicas, 1993. 507 p.
POLLARD, M. Maria Montessori. Série: Personagens que mudaram o mundo. Os
SABBATIELLO, E. E. El geoplano – un recurso didáctico para la enseñanza dinámica de la geometría plana elemental – su aplicación e utilización en la escuela primaria. Buenos Aires: Ediciones G.A.D.Y.P., 1967. 238 p.
Notas
Ligação alternative
https://periodicoscientificos.ufmt.br/ojs/index.php/reamec/article/view/5715 (pdf)

