



Artigos
COMO MEDIR INFORMAÇÃO?
HOW TO MEASURE INFORMATION?
REAMEC – Rede Amazônica de Educação em Ciências e Matemática
Universidade Federal de Mato Grosso, Brasil
ISSN-e: 2318-6674
Periodicidade: Frecuencia continua
vol. 5, núm. 2, 2017
Recepção: 19 Julho 2017
Aprovação: 04 Outubro 2017

Resumo: Por meio de ilustrações e resoluções de problemas, objetiva explicar como se mede informação. Para tal, recorre à teoria matemática da comunicação de Shannon. Esta teoria foi inicialmente elaborada para explicar transmissões de informações através de sistemas de telecomunicações a fim de corrigir erros entre a origem e o destino da informação. Mostra que a quantificação de informação parte da elaboração de estratégias de escolha entre duas mensagens ou signos. Medir informação significa contar o número de escolhas entre dois signos. Quantificar informação parte de axiomas, equações, conceitos de probabilidade e de funções logarítmicas para reduzir a incerteza do sinal de qualquer canal (meio físico) de comunicação.
Palavras-chave: Medida de Informação, Teoria da Informação, Probabilidade, Matemática, Ensino Médio.
Abstract: Through illustrations and solving equations, this project objective is to explain how to measure information. To this end, it uses the mathematical theory of communication by Shannon. This theory was originally developed to explain the transmission of information via telecommunications systems to correct errors between the source and destination information. It shows that amount of information to draw up strategies from two messages or signs. It measure information by counting the number of choices between two signs. Quantifying information is part of axioms, equations, probability concepts and logarithmic functions as a way to reduce the uncertainty of any channel signal (physical environment) communication.
Keywords: Information Measurement, Theory of Information, Probability, High School.
1. INTRODUÇÃO
Vivemos na “Era Digital”: dimensão global caracterizada pelas múltiplas conexões imbricadas entre artefatos tecnológicos digitais e seres humanos; proliferação de informação à velocidade da luz em redes de computadores; momento histórico humano Pós-Revolução Industrial caracterizado por mudanças de paradigmas sociais, econômicas, culturais, entre outras, organizadas, geridas e utilizadas com/nas/por meio de Tecnologias da Informação e Comunicação (TIC).
“As tecnologias digitais permeiam nosso cotidiano, estando presentes de formas ora evidentes, ora sutis. [...] A Teoria da Informação, desenvolvida a partir da década de 1940, é um dos pilares assim chamada da Era Digital” (PINEDA, 2006, p. 9).
Claude Shannon objetivava, por meio de sua teoria da informação ou teoria matemática da comunicação, otimizar o custo de transmissão de sinais. Ela é introduzida a partir da definição de quantificação de informação, articulada por axiomas, equações, conceitos de probabilidade e de funções logarítmicas para reduzir a incerteza do sinal. A partir daí, Shannon definiu matematicamente o conceito de informação (EPSTEIN, 1986).
A teoria da comunicação foi inicialmente elaborada para explicar transmissões de informações através de sistemas de telecomunicações a fim de corrigir erros entre a origem e o destino da informação. Shannon estava interessado em responder aos seguintes questionamentos: que recursos são necessários para se enviar informação através de um canal[2] de comunicação? Seria possível enviar a informação de maneira segura, protegida de ruído no canal de comunicação? (EDWARDS, 1971). Citamos duas preocupações referentes a estes questionamentos: companhias telefônicas, comunicações por satélites precisam saber a quantidade de informação possível a ser transmitida; as informações precisam ser enviadas de maneira segura e íntegra.
Shannon respondeu os dois questionamentos acima citados por meio de dois teoremas: teorema da codificação em canais sem ruído (analisa os recursos físicos necessários para armazenar a informação fornecida por uma fonte) e teorema da codificação em canais ruidosos (quantifica a informação que pode ser transmitida com segurança através de um canal com ruído). Existe atualmente uma grande preocupação quanto à segurança de informações. Pesquisas são realizadas nas ciências Computação, Matemática, Engenharia, entre outras ciências na busca por construção de códigos mais eficientes contra erros, técnicas de compressão/descompressão de dados, técnicas de criptografia, entre outras instâncias. Mas enquanto ao nível de ensino escolar, as unidades de medida da informação ou unidades de memória de computadores ou ainda, unidades de medida da Informática constituiriam um objeto de saber fundamental para ser ensinado e aprendido?
Segundo Mendes (2016), as unidades de memória da Informática – byte, quilobyte, megabyte, gigabyte, etc. – é um conteúdo que se configura como saber a ensinar e saber ensinado. Ou seja, esse objeto de saber é estudado em livros didáticos de matemática dos anos finais do Ensino Fundamental avaliados pelo Programa Nacional do Livro Didático (PNLD 2014), constituindo desta maneira em um objeto de saber ensinado, e também são sugeridos como objeto de saber a ser ensinado, através de diretrizes curriculares nacionais e estadual de Pernambuco. No entanto, nessa transição, Mendes (2016) verifica que a interpretação conceitual ou notação de unidades de memória da Informática é equivocada:
Em todos os livros didáticos de matemática observados, existe uma confusão em definir os prefixos e os nomes das unidades de medida da informática: ora definem o número representado por potências de base 2, ora definem a base numérica por meio de potências de base 10 para medir informação (grandeza); ambas as bases 2 e 10 preservam os mesmos prefixos do sistema métrico decimal do SI: quilo, mega, giga, etc (MENDES, 2016, p.170).
O ato de medir algo mantém, em sua essência, uma preocupação com o cunho social; abarca sentimentos e respeitos em sua ação. Na história da humanidade foram criados vários e diversificados sistemas de medições que devido a essa variedade de padrões, ocasionou um caos completo, além do mais, foram determinantes de justiça social (SILVA, 2004).
Medir significa, essencialmente, comparar. Este procedimento permite representar grandezas (comprimento, área, capacidade, etc.) através de números. Duas medidas x e y devem ter a mesma grandeza e possuir uma unidade de medida em comum. Na comparação entre x e y, poderá contar quantos “x cabe em y”. O número de vezes que “x cabe em y” é a medida. Em determinadas situações, “x não cabe em y”. Este procedimento exigirá subdividir uma das grandezas para que esta “nova” unidade de medida possa “caber” em y.
Objetivamos ensinar uma técnica de medição de informação à nível de ensino médio. Este trabalho é relevante porque:
- O objeto de estudo, medida de informação, é atual. Vivemos na “Era Digital”: momento socioeconômico e histórico atual;
- As unidades de medida de informação constituem um tema básico de aprendizagem e de ensino a nível escolar, tanto são recomendados por diretrizes curriculares nacionais, assim como são estudados em livros didáticos de matemática (MENDES, 2016);
- Por meio do ensino de medida de informação, poderá desmistificar o emprego da base 10 numérica ao invés da base 2 no seu tratamento conforme recomendações do SI (2012) e do CEI (2005);
- Contextualiza e aplica temas e domínios da disciplina matemática: função logarítmica, equações e estatística e probabilidade;
- Mantém relação com outras ciências ou disciplinas do ensino médio. O que pode auxiliar a aprendizagem de seus temas e assuntos, assim como pode dar sentido e significado aos seus estudos.
2. ELEMENTOS BÁSICOS DE TEORIA DA INFORMAÇÃO DE SHANNON
A informação parte do entendimento da existência de três elementos inseparáveis: emissor, mensagem e receptor. Quando uma pessoa envia uma informação para outras pessoas, provavelmente existirá interpretação da informação para algumas pessoas e para outras existirá ruídos[3]. Uma tomada de decisão a se pensar é enviar uma informação que gere menor interferência (ruído) possível.
O que seria melhor, informar inúmeros valores de uma tabela a outra pessoa ou apresentá-la apenas a fórmula que obtém todos os valores da tabela? Pode acontecer que o receptor não saiba ou compreenda como utilizar a fórmula para tal. Este é um código que mantém regras necessariamente compreendidas por ambos (emissor e receptor) para que exista compreensão de informação. A partir disso, informação e comunicação são dois conceitos distintos: o primeiro “depende apenas da variedade ou do número de mensagens[4] possíveis abrangidas pelo código” (EPSTEIN, 1986, p.16). Já a comunicação: “envolve o significado ou a interpretação das mensagens, que dependerá da dimensão semântica do código ao qual está referido. As mensagens só adquirem sentido quando rebatidas a códigos, e a atualização deste dá-se através das mensagens” (ibidem). Assim, o conhecimento do código deve, portanto, preceder ou no máximo ser simultâneo à troca de mensagens. Que parte da condição de que um código destinado à comunicação deve ser constituído basicamente por sinais individuais distintos entre si. Os sinais são contáveis, mas por combinação permite aumentar o número de mensagens. Na escrita, os sinais são letras e a sua combinação por determinadas regras formam palavras, frases, etc.
Informação não deve ser confundida com significado. As mensagens possuem significados, mas esses aspectos semânticos da comunicação são irrelevantes para a engenharia (de telecomunicação) (SHANNON; WEAVER, 1964). Um aspecto importante a considerar da teoria matemática da comunicação de Shannon é que a mensagem ou o signo é escolhido em um conjunto finito de elementos. O sistema de comunicação deve ser concebido tanto para operar a seleção do signo pretendido como também o não pretendido. Além disso, a medida de informação não é o número de símbolos transmitidos por segundo em um canal, mas sim a quantidade de informação transmitida por segundo, usando bits (binary digits) por segundo como sua unidade (SHANNON, 1948).
Baseado na teoria matemática da comunicação de Shannon, informação é interpretada, calculada por elementos probabilísticos. A partir dessa concepção, uma unidade de informação não é uma mensagem, percepção de ocorrências ou de um estado de coisas, mas sim a escolha entre duas mensagens ou signos. Exemplo: podemos representar uma lâmpada apagada (primeira mensagem) por “0” e acessa (segunda mensagem) por “1”. Essa lâmpada, apagada/acessa, pode funcionar como sinais alternativos, respectivamente por não/sim ou 0/1. Por outro lado, se existisse apenas uma mensagem (lâmpada acessa, por exemplo) não existiria informação, na medida que não existiria incerteza.
A própria noção de valor é muito fluente e antropomórfica para ser diretamente utilizável. Ela foi sido o ofuscamento da técnica de medição de informação até ser distinguido de significação. Tal que valor é a propriedade utilizável e aceito por um consenso comum. Ora, se partimos do entendimento de que uma mensagem é o que serve para modificar o comportamento do receptor então o valor de uma mensagem será tanto maior quanto maior ela modificar o comportamento do receptor, não necessariamente a mensagem precisa ser mais longa, mas sim mais nova. Assim, o valor da medida da informação está ligado ao inesperado, ao imprevisível, ao original. Por essa consideração, a medida da quantidade de informação se reduz à medida de imprevisibilidade, isto é, a uma teoria das probabilidades. Dessa maneira, o que é pouco provável é imprevisível e o que é certo é previsível, quanto mais imprevisível maior será a quantidade de informação (MOLES, 1978).
A essência da teoria matemática da comunicação de Shannon é: reproduzir um sinal de maneira íntegra ou com grau de fidelidade desejável; criar estratégias que possibilite a melhor maneira de escolher duas mensagens. A unidade de informação é a escolha entre duas mensagens ou signos. “O ‘bit’ é a unidade de informação ao representar a situação de escolha simples entre duas mensagens” (FIDALGO, 2004, p.3). O procedimento de escolha simples entre duas mensagens acarreta uma progressão geométrica de razão igual a 2 porque dobra a quantidade de mensagens (elementos do conjunto finito) a cada nova escolha. Vamos ver no próximo tópico que a medida de informação é essencialmente logarítmica e probabilística.
Medir informação significa, essencialmente, escolher. Este procedimento permite criar estratégias de seleção de mensagens ou signos, baseadas em elaborações de questionamentos que podem conduzir apenas respostas dicotômicas (sim ou não). Essa liberdade de escolha, em selecionar um signo ou mensagem configura-se como uma unidade de medida de informação (SHANNON, WAEVER, 1964). Se levar em consideração apenas respostas dicotômicas, então a unidade de medida de informação empregada será o bit. A partir do número de escolhas realizadas em um conjunto finito de signos ou mensagens, a quantidade de informação é definida como o logaritmo do número de escolhas, caso os signos possuam a mesma probabilidade de ocorrência. E se os signos não tiverem a mesma probabilidade de ocorrência? O que fazer? Explicaremos no próximo tópico.
A teoria da informação parte dos conceitos básicos de quantidade de informação, redundância[5] e ruído (EPSTEIN, 1986). Limitaremos esta pesquisa objetivando explicar, de maneira introdutória, como se quantifica uma informação.
O conceito de ruído é equivalente ao de erro em tecnologia da informação. No entanto, parte do pressuposto de que pode ser erro pra alguém e informação para outro. Assim, “informação equivale à redução de incertezas, oferecida quando se obtém respostas a alguma pergunta” (EPSTEIN, 1986, p.35).
A teoria da informação de Shannon apresenta princípios vinculados tanto à aplicação de canais discretos como também à canais contínuos. Esses primeiros “operam com um conjunto finito de símbolos, que mantêm correspondência biunívoca com um conjunto arbitrário de representação. O telégrafo, o teletipo, o telex e todas as formas de transmissão digital são exemplos de canais discretos” (PINEDA, 2006, p.73). Os canais contínuos são sistemas de comunicação que operam com qualquer valor ou intensidade dentro de uma faixa de valores ou intensidades determinadas. “A ausência de um repertório finito de símbolos, implica que existem infinitos valores possíveis dentro dos limites pré-determinados; esta é a característica principal das transmissões analógicas” (PINEDA, 2006, p,74). A representação de uma música num disco de vinil é um exemplo de canal contínuo. Outra diferença é que os sistemas digitais trabalham com valores inteiros enquanto que os sistemas analógicos trabalham com valores reais. Este trabalho limita-se a abordar princípios dessa teoria a canais discretos.
Segundo Edwards (1971) o objetivo da teoria da informação é medir a informação. Esta pode ser “caminhada de um ponto para outro, pode ser traduzida e pode ser armazenada. Sendo elemento essencial de qualquer sistema de controle” (ibidem, p.14).
Mostramos no tópico seguinte que é possível quantificar informação, levando-se em consideração alguns critérios. A partir de exemplos, realizamos: um processo de construção de fórmulas para quantificar informação; medições de informação.
3. METODOLOGIA
Esta pesquisa é explicativa; baseada nos procedimentos de coleta de dados, configura-se como uma pesquisa bibliográfica. Ou seja, ela é explicativa porque tem “como preocupação central identificar os fatores que determinam ou que contribuem para a ocorrência de fenômenos. Esse tipo de pesquisa que mais aprofunda o conhecimento da realidade, porque explica a razão, o porquê das coisas” (GIL, 2002, p.42).
Propomos o ensino de medida de informação à nível de ensino médio. Para tal, pesquisamos técnicas de medições de informação em artigos científicos, livros didáticos do ensino superior. Selecionamos apenas as que se aplicam aos canais discretos porque nessas técnicas são trabalhados temas e domínios da matemática do ensino médio: equações, conceitos de probabilidade e estatística, função logarítmica, entre outros; buscamos transformar didaticamente o objeto de saber – medida de informação – dito saber científico, para ser hábito ao ensino e por sua vez ensinado (saber escolar).
Este trabalho baseia-se no questionamento: “como medir informação?” mostramos elementos introdutórios, teóricos de informação e comunicação; realizamos um processo de construção de fórmulas para quantificar a informação, a partir de exemplos; ilustramos medições de informação e exemplificamos problemas que solicitam o cálculo de quantidade de informação.
4. MEDIÇÃO DE INFORMAÇÃO
Por meio do advento de computadores eletrônicos a partir do século XX, o humano sentiu a necessidade em medir a capacidade de armazenamento de dados de memória de disquetes, celulares, máquinas fotográficas digitais, CDs, etc. Enfim, necessitaram medir a quantidade de informação contida em seus artefatos tecnológicos digitais. Em decorrência dessa aplicação social atual, que tal aprendermos como se mede uma informação? Partimos por meio de um exemplo:
Considere um conjunto de 8 letras do alfabeto da língua portuguesa: A, B, C, D, E, F, G, H. Escolha uma letra e peça para um amigo seu adivinhar qual foi a letra escolhida. Seu amigo, que é muito esperto, não escolherá nenhuma das duas técnicas abaixo mencionadas:
1. Escolherá a letra aleatoriamente (“chutando”);
2. Perguntará em ordem, crescente a partir de A ou decrescente a partir de H e caso não seja ela perguntará de maneira sequencial, respectivamente, em ordem crescente ou em ordem decrescente.
Tanto a técnica 1 como a 2 utilizam-se no máximo 4 perguntas para adivinhar a letra. Mas seu amigo sabe que existe uma maneira melhor para adivinhar a letra: ele escolherá a letra do meio (a letra D ou a letra E neste exemplo). Seu amigo perguntará se a letra escolhida é anterior a letra E. Caso seja sim, continuará a perguntar se a letra escolhida está antes de C. Caso seja sim, continuará a perguntar: se a letra escolhida está anterior a letra B. Digamos que seja não. E dessa resposta adivinhará a letra escolhida (letra C). Essa técnica utiliza um total de 3 perguntas para adivinhar a letra escolhida pelo seu amigo. Assim, dizemos que as duas primeiras técnicas possuem 4 unidades de informação e a técnica escolhida pelo seu amigo possui 3 unidades de informação. Ou seja, as perguntas estabelecem uma “média de dificuldade”. Observe que aplicando a extensão do conjunto, só se faz mais uma pergunta. Configurando-se a melhor estratégia possível. Diz-se, portanto, que a quantidade de informação associada ao conjunto é de quatro unidades por letra. “Nesse sentido, a quantidade de informação é chamada “incerteza” e é indicada pela letra H. Após esta letra H, refere-se, entre parênteses, o conjunto a que se faz menção” (EDWARDS, 1971, p.47).
No exemplo anterior temos a partir da notação de incerteza de Edwards:
H(A a H) = 3 unidades por letra e H(A a P) = 4 unidades por letra. “Para distinguir entre a informação de uma afirmação e a Incerteza de um conjunto, indicaremos a primeira a letra I” (EDWARDS, 1971, p.47). Assim, a quantidade de informação contida em qualquer das soluções do exemplo anterior será I(A a H) = 3 unidades e I(A a P) = 4 unidades.
Vale destacar que I e H possuem unidades de medidas diferentes: a unidade de informação é chamada de bit e equivale à quantidade de informação associada à seleção de um entre dois eventos equiprováveis e : . A incerteza, H, é medida em bits/letra (bits por letra).
Edwards (1971) chama H de “incerteza”, enquanto que Claude Shannon chama H de “entropia”. Shannon deduziu para H uma formula que a definiu de entropia baseado em determinadas formulações de mecânica estática. Shannon estava preocupado em tratar a teoria estatística da informação, com as quantidades médias de incerteza contidas em dado conjunto (EDWARDS, 1971).
Continuando o raciocínio do exemplo acima, fazendo uma relação entre a duplicação da grandeza do sistema com o aumento do número de perguntas necessárias, resumimos estes valores no Quadro 1:
| Quantidade de elementos do conjunto (n) | Números de perguntas (H) |
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |
| 16 | 4 |
Relação entre quantidade de elementos de um conjunto e o número de perguntas
Fonte: PesquisaPor meio do Quadro 1 temos (1)
Se quisermos saber a quantidade de um conjunto, basta recorremos valores na progressão geométrica 1, 2, 4, 8, 16... para n. Caso n seja ímpar, a resposta será a mesma. Serão necessários perguntas a serem feitas.
Vale destacar que o propósito de definir a informação de maneira quantificável é possível. Portanto, é a incerteza ou a entropia própria do conjunto (incerteza máxima), definido em unidades de informação por letra do conjunto (bits/letra) e é a medida da quantidade de informação, em bits, contida em uma solução específica qualquer.
Vale destacar também que até o momento neste trabalho, estamos desenvolvendo estratégias de quantificação de informação que consideram todas as letras em termos iguais. Outro ponto a frisar é que estamos considerando I e H por técnica empregada de estratégia ótima, levando-se em consideração que apenas terá como resposta sim ou não e a sequência em ordem alfabética.
Como estamos buscando “construir fórmulas” (teoria) para quantificar informação, então precisamos generalizar a ideia anterior. Para tal, citamos mais um exemplo para adentrar nessa generalização e assim, apresentar conceitos estatísticos da teoria da informação e comunicação de Shannon.
Considere agora que seu amigo irá adivinhar uma letra de um texto de jornal escrito na língua portuguesa. É percebido que nem todas as letras aparecem no texto ou que não estariam apresentadas na mesma proporção. Daí, poderíamos ter no texto maior número de letras A do que de letras R, por exemplo, em uma proporção de duas letras para uma e mais letras T do que a letra R em uma proporção de 3:2 (três por dois) e esse texto teria pouquíssimas letras Z e Y, assim por diante. Cabe-nos agora considerar este exemplo por um tratamento estatístico. Já que, as letras apresentam proporções distintas no texto, para tal, precisamos reformular a técnica anterior apresentada no primeiro exemplo: primeiro conte a quantidade de cada letra existente no texto, em seguida calcule as suas proporções. Em seguida, coloque as letras em ordem de acordo com o seu número de proporcionalidade. Depois trace uma linha imaginária de tal maneira que o lado direito e esquerdo estejam “equilibrado”. Por fim, pergunte: a letra tal está do lado direito/esquerdo da letra tal? Com isto, reduziremos o problema em 50%. Devemos tomar como resposta sim ou não.
Suponhamos que tenha em um texto 400 letras A, 200 letras B, 100 letras C e 100 letras D. Este conjunto de letras de A à D teria a seguinte proporção: 4:2:1:1. Ou seja, quatro letras A para duas letras B para uma letra C para uma letra D. As probabilidades das letras A, B, C e D seriam respectivamente e Não vamos por estas quantidades em ordem. Mas ao invés disso, vamos preparar uma lista contendo em cada letra a relação de proporcionalidade. Assim, a lista com as letras de A à D será organizada da seguinte maneira: AAAABBCD. E a partir daí, usamos a mesma técnica apresentada no primeiro exemplo. Esta organização de letras em uma lista para um tratamento de proporcionalidade é garantida pelos seguintes cálculos: se ordenássemos as 400 letras A, 200 letras B e 100 letras C e 100 letras D teríamos uma probabilidade de escolha entre (0,5 + 0,25) e (0,125 + 0,125) caso escolhesse a letra C. O que não garantirá equilíbrio . Ou seja, para retomarmos a mesma técnica do primeiro exemplo teremos que criar uma “linha pontilhada imaginária no meio das letras”. E nessa arrumação, a lista não estaria equilibrada:

Por outro lado, se organizarmos a lista considerando a cada letra proporcionalmente à sua probabilidade, terá equilíbrio. Por tanto, poderemos traçar uma linha imaginária no “meio”, mantendo-se o equilíbrio:
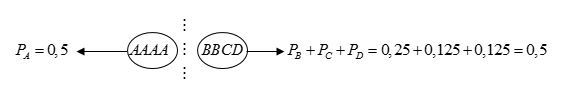
Depois dessa ordenação em uma lista, retomamos o esquema do exemplo anterior: a letra está à esquerda de B? Temos como resposta sim ou não. Na pior das hipóteses fazemos 3 perguntas no total. “A vantagem de refinar o equilíbrio de probabilidade é apenas aparente, quando nos damos conta de que nosso interesse é o de manter tão reduzido quanto possível o número médio de perguntas” (EDWARDS, 1971, p.53).
Para investigar o número médio de perguntas, iremos a seguir, calcular a média ponderada dessas quantidades de letras. Recorremos o Quadro 2 com as suas respectivas associações entre a letra escolhida (solução), o número de perguntas elaboradas para se chegar a solução e o fator de ponderação:
| Solução | Número de perguntas | Fator de ponderação | |
| A | 1 | Na 1ª pergunta feita pelo seu amigo, ele terá 50% de chance de adivinhar a letra: letra A ou letras B,C,D (4 letras de 8). | |
| B | 2 | Na 2ª pergunta feita pelo seu amigo, ele terá 25% de chance de adivinhar a letra: letra B ou letras C,D (2 letras de 8). | |
| C | 3 | Na 3ª pergunta feita pelo seu amigo, ele terá 12,5% de chance de adivinhar a letra: letra C ou letra D (1 letra de 8). | |
| D | 3 |
A média ponderada dessas quantidades é
Levando-se em conta aqueles dois exemplos, revemos a fórmula 1 para generalizá-la (Vide fórmula 2).
Pretendemos fixar um número de perguntas a fim de adivinhar uma letra entre outras diferentes e daí calcular a sua média ponderada. Destacando que só é válida quando as soluções possíveis são equiprováveis[6]. Analisando aquele último exemplo, é percebida a dependência entre os números de perguntas levantadas a fim de adivinhar a letra e o fator de ponderação. Assim, “o número de perguntas é igual ao logaritmo do fator de ponderação multiplicado por menos um” (EDWARDS, 1971, p.54). E cada fator de ponderação é igual à probabilidade do resultado correspondente. Representando o número de perguntas por , onde é o fator de ponderação. A incerteza (real) será igual a soma do produto do número de perguntas pela sua probabilidade (fator de ponderação):
(2)
A fórmula 2 é um dos teoremas elaborados por Shannon em sua teoria matemática da comunicação. No caso da fórmula 2, temos que o número de perguntas é onde I é definido como sendo a quantidade de informação que se contém em uma solução particular e K é uma constante positiva. A constante K simplesmente equivale a uma escolha de uma unidade de medida. Como estamos trabalhando com o bit, então K = 1.
Fazendo-a igual a unidade e tomando logaritmos de base dois, determinamos a grandeza da unidade de incerteza e alcançamos uma medida correspondente à anteriormente derivada de consideração em torno da sucessiva redução das probabilidades à metade (EDWARDS, 1971, p.60).
Shannon (1948) destaca que basta que saibamos as probabilidades de ocorrência de um conjunto de possíveis eventos para que encontremos uma medida de quantidade de escolhas ou de como incerto somos do resultado.
A fórmula 2 também pode ser interpretada como sendo uma equação propícia para encontrar a média da auto informação de cada símbolo do conjunto considerado ponderado por sua frequência conforme a língua (portuguesa, espanhola, etc.) considerada (EPSTEIN, 1986).
Observe que a base trabalhada no cálculo de incerteza ou de quantidade de informação ou de entropia é a base 2. Segundo Shannon (1948, p. 1) [7] a escolha da base do logaritmo corresponde a escolha da unidade de medida de informação. Se a base 2 é usada, o resultado da unidade pode ser chamado de dígito binário ou pode ser chamado por sua abreviação “bit”. “O número de escolhas sucessivas – que denominamos “unidade de informação seletiva” – é igual ao número de dígitos binários” (Edwards, 1971, p.56). Veremos a seguir o seu porquê, retomando o exemplo 1.
A técnica adotada para o seu amigo adivinhar uma letra de A à H partiu da elaboração de perguntas que tinham como resposta apenas duas possibilidades: sim ou não. Esse conjunto foi sucessivamente dividido em metades. A partir daí, a depender da letra que estaria sendo adivinhada, foi criado uma sequência de sim/não em um total de 3 perguntas em oito possibilidades diferentes (8 letras – de A à H). Por exemplo, a letra A poderia ser codificado como Sim, Sim, Sim (A letra está à esquerda de E? Sim. A letra está à esquerda de C? Sim. A letra está à esquerda de B? Sim. Então a letra adivinhada é A). Correspondendo o “Sim” à 1 e o “Não” à 0, formamos códigos binários para as 8 letras (permutação de 3x2). Assim, “o sistema de codificação S-N é, claro está, variação do sistema binário” (Edwards, 1971, p.56). No Quadro 3, expusemos as respectivas sequências de sim e não e de 1 e 0 para cada letra de A à H:
| Letras | A | B | C | D | E | F | G | H |
| Respostas | SSS | SSN | SNS | SNN | NSS | NSN | NNS | NNN |
| Códigos Binários | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
Como exemplo de aplicação, codificando letras do alfabeto (e demais caracteres, como o espaço), poderíamos enviar uma mensagem por telégrafo. Definindo o 1 ou S como sendo um bipi e o 0 ou N como sendo um bipi logo, poderíamos escrever qualquer palavra.
Vale frisar que a quantidade de informação de uma mensagem é definida na teoria da informação e comunicação de Shannon como sendo o menor número de bits necessários para conter todos os valores desta mensagem.
A partir dessas explicações sobre a fixação de uma medida de informação ou de incerteza com base em questionamentos para se chegar a uma letra adivinhada em um conjunto finito de elementos (letras), iremos, a seguir, exemplificar problemas que solicita o cálculo de quantidade de informação:
Problema1: Que quantidade de informação se contém na afirmação: “Vou completar 36 anos neste mês”? Vale frisar que o contexto é indispensável para se calcular a quantidade de informação. Suponha que hoje seja o último dia do mês. Então este conjunto considerado tem apenas um único elemento. A quantidade de informação será igual a zero bit porque bit. O enunciado não contém nenhuma informação. Agora se estivermos no dia 10 e o mês do aniversário tiver 30 dias, então este conjunto considerado tem 21 elementos. E, além disso, os 21 dias ou os 21 elementos deste conjunto são equiprováveis. Daí bits. Se o aniversariante estiver no primeiro dia do mês do seu aniversário então a quantidade de informação seria bits. Ou seja, se fôssemos adivinhar o dia do seu aniversário, precisaríamos fazer no máximo 4,9 perguntas.
Problema2: Suponha que desejamos enviar uma mensagem por meio de codificação dos meses do ano, utilizando apenas algarismos binários. Como poderíamos construir esta mensagem?
Para transferir ou armazenar os meses do ano, poderemos considerar a correspondência de números naturais (1, 2, 3, 4, ...) com os respectivos meses do ano (janeiro, fevereiro, março, abril, ...). Os números dos meses do ano podem ser convertidos para a representação em binário (código binário). Para tal, serão necessários 4 bits ( 24=16 combinações de zeros e uns). No Quadro 4 encontram-se os meses do ano codificado em notação binária:
| Meses do ano | Números naturais | Códigos binários |
| Janeiro | 1 | 0001 |
| Fevereiro | 2 | 0010 |
| Março | 3 | 0011 |
| Abril | 4 | 0100 |
| Maio | 5 | 0101 |
| Junho | 6 | 0110 |
| Julho | 7 | 0111 |
| Agosto | 8 | 1000 |
| Setembro | 9 | 1001 |
| Outubro | 10 | 1010 |
| Novembro | 11 | 1011 |
| Dezembro | 12 | 1100 |
Caso essa mesma informação fosse representada pela codificação da tabela ASCII (American Standard Code for Information Interchange), o número de bits necessários seria maior (exemplo: a letra A seria 0100.0001 e a letra M seria 0100.1101 - Utilização de 8 bits). A informação, no entanto, seria a mesma. De maneira análoga, para armazenar a informação “gênero”, podemos usar apenas um bit, representando masculino por 1 e feminino por 0. Ou, utilizamos 9 bytes para escrever as palavras: “masculino” e “feminino” (cada letra é igual a um byte ou 8 bits). A quantidade de informação “gênero” é H = 1 bit e a informação “meses do ano” possui H = 3,58 bits (ambas calculadas da fórmula 1).
Apresentamos a seguir, propriedades de entropia H, caso ela seja satisfeita:
1. É possível determinar o valor de para quaisquer valores correspondentes de probabilidade (EDWARDS, 1971);
2. Se equiprováveis todos os resultados, o valor de H aumenta com o aumento da grandeza do conjunto (EDWARDS, 1971);
3. H deve ser contínua em (SHANNON, 1948);
4. Se todos os são iguais, , então H deve ser uma função monótona crescente de n. Existirão mais possibilidades de eventos por existir probabilidades de eventos iguais (SHANNON, 1948);
5. Para um conjunto de determinada grandeza, H é máximo quando todos os resultados a esperar são igualmente possíveis (EDWARDS, 1971);
6. O valor mínimo de H é zero. Tal ocorre quando um só resultado é possível [caso ilustrado no problema 1] (EDWARDS, 1971);
7. “A unidade de informação é aditiva” [...] “A lei de adição estabelece que, se uma escolha for dividida em escolhas sucessivas, a incerteza associada ao conjunto será a soma ponderada das incertezas ligadas aos conjuntos menores” [por exemplo: ][...] “Daí decorre, por exemplo, que a unidade de informação contida em dois cartões perfurados é a soma das quantidades de informação contida em cada um deles” (SHANNON, 1948, p.10). Portanto, “se uma opção for dividida em duas escolhas sucessivas, o H original deve ser a soma ponderada dos valores individuais de H” (SHANNON, 1948, p.10 tradução nossa). Por exemplo: suponha que seu amigo irá escolher uma letra de um conjunto contendo apenas 6 elementos (as letras A, B e C). Seu amigo escolheu aleatoriamente uma letra de um conjunto contendo 6 letras. As probabilidades de adivinhar uma letra em um único evento são , respectivamente as probabilidades de escolha de um A, de um B e de um C, segundo a palavra: AABABC. Agora se fôssemos usar a técnica que utiliza perguntas sucessivas para uma lista de letras com proporções diferentes, pondo em ordem, AAABBC, teríamos as seguintes probabilidades ½ e ½ para a primeira pergunta e 1/3 e 1/6 para a segunda pergunta. Ou seja, na primeira pergunta teríamos 50% de chance para adivinhar a letra A. Já na segunda pergunta, teríamos 1/3 de chance para escolher um C e 2/3 de chance para escolher um B (Vide 8).
9. Neste caso, a quantidade de informação original é igual à soma ponderada dos valores individuais de cada quantidade de informação parcial, chamando a atenção de que 1/2, do segundo termo, é o fator de ponderação incrementado porque a segunda escolha foi reduzida à metade (50%) de chance:
Neste caso, a quantidade de informação original é igual à soma ponderada dos valores individuais de cada quantidade de informação parcial, chamando a atenção de que 1/2, do segundo termo, é o fator de ponderação incrementado porque a segunda escolha foi reduzida à metade (50%) de chance (Vide Figura 1).
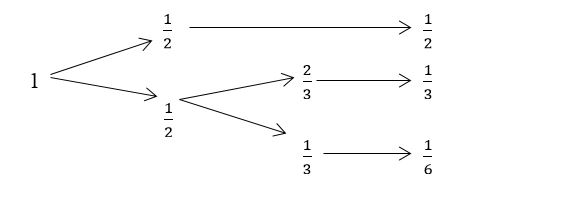
No geral temos que (3)
Onde X e Y são dois eventos, p(i, j) é a probabilidade conjunta de ocorrência onde i é para o primeiro evento e j é para o segundo evento. Portanto, a entropia de um evento conjunto é dada por:
onde e
Por essas relações temos que: p(i) é a frequência da letra ou probabilidade da letra i; pi(j) é a probabilidade de transição e p(i , j) é um digrama. Assim, a incerteza de um evento conjunto é menor que ou igual a soma das incertezas individuais dos eventos se, e somente se, os eventos são independentes, isto é P ( i, j ) = P ( i ) . P ( j ) (SHANNON,1948).
Segundo Edwards (1971), incerteza relativa é a razão entre a incerteza real e a incerteza máxima de uma fonte:

Generalizando os dois exemplos anteriores, agora vamos considerar o conjunto do alfabeto da língua portuguesa para calcular a incerteza relativa de um texto impresso. Para tal, tomemos os dados da pesquisa de Braga (2003), que selecionou aleatoriamente textos de autores brasileiros. Considerou 11 textos cada um contendo 100 KiB. Daí determinou o histograma de frequência da língua portuguesa. Tomemos os valores das frequências das letras do primeiro texto analisado por Braga (2003). O Quadro 5 contém 26 letras do alfabeto da língua portuguesa correspondendo à probabilidade pi de ocorrência de cada letra desse texto e o valor de :
| Letras | pi | -Pilog2Pï | |
| a | 0,1496 | 0,4100 | |
| b | 0,0125 | 0,0790 | |
| c | 0,0401 | 0,1861 | |
| d | 0,0497 | 0,2152 | |
| e | 0,1205 | 0,3679 | |
| f | 0,0105 | 0,0690 | |
| g | 0,0115 | 0,0741 | |
| h | 0,0138 | 0,0853 | |
| i | 0,0584 | 0,2393 | |
| j | 0,0029 | 0,0244 | |
| k | 0,0001 | 0,0013 | |
| l | 0,0305 | 0,1536 | |
| m | 0,0462 | 0,2049 | |
| n | 0,0483 | 0,2112 | |
| o | 0,1073 | 0,3455 | |
| p | 0,0251 | 0,1334 | |
| q | 0.0093 | 0,0628 | |
| r | 0,0707 | 0,2702 | |
| s | 0,0778 | 0,2866 | |
| t | 0,0442 | 0,1989 | |
| u | 0,0460 | 0,2043 | |
| v | 0,0183 | 0,1056 | |
| w | 0,0001 | 0,0013 | |
| x | 0,0025 | 0,0216 | |
| y | 0,0001 | 0,0013 | |
| z | 0,0041 | 0,0325 | |
| n | 0,0483 | 0,2112 | |
| o | 0,1073 | 0,3455 | |
| p | 0,0251 | 0,1334 | |
| q | 0.0093 | 0,0628 | |
| r | 0,0707 | 0,2702 | |
| s | 0,0778 | 0,2866 | |
| t | 0,0442 | 0,1989 | |
| u | 0,0460 | 0,2043 | |
| v | 0,0183 | 0,1056 | |
| w | 0,0001 | 0,0013 | |
| x | 0,0025 | 0,0216 | |
| y | 0,0001 | 0,0013 | |
| Letras | pi | -Pilog2Pï | (continuação) |
| z | 0,0041 | 0,0325 |
A partir dos dados do Quadro 6 temos os valores da incerteza real e da incerteza máxima que são respectivamente: 3,99 bits (da fórmula 2) e 4,7 bits (da fórmula 1). A incerteza relativa é aproximadamente 0,8489 ou 84,89% (da fórmula 4). Ou seja, caso fôssemos escolher uma letra dentre as 26 letras do alfabeto da língua portuguesa teríamos 4,7 perguntas a fazer (4,7 tentativas). A frequência com que ocorre cada letra do alfabeto da língua portuguesa presente no texto analisado por Braga (2003), é reduzida a 15,11% das tentativas de perguntas, chegando a uma média de 3,99 por letra.
Considerando que o conjunto tratado é o alfabeto da língua portuguesa, temos que ressaltar mais um ponto: a língua portuguesa possui todo um conjunto de normas, regras para serem seguidas. Por exemplo, não existem palavras na língua portuguesa com mais de três consoantes; a consoante precisa de uma vogal para formar a sílaba e ser pronunciada, mas a vogal, não. Assim, determinadas letras dependem de outras para criarem palavras, como o caso de combinações entre consoantes e vogais.
Segundo Edwards (1971), a sequência de letras que formam um trecho escrito (em português, por exemplo) é um exemplo de processo estocástico. Este é um sistema que produz uma sequência de símbolos discretos ou contínuos, segundo certas probabilidades. “Se essas probabilidades dependem de acontecimentos prévios que se restringem na série, temos o que é denominado processo de Markov[8]” (EDWARDS, 1971, p.69). Ou seja, o processo de Markov é um tipo especial de processo estocástico no qual as probabilidades dependem de eventos anteriores (SHANNON; WEAVER, 1964). Ou ainda, “uma cadeia de Markov pode ser definida como um processo probabilístico no qual o desenvolvimento futuro depende estatisticamente do estado presente e, de modo algum, pela forma com que se chegou a ele” (EPSTEIN, 1986, p.59). Portanto, “um sistema físico, ou um modelo matemático de um sistema que produz uma sequência de símbolos regidas por um conjunto de probabilidades, é conhecido como um processo estocástico” (SHANNON, 1948, p.5).
Nos processos de Markoff que podem de alguma forma gerar mensagens são classes especiais chamadas processo Ergódico, “considerando um conjunto as probabilidades de ocorrência dos eventos possíveis” (PINEDA, 2006, p.78), de forma que a quantidade de informação gerada nesse processo deverá ser a soma de todas as probabilidades pi de ocorrências de eventos, multiplicada pelo seu próprio logarítmico (ibidem). Portanto, “um ‘Processo Ergódico’ é um processo de Markov no qual não há influência apreciável interletras, para além de um número finito dessas mesmas letras [...] A linguagem comum é um exemplo de processo ergódico” (EDWARDS, 1971, p.64).
Epstein (1986, pp. 48, 49), mostra um exemplo de fonte ergódico: a frequência relativa aproximada das letras escritas a e z na língua portuguesa são respectivamente: 10,5% e 0,1%. Ou seja, a probabilidade de aparecer a letra a é 10,5% e a letra z é 0,1%. A auto informação de a e de z são respectivamente 3,25 bits e 9,96 bits (ambas calculadas da fórmula 1). Assim, a informação ou redução de incerteza trazida pela letra z é maior, em relação a que traz a letra a. Fato também comprovado na amostra de pesquisa de Braga (2003) (texto com 100 KiB) onde a probabilidade de a foi igual a 0,1496 (14,96%) e de z foi igual a 0,0041 (0,41%). E as auto informações são respectivamente 2,74 bits e 7,93 bits (ambas calculadas da fórmula 1). Ou seja, quanto mais provável for a mensagem, menor será a informação enviada; a informação dada é inversamente proporcional à sua probabilidade.
Esses resultados são comuns aparecerem no jogo chamado “Forca”. Onde é mais provável achar a palavra na língua portuguesa que comece com a letra z do que com a letra a, porque as palavras iniciadas com a letra z são menos frequentes do que as iniciadas pela letra a em um texto escrito na língua portuguesa.
Segundo Edwards (1971), para calcular a quantidade de informação contida em um processo Ergódico, é necessário conhecer a probabilidade de aparecimento do elemento seguinte (por exemplo: dependência entre as letras como as consoantes com as vogais) em qualquer estágio da sequência. A técnica adotada para realizar estes cálculos - calcular a quantidade de informação – é necessário construir uma matriz 27 x 27 (por causa das 26 letras do alfabeto da língua portuguesa mais o espaço em branco, se for considerá-lo).
Para ilustrar um cálculo partindo da consideração do processo Ergódico, adotamos mesmos dados do exemplo 1 abordado acima (não iremos considerar espaços em branco): consideramos apenas as 4 primeiras letras do alfabeto da língua portuguesa: A, B, C e D. Tendo probabilidade de ocorrência respectivamente 1/2, 1/4, 1/8 e 1/8 a partir do texto abaixo:
Assim, organizando as frequências de combinações entre duas letras em uma matriz de frequência (Quadro 6) podemos calcular a matriz de probabilidade conforme o Quadro 7:
| A | B | C | D | Total (fileira) | |
| A | 4 | 5 | 5 | 5 | 19 |
| B | 9 | 1 | 0 | 0 | 10 |
| C | 2 | 3 | 0 | 0 | 5 |
| D | 5 | 0 | 0 | 0 | 5 |
| Total (coluna) | 20 | 9 | 5 | 5 |
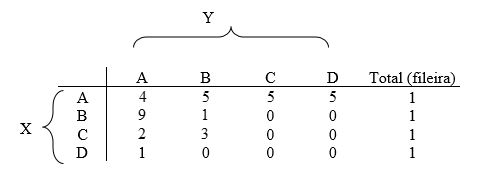
Por notação, será a probabilidade de Y em relação a X (dado X). Partindo dos valores do Quadro 7 podemos calcular, por exemplo, a quantidade média de informação de combinações de duas letras de A à D. Considere a letra A. De acordo com o texto, a próxima letra poderá ser A ou B ou C ou D. Calculando a quantidade de informação a partir da fórmula 2 temos: Ou seja,
De maneira análoga, podemos calcular as quantidades de informação que sequem B, C e D. Para calcularmos a quantidade média de informação global (de todo o texto) precisamos calcular a média ponderada. Que será a soma do produto de cada quantidade de informação de cada letra por sua respectiva probabilidade (fatores de ponderação). Esses valores estão presentes no Quadro 8.

A quantidade média de informação será a soma dos valores da última coluna:
Bits/letra
Ou seja, se considerarmos as dependências de pares de letras (digramas), a incerteza será reduzida em 0,415 bits/letra:
Bits/letra
Onde 16 é o número de digramas ou par de letras formadas por 4 x 4 letras (as 16 células da matriz); 1,75 é o resultado da fórmula 2 H(Y); A incerteza total é igual a 2 bits (resultado da fórmula 1, onde n = 4 (4 letras)); A incerteza real é igual a 1,235 bit; A incerteza relativa é igual a 38,25%.
Caso prossiga os cálculos de entropia de trigramas, determinaremos a probabilidade de surgimento de cada letra, em seguida de cada par de letras, determinando a sua entropia, denotada por Hxy(Z), por exemplo. “Recorrendo a textos cada vez mais longos, seria possível ir adiante, até que desaparecesse o valor de [entropia] H” (EDWARDS, 1971, p.68).
5. CONCLUSÃO
Para medir uma informação é necessário conhecer as probabilidades pi de cada um dos símbolos. A teoria da informação de Shannon considera informação como incerteza, tal que a informação dada é inversamente proporcional à sua probabilidade. Ou seja, quanto mais provável for a mensagem, menor será a quantidade de informação enviada. Dessa maneira, informação é uma propriedade estatística de signo ou mensagem. Informação não está relacionada sobre o que você diz, mas como o que poderia ser dito. Ou seja, podemos ter duas mensagens, uma com significados expressivos e outra com tolices. Baseado nessa teoria, ambas, as mensagens podem ter a mesma informação. Esta será o número de escolha necessária entre duas alternativas, mensagens. Verifica-se a partir dessas escolhas uma proporcionalidade, uma progressão geométrica de razão igual a 2. Tomando-se o bit como a menor unidade de medida de informação, caso consideremos todas as possibilidades com a mesma probabilidade (eventos equiprováveis), poderemos medir a informação pela fórmula: onde H é a quantidade de escolhas e n é a quantidade de elementos do conjunto. Neste caso, a entropia será máxima. Portanto, é a incerteza ou entropia própria do conjunto, definido em unidades de informação por letra do conjunto (bits/letra) e é a medida da quantidade de informação, em bit, contida em uma solução específica qualquer. Caso tomemos, um conjunto de n símbolos independentes ou n mensagens completas independentes, eventos com probabilidades de escolhas distintas p1, p2, p3, ... pi e unidades de medida de informação K qualquer, a partir disso e do cálculo da média ponderada, calculemos a entropia por onde pi são as probabilidades (fator de ponderação). Analogamente, caso tomemos um evento conjunto, calcularemos a entropia por onde
REFERÊNCIAS BIBLIOGRÁFICAS
BRAGA, Bruno da. Análise de Frequências de Línguas, 2003. Disponível em: http://www.lockabit.coppe.ufrj.br/sites/lockabit.coppe.ufrj.br/files/publicacoes/lockabit/analise_freq.pdf Acesso em: 15 jan. 2014.
CEI– Commission Electrotechnique Internationale. Norme Internacionale - 60027-2: 3ª edição, 2005.
EDWARS, Elwyn. Introdução à Teoria da Informação. Trad: Leônidas Hegenberg; Octanny Silveira. São Paulo, Editora Cultrix, 1971.
EPSTEIN, Issac (1986). Teoria da Informação. São Paulo. Editora Ática.
FIDALGO, Antônio. Informação e redundância. Os quadros da incerteza, 2004. Disponível em: http://www.bocc.ubi.pt/pag/fidalgo-antonio-quadros-incerteza.pdf Acesso em: 19 jan. 2015.
GIL, A. C. Como elaborar projetos de pesquisa. 4ª. ed. São Paulo: Atlas, 2002.
MOLES, Abraham. Teoria da informação e percepção estética. Trad: Helena Parente Cunha. Brasília, Editora Universidade de Brasília, (1978).
PINEDA, J. O. C. A entropia segundo Claude Shannon: o desenvolvimento do conceito fundamental da teoria da informação. Dissertação de mestrado em História da Ciência, São Paulo, Pontifícia Universidade Católica, 2006.
SHANNON, Claude E. A Mathematical Theory of Communication. The Bell System Technical Journal, Vol. 27, pp. 379–423(part 1), 623–656 (part 2), July, October, 1948.
SHANNON, Claude, E; WAEVER, Warren The Mathematical Theory of Communication. The University of Illinois Press. Urbana, 1964.
SI: Sistema Internacional de Unidades. Traduzido de: Le Système international d’Unités: Duque de Caxias, RJ: INMETRO/CICMA/SEPIN, 2012.
SILVA, Irineu da. História dos pesos e medidas. São Paulo, EdUFSCar, 2004.
Notas
No geral, temos: Substituindo em (2) teremos: C.Q.D
Ligação alternative
https://periodicoscientificos.ufmt.br/ojs/index.php/reamec/article/view/5377 (pdf)

