



O APPRENTI GÉOMÈTRE 2 COMO UM RECURSO TECNOLÓGICO PARA O ESTUDO DA COMPARAÇÃO DE ÁREAS DE FIGURAS PLANAS: A APROPRIAÇÃO DE LICENCIANDOS EM MATEMÁTICA
THE APPRENTI GÉOMÈTRE 2 AS A TECHNOLOGICAL RESOURCE FOR THE COMPARASION STUDY OF AREAS OF FLAT FIGURES: THE APPROPRIATION OF UNDERGRADUATES IN MATHEMATICS
REAMEC – Rede Amazônica de Educação em Ciências e Matemática
Universidade Federal de Mato Grosso, Brasil
ISSN-e: 2318-6674
Periodicidade: Frecuencia continua
vol. 7, núm. 1, 2019
Recepção: 31 Janeiro 2019
Aprovação: 21 Março 2019
Resumo: A presente pesquisa descreve como dois licenciandos em matemática se apropriaram do Apprenti Géomètre 2 para o estudo da comparação de áreas de figuras planas. Adotou-se para a devida análise a Teoria Instrumental, em especial o processo de Gênese Instrumental, proposta por Pierre Rabardel (1995). Na busca de verificar como os participantes se apropriaram do recurso tecnológico se aplicou uma atividade, contemplando duas questões, sobre a temática em estudo. Os resultados da pesquisa evidenciaram que ocorreu o processo de Gênese Instrumental. A instrumentalização foi perceptível no momento em que os licenciandos em matemática manipulavam o software e ressaltavam estratégias de resoluções para a atividade com os distintos menus e ferramentas, os associando aos seus conhecimentos matemáticos. Já a instrumentação foi designada no momento da ação, ou seja, quando os licenciandos em matemática usaram seus conhecimentos e os integraram aos elementos do software para resolver a atividade, se obtendo a resolução. O trabalho em dupla dos licenciandos em matemática para resolver a atividade, sobre comparação de áreas manipulando o Apprenti Géomètre 2, permitiu o desenvolvimento dos três esquemas de utilização (uso, ação instrumentada e atividade coletiva instrumentada).
Palavras-chave: Comparação de áreas, Apprenti Géomètre 2, Gênese Instrumental.
Abstract: The present research describes how two undergraduates in mathematics appropriated Apprenti Géomètre 2 for the study of the comparison of areas of flat figures. The Instrumental Theory was adopted for the proper analysis, especially the process of Instrumental Genesis, proposed by Pierre Rabardel (1995). In the search to verify how the participants appropriated the technological resource, an activity was applied, contemplating two questions, on the subject under study. The results of the research evidenced that the process of Instrumental Genesis occurred. The instrumentalization was perceptible at the moment when the mathematics undergraduates manipulated the software and emphasized resolution strategies for the activity with the distinct menus and tools, associating them with their mathematical knowledge. Already, the instrumentation was assigned at the moment of action, that is, when the undergraiduates in mathematics used their knowledge and integrated them to the elements of the software to solve the activity, obtaining the resolution. The double work of the undergraduates in mathematics to solve the activity, on comparison of areas manipulating the Apprenti Géomètre 2, allowed the development of the three schemes of use (use, instrumented action and instrumented collective activity).
Keywords: Comparison of areas, Apprenti Géomètre 2, Instrumental Genesis.
1. INTRODUÇÃO
Desde o surgimento das tecnologias, o campo educacional tem sido enriquecido com as ferramentas tecnológicas que contribuem como um auxílio para o processo de ensino e de aprendizagem. Usá-las no contexto educacional possibilita diversificar e tornar esse espaço mais dinâmico e reflexivo do modelo habitualmente usado da sala de aula, no qual, gira em torno do professor- aluno-Livro Didático (LD).
Ao se utilizar ferramentas tecnológicas no ambiente da sala de aula, o professor deve se apropriar desses recursos na busca de integrá-los a sua prática de ensino e usá-los com finalidades pedagógicas com o intuito de evidenciar um melhor processo de ensino. Esse exercício permite ao devido professor, profissional responsável por ensinar e disseminar a aprendizagem nos seus alunos, se tornar reflexivo com a sua própria metodologia. Então o termo integrar é diferente de inserir?
A presente pesquisa parte do pressuposto que apesar de serem palavras que podem possibilitar o mesmo entendimento, possuem significados e contextos totalmente distintos quando se pretende elucidar o trabalho com algum recurso no âmbito educacional. Enquanto à integração visa proporcionar por meio de um dado recurso um melhor processo de ensino possibilitando a aprendizagem, a inserção aborda apenas a sua aplicação em que geralmente não se vislumbra como produto educacional final a aprendizagem, e sim o atrativo para aulas.
Mediante essa distinção, essa investigação direciona o olhar para a integração das ferramentas tecnológicas analisando como dois licenciandos em matemática se apropriam do Apprenti Géomètre 2 para resolver situações sobre a comparação de áreas. A opção por esses participantes se justifica pelo fato dos mesmos estarem em formação inicial e sua interação com ferramentas tecnológicas os auxiliam a entender que é possível trabalhar um conteúdo de maneira diversificada do método tradicional (professor, aluno, LD, quadro e pincel - escrever no quadro).
Escolheu-se o Apprenti Géomètre 2 por ser um software que permite a exploração de distintos conceitos matemáticos, em especial, o trabalho com a área. Pesquisadores (SILVA, 2016; PACHÊCO, 2018) enfatizam que esse software para o estudo da área se destaca pelo fato de conceber cinco menus e em cada um deles existir diversas ferramentas que os integram, podendo-se trabalhar com uma pluralidade de tipos de resolução.
Na busca de suprir todas as informações descritas, se adotou como procedimentos metodológicos a aplicação de uma atividade sobre a situação de comparação de áreas. Para resolvê-la foi proposto que os participantes usassem o Apprenti Géomètre 2, software de Geometria, pois suas ferramentas possibilitam ao usuário usar estratégias diversas para a obtenção de resolução, sem perda de propriedades do objeto matemático.
Olhou-se para a situação de comparação de áreas de figuras planas sobre o estudo da pesquisadora Baltar (1996). Já para a abordagem da construção do conceito de área enquanto grandeza tomou-se como referências as autoras Douady e Perrin- Glorian (1989) que enfatizam a relevância de associar e distinguir os quadros geométrico, numérico e das grandezas.
Com o intuito de analisar a disposição dos licenciandos em matemática ao se apropriarem do Apprenti Géométre 2 para resolver situações de comparação de áreas, usou-se a Teoria Instrumental (TI), proposta por Pierre Rabardel (1995). Adotou-se a TI por permitir analisar como pessoas se apropriam de um artefato, na busca de resolver atividade sobre algum objeto de conhecimento, transformando progressivamente o artefato em instrumento.
A partir das informações descritas, a pesquisa busca resolver as seguintes indagações: de que maneira dois licenciandos de matemática se instrumentalizaram com as ferramentas do Apprenti Géomètre 2 no estudo da comparação da área de figuras planas? Quais conhecimentos matemáticos foram mobilizados pelos participantes no ambiente da ferramenta tecnológica para resolução do estudo da comparação da área de figuras planas? Qual (is) esquema (s) de utilização (ões), segundo a TI, é (são) evidenciado (s) no presente estudo?
Baseado com os questionamentos propostos se têm como objetivo geral: analisar a apropriação de dois licenciandos em matemática relativo ao uso do Apprenti Géomètre 2 no estudo da comparação de áreas de figuras planas à luz da Teoria Instrumental. De modo a complementá-lo se adotou os objetivos específicos: identificar quais esquemas foram mobilizados pelos licenciandos ao manipularem o Apprenti Géomètre 2 na busca de obter a comparação de áreas, e identificar os possíveis momentos da instrumentalização e instrumentação ocorridos no estudo da comparação de área.
Por fim, se elucida que o próximo tópico contempla a abordagem da fundamentação teórica, sendo seguida pelos procedimentos metodológicos, análises e discussão dos resultados, considerações finais e referências utilizadas como aporte para produção da pesquisa.
2. REFERENCIAIS TEÓRICOS
2.1. A Grandeza área: uma breve abordagem
A abordagem da área enquanto grandeza geométrica, nesta pesquisa, se apoia nos estudos elaborados por Douady e Perrin-Glorian (1989). Essas pesquisadoras, em um contexto francês, por meio de uma engenharia didática notaram vários erros cometidos por alunos ao resolverem atividades que conduziam a construção do conceito da grandeza área, entre elas:
A superfície unitária sendo uma superfície com certa forma faz com que a possibilidade de medida de uma superfície dependa de S ser efetivamente ladrilhável com elementos daquela forma. Assim, os alunos encontram dificuldade para exprimir a área de um triângulo em cm2 (centímetros quadrados), dada a impossibilidade de cobri-lo com número finito de quadrados; A área é ligada à superfície e não se dissocia de outras características dessa superfície; Se o perímetro de uma superfície se altera sua área também (e reciprocamente). Se duas superfícies têm o mesmo perímetro, elas têm a mesma área. Estende-se o uso de certas fórmulas a situações em que elas não são válidas: por exemplo, produto de duas “dimensões” para obter a área de um paralelogramo ou o produto das três “dimensões”, no caso de um triângulo (DOUADY; PERRIN-GLORIAN, 1989, p. 394).
Esses entraves, de acordo com as pesquisadoras, é fruto de um tratamento atribuído pelos alunos que a área está relacionada a forma da superfície ou apenas a medida da superfície. Diante da realidade apresentada pelos alunos, contemplou-se que eles ao se depararem com situações que envolviam o conteúdo de área mobilizaram duas concepções, sendo elas: a concepção geométrica e a concepção numérica.
A concepção geométrica caracterizada pelos alunos vincula a área ao formato da superfície. Por exemplo, dada uma dada superfície F (quadrado), se a mesma passasse pelas transformações de decomposição e recomposição, sem perda de suas propriedades, e como produto final se obtivesse um paralelogramo os alunos ressaltavam que ambas possuíam áreas distintas, pelo fato de seus formatos serem diferentes.
Já a concepção numérica se define pelo fato dos alunos associarem a área ao número. Se torna perceptível que os alunos, muitas vezes, criavam fórmulas e tentavam resolver como uma forma unilateral as atividades de área apenas pelo aspecto numérico, relegando outros procedimentos, por exemplo, inclusão, sobreposição, decomposição, recomposição e outros.
Se percebe por meio dos resultados elucidados pelos alunos que eles desenvolveram as concepções geométricas e numéricas, mas não as articulavam, ou seja, foram desenvolvidas de maneiras isoladas.
Com base nessas dificuldades apresentadas pelos alunos, Douady e Perrin-Glorian (1989) salientam que para se construir o conceito de área é necessário se interligar os quadros geométricos, numéricos e das grandezas. Elas, ainda, discutem que essa associação favorece a superação das concepções (geométricas e numéricas) e possibilita a aprendizagem da temática de maneira mais sólida, sem ser unilateral.
A partir do estudo de Douady e Perrin-Glorian, Baltar (1996) realizou um prolongamento propondo três situações (comparação, medida e produção) que dão sentido ao conceito de área, no qual se articulam aos quadros geométricos, numéricos e das grandezas. Os resultados desse estudo, também fruto de uma engenharia didática, evidenciou que alguns alunos concebiam apenas as concepções geométricas e numéricas.
Ao propor as três categorizações, Baltar (1996) elucidou que
As situações de comparação se situam essencialmente em torno do quadro das grandezas. Quando comparamos duas superfícies somos conduzidos a decidir se elas pertencem ou não a uma mesma classe de equivalência. É claro que, com frequência, os quadros geométrico e numérico vão ser necessários para a resolução dos problemas de comparação, mas sua intervenção em geral é secundária com relação à do quadro das grandezas. Nas situações de medida, destacam-se o quadro numérico e a passagem da grandeza ao número por meio da escolha de uma unidade. O resultado esperado numa situação deste tipo é um número seguido de uma unidade. As situações de produção são diferentes das anteriores do ponto de vista da tarefa cognitiva do aluno. Enquanto nas situações de comparação e medida em geral há apenas uma resposta correta para cada situação, as situações de produção, frequentemente admitem várias respostas corretas. Além disso, apesar de a resposta esperada para uma situação de produção ser uma superfície (objeto geométrico), a intervenção dos outros quadros pode ser tão importante quanto a do quadro geométrico. (BELLEMAIN; LIMA, 2002, p. 45).
A partir dessas categorias de Baltar (1996), a presente pesquisa se deteve apenas no estudo das comparações de áreas. Se entende que as demais situações são essenciais para a abordagem da construção do conceito da grandeza área, mas a opção da comparação de áreas possibilita, por meio do Apprenti Géométre 2, entender como dois licenciandos em matemática resolvem atividades que os permitam usar estratégias com ou sem aspectos numéricos.
2.2. O Apprenti Géomètre 2: uma apresentação de seus menus e ferramentas
Ao se falar em recursos no âmbito escolar é imprescindível mencionar as contribuições das tecnologias para o processo de ensino e de aprendizagem. Elas, na atualidade, estão integradas nas mais diversas situações do nosso dia a dia (Shopping, Aeroporto e etc) e o ambiente escolar não se distância dessa realidade.
Sua participação no contexto educacional, em especial na sala de aula, permite auxiliar o professor conduzir finalidades pedagógicas que o ajude no desenvolvimento de sua aula para contribuir na aprendizagem de seus alunos. Advindo dessa perspectiva, essa pesquisa se dispõe a analisar como licenciandos em matemática utilizam o Apprenti Géométre 2 para resolver situações sobre a comparação de áreas.
O Apprenti Géométre 2 é um software de geometria criado no “Centre de Recherche sur l’Enseignement des Mathématiques - (CREM) na comunidade francófona da Bélgica. Apesar de ser designado como um software de geometria, é possível trabalhar outros conceitos matemáticos, por exemplo, ponto, reta, plano, área, perímetro, frações e outros. Para uma melhor familiarização é exposto por meio da Figura 01 a tela de reprodução do software.

O Apprenti Géométre 2 contempla cinco menus (A, B, C, AB e AC), nos quais os menus AB e AC são formados pelas composições das ferramentas que integram os anteriores. Este software permite a acessibilidade do usuário como “aluno” e/ou “professor”.
Algumas distinções entre os menus são perceptíveis no que concerne ao uso do software, entre elas: as ferramentas denominadas de figuras padrão integram apenas o menu A ou seus derivados (AB e AC).
Os menus B e C não possuem as ferramentas padrões, nos quais disponibilizam a construção de figuras já pré-configuradas no próprio software, mas concebem as Figura a mão livre. Apesar de conceberem praticamente as mesmas ferramentas, elas possuem uma pequena distinção, que se trata: no menu B as ferramentas não disponibilizam a construção de retas infinitas, algo que é possível no menu C. A seguir, por meio da Figura 02, é exposto o ambiente do menu AB, de maneira ilustrativa para situar aos leitores as ferramentas que compõe os menus, como supracitado.
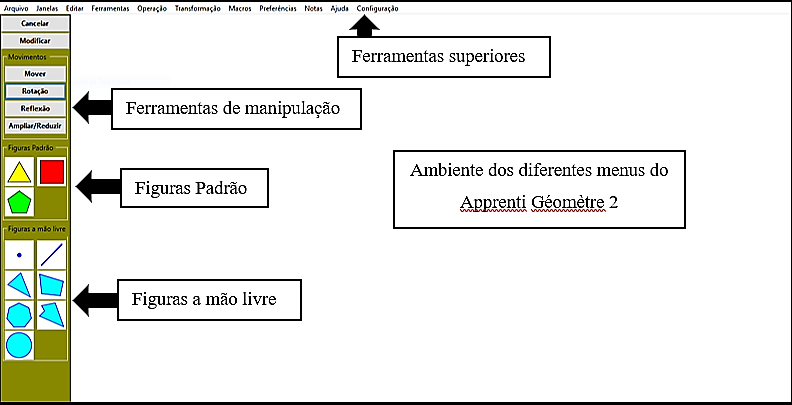
A partir da análise da Figura 02 se nota quais ferramentas compõe cada menu, como já foi descrito. Os menus AB e AC, por serem a composição das ferramentas anteriores, possuem as figuras padrão, juntamente com as figuras mãos livres e outras, pois as ferramentas desses menus são a composição dos seus anteriores (A+B) = AB; (A+C) = AC.
2.3. A transformação de artefato em instrumento discutidas na Teoria Instrumental
A TI elaborada por Rabardel (1995) se baseia na ideia de que o trabalho com ferramentas e atividades contribuem para a aprendizagem do ser humano. Oriunda de influências da ergonomia cognitiva e elementos da psicologia, permite verificar como pessoas se apropriam de ferramentas e as utilizam para realizar atividades, no qual, durante esse processo de obtenção das respostas mobilizam conhecimentos prévios ou práticos durante sua resolução.
As contribuições da ergonomia cognitiva, segundo Falzon (2007) se “[...] trata dos processos mentais, tais como a percepção, a memória, o raciocínio e as respostas motoras, com relação às interações entre as pessoas e outros componentes de um sistema”. No que se refere a psicologia, Rabardel aborda o conceito de esquema como um mecanismo de ações no qual as pessoas interagem com a ferramenta e/ou outras pessoas na busca de obter o resultado da atividade.
A partir dessa mediação de dinamismo entre pessoa agindo com a ferramenta na busca de resolver a atividade sobre um determinado objeto de conhecimento, Rabardel ressalta que é essencial a distinção entre artefato e instrumento.
Rabardel (1995) utiliza o termo artefato para denominar objetos manipuláveis ou simbólicos. Nesse sentido, ele pode ser compreendido como sendo um intermédio para a ação.
Já o instrumento é entendido como “uma totalidade que compreende ao mesmo tempo um artefato (ou fração de artefato) e um ou mais esquemas de utilização” (RABARDEL, 1995, p. 93). De modo geral, o instrumento possibilita ao sujeito o conhecimento sobre objeto em estudo, exercendo papel de mediar a ação para o objeto.
Na busca de resolver uma determinada atividade, o sujeito utiliza o artefato para sua realização (ação inicial) e para se obter a resposta desejada é necessário pensar no modo de resolvê-la (esquemas de utilizações) com o auxílio do artefato. Esse procedimento integra o artefato, transformando-o em instrumento que possibilita a ação final, ou seja, o alcance da resposta.
Os esquemas definidos por Rabardel (1995) emergem a partir do uso do artefato, no qual dependem da função que exerce na ação da realização da atividade, sendo, portanto, concernente a duas dimensões, são elas: as atividades principais que são destinadas quando o artefato é o meio para sua realização. Já as atividades do tipo secundárias o artefato possui características próprias para efetivação de sua realização.
Os esquemas de utilizações, de acordo com Rabardel (1995), podem ser destacados em: 1º- os Esquemas de Uso (EU) que correspondem as tarefas secundárias, isto é, a utilização dos elementos do artefato nos quais podem ser denominados de “pré-definidos”; 2 º- Esquemas de Ação Instrumentada (EAI), integram as ações dos EU, no qual se direcionam para as atividades do tipo principal e são destinados como sendo o meio para o objeto da atividade; 3º- Esquemas de Atividade Coletiva Instrumentada (EACI). Esse tipo de esquema corresponde a usar de maneira simultânea ou agrupada um instrumento para realização de atividade como uma forma compartilhada ou coletiva.
De modo geral, os EU e EAI podem assumir o mesmo estatuto mediante a realização de uma atividade. Já os EACI, apesar do trabalho em grupo, os sujeitos mobilizam seus esquemas de maneira individuais, no qual buscam o mesmo intuito, resolver a atividade. Apesar dessas categorizações se tem que os esquemas de utilizações são dependentes.
Ao se apropriar do artefato e realizar ações sobre ele na busca de obter respostas da atividade, o sujeito torna possível analisar os processos de instrumentalização e instrumentação que compõe o cerne da Gênese Instrumental (transformação progressiva do artefato em instrumento).
A instrumentalização é direcionada para o artefato, isto é, como o sujeito se apropria das propriedades do artefato. E a instrumentação surge quando o foco é direcionado para o sujeito, ou seja, no qual se objetiva a assimilação e integração dos distintos esquemas originados e por meio deles se obtém o resultado da atividade.
É válido mencionar que em ambos os processos há desenvolvimento de esquemas, embora com um pequeno diferencial: na instrumentalização o sujeito constrói esquemas relacionados as potencialidades e limitações do artefato. Já na instrumentação os esquemas são desenvolvidos para responder a atividade, ou seja, a parte prática do estudo.
Como uma forma de analisar esses dois processos, Rabardel dispõe do modelo de situações de atividades instrumentais – SAI, conforme ilustra a Figura 03.
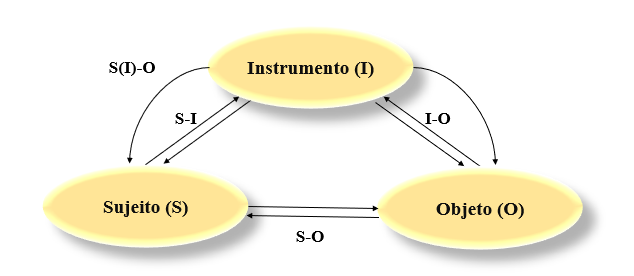
A Gênese Instrumental é um processo de muita complexidade e como uma maneira de entender essas multiplicidades das diversas relações que existem entre os polos sujeito (S), instrumento (I) e objeto (O), Rabardel a analisa por meio do modelo SAI. No qual a instrumentalização ocorre com base nas interligações entre os polos: [S(I)-O]; [I-O]; [S-O], e a instrumentação direciona seu olhar para os polos [S-I].
3. MATERIAIS E MÉTODOS
Com o intuito de analisar como dois licenciandos em matemática se apropriam do Apprenti Géomètre 2 no estudo da comparação de áreas de figuras planas, foi proposto uma atividade para sua resolução sobre a temática e por meio dela verificar, à luz da TI, as interligações que situam os três polos (Sujeito - Instrumento – Objeto) do modelo SAI, conforme expõe a Figura 04:

A atividade, sendo composta por duas questões, objetivou analisar como dois licenciandos em matemática mobilizavam seus conhecimentos matemáticos interligando às diversas ferramentas disponibilizadas no ambiente do Apprenti Géomètre 2.
A primeira questão, conforme apresenta a Figura 05, teve por intuito articular a passagem do quadro geométrico com o das grandezas, relegando o numérico. É perceptível que a passagem do quadro geométrico para o das grandezas evidencia a relação de ter a mesma área (Douady; Perrin-Glorian, 1989), no qual, segundo essas autoras, devem ser ensinadas anteriormente ao uso da medida de área.

Esse tipo de atividade, ilustrada a partir da Figura 05, conduz a se refletir a área como uma grandeza, isto é, enquanto um atributo da figura, e, não associado apenas a um número ou ao formato específico desta.
A segunda questão, como apresentada por meio da Figura 06, permite duas acessibilidades para resolução, isto é: a primeira mediante a articulação dos quadros geométricos e das grandezas, relegando o quadro numérico.
Já na segunda, a interligação entre o quadro das grandezas com o numérico. É possível realizar o ladrilhamento efetivo das figuras ao se adotar uma unidade de medida padrão, portanto, procedimento de contagem permite a obtenção da comparação da área.

Este tipo de atividade possibilita a compreensão de que a área é um atributo da figura, pois distintas superfícies podem ter a mesma área. Além disso, nota-se que neste tipo de situação, diferentemente da primeira atividade, também, é possível comparar a área por meio do ladrilhamento efetivo, ou seja, medir a figura com unidade de medida de área.
Para resolução da atividade, no qual contempla duas questões, o software foi o mediador para que os licenciandos em matemática a resolvessem. Nessa pesquisa os dois participantes se agruparam, formando uma dupla. Cabe mencionar que os participantes investigados responderam toda a atividade no notebook, ou seja, não houve impressão de nenhum documento para aplicabilidade do estudo. Para coletar os dados, usou-se o programa aTuber Catcher, em especial a função captura de tela em vídeo, na busca de verificar todo o processo resolutivo de manipulação dos licenciandos no Apprenti Géomètre 2 para obter o resultado da atividade.
O trabalho em dupla permitiu identificar os esquemas de utilizações, propostos por Rabardel (1995), que surgiram no decorrer da resolução da atividade que teve uma duração de duas horas.
Os dois licenciandos em matemática, participantes voluntários, integram o corpo discente de uma instituição de ensino superior pública do estado de Pernambuco. A escolha por apenas dois participantes se concebe ao fato de que é possível analisar com mais ênfase o processo de apropriação do Apprenti Géomètre 2, esquemas de utilizações e a transformação progressiva do artefato em instrumento (Gênese Instrumental).
O processo de Gênese Instrumental (instrumentalização e instrumentação) é complexo e por isso se optou por investigar apenas uma dupla de participantes, uma vez que, abre margens para futuras pesquisas analisar a temática com mais ênfase e maior demanda de tempo.
4. RESULTADOS E DISCUSSÃO
A presente pesquisa, subsidiada pelo Modelo SAI, descreve nesse tópico a interligação entre esses três polos: Licenciandos (S)–Instrumento (I)–Objeto (Comparação de áreas). Antes da aplicabilidade da atividade se pediu que a dupla utilizasse os seguintes procedimentos:
- 1º Vá na área de trabalho do notebook e clique no ícone do programa (Apprenti Géomètre 2). Após o software realizar sua reprodução para a tela inicial, clique na opção “aluno” e digite Licenciandos, selecione o idioma e menu com o qual deseja trabalhar, isso feito, clique em OK;
- 2º Com o menu aberto, clique em “arquivo” selecione a opção “abrir”. O Apprenti Géomètre 2 irá se direcionar a área de trabalho do notebook. Nesse sentido, selecione a pasta nomeada de “Comparação de áreas”. Em seguida, a questão que deseja resolver;
- 3º É válido mencionar que esse procedimento deve ser realizado para as duas questões, pois suas resoluções são individuais (uma por vez);
- 4º É possível a alteração do menu, caso desejem. Posteriormente aos procedimentos supracitados já é possível a manipulação do Apprenti Géomètre 2;
- 5º Quando finalizarem a resolução de cada questão devem selecionar a opção “arquivo” e em seguida “salvar” para registrar o produto (resolução final) do estudo.
Os procedimentos para reproduzir as atividades foram realizados perfeitamente e podem ser visualizados por meio da Figura 07.

Uma limitação que se percebeu no devido software é que sempre ao clicar em seu ícone as informações reproduzidas na tela de entrada, que são contempladas com as funcionalidades (idioma e menu), são as mesmas adotadas na utilização anterior, cabendo assim ao usuário alterá-las.
Ao seguirem as instruções, os participantes selecionaram a primeira questão e começaram a navegar pelas ferramentas do software (menu superior, figuras mão livre e figuras padrão) no menu AB, como ilustra a Figura 08.
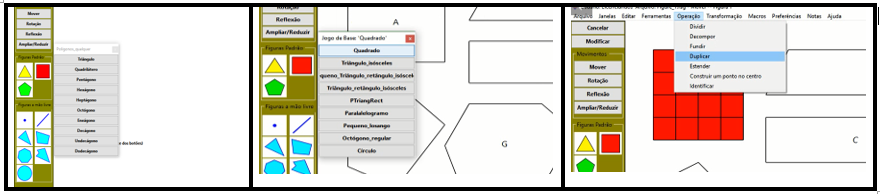
Após a manipulação de algumas ferramentas do menu AB, os licenciandos enfatizaram, a princípio, que seria possível obter a resposta sem usar a unidade de medida. Tomando como base a figura A para se comparar a área das demais figuras (B, C, D, E, F, G, H, e I), a dupla iniciou o procedimento comparativo entre as figuras A e C.
Os conhecimentos matemáticos mobilizados, nesse momento, se destinavam a decompor a figura C em duas partes e posteriormente compará-la a figura A, por meio da sobreposição. Para isso selecionou-se a opção dividir, dividir em duas partes na figura C, como apresenta a Figura 09, porém não se obteve êxito.
Pela captura de tela em vídeo, usada pelo programa aTube Catcher, é perceptível observar que os licenciandos clicam na figura C, e pensam que ela seria dividida automaticamente, mas esses procedimentos não foram realizados. De acordo com a TI, nesse momento prático, pode-se enfatizar que esses participantes estão se instrumentalizando com as devidas funcionalidades das ferramentas usadas para fazer a divisão da figura C.
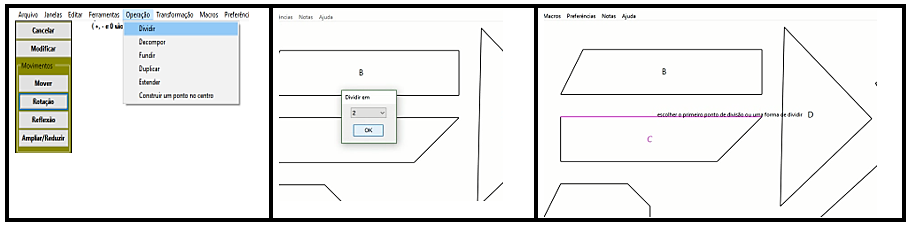
Com base nessa vivência, os participantes redirecionam suas estratégias resolutivas, ou seja, preferem utilizar a unidade de medida para resolver essa questão. Na busca de adotá-la (unidade de medida padrão) é acionado o conjunto de figuras padrão e mediante suas diversas ferramentas o quadrado de cor vermelha é a figura escolhida para a realização da técnica do ladrilhamento.
Como uma forma de alcançar o resultado de maneira mais rápida, os licenciandos selecionam a opção duplicar, disposto no AG2. Após essa seleção, duplicam os quadradinhos (unidade de medida da cor vermelha) repetidamente para ladrilhar a figura A.

Quando a figura A é ladrilhada, por meio do auxílio da unidade de medida, como se pode observar na Figura 11, os licenciandos enfatizam que sua área, nesse caso, corresponde a 16 quadrinhos.

Posteriormente a obtenção do ladrilhamento efetivo da figura A, como ilustra a Figura 11, os participantes tentam realizar a mesma técnica resolutiva na figura B, mas não conseguem ladrilhá-la por completo. Por causa disso, eles saem do menu AB por acharem que não há ferramentas suficientes para resolvê-la e selecionam o menu AC.
Ao abrirem o menu AC os licenciandos retomam a realizar a comparação das figuras, mas sem considerar os aspectos da unidade de medida. De modo a diferenciar os conhecimentos mobilizados por eles no início da resolução, a técnica adotada como se pode observar na Figura 12 se trata da decomposição, recomposição e sobreposição de figuras planas.
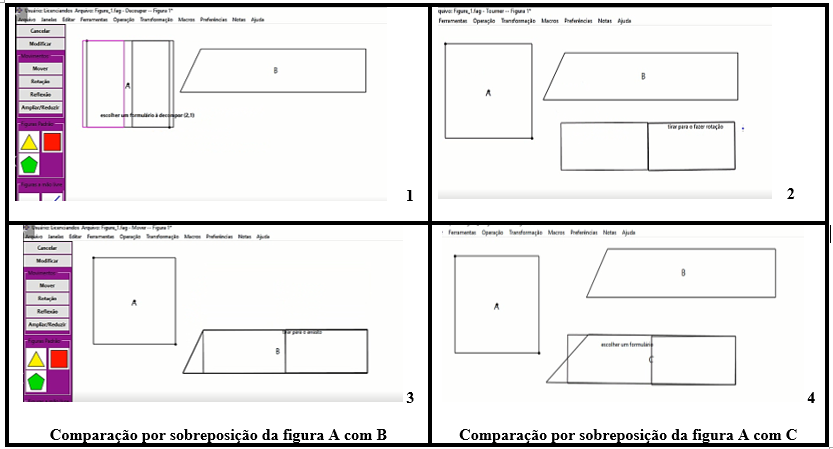
Ao se adotar procedimentos geométricos observa-se que as duas partes decompostas da figura A quando são recompostas formam uma retângulo, como é possível ver na Figura 12 (quadradinho número 2). Por meio desse retângulo, se nota que os conhecimentos mobilizados pela dupla são geométricos contemplando aspectos do quadro das grandezas, ou seja, ter ou não a mesma área (relação de equivalência).
Nota-se que as figuras B e C são comparadas por meio da sobreposição das partes que compõe a figura A. A partir disso tem-se que a figura B tem área maior que a figura A. Já a figura C tem área igual a figura A.
As estratégias utilizadas para a comparação das figuras (E, F, G e I) com a figura A são de inclusão e sobreposição, no qual podem ser visualizadas na Figura 13.

Na comparação das figuras D e H com a figura A percebe-se que elas sofrem as transformações de decomposição e recomposição, conforme ilustra a Figura 14. A figura D (triângulo) é decomposta e recomposta em formato de quadrado. Já a figura H também é decomposta e recomposta, mas, além disso, a superfície é colorida.

Após todos os procedimentos descritos, os licenciandos concluíram a primeira questão. Como uma maneira de sintetizar suas respostas, propuseram que: as figuras da cor verde possuem a mesma área que A, as figuras da cor vermelha possuem área maior que A e as figuras da cor cinza possuem área menor que A.
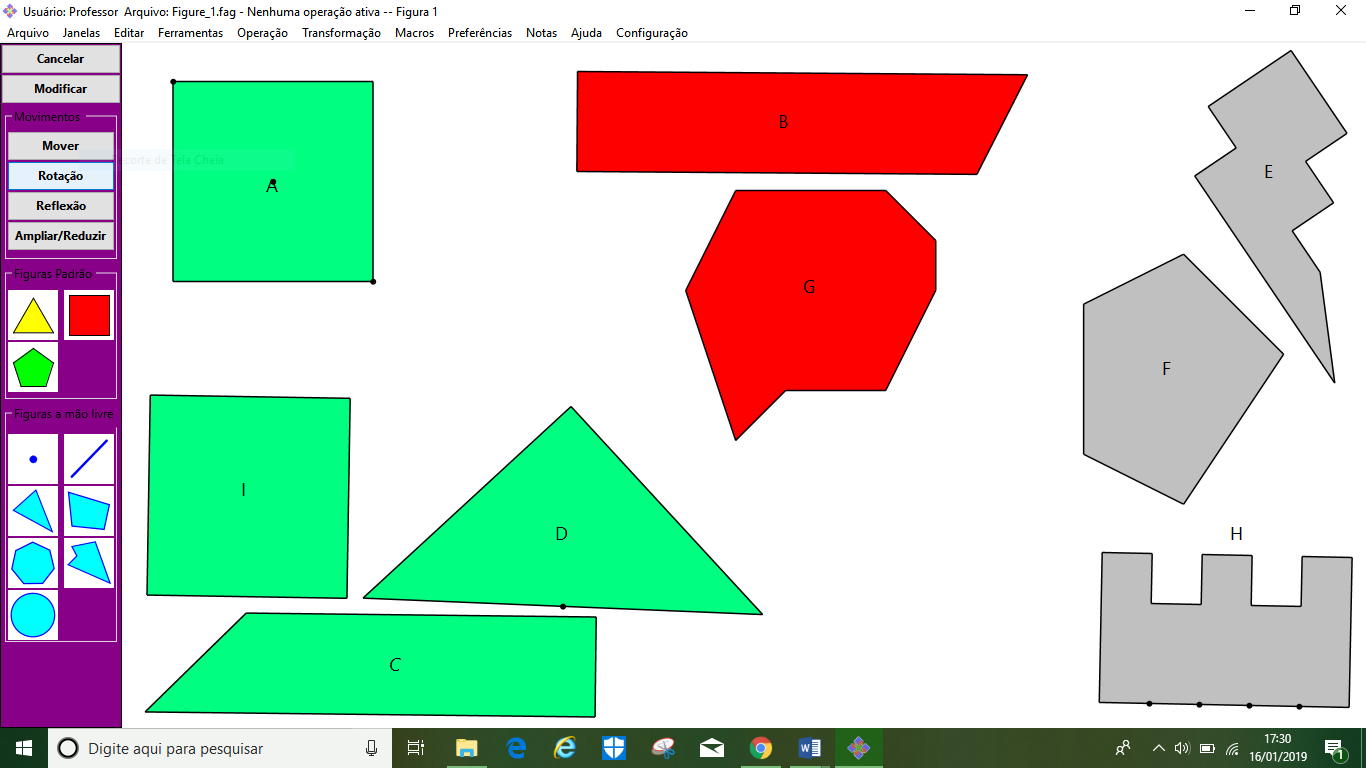
Após a conclusão da questão, os licenciandos sentiram a necessidade de expor algumas considerações de maneira escrita no word, explicando seus resultados. No documento do word, a dupla enfatizou que apenas as figuras C, D e I possuem a mesma área que a figura A. Para se chegar ao devido resultado, usaram conhecimentos matemáticos, como unidade de medida e conhecimentos geométricos de composição e decomposição de figuras.
Assim como na primeira questão, a segunda propôs um conjunto de figuras e se pediu que as comparassem com a figura A, identificando se possuem área maior, menor ou igual. Após terem mobilizado bastantes conhecimentos na primeira questão, os licenciandos já previram que utilizariam a unidade de medida e os procedimentos matemáticos de decomposição e recomposição de figuras planas, no qual de acordo com Baltar (1996) e Ferreira (2010) correspondem a associação entre os quadros numérico e geométrico.
Como uma forma de facilitar esses procedimentos, a dupla adotou o uso da malha quadriculada, para agilizar o processo de resolução e resposta correta.

Como produto final dos procedimentos adotados pelos licenciandos para se obter as respostas se tem, como mostra a Figura 17, que as figuras da cor azul possuem a mesma área que A, as figuras da cor rosa possuem área menor que A, e as figuras da cor amarela possuem área maior que A.
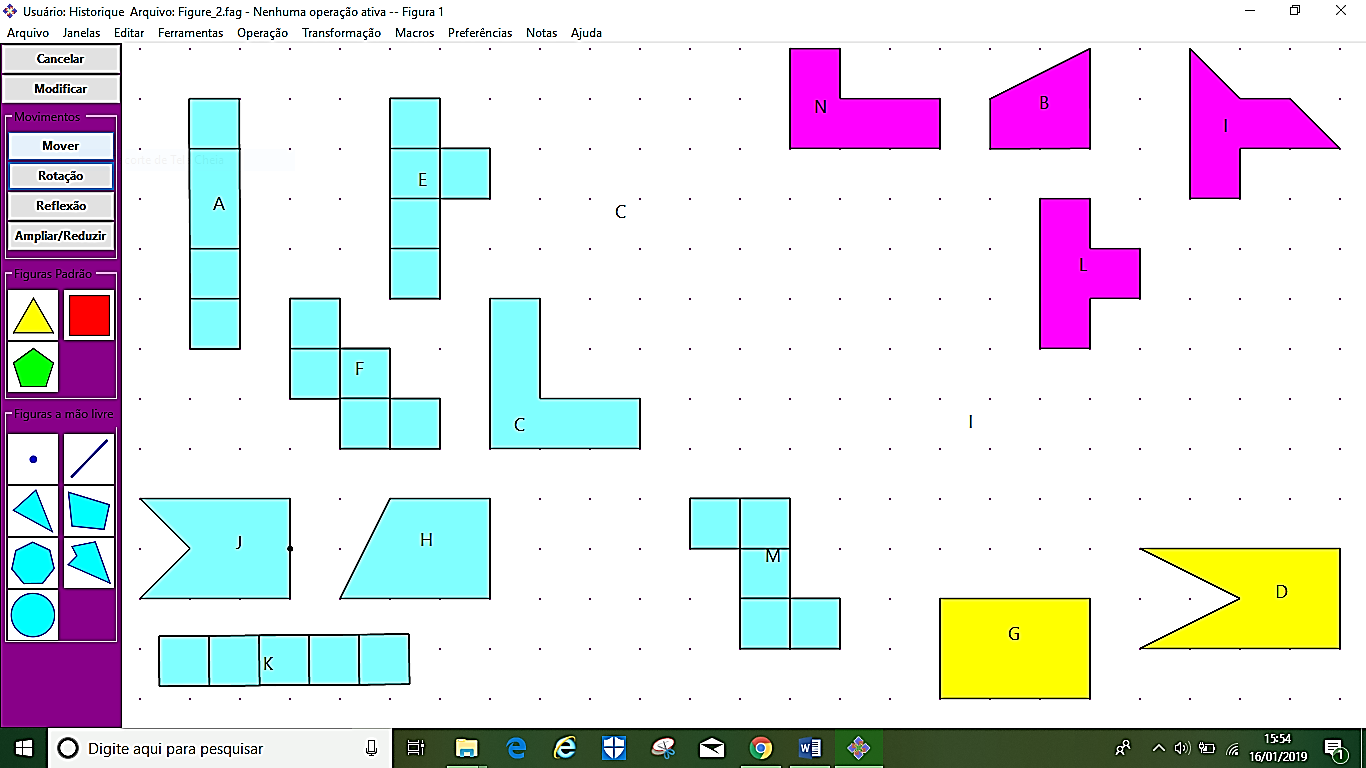
Os licenciandos optaram por usar o menu AC e apoiarem-se no uso da malha quadriculada para se obter as respostas da questão. No que se refere a resolução, foi adotado o processo de decomposição e recomposição nas figuras B, D, G, H e J. Para as demais figuras (C, E, F, I, K, L, M e N) o método usado foi o ladrilhamento efetivo.
Com base nas descrições propostas, se evidencia que o processo de Gênese Instrumental ocorreu, isto é, os licenciandos transformaram o artefato em instrumento, assim como, se apropriaram das ferramentas (malha quadriculada, mover, colorir, decompor, dividir, duplicar) que integram os menus AB e AC.
Os esquemas de utilizações foram perceptíveis em alguns momentos, entre eles: os EU foram notáveis quando os participantes usavam alguma ferramenta pré-definida para se obter algo (malha quadriculada, dividir, decompor e outras funcionalidades); os EAI ocorreram quando a dupla se apropriou de algumas funcionalidades (malha quadriculada, dividir, decompor e outras funcionalidades) constantes nos menus AB e AC para resolverem a atividade; por último, os EACI se tornou notável quando eles tinham que juntamente pensar em estratégias para se obter a resposta da atividade.
Se conclui, portanto, que a instrumentalização aconteceu no momento que a dupla manipulava o software e tentavam organizar suas ideias para resolver a atividade. Em outras palavras, a dupla se apropriou das ferramentas descritas anteriormente e associaram a elas conhecimentos matemáticos para resolver a atividade, em exceção da ferramenta colorir. Já a instrumentação ocorreu quando eles desenvolveram os esquemas de utilizações, transformando-o em ações práticas para obter o resultado da atividade.
5. CONSIDERAÇÕES
Apoiada sob a ótica da TI, em especial do processo de Gênese Instrumental, buscou-se responder, inicialmente, a primeira indagação de pesquisa: de que maneira dois licenciandos de matemática se instrumentalizaram com as ferramentas do Apprenti Géomètre 2 no estudo da comparação da área de figuras planas?
Os resultados obtidos evidenciaram as relações entre os três polos (Sujeito - Instrumento - Objeto) a partir do modelo SAI, e por meio das análises verificou-se que os participantes se instrumentalizaram de algumas ferramentas do Apprenti Géomètre 2 dos menus “AB” e “AC” (pois foram o que eles utilizaram), para o estudo da comparação da área de figuras planas. No entanto, isso condiz que eles também se instrumentalizaram das mesmas ferramentas (malha quadriculada, mover, colorir, decompor, dividir, duplicar) dos menus “A”, “B” e “C” isoladamente. No que se refere a instrumentação, nesse estudo, os resultados evidenciam que a dupla de licenciandos estão instrumentados com essas ferramentas descritas para resolver situações referentes a comparação de áreas.
Com base no segundo questionamento: Quais conhecimentos matemáticos foram mobilizados pelos participantes no ambiente da ferramenta tecnológica para resolução do estudo da comparação da área de figuras planas? Evidencia-se que os conhecimentos matemáticos que mais foram mobilizados pelos licenciandos no decorrer da resolução da atividade foram a sobreposição, inclusão, decomposição e recomposição de figuras planas, assim como, o ladrilhamento efetivo (realizando a contagem da unidade de medida adotada).
No que tange a terceira indagação: Qual (is) esquema (s) de utilização (ões), segundo a TI, é (são) evidenciado (s) no presente estudo? Obteve-se, por meio dos resultados, que o surgimento dos três esquemas de utilizações descritos por Rabardel (1995), ou seja, os EU, EAI e EACI, foram marcantes na associação entre as estratégias matemáticas e a utilização dos menus e ferramentas do Apprenti Géomètre 2.
Por meio destes resultados destaca-se que estudar a Gênese Instrumental é relevante, uma vez que, possibilita entender como pessoas se apropriam de um recurso (artefato) e o usa em situações práticas para obter um resultado, sendo fruto de ação.
Essa pesquisa alia-se a reflexão de que os processos de instrumentalização e instrumentação são relevantes antes mesmo do docente apresentar e usar um recurso tecnológico em sala de aula, pois ao passar por esses processos ele se apropria do artefato, transformando-o em instrumento. Dessa maneira, ele reconhece como, quando e porque usar aquele recurso em determinada aula, não faz isso aleatoriamente.
Se sugere para futuros textos que explorem a situação de comparação em distintos ambientes (tecnológico, malha e papel e lápis) e se faça a comparação de seus resultados. Outra sugestão para vindouras pesquisas é o de investigar por meio da Orquestração Instrumental (OI) como professores de matemática planejam, executam e avaliam a vivência de suas aulas sobre a grandeza área, mediante um ambiente orquestrado previamente a partir de sua experiência profissional.
REFERÊNCIAS
BALTAR, P. M. Enseignement et apprentissage de la notion d’aire de surfaces planes: une étude de l’acquisition des relations entre les longuers et les aires au collège. 1996. Tese (Doutorado em Didática da Matemática), Université Joseph Fourier, Grenoble, França, 1996.
BELLEMAIN, P.; LIMA, P. Um estudo da noção de grandeza e implicações no Ensino Fundamental. Ed. Geral: John A. Fossa. Natal: SBHMat, 2002.
DOUADY, R.; PERRIN-GLORIAN, M. J. Un processus d’apprentissage du concept d’aire de surface plane. Educational Studies in Mathematics. v.20, n.4, p. 1- 50, 1988.
FALZON, P. Natureza, objetivos e conhecimentos da ergonomia: elementos de uma análise cognitiva da prática. In: FALZON, P. (Org). Ergonomia. São Paulo: Editora Blucher, 2007.
RABARDEL, P. Les hommes et les technologies: une approche cognitive des instruments contemporains . Paris: Armand Colin, 1995.
PACHÊCO, F.F.F. O processo de gênese instrumental por licenciandos em matemática no estudo da grandeza área mediado com o Apprenti Géomètre 2: reflexões, limites e possibilidades. In: Anais... XXII Encontro Brasileiro de Estudantes de Pós-Graduação em Educação Matemática, 2018, Belo Horizonte - Minas Gerais, 2018. v. 1.
SILVA, A. D. P. R. Ensino e Aprendizagem de Área Como Grandeza Geométrica: um estudo por meio dos ambientes papel e lápis, materiais manipulativos e no apprenti géomètre 2 no 6º ano do ensino fundamental. 2016. 317 f. Dissertação (Educação Matemática e Tecnológica). Universidade Federal de Pernambuco, Centro de Educação. Recife, 2016.
Autor notes
Ligação alternative
https://periodicoscientificos.ufmt.br/ojs/index.php/reamec/article/view/7890 (pdf)

