



ANÁLISE PRAXEOLÓGICA DE DIRETRIZES CURRICULARES REFERENTE AO ESTUDO DE NÚMEROS BINÁRIOS
PRAXEOLOGICAL ANALYSIS OF CURRICULAR GUIDELINES CONCERNING THE STUDY OF BINARY NUMBERS
REAMEC – Rede Amazônica de Educação em Ciências e Matemática
Universidade Federal de Mato Grosso, Brasil
ISSN-e: 2318-6674
Periodicidade: Frecuencia continua
vol. 7, núm. 1, 2019
Recepção: 13 Setembro 2018
Aprovação: 01 Dezembro 2018
Resumo: Objetiva investigar a abordagem de números binários, a nível escolar, em diretrizes curriculares de Matemática e de Computação. Para tal, recorre à Teoria Antropológico do Didático como elemento teórico e, mais especificamente, a praxeologia como ferramenta de pesquisa. Não identifica abordagem de números binários em diretrizes curriculares internacionais de Matemática: Ontario (2005, 2007). No entanto, identifica abordagem de números binários em diretrizes curriculares internacionais de Computação: Ontario (2008, 2009) e Computer Science Teachers Association (2011). Os números binários configuram-se como tema ou setor de estudo necessário para a compreensão de outros saberes, próprio, da Computação. Identificamos dezesseis tipos de tarefas, duas técnicas e princípios de tecnologia nessas diretrizes curriculares internacionais de Computação.
Palavras-chave: Números Binários, Praxeologia, Diretrizes Curriculares, Ensino de Matemática, Ensino de Computação.
Abstract: It aims to investigate approach of binary numbers at the school level in curriculum guidelines of mathematics and computing. So it uses the Anthropological Theory of Didactic as a theoretical element and, more specifically, the praxeology as a research tool. It does not identify binary numbers in international math curriculum guidelines: Ontario (2005, 2007). However, it identifies the approach of binary numbers in international curriculum guidelines in computing: Ontario (2008, 2009) and Computer Science Teachers Association (2011). Binary numbers are configured as a theme or a sector of study necessary for the understanding of other knowledge, specific to computing. It identifies sixteen types of tasks, two technicals and principles of technology in these international computing curriculum guidelines.
Keywords: Binary numbers, Praxeology, Curriculum Guidelines, Mathematics Teaching, Computation Teaching.
1. INTRODUÇÃO
O sistema de numeração binário utiliza apenas dois dígitos, 0 ou 1, para representar um número. Já o sistema de numeração decimal utiliza dez dígitos ou algarismos, 0 a 9, para representar um número. Por exemplo, 1100 (um um zero zero) é um número representado no sistema binário; 12 (doze) é o mesmo número representado no sistema decimal:. Lê-se: um um zero zero na base 2 é igual a doze na base 10.
Os números binários constituem o lócus da “Era Digital”; são utilizados atualmente como elementos necessários e fundamentais na comunicação entre artefatos tecnológicos digitais por serem utilizados como representação de número (sequências de 0s e 1s) em codificações de caracteres, de vídeos, de sons, de qualquer outro tipo de dado. Qualquer artefato tecnológico digital, o computador, por exemplo, é composto por uma série de interruptores elétricos com duas posições. Por conversão, a chave na posição "1" significa está ligado e a chave na posição "0" significa que o interruptor está na posição desligado. A partir dos pulsos elétricos (on/off) o computador reescreve através de dígitos binários. Por exemplo, quando escrevemos a letra "H" o computador converte esta letra em dígitos binários ou código binário 0100.1000 de acordo com a tabela ASCII (American Standard Code Information Interchange).
Os números binários são estudados em cursos superiores de Ciências da Computação, Matemática, Engenharia entre outros, por disciplinas como Circuitos Digitais, Teoria dos Números, Comunicação de Dados, como exemplos. No entanto, a sua abordagem na Educação Básica seria coerente com os objetivos educacionais atuais firmados por este nível de ensino nos documentos educacionais oficiais? As diretrizes curriculares, nacionais e internacionais, recomendam o seu estudo na escola? Se sim, o que elas sugerem? Quais seriam as áreas de saber e blocos de conteúdos que sugerem o ensino de números binários na Educação Básica? A partir de que nível escolar as diretrizes curriculares sugerem o estudo de números binários?
Segundo Mendes (2014), as diretrizes curriculares nacionais de Matemática e estadual de Pernambuco não sugerem o estudo de números binários, enquanto sistema de numeração, como conteúdo básico de aprendizagem de Matemática em níveis de Ensino Fundamental e Ensino Médio. Entretanto, nas sugestões frente ao bloco de conteúdos Grandezas e Medidas do terceiro ciclo do Ensino Fundamental, é sugerida a abordagem de algumas unidades da informática como bytes, quilobytes, megabytes, gigabytes, em contextos apropriados, pela utilização da potenciação. Exemplos: “Quantos kilobytes de memória tem um computador com 2 gigabytes?” (ONAGA, MORI, 2012, p.24, ex: 59); “Em um pen drive, cuja capacidade de armazenamento é de 4GB, é possível armazenar: a) 1 arquivo de 5000MB; b) 12 arquivos de 372MB cada; c) 8 arquivos de 452MB cada; d) 1 filme de 3GB e 1 arquivo 1400MB”(PATARO, SOUZA, 2012, p.203, ex: 38).
Mendes (2016a) realizou análise praxeológica em livro didático escolar de Computação e constatou que os números binários são pré-requisitos ao estudo de codificação/decodificação, armazenamento, processamento, transmissão, detecção/correção de erros, compressão e medição de dados. Os números binários são utilizados como representação de dados.
Mendes (2017b) realizou análise praxeológica em uma coleção de livros didáticos de Matemática dos anos finais do Ensino Fundamental brasileiro e constatou que os números binários é um tema auxiliar ao estudo de potenciação e/ou é um tema de curiosidade no Manual do Professor.
A partir das pesquisas de Mendes (2014, 2016a, 2017b), objetivamos: investigar a abordagem de números binários, a nível escolar, em diretrizes curriculares (nacionais e internacionais) de Matemática e de Computação; verificar se existe sugestão de tarefas, de técnicas, de tecnologias e de teorias recorrentes ao estudo de números binários; verificar se os números binários constituem como saber básico escolar em diretrizes curriculares; identificar sugestões didáticas, pedagógicas referentes ao ensino de números binários; e identificar quais são os blocos de conteúdo que trabalham o estudo de números binários.
Recorremos à Teoria Antropológica do Didático (TAD) como elemento teórico e, mais especificamente, a praxeologia como ferramenta de pesquisa. Como ainda não é definida por lei uma disciplina própria que contempla saberes de Computação na Educação Básica brasileira, investigamos também a existência, ou não, de recomendações didáticas internacionais referentes ao ensino de números binários em diretrizes curriculares de Computação, correspondentes ao Ensino Fundamental e Ensino Médio.
2. REFERENCIAL TEÓRICO
A TAD defende a existência de elementos práticos e teóricos, de maneira imbricada, em qualquer que seja a ação humana. Esses elementos são advindos de pelo menos um questionamento, que são apoiados por elementos lógicos e teóricos entrelaçados. A partir disso, a TAD, mais especificamente, a praxeologia ou a organização praxeológica, defende a existência de justificativa e explicação de qualquer que seja a ação, o fazer humano.
A palavra praxeologia deriva de duas palavras gregas: práxis e logos. Práxis significa a parte prática da ação humana, enquanto o logos significa a parte inteligível, racional e lógico dessa ação humana que se configura a teoria (CHEVALLARD, 2005).
A TAD afirma que o funcionamento de instituições existe, e é necessário requerer uma organização praxeológica: tipos de tarefas, técnicas, tecnologias e teorias. Os tipos de tarefas constituem “fazer coisas”; as técnicas constituem o como fazer tarefas, essas coisas; as tecnologias constituem na justificativa e explicação da veracidade das técnicas para executar as tarefas; e as teorias constituem o porquê formal e lógico destas explicações e justificações. Ou seja, em qualquer instituição, seja ela uma igreja, uma família, uma escola ou outra qualquer, é possível, a partir da noção de praxeologia, analisar as transformações que o objeto de saber (Matemática, Computação, etc.) atua em uma instituição para outra (CHEVALLARD, 1998a).
Por exemplo: some os números binários: 110 e 11. Primeiro posicione cada dígito dos números, um em baixo do outro, a partir da direita para a esquerda. Segundo, passe um traço abaixo do segundo número e ponha o sinal “+” a direita ou a esquerda. Terceiro, some cada dígito, a partir da direita para a esquerda.
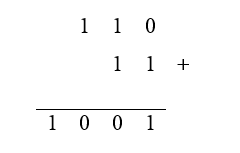
O procedimento de somar esses números binários - as três etapas - constitui a técnica utilizada para realizar o tipo de tarefa: somar dois números binários (110 e 11).
Uma pergunta poderia ser feita: Por que a segunda e terceira ordens são zeros?
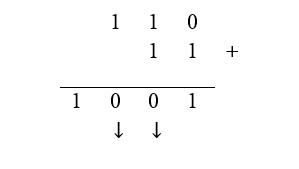
Por que são zeros?
Uma explicação para aquela pergunta poderia ser a seguinte: como no sistema binário apenas existem os dígitos 0 e 1, então o resultado da soma de cada dígito será 0 ou 1. No sistema binário não existe “2” como no sistema decimal. Além disso, 0 + 0 = 0; 0 + 1 = 1; 1 + 0 = 1 e 1 + 1 = 10 (um zero). Mas então, por que na 2ª ordem não ficou 10? Porque cada ordem apenas representa um único dígito ou algarismo, 0 ou 1. Portanto na 2ª ordem não podemos escrever 10 (um zero). Dessa maneira, a 2ª ordem fica 0 e a 3ª ordem fica 1, semelhante ao sistema decimal quando dizemos “vai a um”. Ou seja, 1 + 1 = 0 vai a 1 (este 1 vai ser somado ao algarismo da 3ª ordem). Além disso, a cada nova ordem ou algarismo acrescentado indica o dobro de representações do número escrito por quantidade de algarismos anterior. Exemplo: Um algarismo pode representar dois números binários: 0 ou 1; dois algarismos podem representar quatro números binários (dobro de duas representações): 00 ou 01 ou 10 ou 11; três algarismos podem representar oito números binários (dobro de quatro representações): 000 ou 001 ou 010 ou 011 ou 100 ou 101 ou 110 ou 111; e assim sucessivamente. Essas explicações constituem a tecnologia. Observe que a cada explicação dada existiram novos por quês. E a partir dessa explicação mais formal dos por quês, aprofundada por teoremas, generalizações, conceitos de numeral, número, etc. Configura-se o último elemento de praxeologia: teoria. Portanto, o discurso tecnológico contém afirmações que pode conter por quês. E a teoria aparece como sendo as respostas dadas a esses por quês, ao maior nível de explicação dela (CHEVALLARD, 1998a), sendo um [...] “conjunto mais abstrato de conceitos e argumentos dispostos em um discurso geral que justifica a tecnologia em si” (MARTENSEN, 2011, p.218).
A TAD define o trabalho do objeto O (Matemática, Computação, etc.) como sendo um trabalho combinado de elementos praxeológicos (tarefas, técnicas, tecnologias e teorias) que por sinal, nem sempre são claros e identificados em determinada instituição. Didaticamente, o estudo do objeto de saber O consiste em providenciar alguma análise praxeológica (didática) de O. Exemplo: a tarefa é contextualizada? Como executar a tarefa por essa técnica? A técnica é justificada e explicada? A veracidade da técnica é teorizada? Assim, qualquer análise didática implica alguma (re)formulação de organização praxeológica de O.
Primeiro as instituições transpositivas (diretrizes curriculares, sindicatos, programas, especialistas, etc.) definem, de maneira conjunta e interdependente, qual será o objeto de saber a ser ensinado e aprendido em determinada instituição. Ou seja, primeiro as instituições transpositivas - as diretrizes curriculares neste nosso trabalho - definirão as praxeologias Matemática e Computação, o que será estudado em instituições de ensino escolar, já criadas, trabalhadas pelo saber científico, acadêmico. A partir dessa definição, as diretrizes curriculares enfatizarão, em parcerias e interdependências entre elas, o trabalho transpositivo (praxeologia didática) como sendo uma oportunidade para retrabalhar as praxeologias Matemática e Computação ao ponto de (re)adaptá-las às novas condições institucionais (melhorar as praxeologias), às condições econômicas, sociais, etc.
Chevallard (1998b) distingue três tipos de saber: saber científico (cientistas e academia), saber a ensinar (noosfera: autores de livros, programas, diretrizes curriculares, programas, sindicato, etc.) e o saber ensinado (esfera: escola). Então, a transposição didática permite transpor o saber de uma instituição (científica) para outra instituição (escolar) sendo que cada instituição trata o saber de sua maneira. O saber científico, o saber a ser ensinado e o saber ensinado possuem naturezas diferentes segundo a teoria da transposição didática de Chevallard (1998b); o tratamento com o saber em instituições acadêmicas, transpositivas e escolares é diferenciada. Nessa mediação entre saber científico e saber ensinado existe o saber a ser ensinado que se configura com o trabalho transpositivo das diretrizes curriculares, por exemplo, a fim de sugerir, auxiliar, guiar, orientar o trabalho, a avaliação, a prática pedagógica de determinado objeto de saber O em diversas instituições de ensino.
A praxeologia é constituída por um bloco prático-técnico e por um bloco tecnológico-teórico (CHEVALLARD, 2013). Segundo Chevallard (1998a) o primeiro bloco é normalmente identificado como conhecimento, enquanto que o segundo bloco é normalmente identificado como saber (científico).
No caso da praxeologia O existem momentos que um sujeito x encontra-se um tipo de tarefa e, em seguida, necessita-se de pelo menos uma técnica, para executá-la (bloco prático-técnico). Por conseguinte, existe pelo menos uma explicação e justificativa – elementos tecnológicos – que valida, teoriza a técnica utilizada (bloco tecnológico-teórico) (CHEVALLARD, 1998a).
Chevallard (1998a) define quatro categorias de organizações praxeológicas: praxeologia pontual, praxeologia local, praxeologia regional e praxeologia global. A praxeologia pontual é definida a partir de um tipo de tarefa, uma técnica, uma tecnologia e uma teoria. Ela é assim categorizada quando apenas leva em consideração um único tipo de tarefa. A praxeologia local é assim categorizada quando leva em consideração uma determinada tecnologia. A praxeologia regional é desenvolvida em torno de uma única teoria; é composta por várias tecnologias, que cada qual por sua vez, justifica e explica às várias técnicas correspondentes ao maior número de tipos de tarefas. A praxeologia global é a agregação de várias organizações praxeológicas regionais atuantes às várias teorias.
3. ANÁLISE PRAXEOLÓGICA DE DIRETRIZES CURRICULARES REFERENTES AO ESTUDO DE NÚMEROS BINÁRIOS
Analisamos as organizações praxeológicas referentes ao estudo de números binários em diretrizes curriculares nacionais e internacionais de Matemática e de Computação. Ou seja, primeiro verificamos se os números binários constituem um saber básico escolar. Caso afirmativo, investigamos a existência, ou não, de sugestões de tarefas, de técnicas, de tecnologias e de teorias. Em paralelo, identificamos, ou não, sugestões, orientações didáticas, pedagógicas referentes ao ensino de números binários.
A partir das análises praxeológicas Matemática e Computação, configuramos as diretrizes curriculares (nacionais e internacionais) em praxeologia pontual ou praxeologia local ou praxeologia regional ou praxeologia global. A partir dessas denominações de praxeologia, constatamos, ou não, se o objeto de saber, números binários, foi abordado no bloco prático-técnico e/ou no bloco tecnológico-teórico; identificamos quais são os blocos de conteúdo que trabalham o estudo de números binários e como eles são articulados com/por meio do objeto do saber números binários.
Cada análise praxeológica Matemática e praxeológica Computação em diretrizes curriculares foi organizada por meio de seções e subseções. Cada seção apresentou a análise praxeológica de diretrizes curriculares nacionais e internacionais de maneira conjunta, porém organizadas por áreas de saber: análise praxeológica de diretrizes curriculares de Matemática e análise praxeológica de diretrizes curriculares de Computação. Cada subseção referenciou a cada instituição diretiva curricular analisada – diretrizes curriculares de determinado país. Depois das análises praxeológicas Matemática e Computação referentes ao estudo de números binários, mostramos e discutimos os resultados de pesquisa.
Para delimitar este trabalho, investigamos a existência, ou não, de sugestões referentes ao estudo de números binários em diretrizes curriculares internacionais de Matemática e de Computação referentes ao Ensino Fundamental e Ensino Médio: Parâmetros Curriculares Nacionais (PCN) de Matemática (BRASIL, 1997, 1998, 2000) e do estado de Pernambuco (PERNAMBUCO, 2012); UNESCO (1997), Computer Science Teachers Association (CSTA,2011) e Ontario (2005, 2007, 2008, 2009).
Ressaltamos que as diretrizes curriculares de informática para a Educação Básica da UNESCO (1997), apesar de ser internacional, foi uma parceria com a Secretaria de Educação a Distância do Ministério da Educação (MEC) e a Universidade de Brasília (UNB), por intermédio de seu departamento de Ciência da Computação.
Esta pesquisa é documental, que do ponto de vista teórico e de ferramenta de análise de pesquisa, utiliza-se a praxeologia (TAD).
3.1. Análise praxeológica de diretrizes curriculares de Matemática
Baseado nos conceitos da TAD, Mendes (2014) identificou em diretrizes curriculares oficiais nacionais e estadual (Pernambuco) de Matemática quatro tipos de tarefas a ser estudado: reconhecer a capacidade de memória do computador como uma grandeza; identificar unidades de medidas da informática, como: bytes, quilobytes, megabyte e gigabytes; usar unidades de medida da informática; e converter unidades de medida da informática. Porém, Mendes (2014), não identificou orientações didáticas referentes ao estudo de sistema de numeração binário.
Segundo Mendes (2014), o estudo de unidades de medidas da informática, são abordados a partir dos anos finais do Ensino Fundamental, e partir deste nível de ensino, as diretrizes curriculares nacionais de Matemática definem expectativas de aprendizagem (sugere o mínimo que o estudante deve aprender para desenvolver as competências básicas na disciplina): unidades de medida (do sistema métrico decimal) de informação: bytes, quilobytes, megabytes e gigabytes. Portanto, as unidades de medidas da informática caracterizam-se como "piso" de aprendizagem em nível de Ensino Fundamental. A diretriz curricular nacional de Matemática, Brasil (1998, ibidem, p.69), argumenta que “o estudo de diferentes grandezas, de sua utilização no contexto social [...] está fortemente conectado com diferentes tipos de números”.
Segundo Mendes (2014), as diretrizes curriculares de Matemática escolar baseiam-se na construção de competências básicas, de maneira reflexiva, sobre os conhecimentos dessa construção pelos próprios estudantes. Estes sendo levados a “fazer Matemática”, podendo-se utilizar recursos - artefatos tecnológicos (internet, computador, calculadoras, entre outros). O estudo de unidades de medida da informática “dependendo das condições de cada sala de aula, elas podem ser ampliadas e/ou aprofundadas" (PERNAMBUCO, 2012, p.13). Uma vez que, os alunos e as alunas possuem conhecimentos prévios e/ou contato com algumas grandezas e medidas.
Segundo Mendes (2014), a abordagem de números binários em diretrizes curriculares de Matemática nacionais e estadual de Pernambuco gira em torno das necessidades de ligação do estudo das grandezas e medidas à situação do cotidiano do estudante. Para tal, sugerem: articular o estudo por meio de jogos (jogo do Nim, jogo HEX, entre outros); contextualizar os conceitos (matemáticos) ao processo de evolução histórica, evidenciando a articulação do objeto do saber (Matemática) com as necessidades humanas de cada época ao invés, apenas, de descrever os fatos ocorridos no passado ou a atuação de personagens que se destacaram na história humana; ampliar a dimensão lúdica do discente.
Em relação às diretrizes curriculares internacionais de Matemática, Ontario (2005, 2007), não identificamos recomendações referentes ao estudo de números binários.
3.2. Análise praxeológica de diretrizes curriculares de computação
A Sociedade Brasileira de Computação (SBC), assim como a Associação de Professores de Ciência da Computação dos Estados Unidos (CSTA, 2011), defendem o ensino de Ciência da Computação, como integrante das ciências, desde o ensino fundamental, como disciplina própria, assim como atualmente são consideradas a Matemática, a Física, a Biologia, etc. No entanto, referente ao estudo de números binários, não identificamos nenhum elemento praxeológico e nem tão pouco sugestões didáticas em diretrizes curriculares nacionais de Computação a nível escolar (Ensino Fundamental e Ensino Médio), apesar de existir uma tradução em português de livro didático de Ciência da Computação, Bell (2011), que aborda números binários por meio de representação de dados como armazenamento, transmissão, detecção e correção de erros, compressão, codificação e medição de informação (MENDES, 2016a).
A seguir, analisamos as organizações praxeológica Computação referentes ao estudo de números binários das seguintes diretrizes curriculares internacionais de Computação: CSTA (2011), UNESCO (1997), e Ontario (2008, 2009).
3.2.1. Diretriz Curricular de Computer Science Teachers Association
A Computer Science Teachers Association (CSTA, 2011) elaborou um documento contendo normas integradas para a educação de Ciência da Computação em nível escolar. Define 3 níveis de estudo em Ciência da Computação: o nível 1 destina-se ao k-6. O nível 2 destina-se ao grau 6 a 9 e o nível 3 destina-se aos estudantes do grau 9 a 12. Este último nível divide-se em 3 campos diferentes: “Ciência da Computação no mundo moderno” (nível 3A), “Conceitos e práticas das Ciências da Computação” (nível 3B) e “Temas em Ciências da Computação” (nível 3C). Abrangendo desta maneira três domínios da Computação: Educação Tecnológica (uso de computadores e outros artefatos tecnológicos de computação), Informação Tecnológica (organização de infraestrutura, desenho, administração de artefatos tecnológicos) e Ciência da Computação (CS) (“é o estudo dos computadores e dos processos algoritmos, incluindo seus princípios, seus desenhos de hardware e software, suas aplicações e seu impacto na sociedade”) (CSTA, 2011, p.6).
A CSTA (2011) define objetivos para os estudantes de Ciência da Computação no k-12 que abrangem cinco competências: pensamento computacional; colaboração; prática de Computação e programação; computadores e dispositivos de comunicação; e impactos globais, éticos e a comunidade. Para atender as metas desta pesquisa, apenas especificaremos, os objetivos propostos pela CSTA (2011) relacionados aos números binários por seu respectivo nível de estudo e grau escolar. “O estudante será capaz de”:
- “Demonstrar como uma sequência de bits pode ser utilizada para representar a informação alfanumérica” (ibidem, p.13). Nível 1. Grau escolar k-3;
- “Representar os dados de várias maneiras, incluindo textos, sons, imagens e números” (ibidem, p.17). Nível 2. Grau escolar k 6-9.
- “Examinar as conexões entre os elementos das matemáticas e das ciências da computação, incluindo os números binários, lógica, conjunto e funções” (ibidem, p.17). Nível 2. Grau escolar k 6-9.
- “Descrever a relação entre as representações binárias e hexadecimais” (ibidem, p.18). Nível 3A. Grau escolar 9º e 10º.
- “Explicar os princípios de segurança examinando a codificação, a criptografia e as técnicas de autenticação” (ibidem, p.19). Nível 3A. Grau escolar 9º e 10º.
- “Descrever como se utilizam as funções matemática e estatística, os conjuntos e a lógica na computação” (ibidem, p.19). Nível 3A. Grau escolar 9º e 10º.
- “Discutir a interpretação de sequências binárias em uma variedade de formas (por exemplo, instrução, números, texto, som, imagem)” (ibidem, p.20). Nível 3B. Grau escolar 10º a 12º.
Baseado nos conceitos da TAD, nas normas de implementação curricular de Computação à Educação Básica da CSTA (2011), nesta, há uma única técnica, sugestões de tarefas e um princípio de tecnologia, mas não há sugestões de teoria. Identificamos 7 tipos de tarefas referentes aos números binários:
- Tipo de tarefa T1: utilizar 0s e 1s para representar imagens, presente na atividade “Colorir com números”, página 29. Ela é baseada na atividade “Colorindo com Números” trabalhada na página 15 do livro de Bell e seus colaboradores (BELL et al, 2011);
- Tipo de tarefa T2: codificar textos utilizando os métodos de folha de cálculos e de ASCII;
- Tipo de tarefa T3: decodificar textos utilizando os métodos da folha de cálculos e da tabela ASCII;
- Tipo de tarefa T4: discutir os tipos de textos e de imagens que se comprimem melhor/pior;
- Tipo de tarefa T5: converter um número representado no sistema binário em um número representado no sistema decimal;
- Tipo de tarefa T6: converter um número representado no sistema decimal em um número representado no sistema binário;
- Tipo de tarefa T7: contar, por meio do sistema binário, utilizando os dedos das mãos.
Todos aqueles tipos de tarefas estão presentes na atividade “Sistemas Numéricos”. A elaboração desses tipos de tarefas parte da seguinte justificativa (tecnologia): “os computadores não podem pensar como nós, necessitam de um código para transformar a nossa linguagem em dados tal que eles possam ser processados e convertidos para a linguagem reconhecida” (CSTA, 2011, p.39, tradução nossa).
Interpretamos a execução daqueles tipos de tarefa por meio de 3 etapas (praxeologia Didática): primeiro, sugere vídeos relacionados à “viagem ao interior de um computador” que mostre como os computadores representam imagens em códigos binários, percebendo a compreensão da informação, que é comunicada, representada pela necessidade de um código; segundo, apresenta um desafio aos estudantes para afirmar se é possível contar mais que 10, a partir dos dedos das duas mãos (atividade baseada em Bell et al (2011, p.10) que recorre da representação do dedo levantado correspondente a 1 e o dedo abaixado correspondente a 0). Para auxiliar esse desafio, primeiro é sugerido o estudo de circuitos lógicos simples a partir dos estados lógicos binários conjuntamente com a condição de série de circuitos lógicos combinacionais de lâmpadas, acessas e apagadas; segundo, trabalhar, de fato, a atividade de contar com os dedos das mãos até 31; terceiro, realizar a execução de tarefas para converter números representados nos sistemas binário e decimal e codificar/decodificar textos a partir da tabela ASCII em linguagem coloquial (vice-versa).
Apenas identificamos uma única técnica. Esta é para executar o tipo de tarefa T1 (utilizar 0s e 1s para representar imagens), porém ela é apresentada de maneira superficial e sem exemplos: a codificação da imagem é proporcionada mediante o escaneamento das sequências de 1s (quadrados pretos) e 0s (quadrados não pretos), em cada linha quadriculada, e o registro do comprimento de cada sequência.
3.2.2. Diretriz curricular da UNESCO
A Organização das Nações Unidas para a Educação, a Ciência e a Cultura (UNESCO, 1997), por meio da Federação Internacional de Processamento da Informação (IFIP), elaborou um currículo de informática para os anos finais do Ensino Fundamental e Ensino Médio não só para os seus países integrantes, mas também para atender a todos os demais países do mundo.
A Secretaria de Educação a Distância do MEC conjuntamente com Universidade de Brasília, por intermédio de seu Departamento de Computação, mantiveram parceria com a UNESCO nessa iniciativa de trabalhar a informática na educação brasileira.
Apesar da UNESCO (1997) não mencionar os números binários em sua proposta curricular de informática para a Educação Básica, há uma abordagem implícita deles uma vez que é proposto aos estudantes identificarem e entenderem os elementos básicos de hardware e o seu funcionamento (circuitos combinacionais, entrada, saída e processamento de dados, etc.), assim como devem entender a evolução dos computadores (parte histórica do computador) que provavelmente irão estudar, entre outras coisas, a performance da capacidade de armazenamento e processamento de dados e redução de tamanho do dispositivo de memória. Ou seja, é plausível que estudem números binários tanto por meio do sistema de numeração binário, como por meio das unidades de memória de computadores.
Baseado nos conceitos da TAD, a UNESCO (1997) apresenta temas e setores a respeito do estudo de Computação: banco de dados, tendências em Computação, hardware, entre outros. Em relação à organização praxeológica Computação, frente ao estudo de números binários, não sugere e nem esclarece nenhum elemento praxeológico: tarefa, técnica, tecnologia e teoria.
3.2.3. Diretrizes curriculares de Ontario (Canadá)
A diretriz curricular de Computação de Ontario (2008), programa 11 (equivalente ao 2º ano do Ensino Médio brasileiro), referente ao estudo de números binários, objetiva: “demonstrar uma compreensão de como o computador usa vários sistemas (por exemplo, binário, hexadecimal, ASCII, Unicode) para representar internamente dados e informações da loja” (ONTARIO, 2008, p.42, tradução nossa).
A diretriz curricular de Ontario, grau 9 e 10, referente à Educação Informática, estabelece, entre outros objetivos, “demonstrar conhecimentos básicos de números binários e lógica digital” (ONTARIO, 2009, p.58, tradução nossa).
A diretriz curricular de Ontario, grau 11 e 12, referente à Educação Informática, estabelece, entre outros objetivos, “demonstrar conhecimento de números binários, números hexadecimais, e álgebra booleana em lógica de computadores e processamento de dados” (ONTARIO, 2009, p.78, tradução nossa).
Identificamos recomendações referentes ao estudo de números binários na Educação Básica de Ontário (2008, 2009), mais especificamente, nas disciplinas Educação Informática e Tecnologias da Computação. Enquanto aos documentos curriculares de Matemática de Ontario (2005, 2007), não identificamos recomendações referentes ao estudo de números binários. A partir disso, interpretamos que os números binários são definidos em Ontario como tema ou setor de estudo da “disciplina Computação” e não da disciplina Matemática.
As diretrizes curriculares de Computação de Ontario (2008, 2009), mais especificamente referente ao estudo de números binários, não é fundamentada por nenhum elemento tecnológico-teórico. Apenas elabora tipos de tarefas e uma única técnica. Identificamos onze tipos de tarefas:
- T1: converter um número representado no sistema de numeração binário em um número representado no sistema de numeração decimal;
- T2: converter um número representado no sistema de numeração decimal em um número representado no sistema de numeração binário;
- T3: descrever como os computadores representam dados por meio de dígitos binários (códigos binários, ASCII);
- T4: descrever como é realizado o processamento de dados de um computador;
- T5: representar tabelas verdade a partir de portas lógicas;
- T6: representar expressões booleanas a partir de portas lógicas;
- T7: representar números inteiros como números binários;
- T8: representar números racionais como números binários;
- T9: transformar um número representado no sistema de numeração hexadecimal em um número representado no sistema de numeração binário;
- T10: transformar um número representado no sistema de numeração binário em um número representado no sistema de numeração hexadecimal;
- T11: relacionar expressões booleanas a portas lógicas por meio de representações de símbolos, de números e de expressões.
A diretriz curricular de Ontario exemplifica uma única técnica para ensinar números binários: o jogo de “cadeiras binárias”. Esta técnica é apresentada para executar o tipo de tarefa 3 (descrever como os computadores representam dados por meio de dígitos binários). Ela utiliza elementos sinestésicos: considere que “[...] oito estudantes representam um byte de dados por sessão ou em pé em frente de oito cadeiras, dependendo se eles representam binário 0 (sentado) ou binário 1 (em pé)” (ONTARIO, 2008, p.20, tradução nossa). Esta técnica não é exemplificada.
4. RESULTADOS E DISCUSSÃO
Constatamos que o bloco prático-técnico teve uma maior visibilidade que o bloco tecnológico-teórico referente ao estudo de números binários em diretrizes curriculares tanto na área de Matemática como também na área de Computação.
Identificamos dezesseis tipos de tarefas, duas técnicas e nenhuma tecnologia e teoria referentes ao estudo de números binários em diretrizes curriculares internacionais de Computação. Segundo Chevallard (1998a), mesmo a organização praxeológica pontual geralmente não é totalmente definida estruturalmente como: a técnica como sendo a forma de fazer, de realizar determinada tarefa, a tecnologia como sendo a justificativa e explicação dessa técnica utilizada para fazer essa tarefa e que a teoria como sendo o porquê desta justificativa funcionar perfeitamente. Ou seja, esses elementos de organização praxeológica podem não ser tão bem definidos, perceptíveis na prática.
“O tipo de tarefa em torno do qual foi constituída uma praxeologia pode não estar bem identificado, a técnica associada pode se revelar impraticável. A tecnologia pode, por vezes, ser reduzida a uma pura declaração de princípios e a teoria, pode ser perfeitamente enigmática” (CHEVALLARD, 1998a, p.6 tradução nossa).
Assim, a teoria pode não estar explicitada, assim como a tecnologia, a técnica...
Este trabalho, portanto pode servir de exemplificação teórica de praxeologia em que os seus elementos: tecnologia e teoria não estão presentes e que as técnicas identificadas não apresentam ilustrações de como se procedem as técnicas utilizadas para executar a representação de dados por meio de dígitos binários.
Apesar de as diretrizes curriculares nacional e estadual de Pernambuco de matemática (Brasil 1998; Pernambuco, 2012) sugerirem o estudo de unidades de medidas da Informática a partir do Ensino Fundamental por meio do sistema métrico decimal: quilobyte, megabyte e gigabyte (tal que a base numérica definida é a base 10 – sistema de numeração decimal) essa definição numérica e parte literal de medida, prefixos e os nomes das unidades de medida da informática estão equivocadas baseadas nas recomendações de normas técnicas do Sistema Internacional de Unidades (SI, 2012) e da Commission Electrotechnique Internationale (CEI, 2005) porque as medidas utilizadas na Informática: utilizam-se a base 2 – sistema binário – e não a base 10 como recomendadas por aquelas diretrizes curriculares nacionais de Matemática; apresentam suas próprias nomenclaturas e símbolos (parte literal da medida) conforme apresentado por SI (2012):
Os prefixos SI representam exclusivamente potências de 10 e não devem ser utilizados para expressar potências de 2 (por exemplo, um kilobit representa 1000 bits e não 1024 bits). Os prefixos adotados pela IEC para as potências binárias são publicados na norma internacional IEC[2] 60027-2: 2005, 3ª edição, símbolos literais para utilização em eletrotécnica - Parte 2: Telecomunicações e eletrônica. Os nomes e símbolos dos prefixos correspondentes a são, respectivamente: kibi, Ki; mébi, Mi; gibi, Gi; tébi, Ti; pébi, Pi; e exbi, Ei. Assim, por exemplo, um kibibyte se escreve: 1 KiB = B = 1024 B, onde B designa um byte. Ainda que esses prefixos não pertençam ao SI, eles devem ser utilizados na informática, a fim de evitar o uso incorreto dos prefixos SI (SI, 2012, p.34).
Portanto, 1 quilobyte (1 KB) é igual a 1 mil byte, enquanto que 1 kibibyte (1 KiB) é igual a 1024 bytes[3]. Assim como 1 megabyte (1 MB) é igual a 1 mil quilobyte e 1 mébibyte
(1 MiB) é igual a 1024 kibibytes. Aqueles equívocos de nomenclaturas e de símbolos de medidas da Informática também foram diagnosticados por Mendes (2016b) em livros didáticos de Matemática analisados pelo Programa Nacional de Livro Didático (PNLD).
As diretrizes curriculares de Computação a nível internacional, (CSTA, 2011; ONTARIO, 2008, 2009, 2011), defendem o estudo de números binários na escola. Inclusive, elas introduzem outros temas, setores e domínios de estudo referentes à Computação na Educação Básica. Já a nível escolar nacional, não identificamos nenhuma diretriz curricular de Computação.
As recomendações curriculares de Matemática nacionais e estadual de Pernambuco, referentes ao estudo de números binários, não abordam o sistema de numeração binário (BRASIL, 1997, 1998, 2000) e Pernambuco (2012).
Brasil (1998) recomenda o estudo de unidades de medida da informática voltado à prática social e ao auxílio da aprendizagem de potenciação.
Em relação às diretrizes curriculares de Matemática internacionais, não identificamos nenhuma praxeologia Matemática referente ao estudo de números binários a partir de Ontario (2005, 2007). De maneira diferente, as recomendações curriculares de Computação de Ontario (2008,2009), assim como as orientações curriculares de CSTA (2011) e SBC (1999): consideram os números binários como um tema ou setor fundamental de estudo escolar de Computação; recomendam um estudo intracomputação[4].
Identificamos que o sistema de numeração binário configura-se como um saber de estudo sugerido em diretrizes curriculares de Computação e não em diretrizes curriculares de Matemática, apesar desse saber ser criado na ciência Matemática (GLASER, 1981).
Em relação à abordagem de números binários em livros didáticos escolares avaliados pelo PNLD, Mendes (2018) concluiu que a abordagem de números binários é mais ampla e aprofundada em livro didático de Ciência da Computação que em livros didáticos de Matemática a partir de comparação de abordagem (análise praxeológica) de estudo de números binários em livros didáticos de Computação e de Matemática nacionais. Mendes (2018) constatou que os números binários configuram-se como um saber secundário na maioria dos livros didáticos de Matemática analisados: os números binários auxiliam o ensino e aprendizagem de potenciação ou são configurados como um tema de curiosidade no Manual do Professor.
A partir dos resultados desta pesquisa e de Mendes (2018), somos levados a fazer o seguinte questionamento: Os números binários apesar de serem um saber criado na ciência Matemática (GLASER, 1981) e estudado em várias ciências, Computação, Engenharia, etc. Eles tendem a ser configurado como um saber de estudo escolar de Computação e não mais um saber de estudo escolar de Matemática?
Decorrentes dos resultados desta pesquisa e de Mendes (2018), somos levados a retomar como apoio teórico a TAD para melhor compreendê-lo. Caso aquele questionamento seja afirmado, Chevallard (2005) explica que modelos generalizados de praxeologias podem ser destruídas, migradas, mudadas, desaparecidas, (re)surgidas, evoluídas, modificadas dentro de alguma instituição, a depender dos tipos de condições, restrições, limitações que norteiam as escolhas/decisões realizadas em termos de praxeologia Computação, Matemática, etc. Ou seja, as instituições transpositivas podem determinar o que/como/onde/quando/ por que será, ou não, ensinado determinado saber na escola.
Por um olhar exógeno à instituição escolar, todas as diretrizes curriculares internacionais de Computação analisadas, UNESCO (1997), ONTARIO (2008, 2009, 2011) e CSTA (2011), são unânimes ao incentivar a construção de uma disciplina própria na escola que contemple saberes de Computação. Essas duas últimas diretrizes curriculares mantêm os números binários como saber elementar inserida nessa disciplina, tal que os saberes dessa disciplina sejam: relacionadas com outras áreas e disciplinas; usem métodos e técnicas com/por meio de/utilização de artefatos tecnológicos (como o computador, principalmente).
Ainda por um olhar exógeno à escola, aquelas diretrizes curriculares internacionais de Computação, UNESCO (1997), ONTARIO (2008, 2009, 2011) e CSTA (2011), mantêm um discurso político em incentivar o aumento de profissionais de Ciência da Computação no país (assim como constatado por Feaster et al (2013) nos Estados Unidos) porque consideram o saber básico de Computação como fundamento essencial, assim como a leitura e a escrita, para uma melhor desenvoltura do cidadão no século XXI. Uma vez que partem da argumentação de que o pensamento computacional[5] é importante não apenas para conviver como cidadão consciente, hábil às performances tecnológicas necessárias para atender as exigências perpassadas por seu contexto cultural atual (inúmeras habilidades necessárias para compor o exercício da cidadania, como sujeitos autônomos, reflexivos e integrantes, mas conscientes, da importância do acesso, do manejo e articulação dos artefatos tecnológicos), mas também porque pode auxiliar no sistema cognitivo e operacional humano, por meio do acesso aos computadores (em redes), aumentando assim a produtividade, a criatividade, a performance cognitiva e operacional. Ou ainda, por “aprimorar o raciocínio computacional das crianças, pelo seu caráter transversal a todas as ciências” (FRANÇA et al, 2011, p.2).
Portanto, as diretrizes curriculares de Computação em nível internacional giram em torno do discurso voltado para: melhorar a compreensão púbica de Computação como campo acadêmico e profissional; incentivar a aprendizagem e o ensino desta área, a partir da educação escolar. Ou seja, as diretrizes curriculares de Computação UNESCO (1997), ONTARIO (2008, 2009, 2011) e CSTA (2011) defendem a implementação de um currículo escolar básico voltado para o estudo de saberes da Computação a partir de uma disciplina escolar própria assim como os já são em disciplinas Português, História, etc. Para suprir a falta de profissionais qualificados em informática; para alavancar o potencial econômico, científico do país; para desenvolver habilidades e conhecimentos tecnológicos de forma que possibilite o cidadão do século XXI ter uma melhor atuação em sua vida profissional e estudantil.
A partir dos resultados mencionados, este trabalho mostra-se relevante para o conhecimento da professora e do professor do ensino escolar atual porque os números binários podem ser um saber elementar para a compreensão funcional de outros saberes da Computação, como o funcionamento de artefatos tecnológicos digitais, por exemplo; podem servir como um objeto de saber auxiliar, transversal, ao entendimento de outras ciências; podem auxiliar o pensamento computacional, segundo a Computer Science Unplugger: “o sistema de numeração binário desempenha um papel central na forma como as informações de todos os tipos são armazenadas em computadores. Compreender binário pode levantar um monte de mistério a partir de computadores” (csunplugger.org/binary-numbers).
5. CONCLUSÃO
Concluímos que as organizações praxeológicas Computação referentes ao estudo de números binários nas diretrizes curriculares internacionais de Computação, Ontario (2008,2009) e CSTA (2011), caracterizam-se como sendo uma praxeologia local que trabalha apenas o bloco prático-técnico: identificamos dezesseis tipos de tarefas; duas técnicas, uma em Ontario (2008), técnica 1, e outra em CSTA (2011), técnica 2. Não identificamos nenhum elemento tecnológico-teórico. Não identificamos nenhum elemento de praxeologia Computação em UNESCO (1997). Não identificamos nenhuma diretriz curricular escolar nacional de Computação.
Os dezesseis tipos de tarefas referentes ao estudo de números binários foram identificados, conjuntamente, em diretrizes curriculares de Ontario (2008, 2009) e CSTA (2011):
- Ti1: converter um número representado no sistema de numeração binário em um número representado no sistema de numeração decimal;
- Ti2: converter um número representado no sistema de numeração decimal em um número representado no sistema de numeração binário;
- Ti3: representar dados por meio de dígitos binários;
- Ti4: descrever como é realizado o processamento de dados de um computador;
- Ti5: representar tabelas verdade a partir de portas lógicas;
- Ti6: representar portas lógicas a partir de tabelas verdade;
- Ti7: representar expressões booleanas a partir de portas lógicas;
- Ti8: representar portas lógicas a partir de expressões booleanas;
- Ti9: representar números inteiros por meio de dígitos binários;
- Ti10: representar números racionais por meio de dígitos binários;
- Ti11: converter um número representado no sistema de numeração hexadecimal em um número representado no sistema de numeração binário;
- Ti12: converter um número representado no sistema de numeração binário em um número representado no sistema de numeração hexadecimal;
- Ti13: relacionar expressões booleanas às portas lógicas por meio de representações de símbolos, de números e de expressões;
- T14: mostrar como uma sequência de bits pode ser utilizada para representar dados (alfanuméricos);
- Ti15: explicar os princípios de segurança a partir de codificação binária; àTi16: comprimir textos e imagens.
As duas técnicas que identificamos em diretrizes curriculares internacionais de Computação não são exemplificadas; são técnicas para executar o tipo de tarefa Ti3: mecanismos para representar dados. A técnica 1 – o jogo de “cadeiras binárias” – identificada em Ontario (2008), recorre a associação de dígitos binários, 1 ou 0, ao estado do estudante está em pé ou sentado. A outra técnica, técnica 2, foi identificada em CSTA (2011). Ela recorre à associação de dígitos binários, 1 ou 0, ao estado da imagem conter pixels com cores pretas ou não.
As diretrizes curriculares internacionais de Matemática (ONTARIO, 2005, 2007) assim como as nacionais não sugerem o sistema de numeração binário como conteúdo básico de ensino escolar. Porém, as diretrizes curriculares nacionais de Matemática abordam as unidades de medida da informática: bytes, quilobytes, megabytes, etc. Elas apenas apresentam tipos de tarefas e nenhuma técnica, tecnologia e teoria.
Concluímos também que as diretrizes curriculares oficiais nacionais de Matemática configuram-se como uma praxeologia pontual. Apresentam quatro tipos de tarefas referentes ao estudo de números binários a ser estudado, a partir dos anos finais do Ensino Fundamental:
- Tn1: reconhecer a capacidade de memória do computador como uma grandeza;
- Tn2: identificar unidades de medidas da informática, como: bytes, quilobytes, megabyte e gigabytes;
- Tn3: usar unidades de medida da informática;
- Tn4: converter unidades de medida da informática.
Portanto, as diretrizes curriculares de Matemática (nacionais e internacionais) não sugerem o sistema de numeração binário como tema básico de estudo em nível de Ensino Fundamental e nem Ensino Médio. Por outro viés, as diretrizes curriculares internacionais de Computação, Ontario (2008, 2009) e CSTA (2011), contemplam os números binários como um dos seus fundamentos básicos, necessários para melhorar a compreensão de saberes da própria Computação (saber intracomputação); são favoráveis à inserção da disciplina Computação na educação escolar porque seus saberes podem auxiliar o entendimento de outras ciências. Especificamente, CSTA (2011) sugere: o ensino de números binários a partir do k-3 (crianças de 8-9 anos de idade): recorrer à sequência de bits para representar a informação alfanumérica; relacionar conteúdos da Matemática e da Computação. Ontario (2009) sugere o ensino de números binários e lógica digital a partir do k-9 (jovens de 14-15 anos de idade).
Concluímos também que os números binários são definidos em diretrizes curriculares de Ontario (2008, 2009) como tema ou setor de estudo da “disciplina Computação” e não da disciplina Matemática (ONTARIO, 2005, 2007). Resultado diferente do apresentado por Mendes (2018) em relação à análise praxeológica Matemática e Computação de livros didáticos nacionais: o objeto de saber, números binários, constitui como tema de estudo tanto da Computação como também da Matemática.
REFERÊNCIAS BIBLIOGRÁFICAS
Bell, Tim. Computer Science Unplugged: ensinando Computação sem o uso do computador. (L. P. Barreto, Trad.) csunplugged.org, 2011.
BRASIL. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: introdução aos parâmetros curriculares nacionais. Brasília: MEC/SEF, 1997.
______. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Matemática – terceiro e quarto ciclo do ensino fundamental. Brasília: MEC/SEF, 1998.
______.Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Ciências da Natureza, Matemática e suas Tecnologias. Brasília: MEC, 2000.
CEI– Commission Electrotechnique Internationale. Norme Internacionale - 60027-2: 2005, 3ª edição, 2005.
Chevallard, Y. Analyse des pratiques enseignates et didactique des mathematiques: lápproche antropologique, 1998a. Acesso em 11 de abril de 2014, disponível em http://yves.chevallard.free.fr.
CHEVALLARD, Yves. La transposición didáctica: del saber sábio al saber enseñado. Ed Aique, 1998b. Disponível em: < http://www.uruguayeduca.edu.uy/Userfiles/P0001%5CFile%5Cchevallard.pdf > Acesso em janeiro 2014.
Chevallard, Y. Steps towards a new epistemology in Mathematics Education In: 4º Congrés de la European Society for research in mathematics education (CERME France), 2005. Acesso em 5 de novembro de 2014, disponível em http://yves.chevallard.free.fr
Chevallard, Y. Anthropolical approaches in mathematics education. Encyclopedia of Matematics Education, p. Article: 313188, 2013.
CSTA. Computer Science Teachers Association. CSTA k-12 Computer ScienceStandards. New Yor, 2011.
GLASER, A. History of Binary and other nondecimal numeration. [S.l.]: Tomash Publishers, 1981.
Mendes, H. L. Os números binários nas instituições transpositivas: o caso das diretrizes curriculares. XVIII EBRAPEM, 2014
Mendes, H. L. Análise praxeológica de livro didático de Matemática referente ao estudo de números binários. REVEMAT, 10(1), 2015. pp. 199-219.
Mendes, H. L. Análise praxeológica de livro didático de Computação referente ao estudo de números binários. Revista Brasileira de Ensino de Ciências e Tecnologia, 9(3), 2016a. pp. 311-333.
MENDES, H. D. L. Transposição didática: o caso das unidades de memória da informática. REVEMAT, 11, n. 2, 2016b. 156-172.
Mendes, H. L. Como medir informação? Revista da Rede Amazônica de Educação em Ciências e Matemática (REAMEC). 5, n.2, 2017a.
MENDES, H. D. L. Análise praxeológica de livros didáticos de matemática: o caso dos números binários. Educação Matemática Pesquisa, São Paulo, 19, n. 1, 2017b. 423-444.
Mendes, H. L. Números binários em livros didáticos de matemática e de computação: uma comparação. Revista Brasileira de Ensino de Ciências e Tecnologia, 2018.
MERTENSEN, Marianne. Praxeology as a tool for the analysis of a science museum exhibit. pp. 217-224. In Bosch, M. et al (Eds.) Um panorama de la TAD. Centre de Recerca Matemática, Campus de Bella-Terra Barcelona, 2011. ISSN: 2014-2323. Eletrônica: 2014-2331. III Congreso Internacional sobre la TAD (Sant Hilari Sacalm, 25-29 enero 2010).
ONAGA, Dulce Satiko; MORI,Iracema. Matemática: ideias_e_desafios. 9º ano. 17 ed: Saraiva Livreiros Editores, 2012.
Ontario. Mathematics Curriculum (grades 9 and 10), 2005. Acesso em 14 de abril de 2013, disponível em http://www.edu.gov.on.ca/eng/curriculum/secondary/math.html
______. Mathematics Curriculum (grade 11 and 12), 2007. Acesso em 14 de abril de 2013, disponível em http://www.edu.gov.on.ca/eng/curriculum/secondary/math.html
______. The Otario Curriculum (grades 10 to 12): Cumputer Studier. 2008. Acesso em 14 de abril de 2013, disponível em http://www.edu.gov.on.ca/eng/curriculum/secondary/computer10to12_2008.pdf
______. The Ontario Curriculum (grades 11 and 12): Technological Education , 2009. Acesso em 14 de abril de 2013, disponível em http://www.edu.gov.on.ca/eng/curriculum/secondary/teched910curr09.pdf
______. Kindergaten to grade 12: policy and program requeriments, 2011. Acesso em 14 de abril de 2013, disponível em http://www.edu.gov.on.ca/eng/document/policy/os/index.html
Pernambuco. Parâmetros curriculares de Matemática para o ensino fundamental e médio: Recife, 2012.
SBC. Sociedade Brasileira de Computação: Currículo de referências da SBC para cursos de graduação em Computação e informática, 1999.
SI: Sistema Internacional de Unidades. Traduzido de: Le Système international d’Unités: Duque de Caxias, RJ: INMETRO/CICMA/SEPIN, 2012.
SOUZA, Joamir; PATARO, Patricia Moreno. Vontade de saber Matemática. 7º ano. São Paulo: FTD, 2012.
TRIGUEIROS, María; GASCÓN, Josep; BOSCH, Marianna. Tres modalidades de diálogo entre APÓS y TAD In Bosch, M et al. Un panorama de la TAD (pp. 77-116) III Congreso Internacional sobre la TAD (Sant Hilari Sacalm, 25-29 enero 2010) Conferencias
UNESCO. Informática para a educação básica: um currículo para as escolas/por um grupo de trabalho da IFIP coordenado por Tom and Weert. (L. Aristides, Trad.) Brasília: MEC/UNB, 1997.
Notas
Autor notes
Ligação alternative
https://periodicoscientificos.ufmt.br/ojs/index.php/reamec/article/view/7226 (pdf)

