



CONTRIBUIÇÕES DO SOFTWARE GEOGEBRA NAS AULAS COM SÓLIDOS GEOMÉTRICOS DE FACES PLANAS NOS ANOS INICIAIS DO ENSINO FUNDAMENTAL
CONTRIBUTIONS OF THE GEOGEBRA SOFTWARE IN LESSONS WITH FLAT FACES GEOMETRIC SOLIDS IN THE FIRST YEARS OF FUNDAMENTAL EDUCATION
REAMEC – Rede Amazônica de Educação em Ciências e Matemática
Universidade Federal de Mato Grosso, Brasil
ISSN-e: 2318-6674
Periodicidade: Frecuencia continua
vol. 8, núm. 3, 2020
Recepção: 16 Julho 2020
Aprovação: 12 Setembro 2020
Resumo: Este artigo apresenta resultados parciais de uma pesquisa de mestrado concluída em 2020, que buscou resposta para a seguinte questão de pesquisa: De que forma o software GeoGebra potencializa o processo de ensino de sólidos geométricos com faces planas nos anos iniciais do Ensino Fundamental? Nesta perspectiva, definimos como objetivo investigar as contribuições do software GeoGebra quando utilizado por alunos do 4º ano do Ensino Fundamental para a realização de uma atividade de sólidos geométricos com faces planas. Trata-se de uma pesquisa de cunho qualitativo, com abordagem da Engenharia Didática, cujos resultados apresentados contribuíram para evidenciar as potencialidades que o uso do GeoGebra representa para o desenvolvimento de aulas mais dinâmicas. Desse modo, os dados analisados possibilitaram identificar resultados positivos em relação ao ensino sobre os sólidos geométricos com faces planas, haja vista que a dinamicidade e as potencialidades oferecidas pelo GeoGebra contribuíram para os processos de ensino e de aprendizagem da Geometria Espacial com alunos dos anos iniciais do Ensino Fundamental. Isso, porque, os alunos puderam construir conceitos a partir da visualização e manipulação das figuras na tela do computador, uma vez que as potencialidades do GeoGebra contribuíram para os alunos estabelecerem conexões entre a construção das figuras e a compreensão das propriedades dessas figuras.
Palavras-chave: Anos Iniciais do Ensino Fundamental, Sequência Didática, Tecnologia Digital.
Abstract: This article presents partial results of a master's research completed in 2020, which sought an answer to the following research question: How does the GeoGebra software enhance the process of teaching geometric solids with flat faces in the early years of elementary school? In this perspective, we defined as an objective to investigate the contributions of the GeoGebra software when used by students of the 4th year of Elementary School to carry out an activity of geometric solids with flat faces. It is a qualitative research, with a Didactic Engineering approach, whose results have contributed to highlight the potential that the use of GeoGebra represents for the development of more dynamic classes. In this way, the analyzed data made it possible to identify positive results in relation to teaching about geometric solids with flat faces, given that the dynamics and the potential offered by GeoGebra contributed to the teaching and learning processes of Spatial Geometry with students of the early years Elementary School. This is because the students were able to build concepts from the visualization and manipulation of the figures on the computer screen, since the potential of GeoGebra contributed for the students to establish connections between the construction of the figures and the understanding of the properties of these figures.
Keywords: Early Years of Elementary School, Following teaching, Digital Technology.
1 INTRODUÇÃO
A sociedade contemporânea vem sofrendo profundas transformações, decorrentes a partir da eclosão das tecnologias digitais (TD). Com isso, os alunos buscam por aulas mais atrativas que supram suas necessidades como estudante, uma vez que, segundo Prensky (2001), esses alunos são considerados “Nativos Digitais”. Diante disso, faz-se necessário mudanças na forma de ensinar, buscando estratégias de ensino eficazes que atendam esse público nascido na “Era Digital”.
Nesse viés, este artigo apresenta parte da aplicação de uma Sequência Didática (SD), cujo objetivo foi ensinar conceitos de Sólidos Geométricos com faces planas por meio do software GeoGebra para alunos do 4º ano do Ensino Fundamental. Entendemos a relevância desta investigação pois, pesquisas desta natureza nos anos finais do Ensino Fundamental e no Ensino Médio ocorrem com frequência. Entretanto, o mesmo não ocorre nos anos iniciais do Ensino Fundamental.
Além disso, a consolidação pela escolha dessa investigação se deu pois, a primeira autora, como professora pedagoga, que ensina matemática, e que busca diferentes metodologias e recursos de aprendizagens, acreditou que poderia desenvolver um produto que viesse auxiliar professores que também não são formados em matemática, mas que ensinam matemática nos anos iniciais do Ensino Fundamental. Com isso, contribuiria para que esses docentes possam, também, utilizar o software GeoGebra como recurso didático tecnológico nas aulas de matemática e, assim, criar possibilidades de aulas mais dinâmicas e atrativas para os alunos.
Como parte dessa investigação, identificamos algumas pesquisas desenvolvidas com essa vertente e que aqui destacamos pois, contribuíram para a realização dessa pesquisa, ainda em andamento. Assim, salientamos que as pesquisas de Pereira (2015), Nascimento (2012), Ganeto et al (2018) e Souza et al (2017) evidenciam que o software GeoGebra e a dinamicidade que esse recurso apresenta pode favorecer de forma mais autônoma a aprendizagem dos alunos, além de melhorar e/ou modificar a metodologia aplicada pelo professor.
Os resultados das pesquisas mostram pontos positivos no sentido de que pesquisas no âmbito da Geometria Espacial e o software GeoGebra nos anos iniciais são necessárias, visto que é essencial trabalhar com recursos tecnológicos nos dias atuais. D’Ambrosio (1986) chama atenção para o fato de que, em muitas situações, o aluno se mostra mais confortável com o uso de tecnologias, como o computador e softwares, do que o próprio professor. Isso, porque, nos últimos tempos, as crianças e jovens fazem uso dessa tecnologia em jogos e brincadeiras que são dispostos a eles por meio da tecnologia.
Para tanto, as pesquisas encontradas apontam a necessidade de mais investigação nos anos iniciais, pois o GeoGebra foi pensado para todos os níveis de ensino, inclusive para os anos iniciais. Mas, a maioria das pesquisas mostram que a aplicabilidade deste recurso se concentra nos anos finais do Ensino Fundamental, Ensino Médio e Ensino Superior. E também, nos cursos de formação continuada de professores de matemática.
Autores como Perez (1991) e Pavanello (1993), apontam que as dificuldades de ensinar, muitas vezes, passam pela relação do professor e o saber matemático e também da sua experiência profissional. A primeira problemática que se percebe é que professores do Ensino Fundamental não possuem conhecimento necessários de Geometria para fazer a transposição didática na sua prática de sala de aula. A segunda razão é a falta de material e recursos didáticos eficientes. Esses apontamentos contribuem tanto para o fracasso da Geometria como também, para o desempenho dos alunos, anos após anos de estudos.
Nesse contexto, constituímos uma investigação buscando respostas para a seguinte questão: De que forma o software GeoGebra potencializa o processo de ensino de sólidos geométricos com faces planas nos anos iniciais do Ensino Fundamental?
Buscando respostas à referida questão de pesquisa, consideramos que o software GeoGebra foi idealizado como estratégia de ensino da Geometria, Álgebra, Cálculo e Estatística, permitindo a professores e alunos possibilidades de explorar, conjecturar, investigar tais conteúdos na construção do conhecimento matemático (INSTITUTO GEOGEBRA, 2020). Então, delineamos como objetivo, investigar as contribuições do software GeoGebra, quando utilizado por alunos do 4º ano do Ensino Fundamental na realização de atividades de sólidos geométricos com faces planas. Com isso, procuramos ampliar as pesquisas voltadas para alunos dos anos iniciais do Ensino Fundamental, a fim de fortalecer o processo de ensino e consequentemente, a aprendizagem com alunos dessa etapa de ensino.
2 REFERENCIAL TEÓRICO
Na sequência são apresentadas reflexões teóricas e introdutórias acerca das contribuições das TD na Educação Matemática e, também, sobre a Geometria Espacial nos anos iniciais, buscando apresentar elementos necessários para a análise da pesquisa realizada.
2.1 Contribuições das Tecnologias Digitais na Educação Matemática
As transformações ocorridas com a inserção das TD exigem novas competências para analisar as novas formas de comunicar, de pensar, ensinar e aprender. Desta forma, o modelo tradicional de ensino perde espaço com a implementação das TD como aporte didático tecnológico que contribui para o desenvolvimento dos processos de ensino e de aprendizagem. Neste sentido, Kenski (1998, p. 60) argumenta que “as velozes transformações tecnológicas da atualidade impõem novos ritmos e dimensões à tarefa de ensinar e aprender. É preciso que se esteja em permanente estado de aprendizagem e de adaptação ao novo”. Nesta perspectiva, é premente que sejam abandonadas as práticas do ensino estático e sigamos para uma aprendizagem que tenha significado para os alunos. Nesse contexto, é fundamental que o professor se torne mediador e orientador na aprendizagem promovida por meio de tecnologias digitais, pois é seu papel criar novas possibilidades para ensinar e aprender.
Assim, é preciso buscar o desenvolvimento de práticas que favoreçam o raciocínio lógico, a autonomia e a criatividade na resolução de problemas contextualizados com as TD. Para isso, é importante compreendermos que,
[...] a variedade de recursos que temos à nossa disposição permite o avanço na discussão que trata de inserir a escola na cultura do virtual. A tecnologia digital coloca à nossa disposição ferramentas interativas que incorporam sistemas dinâmicos de representação na forma de objetos concreto abstratos. São concretos porque existem na tela do computador e podem ser manipulados e são abstratos porque respondem às nossas elaborações e construções mentais (GRAVINA; BASSO, 2012, p. 14).
Dando força a essa ideia, Celani (2004) afirma que, para ajustar a escola ao ritmo da modernidade, é necessário que a cultura da certeza dê lugar à cultura da incerteza. Afinal, a disposição para a mudança, para abandonar os “velhos mapas” depende de fatores que envolvem professores e alunos na busca incessante por conhecimentos.
Nesse sentido, a prática educativa se modifica quando o professor abre possibilidades de ensinar por meio das TD. Com isso, este permite que seus alunos interajam com diferentes meios para busca de informações. Esta proposta é ressaltada por Brunner (2004, p. 25), quando afirma que “o problema para a educação na atualidade não é onde encontrar a informação, mas como oferecer acesso a ela sem exclusões e, ao mesmo tempo, aprender e ensinar a selecioná-la, avaliá-la, interpretá-la, classificá-la e usá-la”. É neste sentido que o professor precisa estar preparado para lidar com a avalanche de informações trazidas pelos alunos inseridos no contexto digital. Assim, o papel do educador é essencial para traçar estratégias de ensino com TD na escola.
Ainda, Santana e Medeiros (2014, p. 7) destacam que o papel do professor é fazer com que o aluno consolide seu conhecimento, pois “o papel de mediador é fundamental para criar situações nas quais o aluno é levado a refletir”. Assim, os professores transformam suas práticas quando aprendem a refletir acerca do uso das TD e orientam seus alunos de forma crítica, de modo que não sejam manipulados por elas. Para consolidar esta ideia, Gadotti (2011, p. 25) afirma que o professor “deixará de ser um lecionador para ser um organizador do conhecimento, um mediador do conhecimento, um aprendiz permanente, um construtor de sentidos, um cooperador e, sobretudo, um organizador de aprendizagem”.
Por isso, o docente passa a refletir sobre o conceito de TD e informação versus sala de aula. Neste processo ele passa a ser o orientador no processo de intermediar e/ou mediar as aprendizagens dos alunos para utilização dos recursos digitais de forma eficaz. Isto porque, não adianta apenas obter as informações com as TD, mas conhecer e saber tirar proveito dos recursos disponíveis e transformá-los em conhecimento (BORBA; VILLARREAL, 2005).
É neste contexto que o GeoGebra se destaca, dentre as muitas possibilidades de TD a serem utilizadas por professores e alunos. Isso, pois, esse software, “[...] ao longo dos anos, [...] foi consolidando seu status enquanto uma tecnologia inovadora na educação matemática” (BORBA; SILVA; GADANIDIS, 2018, p. 50).
O GeoGebra foi criado em 2001, como tese do austríaco Markus Hohenwarter da Universidade de Salzburgo, sendo considerado uma ferramenta dinâmica e interativa para o ensino de Álgebra e Geometria (INSTITUTO GEOGEBRA, 2020). Os recursos tecnológicos disponíveis nesse software podem colaborar com o processo de ensino da matemática, pois, podem possibilitar aos alunos desenvolver atividades que permitem a investigação, a interação e a testagem, facilitando o processo de construção do conhecimento. Assim, o aluno participa da elaboração da resolução interagindo assim com o software, sejam com atividades algébricas ou geométricas (MORAIS, 2012).
Então, considerando essas potencialidades do GeoGebra, entendemos que esse software pode contribuir com os processos de ensino e de aprendizagem de Geometria Espacial, inclusive, com alunos dos anos iniciais, como ocorreu em nossa pesquisa.
2.2 Geometria Espacial nos anos iniciais do Ensino Fundamental
para abordar o ensino da geometria, entendemos ser importante descrever um breve histórico do seu surgimento. Isso, porque, ela faz parte do cotidiano da humanidade desde os primórdios, sendo um dos ramos mais antigos da matemática que estuda o espaço e as formas.
Documentos escritos pelos egípcios, por exemplo, deixaram uma grande quantidade de informações sobre a Geometria. Além dos documentos, a construção das pirâmides e de outros monumentos da civilização egípcia revelam o uso de conhecimentos geométricos. Os primeiros registros apontam sua origem a partir da necessidade constante de medir e organizar a terra para o plantio. O que nos leva a crer que essa forma de organização dá origem a palavra Geometria, já que o termo “geometria” é de origem grega, em que geo provém de gaia/terra e metria de métron/medida.
É provável que a civilização egípcia tenha desenvolvido a Geometria, pois, por um lado, as inundações anuais do delta do Nilo traziam nutrientes aos campos de cultivo, tornando a terra mais fértil, por outro, desfaziam as marcas físicas que delimitavam as terras, provocando conflitos entre os proprietários.
Assim, para Boyer (2003), Heródoto[3] acreditava que a Geometria surgiu em virtude da necessidade prática de medir as terras, e Aristóteles[4] entendia que a Geometria surgiu como prática de lazer entre os sacerdotes egípcios que se dedicavam aos estudos geométricos. No entendimento desses dois filósofos, percebe-se pensamentos distintos sobre o surgimento da Geometria, pois um acreditava nas necessidades de mensuração da terra pós enchentes no Nilo e o outro no entretenimento da classe sacerdotal no Egito. Segundo Boyer (2003, p. 6), Heródoto escreveu,
O rei Sesóstris [...] repartiu o solo do Egito entre seus habitantes [...] Se o rio levava qualquer parte do lote de um homem... O rei mandava pessoas para examinar, e determinar por medida a extensão exata da perda... Por esse costume, eu creio, é que a Geometria veio a ser conhecida no Egito, de onde passou para a Grécia.
Fontes documentais, como os papiros encontrados por volta de 1650, possibilitam verificar que os egípcios conseguiram notáveis realizações referente ao cálculo de volumes, o que indica que já usavam noções de Geometria Espacial. Para muitos historiadores, o mais notável feito da geometria métrica egípcia é a regra correta para o cálculo de volume das pirâmides de base quadrada, encontrada no papiro Moscou. Apesar de tantas realizações notáveis no Egito, somente graças aos gregos é que a Geometria, especialmente a espacial, se livrou da ênfase dada à mensuração e de seus vínculos aritméticos, ou seja, aos cálculos.
Indo além dessa perspectiva histórica, buscamos o significado da palavra geometria. Segundo o dicionário online de português (Dicio), Geometria é “A parte da matemática que estuda rigorosamente o espaço e as formas (figuras e corpos) que nele podem estar” (GEOMETRIA, 2019). Ela é a área da matemática que se dedica a questões relacionadas com forma, tamanho, posição relativa entre figuras ou propriedades do espaço. Ainda,
a Geometria é descrita como um corpo de conhecimentos fundamental para a compreensão do mundo e participação ativa do homem na sociedade, pois facilita a resolução de problemas de diversas áreas do conhecimento e desenvolve o raciocínio visual. Está presente no dia a dia como nas embalagens dos produtos, na arquitetura das casas e edifícios, na planta de terrenos, no artesanato e na tecelagem, nos campos de futebol e quadras de esportes, nas coreografias das danças e até na grafia das letras. Em inúmeras ocasiões, precisamos observar o espaço tridimensional como, por exemplo, na localização e na trajetória de objetos e na melhor ocupação de espaços (FORSTER, 2012, p. 10).
Ou seja, a Geometria está presente no nosso dia a dia. Desta forma, faz-se necessário estudá-la, entendê-la, compreendê-la observando o espaço bidimensional e tridimensional em que vivemos. Assim, Lorenzato (2006) destaca a importância da Geometria, que tem função essencial na formação dos indivíduos, pois ela possibilita uma interpretação mais completa do mundo, uma comunicação mais abrangente de ideias e uma visão equilibrada da matemática. Além disso, dependendo de como são trabalhados os conceitos geométricos, surgem possibilidades para o aluno explorar, representar, construir, investigar, perceber, discutir, descobrir e descrever propriedades, tudo isso é fundamental no processo de ensino da matemática.
Embora existam muitas geometrias, aquela que é abordada no Ensino Fundamental e Médio é a euclidiana, que “estuda as propriedades das figuras e dos corpos geométricos enquanto relações internas entre os seus elementos, sem levar em consideração o espaço” (NACARATO; PASSOS, 2003, p. 24), e que recebe esse nome em homenagem a Euclides, pois sua obra “Elementos” já foi impressa em mais de mil edições desde a primeira delas em 1482 e por mais de dois milênios esse trabalho dominou o ensino de Geometria (EVES, 2004, p. 168).
A importância do ensino e aprendizagem da Geometria nos anos iniciais do Ensino Fundamental está fundamentada nos documentos que regem a da Educação Básica. Como exemplo, citamos os PCN (BRASIL, 1998, p. 39), que destacam a importância desse ramo da matemática, que também serve de instrumento para outras áreas do conhecimento:
O aluno desenvolve um tipo especial de pensamento que lhe permite compreender, descrever e representar, de forma organizada, o mundo em que vive. [...] O trabalho com noções geométricas contribui para a aprendizagem de números e medidas, pois estimula a criança a observar, perceber semelhanças e diferenças, identificar regularidades e vice-versa.
A Geometria está estritamente relacionada com o espaço em que vivemos, pois se faz presente nas construções humanas realizadas, inclusive, a milhares de anos. Assim, seu estudo é primordial, também nos anos iniciais. Nesse viés, e em conformidade com Lorenzato, (1995, p. 5)
para justificar a necessidade de se ter a Geometria na escola, bastaria o argumento de que sem estudar Geometria as pessoas não desenvolvem o pensar geométrico ou o raciocínio visual e, sem essa habilidade, elas dificilmente conseguirão resolver as situações de vida que forem geometrizadas; também não poderão se utilizar da Geometria como fator altamente facilitador para a compreensão e resolução de questões de outras áreas de conhecimento humano. Sem conhecer Geometria a leitura interpretativa do mundo torna-se incompleta, a comunicação das ideias fica reduzida e a visão da Matemática torna-se distorcida.
Entende-se, assim, que a Geometria é uma aprendizagem necessária ao desenvolvimento dos alunos, pois, situações diversas de aprendizagens necessitam de percepções adquiridas no estudo da Geometria. Percepções estas trazidas na BNCC (BRASIL 2018, p. 269):
A Geometria envolve o estudo de um amplo conjunto de conceitos e procedimentos necessários para resolver problemas do mundo físico e de diferentes áreas do conhecimento. Assim, [...] estudar posição e deslocamentos no espaço, formas e relações entre elementos de figuras planas e espaciais pode desenvolver o pensamento geométrico dos alunos. Esse pensamento é necessário para investigar propriedades, fazer conjecturas e produzir argumentos geométricos convincentes.
Nesse sentido, o estudo da Geometria é essencial para desenvolver no indivíduo o pensamento geométrico, fundamental para entender e resolver problemas nas outras áreas do conhecimento. Particularmente nos anos iniciais, com o estudo da Geometria, espera-se que,
Os alunos identifiquem e estabeleçam pontos de referência para a localização e o deslocamento de objetos, construam representações de espaços conhecidos e estimem distâncias, usando, como suporte, mapas (em papel, computadores, tablets ou smartphones), croquis e outras representações. Em relação às formas, espera-se que os alunos indiquem características das formas geométricas tridimensionais e bidimensionais, associem figuras espaciais a suas planificações e vice-versa. [...] O estudo das simetrias deve ser iniciado por meio da manipulação de representações de figuras geométricas planas em quadriculados ou no plano cartesiano, e com recurso de softwares de geometria dinâmica (BRASIL 2018, p. 270 – grifo nosso).
Neste aspecto, o ensino de Geometria ganha reforço quando surgem possibilidades de ensiná-la com o uso das TD, como os softwares relacionados à geometria dinâmica. Assim, os alunos, por meio da visualização e a manipulação de objetos na tela do computador, podem conjecturar as variedades de construções, as quais consequentemente não conseguiriam apenas utilizando o modo estático, ou seja, lápis e papel. A dinamicidade possibilitada pelos softwares de geometria dinâmica abre inúmeras possibilidades de interação com as construções, proporcionando um ensino mais real e próximo da vivência dos alunos.
Lorenzato (2006) enfatiza que a criança realiza suas primeiras experiências de vida quando vê, ouve e manuseia com a ajuda da linguagem, mas principalmente com o auxílio da percepção espacial iniciando suas descobertas. Isso é confirmado também por Abrantes et al (1999, p. 71), quando diz:
As primeiras experiências das crianças são geométricas e espaciais, ao tentarem compreender o mundo que as rodeia, ao distinguirem em um objeto do outro. [...]. Aprendendo a movimentar-se de um lugar para o outro, estão a usar ideias espaciais e geométricas para resolver problemas. Esta relação com a Geometria prossegue ao longo da vida.
Nesse ínterim, é importante ressaltar que a criança deve ser incentivada a explorar o espaço em que vive, pois a efetiva aprendizagem acontece “pelas ações mentais que a criança realiza quando compara, distingue, separa e monta” (LORENZATO, 2006, p. 44). São essas habilidades que podem estimular sua percepção visual e permitir que ela se localize no espaço à sua volta.
Dessa forma, a Geometria pode apresentar-se para a criança de forma prática. Neste sentido, ela constrói suas primeiras noções espaciais por meio dos sentidos e dos movimentos. Essa construção ocorre de forma progressiva e tem como início a percepção do próprio corpo, a presença no mundo e o seu redor. Somente após esse momento, a criança atinge a compreensão do espaço representado em desenhos, mapas, etc.
Portanto, o pensamento geométrico desenvolve-se inicialmente pela visualização: a criança é capaz de identificar uma figura por sua forma, aparência física e por sua imagem. A partir daí, têm início as representações mentais que lhe permitirão trazer à memória objetos e espaços ausentes.
Nesse viés, observamos que a Geometria Espacial está presente no nosso cotidiano. Basta observarmos os objetos, as formas e as construções que nos cercam. Ao realizar essa ação, conseguimos visualizar o volume total, em vez de somente a superfície, ou seja, observamos tudo em três dimensões, ou como é mais conhecido, em 3D e não em 2D. Assim, a Geometria Espacial estuda as figuras geométricas no espaço. Consoante a isso, os PCN (BRASIL, 1998, p. 127) apontam que
[...] O pensamento geométrico desenvolve-se inicialmente pela visualização: as crianças conhecem o espaço como algo que existe ao redor delas. As figuras geométricas são reconhecidas por suas formas, por sua aparência física, em sua totalidade, e não por suas partes ou propriedades.
Nesta perspectiva, é importante que a criança aprenda noção de Geometria e/ou pensamento geométrico observando o espaço onde está inserida e, que venha desenvolver habilidades de resolução de problemas ligados à sua vivência, tanto no contexto escolar como social.
A partir disso, optamos em trabalhar com a Geometria Espacial com o objetivo de despertar a curiosidade e a percepção dos estudantes quanto às figuras geométricas cotidianas que os cercam. Isso, para que eles consigam resolver problemas ligados à sua realidade e, também, porque a Base Nacional Comum Curricular (BNCC) sugere o ensino de Geometria utilizando softwares de geometria dinâmica (BRASIL, 2018).
Nesse viés, Bressan, Bogisic e Grego (2010) apontam que o ensino de Geometria na Educação Básica serve para que o aluno possa interpretar e analisar o mundo físico, atuando em torno dele para então, expressar e interpretar imagens e conceitos, próprios da Matemática ou até mesmo de outras ciências. Em particular, nos anos iniciais do Ensino Fundamental, Tortora e Pirola (2016, p. 106) enfatizam a relevância da aprendizagem da geometria, pois, “[...] possibilita aos sujeitos o desenvolvimento de uma série de habilidades, como orientação espacial, percepção geométrica, abstração, representação mental de imagens, entre outras [...].
Portanto, a Geometria configura-se como uma eficiente conexão que a matemática possui com os outros campos do conhecimento, pois ela se interliga com artes, ciências, história, e, em especial, com a Aritmética e com a Álgebra porque os objetos e relações dela correspondem aos das outras; assim sendo, conceitos, propriedades e questões aritméticas ou algébricas podem se clarificados pela Geometria.
3 PROCEDIMENTOS METODOLÓGICOS
A pesquisa da qual fizemos um recorte é de natureza qualitativa, cuja produção dos dados, segundo Bogdan e Biklen (1994), ocorre em contexto naturais, de modo que não há a necessidade de se levantar ou comprovar hipóteses ou, ainda, medir variáveis. Ainda, por meio dela, é possível compreender os sujeitos e os fenômenos investigados.
Quanto a isso, Godoy (1995, p. 58 – grifo nosso) pontua que esse tipo de pesquisa envolve
A obtenção de dados descritivos sobre pessoas, lugares e processosinterativos pelo contato direto do pesquisador com a situação estudada, procurando compreenderos fenômenos segundo a perspectiva dos sujeitos, ou seja, dos participantes da situação em estudo.
Nesse sentido, a pesquisa qualitativa se apresenta com o objetivo de interpretar o fenômeno em observação. Ou seja, analisar e compreender os fenômenos investigados. No nosso caso, os fenômenos em investigação são os processos de ensino e aprendizagem dos estudantes, na vivência de sua realidade, buscando entender esses processos.
Para tanto, utilizamos a Engenharia Didática, pois ela tem se constituído como uma metodologia de investigação científica que procura “extrair relações entre pesquisa e ação [...], sobre o sistema baseado em conhecimentos didáticos preestabelecidos” (ARTIGUE, 1996, p. 2). Trata-se de uma concepção que contempla tanto a dimensão teórica como experimental, pois, a Engenharia Didática consegue interligar o plano teórico da racionalidade à experimentação da prática educativa, numa execução que envolve desde o pensar das ideias iniciais até a prática.
A produção dos dados desta pesquisa ocorreu a partir da utilização de uma SD desenvolvida considerando as potencialidades do GeoGebra, que é um software de matemática dinâmica. Essa SD teve como objetivo contribuir para o desenvolvimento da habilidade de “Associar prismas e pirâmides a suas planificações e analisar, nomear e comparar seus atributos, estabelecendo relações entre as representações planas e espaciais” (BRASIL, 2018, p. 290), preconizada na BNCC.
Para tanto, consideramos o GeoGebra como alternativa para ensinar Geometria nos anos iniciais do Ensino Fundamental, inclusive como sendo uma possibilidade para ser utilizada por professores que ensinam matemática e/ou atuam nessa área. Ainda que utilizar o GeoGebra nos anos iniciais não seja uma prática comum, assim como ocorre nos anos finais e no Ensino Médio, vislumbramos essa possibilidade e elaboramos uma Sequência Didática com atividades envolvendo o uso do GeoGebra. Essas atividades foram planejadas de modo a possibilitar que os alunos realizassem manipulações de figuras geométricas no GeoGebra, para que então pudessem identificar as figuras geométricas por meio de suas características e percebessem a semelhanças e diferenças entre elas. E ainda, que construíssem figuras geométricas (sólidos geométricos partes planas) a partir das características observadas. Com isso, espera-se, também, auxiliar os alunos no desenvolvimento da linguagem matemática, por meio da caracterização escrita das figuras geométricas e da identificação de figuras a partir da leitura de suas características.
Imbuídos neste contexto, produzimos os dados da pesquisa por meio da aplicação de uma SD para 26 alunos do 4° ano do Ensino Fundamental de uma escola municipal de Boa Vista – Roraima, em 2019. A aplicação dessa SD ocorreu no Laboratório de informática, em 14 hora/aulas, distribuídas igualmente em sete dias. Os alunos trabalharam em duplas, pois essa forma permitiu maior possibilidade de compartilhamento de ideias e de colaboração mútua entre os participantes.
4 ANÁLISES E RESULTADOS
A análise desse artigo compõe-se por meio de um recorte extraído dos dados produzidos na pesquisa. Com esse recorte apresentamos uma atividade produzida na aula referente a poliedros e não poliedros. Nessa aula, pedimos aos alunos que utilizassem o GeoGebra para realizarem a construção de uma figura poliédrica (pirâmide, cubo ou paralelepípedo), identificando as bases, faces, arestas e vértices, destacando-as em cores diferentes para melhor visualização e, consequentemente, melhor compreensão dos conceitos relacionados aos poliedros. No dia da realização dessa atividade, tínhamos os 26 alunos que realizaram a atividade em duplas.
Abaixo, por meio da figura 1, apresentamos a construção realizada por uma dupla de alunos.
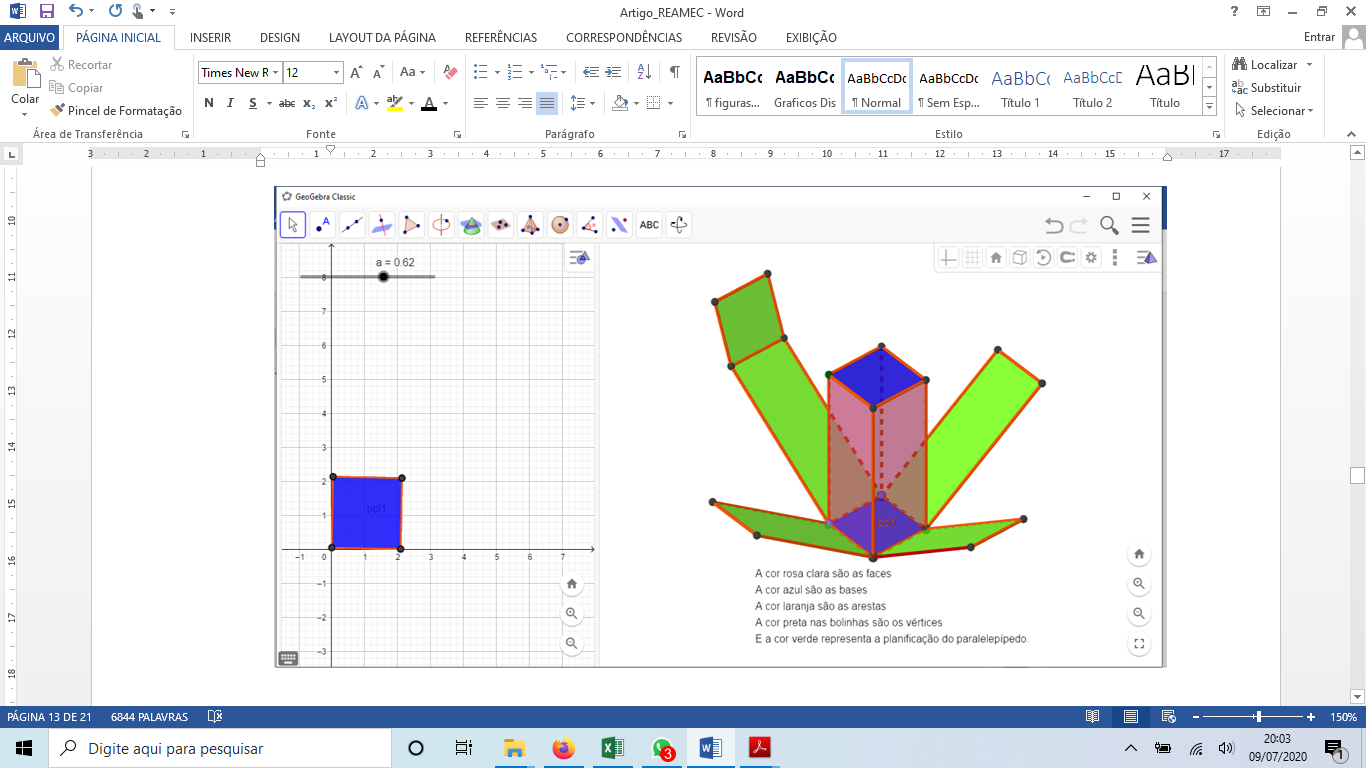
A análise da Figura 1 possibilita observar alguns aspectos que evidenciam que a dupla de alunos conseguiu expressar as características do paralelepípedo: “a cor rosa clara são as faces”; “a cor azul são as bases”; “a cor laranja são as arestas”; “a cor preta nas bolinhas são os vértices” e, “a cor verde representa a planificação do paralelepípedo”. Essa descrição detalhada do paralelepípedo nos leva a acreditar que, a construção realizada no software GeoGebra, assim como a interação desses alunos com o objeto construído, foram fatores determinantes para que esses alunos desenvolvessem conceitos geométricos. Afirmamos isso pois, essa ideia é reforçada, por Abrantes et al (1999, p. 68) quando destacam que,
estas ferramentas computacionais (Cabri-Geomètre,Geometer’s Sketchpad, GeoGebra, etc.) geram uma nova abordagem no ensino e aprendizagem da geometria, pois permitem a construção e manipulação de objetos geométricos e a descoberta de novas propriedades desses objetos, através da investigação das relações ou medidas que se mantêm invariantes.
Assim, observamos que a introdução das TD, aqui representada por meio do GeoGebra, no processo de ensino de alunos de 4º ano, permite um aprendizado dinâmico e concreto, favorecendo o aprofundamento dos conceitos matemáticos relacionados à Geometria Espacial. É importante ressaltar que, com esta atividade os alunos conseguiram superar a dificudade encontrada em outra outra atividade que também envolveu paralelepipedos. Acreditamos que essa superação de dificuldades deu-se em razão da ênfase que foi dada na construção da figura com detalhamento de suas características, possibilitada pelo software GeoGebra. Os resultados positivos que apontamos são apresentados no Gráfico 1, que apresenta o rendimento obtido pelas 13 duplas de alunos que realizaram essa tarefa.
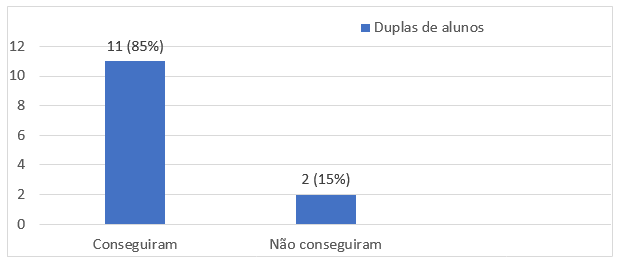
Acreditamos que o resultado positivo apresentado por meio do Gráfico 1 deve-se, essencialmente, às potencialidades que os recursos do GeoGebra oferecem aos alunos. Isso pois, foi por meio da utilização desses recursos, que alunos do 4º ano puderam “manipular” o paralelepípedo, tendo assim, uma interação dinâmica com esse objeto, o que possibilitou, a nosso ver, que os alunos adotassem estratégias para realizar a tarefa com sucesso.
Nesse viés, entendemos que o software GeoGebra traz dinamicidade para essas construções, pois, possibilita inúmeras conjecturas referente às figuras representadas. Desta forma, o pensamento e conceitos geométricos podem ir se desenvolvendo, conforme ocorre a manipulação desses objetos. Afirmamos isso, pois, conforme Zulatto (2002, p. 90), com softwares de geometria dinâmica, “[...] é possível visualizar as figuras em várias posições, em um curto espaço de tempo, devido à possibilidade de arrastá-las pela tela. Assim, é possível visualizar ‘todos’ os casos de uma mesma figura geométrica [...]”.
Ou seja, o envolvimento dos alunos em representar o problema por meio das TD, no caso, o software GeoGebra, evidencia que o computador pode ser uma ferramenta que ajuda aprimorar os conhecimentos nos processos de ensino e aprendizagem. Inclusive, com alunos dos anos iniciais, por proporcionar novas experiências dentro do contexto que está sendo ensinado em sala de aula. Além disso, a utilização de softwares livres nas escolas é uma realidade, contribuindo para a difusão dessas soluções tecnológicas de baixo custo que auxiliam a inclusão das escolas públicas na era da informação.
5 CONSIDERAÇÕES FINAIS
Este artigo apresentou o recorte de uma pesquisa de mestrado recém concluída, cujo objetivo é analisar o uso do software GeoGebra como um recurso potencializador no processo de ensino de Geometria Espacial por meio de resolução de problemas com alunos do 4° ano do Ensino Fundamental. A produção dos dados analisados neste artigo deu-se por meio de uma atividade realizada em uma aula sobre poliedros e não poliedros.
Entendemos que o desenvolvimento dessa atividade, realizada com o software GeoGebra, possibilitou que alunos dos anos iniciais do Ensino Fundamental pudessem ir além dos resultados obtidos com atividades envolvendo o estudo de poliedros e não poliedros, sem os recursos de softwares de geometria dinâmica. Com a realização dessa tarefa no GeoGebra, os alunos puderam construir conceitos a partir da visualização e manipulação das figuras na tela do computador. Assim, entendemos que as potencialidades do GeoGebra contribuem com possibilidades para que os alunos estabeleçam conexões entre a construção das figuras e a compreensão das propriedades dessas figuras. Assim, entendemos que a visualização também favorece a produção de sentidos na aprendizagem matemática (BORBA; SILVA; GADANIDIS, 2018).
Desta forma, a dinamicidade trazida por meio de softwares como o GeoGebra rompe com a visão de construções de conceitos que utilizam o modelo estático, dando lugar à dinamicidade. Por isso, entendemos que o uso do GeoGebra potencializa descobertas antes ocultas pela tecnologia estática do lápis e papel.
REFERÊNCIAS
ABRANTES, P.; SERRAZINA, L.; OLIVEIRA, I. A Matemática na Educação Básica. Lisboa: Ministério da Educação, 1999.
ARTIGUE, M. Engenharia Didáctica. In: BRUN, J. (Org.) Didática das matemáticas. Lisboa: Instituto Piaget. 1996.
BOGDAN, R. C.; BIKLEN, S. K. Investigação qualitativa em educação: uma introdução à teoria e aos métodos. Porto: Porto Editora, 1994.
BORBA, M. C.; SILVA, R. S.; GADANIDIS, G. Fases da tecnologia digitais em Educação Matemática: sala de aula e internet em movimento. Belo Horizonte: Autêntica, 2018.
BORBA, M. C.; VILLARREAL. M. E. Humans-With-Media and the Reorganization of Mathematical Thinking: information and communication Technologies, modeling, experimentation and visualization. v. 39. New York: Springer, 2005.
BOYER, B. História da Matemática. São Paulo. Tradução Elza F. Gomide. 2ª ed. São Paulo. Edgard Blucher, 2003.
BRASIL. Base Nacional Comum Curricular (BNCC). Educação é a Base. Brasília: MEC/CONSED/UNDIME, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/a-base. Acesso em: 23 dez. 2018.
BRASIL. Secretaria de Educação Fundamental. PCN: matemática / Secretaria de Educação Fundamental. Brasília: MEC/SEF, 1998. Disponível em: https://www.cpt.com.br/pcn/pcn-parametros-curriculares-nacionais-documento-completo-atualizado-e-interativo. Acesso em 11 dez. 2018.
BRESSAN, A. M; BOGISIC, B.; GREGO, K. Razones para enseñar geometría en la educación básica. Mirar, construir, decir y pensar... Novidades Educativas. Buenos Aires. 2010.
BRUNNER, J. J. Educação no encontro com as novas tecnologias. In: TEDESCO, J. C. Educação e novas tecnologias: Esperanças ou incertezas?. São Paulo: Cortez, 2004, p. 17 - 75.
CELANI, M. A. A. Culturas de aprendizagem: risco, incerteza e educação. In: MAGALHÃES, M. C. C. (Org.). A formação do professor como um profissional crítico: linguagem e reflexão. Campinas: Mercado de Letras, 2004, p. 37- 56.
D’AMBROSIO, U. Da Realidade à Ação: Reflexões a Educação e Matemática. São Paulo, Summus Editorial, 1986.
EVES, H. Introdução à História da Matemática. Tradução: Hygino H. Domingues. Editora da UNICAMP. Campinas, SP, 2004.
FORSTER, C. Ensino de Geometria Plana com Auxílio do Tangram. In: 3ª Escola de Inverno de Educação Matemática, Santa Maria, 2012. Universidade Federal de Santa Maria (UFSM). Disponível em: http://w3.ufsm.br/ceem/eiemat/Anais/arquivos/RE/RE_Horbach_Ivan.pdf. Acesso em: 3 set. 2018.
GADOTTI, M. Boniteza de um sonho: ensinar-e-aprender com sentido. 2ª ed. São Paulo: Editora e Livraria Instituto Paulo Freire, 2011. Disponível em: https://www.paulofreire.org/download/boniteza_ebook.pdf. Acesso em: 29 nov. 2018.
GANETO, J. P. A.; SOUZA, M. S. C. C.; GONÇALVES, M. J. S.; DUARTE, S. S. S. GeoGebra no Estudo da Geometria no 2º. Ano do 2º. Ciclo do Ensino Básico de Escolaridade. Revista do Instituto GeoGebra de São Paulo, v. 7, n. 2, p. 127-143, 2018. Disponível em: http://revistas.pucsp.br/IGISP/article/view/34876/26496. Acesso em: 20 dez. 2018.
GEOMETRIA. Dicionário online de Português Dicio, 2019. Disponível em: https://www.dicio.com.br/geometria/. Acesso: em 28 fev. 2019.
GODOY, A. S. Introdução à pesquisa qualitativa e suas possibilidades. In: Revista de Administração de Empresas. São Paulo: v.35, n.2, p. 57-63,1995.
GRAVINA, M. A.; BASSO, M. V. A. Mídias digitais na Educação Matemática. In: GRAVINA, M. A.; BÚRIGO, E. Z.; BASSO, M. V. A.; GARCIA, V. C. V. (Orgs). Matemática, Mídias Digitais e Didática: tripé para formação do professor de Matemática. Porto Alegre: Evangraf, 2012. Disponível em: www.ufrgs.br/espmat/livros/livro2-matematica_midiasdigitais_didatica.pdf. Acesso em: 05 mai. 2018.
INSTITUTO GEOGEBRA. Sobre o GeoGebra, 2020. Disponível em: https://www.pucsp.br/geogebrasp/geogebra.html. Acesso em: 20 jun. 2020.
KENSKI, V. M. Novas tecnologias: o redimensionamento do espaço e do tempo e os impactos no trabalho docente. In: Revista Brasileira de Educação. nº 08, p. 58 -71, 1998.
LORENZATO, S. Educação infantil e percepção matemática. Campinas: Autores Associados, 2006.
LORENZATO, S. Porque não ensinar Geometria? Educação Matemática em Revista. v. 3, n. 4, p. 3-13, 1995. Disponível em: http://professoresdematematica.com.br/wa_files/0_20POR_20QUE_20NAO_20ENSINAR_20GEOMETRIA.pdf. Acesso em: 8 dez. 2019.
MORAIS, R. G. Geometria dinâmica como alternativa metodológica para o ensino de geometria: experiência em um curso de Licenciatura em Matemática. Dissertação (Mestrado Profissional em Educação Matemática). Vassouras, RJ: Universidade Severino Sombra, 2012.
NACARATO, A. M.; PASSOS, C. L. B. A geometria nas séries iniciais: uma análise sob a perspectiva da prática pedagógica e da formação de professores. São Carlos: EdUFSCar, 2003.
NASCIMENTO; E. G. A. Avaliação do uso do software geogebra no ensino de geometria: reflexão da prática na escola. In: Conferencia Latinoamericana de GeoGebra, Uruguay 2012. Actas da Conferencia Latinoamericana de GeoGebra, Uruguay, 2012. Disponível em: http://www.geogebra.org.uy/2012/actas/67.pdf. Acesso em: 26 set. 2018.
PAVANELLO, R. M. O abandono da geometria no Brasil: causas e consequências. Zetetiké. Campinas, v.1, n. 1, p. 7-17, mar. 1993. Disponível em: https://periodicos.sbu.unicamp.br/ojs/index.php/zetetike/article/view/8646822/13724. Acesso em 5 dez. 2018.
PEREIRA, L M G. O software GeoGebra como proposta facilitadora do processo de ensino-aprendizagem da geometria plana no ensino fundamental. 2015. 142 f. Dissertação (Mestrado Profissional em Matemática em Rede Nacional) - Universidade Federal de Goiás, Catalão, 2015. Disponível em: http://repositorio.bc.ufg.br/tede/handle/tede/4822. Acesso em: 5 jun. 2018.
PEREZ, G. Pressupostos e reflexões teóricas e metodológicas da pesquisa participante no ensino de geometria para as camadas populares. 1991. 348 f. Tese (Doutorado em Educação) – Faculdade de Educação, Universidade Estadual de Campinas, Campinas, 1991. Disponível em: http://repositorio.unicamp.br/handle/REPOSIP/252275. Acesso em: 6 dez. 2018.
PRENSKY, M. Nativos Digitais, Imigrantes Digitais, MCB University Press, v. 9, n. 5, p.01-06, out. 2001. Disponível em: https://www.marcprensky.com/writing/Prensky%20-%20Digital%20Natives,%20Digital%20Immigrants%20-%20Part1.pdf. Acesso em: 10 nov. 2018.
SANTANA, J. C.; MEDEIROS, Q. A utilização do uso de novas tecnologias no ensino de ciências. IV SENEPT: Belo Horizonte, 2014.
SOUZA, V. A., MOURA, É. M., OLIVEIRA, J. S. F., SOUZA, A. J. A interação entre o trabalho educativo com software de geometria dinâmica e fotografia no ensino e aprendizagem de figuras geométricas. In: Revista Eletrônica de Educação Matemática – REVEMAT. Florianópolis (SC), v.12, n. 1, p. 114-132, 2017. Disponível em: https://periodicos.ufsc.br/index.php/revemat/article/view/1981-1322.2017v12n1p114. Acesso em: 28 abr. 2019.
TORTORA, E.; PIROLA, N. A. Resolução de problemas geométricos: um estudo sobre o desenvolvimento conceitual e os conhecimentos declarativos de figuras planas nos iniciais do ensino fundamental. In: REAMEC - Rede Amazônica de Educação em Ciências e Matemática, [S. l.], v. 4, n. 1, p. 104-125, 2016. DOI: 10.26571/2318-6674.a2016.v4.n1.p104-125.i5320. Disponível em: https://periodicoscientificos.ufmt.br/ojs/index.php/reamec/article/view/5320. Acesso em: 19 set. 2020.
ZULATTO, Rúbia Barcelos Amaral. Professores de matemática que utilizam softwares de geometria dinâmica: suas características e perspectivas. 2002. vi, 119 f. Dissertação (mestrado) - Universidade Estadual Paulista, Instituto de Geociências e Ciências Exatas, Rio Claro, 2002. Disponível em: http://hdl.handle.net/11449/91012. Acesso em 10 jul. 2020.
Notas
Autor notes
Ligação alternative
https://periodicoscientificos.ufmt.br/ojs/index.php/reamec/article/view/10835 (pdf)

