Abstract: Nepalese education is often inclined towards rote memorization and teacher centered instruction and learning processes. In this regard, how can instruction be actively made more effective as a key idea as researchers take this into account when conducting research in this area. This study forms an ethnographic case study of one of the schools that is transforming itself from a traditional book-based teaching and learning approach to a curriculum specific child friendly learning process. As researchers and teacher trainers we have been involved in teacher training programs for numbers of schools in Nepal. What we have observed during the four years of involvement is that the training solely do not make changes in the school system. This program is helping teachers in making instructional activities that allows them to galvanize their work for increased student involvement. This research also indicates how moral behavior can be developed through math trail activities where students do field work in groups for different objectives. Children develop their understanding through day to day activities where the perspective of different contexts, culture and ethnic groups play a vital role. At this point, we started working on excursion-based instruction. The change in instruction forces them to design activities and projects that demand children to work in outside school context with curricular objectives. It ensured opportunities for participating in hands-on activities and experiential learning. Finally, this research supports the assumption that mathematical knowledge, skill and moral behavior can be developed through different cultural project-based instructional activities and cultural artifacts and practices are key to ensure effectiveness of learning.
Keywords: Ethnomathematics, Machchhindranath Chariot, School Mathematics, Cultural Artifacts, Math Trail.
Resumen: La educación nepalí a menudo se inclina hacia en las rutas de memorización y la instrucción centrada en el maestro y los procesos de aprendizaje. En este sentido, ¿cómo se puede hacer que la instrucción sea más efectiva como idea clave ya que los investigadores tienen esto en cuenta al realizar investigaciones en esta área? Este estudio constituye un estudio de caso etnográfico de una de las escuelas que se está transformando de un enfoque tradicional de enseñanza y aprendizaje basado en libros a un proceso de aprendizaje específico para el currículo específico para niños. Como investigadores y formadores de docentes, hemos participado en programas de formación de docentes para numerosas escuelas en Nepal. Lo que hemos observado durante los cuatro años de participación es que la capacitación únicamente no hace cambios en el sistema escolar. Por lo tanto, este programa está ayudando a los maestros a realizar actividades de instrucción que les permitan impulsar su trabajo para una mayor participación de los estudiantes. Esta investigación también indica cómo se puede desarrollar el comportamiento moral a través de actividades de seguimiento matemático donde los estudiantes realizan trabajo de campo en grupos para promover diferentes objetivos. Los niños desarrollan su comprensión a través de actividades cotidianas donde la perspectiva de diferentes contextos, cultura y grupos étnicos juegan un papel vital. En este punto, comenzamos a trabajar en la instrucción basada en excursiones. El cambio en la instrucción los obliga a diseñar actividades y proyectos que exigen que los niños trabajen fuera del contexto escolar con objetivos curriculares. Este proyecto aseguró oportunidades para participar en actividades prácticas y aprendizaje experimental. Finalmente, esta investigación apoya la suposición de que el conocimiento matemático, la habilidad y el comportamiento moral pueden desarrollarse a través de diferentes actividades de instrucción basadas en proyectos culturales y los artefactos y prácticas culturales son clave para garantizar la efectividad del aprendizaje de los estudiantes.
Palabras clave: Etnomatemáticas, Carruajte Machchhindranath, Matemática Escolar, Artefactos Culturales, Sendero de Matemáticas.
Resumo: A educação nepalesa é frequentemente direcionada para a memorização mecânica e para os processos de ensino e aprendizagem centrados no professor. Nesse sentido, a instrução pode se tornar ativamente mais eficaz como uma ideia-chave quando os pesquisadores consideram esses processos ao realizarem pesquisas nessa área. Essa pesquisa é um estudo de caso etnográfico realizado em uma das escolas que está se transformando de uma abordagem tradicional de ensino e aprendizagem baseada em livros para um processo de aprendizagem baseado em um currículo específico favorável para as crianças. Como pesquisadores e formadores de professores, participamos de programas de treinamento de professores para várias escolas no Nepal. O que observamos durante os quatro anos de envolvimento é que apenas o treinamento não propicia mudanças no sistema escolar. Assim, esse programa está auxiliando os professores na elaboração de atividades instrucionais que lhes permitam galvanizar o seu trabalho para aumentar o envolvimento dos alunos. Essa pesquisa também indica como o comportamento moral pode ser desenvolvido por meio de atividades matemáticas nas quais os alunos realizam trabalhos de campo, em grupos, para promoverem diferentes objetivos. As crianças desenvolvem a sua compreensão por meio de atividades cotidianas, nas quais a perspectiva de diferentes contextos, culturas e grupos étnicos desempenha um papel vital. Nesse ponto, começamos a trabalhar com a instrução baseada em excursões. A mudança na instrução conduz os professores a elaborarem atividades e projetos que exijam que as crianças trabalhem fora do contexto escolar com objetivos curriculares. Esse projeto assegurou oportunidades de participação em atividades práticas e aprendizado experimental. Finalmente, essa pesquisa apoia a suposição de que o conhecimento matemático, a habilidade e o comportamento moral podem ser desenvolvidos por meio de atividades instrucionais diferenciadas baseadas em projetos, artefatos e práticas culturais, que são essenciais para garantir a eficácia do aprendizado dos alunos.
Palavras-chave: Etnomatemática, Carruagem Machchhindranath, Matemática Escolar, Artefatos Culturais, Trilhas de Matemática.
International perspectives on Ethnomathematics: from research to practices
Developing mathematical skills and moral behavior through cultural artifacts: a study of math trail activities at Patan Durbar Square in Nepal
Desarrollando de habilidades matemáticas y comportamiento moral a través de artefactos culturales: un estudio de actividades matemáticas experimentales en la plaza Patan Durbar en Nepal
Desenvolvendo habilidades matemáticas e comportamento moral por meio de artefatos culturais: um estudo de atividades matemáticas experimentais na Praça Patan Durbar no Nepal
Received: 24 September 2019
Accepted: 21 October 2019
Published: 04 March 2020

Nepal is the nation of multiplicity and diversity. A small land locked nation filled with 123 languages in between the lowlands and world’s highest peak Mount Everest. People in different geographies have created different scripts and specific cultures. More precisely, the Terai region is mostly filled with the language and culture focused on Tharu, Chaudhary, and Mushahar community groups. The hill region has a culture designed by Brahmins and Chhetris and in the Himalayan regions dominated by the Lama, Gurung community culture and language. Having this richness in diversity within an extremely poor nation, it is often difficult for Nepalis to value this gift of nature. Rather, our education and increased globalization has created negative effect on our self-perception.
Although, education in the Indian sub-continent started through the implementation of the ancient Gurukula system, modern and formal education in Nepal is very young. It was started by the Rana’s to enable communication with the with East India Company who ruled India for about 100 years. As a consequence to Indian Independence, the same colonial education tradition was established in Nepal by Hugh B. Wood in 1953 (PANDEY, BAHADUR & WOOD, 1956) essentially glorifying the value of English education and delimiting the value of our own cultural and language diversity. The English education has had a chronic effect on our own cultures and languages, as a result of which local cultures and languages did not get primary positions in formal education in Nepal.
For example, children started learning about Christmas and forgetting about Machindranath. Celebrating our own cultures and traditions became equated to backwardness. Shrestha (1997) outlines that when development arrived, farmers who owned a number of cows and plots of land became poor and people who learned English and had big houses were called rich. Similarly, the person who speaks English became superior and the local language speakers became inferior to them.
As a result of which the youth have less access to the knowledge about their own cultures and traditions. For example, many of us do not know how people in 15th century built the huge Temple of Krishna. We can only assume that the people of those times might have their own knowledge and skills to build it, but we do not know how. But is not this supply context and valuable knowledge that the younger generation should know? The younger generation learning in school, should at least know the value of their own culture and civilization. As human development is a cultural process (D’AMBROSIO, 2010) and it is one of the fundamental rights that every individual has, which is the right to enjoy their own culture.
Culture is one of the most important resources for the process of teaching and learning of mathematics (ROSA & OREY, 2013). Considering this aspect of cultural education, as researchers, we chose our present location and the school we are working in, as well the Rato Machindranath Chariot Festival as the context for this research project. This festival is one of the oldest festivals being celebrated by the people in Nepal. In this research, we consider the Rato Machindranath chariot as a cultural artifact and make an attempt to involve school students to find scientific, mathematical, and cultural connections associated with it.
Machindranath is a festival that is one of the oldest traditions celebrated in the Kathmandu Valley. Celebrated between mid-June to July (mostly in Baisakh to Jestha of the Nepali Calendar). Machindranath is the rain god in this region. Historically, it is said that the festival started when the sage Gorakhnath[1], went to meditate while taking snakes as his mat for 12 years. The whole Kathmandu Valley then suffered from severe drought and the three kingdoms (Kathmandu, Lalitpur, and Bhaktpur) of the valley united together to find a solution to this problem.
As a result of which they concluded that the problem could only be solved if they could bring Machindranath, which is the Guru of Gorakhnath, to the valley. They believed that Gorakhnath would surely come to pray for Machindranath and to release the snakes, which would provide rain in the valley. Hence, three people were chosen to complete this task: a farmer from Lalitpur, a king from Kathmandu and a priest from Bhaktpur. These three people visited North India and brought Machindranath to the Kathmandu valley. The presence of Machindranath brought the severe drought to an end.
The school that we have chosen is the school that we have been working in this school since 2015 AD. This school is located in the Lalitpur metropolitan area of Kathmandu, on the way to Bugmati from Jawalekhel. The school is a private school with about 400 students. We first did a need analysis for the school because we wanted to know how the school, teachers, students and community used their resources and perspectives towards teaching and learning activities.
We realized that use of local resources and teacher development programs for preparing school-based curriculum would work well. Then, we trained teachers to develop learning experiences based on curricular objectives prescribed by the National Curriculum Framework. The process was very slow because teachers’ pedagogical knowledge and related teaching strategies were not clear that was especially true in the direction towards where they were moving.
The first achievement of our work was to make teachers’ clear about curriculum, textbooks, and pertinent pedagogies. The next step included, making them clear about future directions of the school as we started to include activities prescribed for school and prescribed excursion activities. The school used to have students visiting the field once a year but did not focus on the curriculum. We encouraged the school to precisely follow curricular goals while enhancing students’ individual capacity. As well, we considered how every learners are intelligent in diverse forms as described by Gardner (1983) and started taking students outside the classroom for learning. Very soon the school agreed to include about 4 excursion activities each year. The Rato Machchhindranath Project that we include in this research is one of the projects carried out by the school.
KWL Strategy was developed by Ogle (1986) as a assessment of students prior knowledge on the given topic. It has three basic components: Know, Want, and Learn (RISWANTO, RISNAWATI & LISMAYANTI, 2014). This strategy follows a constructivist paradigm as knowledge construction. It begins with students pre-knowledge about a given topic. The pre-knowledge that students recalls about the topic are listed in the know column. Using the students pre-knowledge about the topic teacher cracks the discussion on what deeper knowledge do students want to know about and jot down to want to know column. Finally, after conducting the pre-designed activity on what students want to know the learned column is filled with student learning examples.
KWL strategy is mostly used to improve the reading of the students (OGLE, 1986). This strategy can be applied across content areas (ASRI, 2014). Taking this in concern we use this strategy in helping students in excursion activities. We use KWL strategy as a research-based learning tool that guides students through textual learning along with a visit to the Machindranath. Students began by brainstorming everything they know about the Machindranath chariot. Figure 1 shows the Machindranath chariot.

Further, some text based or news-based ideas were used to enhance their learning about the Machindranath. This information is recorded in the know column. Then, students along with teachers discuss together on what they want to know and generate the list of questions on what they want to know about Machindranath chariot. These questions are listed in the want to know column. After a visit and interview with the priest about the Machindranath chariot the answers students got, were placed in learned column.
As part of this work, we discussed with the teachers how we could encourage the students to participate in festivals so that a sense of mutual cooperation could be enhanced. While discussing, we came up with ideas how visiting and observing the longest festival in our district[2] might support mathematics instruction.
Scaffolding strategies became one of the most powerful techniques to empower teachers and students in this project. Scaffolding was used here to support instructional development in order to facilitate teaching and learning processes when students were introduced to new contents (VYGOTSKY, 1978) as well it needed to be directly related to the cultural background of the students. Further Vygotsky (1978) states that children’ thoughts and actions evolve from interacting with their sociocultural background. But only visiting the Machindranath is not the only purpose, making the meaningful learning is the key to the visit. Similarly, Dewey (1916) stresses that knowledge is formed when humans actively interact with their environment.
Then, we sat together and listed out cross curricular objectives to make the visit meaningful, we saw how culture takes root in practically all aspects of human living (SÁNCHEZ, 2018). Hence, the content of mathematics, social studies and language were integrated and allowed instructors to enhance the students’ learning. After finalization of the objectives we participated with students and informed them about the project.
Since the festival has been observed for over 1000 years in Lalitpur, it was decided that it was better if we could use students’ prior knowledge about the Rato Machindranath. Hence, we decided to include KWL strategies in our project. The use of KWL became meaningful because participating students came up with what they wanted to know about Machindranath. Hence, the teacher, along with the students, finalized the questionnaire and we are ready to make interviews and visit to the Machindranath.
After the interview and visit, students jotted down the points that they have found through interview and visit to the learned section of KWL chart. And shared the finding with other group members. In addition, the teachers along with the students discussed what others could do to present their learning of Machindranath and decided to prepare a model of the chariot. Although, the chariot was not proportionate to the actual Machindranath, however, it gives the sense of the chariot with its outer features and students shared their findings with other junior students at assembly. The Figure 2 shows how the researchers have designed the process of the research.
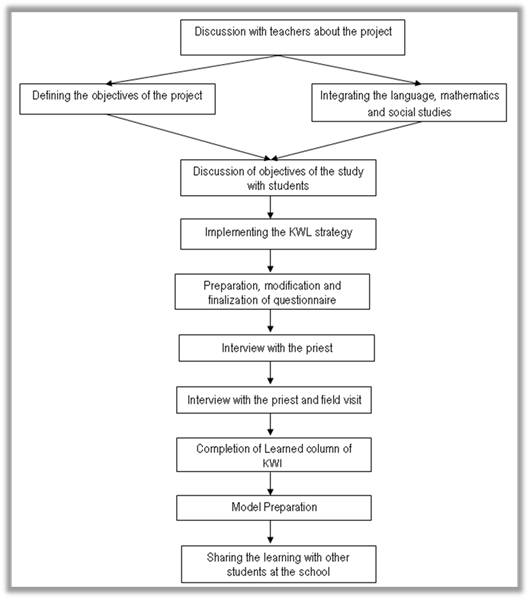
As researchers are teacher educators in the school where we have conducted this research, we started working with them from the beginning of every new session. We have been working in this school since 2015 in teacher professional development and school-based curriculum development process. Each year, we initiate our work through the national curriculum framework. We started with the focus that schools need to be “encouraged to conduct practical classes by developing appropriate teaching materials and made them capable in the development and management of teaching materials by using local means and resources” (CDC, 2007, p. 56).
It is important to state that the core agenda is to provide some theoretical and practical ground of activity-based instruction. This program is designed to foster student learning opportunities through active learning processes where students themselves construct their own knowledge based on their own context. Constructivism and contextualized learning are the key terms we carry throughout the year for the program. In the beginning, almost all teachers were teaching students by applying textbook centered approaches where a single book is mistaken as the curriculum. One of the reasons for this problem is that, often, the “teaching in all levels is examination oriented” (NAIDOO, 2004, p. 55). Final written evaluations are only a standard that show students learning throughout the year.
At first, we struggle to establish alternative teaching learning strategies approaches with teachers and school leadership. It took 3 years to bring them to agreement in relationship to how students can learn better through outside classroom activities. We have struggled to make our teachers participants as they incorporate concepts of D´Ambrosio´s Trivium Curriculum[3](ROSA & OREY, 2015) that is used to enhance learning opportunities through their own cultural context and practices where students learn to apply their own cultural practices without knowing formal mathematical structure and knowledge (ROSA & RAIMUNDI, 2019).
The central idea of culturally relevant pedagogies is considered as the heart of instructional activity (ROSA & OREY, 2016). A culturally relevant pedagogy can play an important role in the teaching and learning of mathematics because it can help teachers to make mathematics learning contextual and creates activities where students relate to their own culture and everyday life (SHARMA & OREY, 2017). Through this work, we have come to believe that history and culture have significant value for both children and mathematics educators. In so doing, we started creating links between traditional practices happening in society where both children and educators belong to academic mathematics.
According to D’Ambrosio (1985), human civilization and the history of mathematics have strong relationships. In this context, history of mathematics can hardly be distinguished from the broad history of human behavior in definite regional contexts, recognizing the dynamics of exchanges, and this is fundamental as well for mathematics education in diverse contexts. Every small community has its own values and practices that allow children to survive and effectively flourish and develop into successful adults.
Educational systems throughout history have focused on two purposes: to transmit values from the past and to prepare for the future (D’AMBROSIO, 1985). The key aspects of the Trivium Curriculum, composed by literacy, matheracy and technocracy, are the key concepts we try to make teachers understand before they get involved in the school-based curriculum. The school has hired us as researchers to develop their own context-based curriculum where national curricular objectives for particular grades are guidelines.
Initially, we were not sure about the actions that were designed and the outcomes we expected in correct order. But as we continued with this project, this project helped the teachers to develop their understanding of the different meanings of literacy and matheracy with the recent development of technological advancements. As novice researchers we also had lots of struggles in making connections with our cultural practices and day to day school mathematics.
In order for teachers to implement a sense of cultural connection, they need knowledge of and respect for the various traditions and languages in their communities (ROSA & OREY, 2011). In the beginning, teachers were not receptive of our ideas in relation to the connection between school mathematics with cultural practices because they were used to memorization and drill activities found in the textbooks.
In so doing, we created stories that assisted teachers in developing understanding and to value the history of mathematics and human civilization. Modern mathematics is a product of human civilization that cannot go alone. From the pre-hunting ages to the present date, the way we have all come to live and learn and have become the shared sociocultural heritage that has an enormous impact on the way we interact, live together and solve problems (D’AMBROSIO & ROSA, 2008). In reflection, we saw how day to day learning is attached to culture and history where we are creating myths and modern development.
This project also helped practitioner teachers in the program to deconstruct their traditional beliefs on teaching and learning mathematics and supported them as they started to construct new ways to connect to school mathematics with their own cultural practices. D’Ambrosio (2006) affirms that mathematical ideas, procedures, and practices are developed in different cultures in accordance to common problems that are encountered within a cultural context. The most crucial stage for the teachers in the project was when they began to realize the importance of culture, mathematics and social development.
Teachers also wanted to connect mathematical ideas with sociocultural aspects, but they found themselves in a dilemma as to how the school’s teaching learning activities could be connected to local cultural artifacts. It soon became important for teachers to understand uses of the student’s own unique social and cultural contexts, and how they might increase possibilities that enabled them to play a vital role in constructing their own mathematical knowledge process (SHARMA & OREY, 2017). To connect with this idea, it took around 3 months to prepare them for designing an activity.
At first, we conducted workshops and training for teachers. After training we asked them to start with small projects which took only 2 or 3 days for their children to complete. It was also a complicated stage because not all teachers were able to produce expected results. For that, the researchers started to develop some projects for teachers to develop their instructional development. It took another 15 days for us to map the activities to national curricular goals and to develop activities which helped their children to learn excepted outcomes set in curriculum. We asked them to design some excursion activities by using local cultural heritage.
In this regard, one of our sample projects was conducted for grade 4 students to find the numbers and shapes used in Patan Durbar Square. Children constructed some drawings and presented them in the school after a month. It was a first model, for the project and created excitement for our teachers to connect mathematics to their heritage though it was not covered in our excepted fundamentals for connecting and finding cultural mathematical practices. We kept motivating and encouraging the teachers as they were performing culturally relevant pedagogical action for their children.
Finally, we wanted to manage this research with Rato Machchhindranath Jatra[4] where different peoples from the Kathmandu valley perform for its cultural and religious value. It takes more than a month to travel and complete the jatra, so we asked teachers’ to integrate curriculum from social studies, language and mathematics for the project. We worked together with teachers’ to develop the complete project with the aim for developing model and finding the meaning of numbers used to construct the chariot of Machchhindranath rath.
After consulting with school leadership we created an authentic community of people who are involving in the process of developing a model of Machchindranath. Cycle based interviews, observations and continuous discussion with our teachers showed all of the participants how they were able to design a project for grade five students.
Normally, the teachers’ role in our school context is to educate the student, evaluate their performance and perform some other responsibilities asked by school administration. Chalk and talk approach is the traditional form of instructional method for mathematics teachers in Nepal. Taking children outside the classroom is considered as a big burden by teachers. The majority of Nepalese mathematics teachers take content knowledge that is only needed for teaching to the curricular objectives. In this context, preparing teachers in three connected skills — content, pedagogy and guiding philosophy — became the process for our participant teachers. The majority of Nepali mathematics teachers we work with need to learn how to listen to and address their students’ voices (SHARMA & NEUPANE, 2014).
Most mathematics teachers in Nepal consider formal mathematics as mathematics but they are mostly unaware that it has come as part of human civilization as well is part of the context of the local culture and community as well. The most challenging part of this stage was to create clear pedagogical distinctions between culturally relevant pedagogy and other establish pedagogies in the instruction. In relation to the pedagogical work developed in schools, the “views of pedagogy within the literature on ethnomathematics are compatible with work on culturally relevant pedagogy” (HART, 2003, p. 42), which examines the cultural congruence between students’ communities and schools.
The method of measurement, shapes and counts and mathematical operation which we now use in mathematics evolved with human civilization. Educators need support in order to increase their understanding in relation to the value of local culture and its application to classroom mathematics. Rosa (2010) recommends that teachers also need to develop a general sociocultural knowledge about their students’ development as well the ways that socioeconomic circumstances such as language and culture influence and shape mathematical performance. According to Sharma and Orey (2017), as a sole responsible person in the classroom, teachers should develop a clear sense of their own ethnic, social, and cultural identities in order to understand and appreciate those of their students.
Methodology describes the process of how outcomes were achieved. Here, in this research we follow the ethnographic process to develop the outcomes of our research. Furthermore, we consider that this research investigated a contemporary phenomenon of the school, which is a case according to Yin (2014). Therefore, our study design aligns with similar ethnographic case studies because of the involvement of the participants and the researcher in this investigation for a long period of time. Our involvement enabled us to both see and incorporate the learner and researchers perspectives on math trail activity done by school children.
Ethnographic case study, as defined by Yin (2014), is a method of study that enables researchers to engage in research with participants in order to develop the information generation process. We have generated layers of understanding and perspectives on mathematics learning and teaching process through the development of the proposed activities. It also helped us to present the world of Newar community deeply. The roots of ethnography lie in anthropological studies that focused on studying social and cultural aspects of small communities.
As a researcher and participant we both try to create a neutral environment in which our influence on our research is minimized and/or reduced. Being as researchers we engage in both learning and fieldwork activities of students and teachers. In accordance to Wolcott (1995), fieldwork is a form of inquiry that requires researchers to be immersed personally in the ongoing social activities.
The research was conducted in a school with teachers and students to enhance the mathematical learning of the learners. Here, Machindranath represents a cultural artifact of local Newar community that the students and teachers have been observing and celebrating for longer period of time. In this context, we find it relevant to conduct our research though cultural lens by developing, according to Hammersley and Atkinson (2007) and Fetterman (2010), ethnographical procedures. This research method focused on studying social and cultural aspect of the Newar community.
Further, this aspect of study provided the researchers to personally immerse in engaging with the learning accumulated by the students and teachers during the development of the process of the fieldwork (WOLCOTT, 1995). In this regard, Barbour (2010) states that ethnography allows researchers to explore the cultural interaction and meaning of small communities, such as Newar community.
It is important to state that, in this study, data was collected that allowed us to acquire information produced by the students during the development of the fieldwork portion. The observation students made in relation to the Machindranath chariot, the feelings they had during the accomplishment of the fieldwork, the interview and their interaction with stakeholders, as well the models and pictures students have elaborated after the observation helped us to gather important information about this case study.
It was here that we felt confident to encourage the teachers at our school to developing competencies through the lens of an ethnomathematics program. We aimed towards developing a project on cultural heritage for Nepali students. An ethnomathematics program suggests that culture is one of the most important resources for teaching and learning of mathematics (ROSA & OREY, 2011). At this point, we found that teachers were involved in searching mathematical ideas involved in the cultural heritage artifacts like shapes, measurements, and numbers. One of the teacher participants asked, “How could the people in those primitive times measured exactly a square or a circle?”. We took this ethnomathematical teaching perspective as a key point of approach in delivering mathematics for empowering students in their learning experiences.
According to Rosa and Orey (2013), this approach aims to draw from the students’ cultural experiences in using them as vehicles to make mathematics learning meaningful as well as to provide them with insights of mathematical knowledge as embedded in their sociocultural environments. For this, we took the perspective of an ethnomathematics program for developing our teachers’ competencies, where teachers build strong connections to mathematics, culture, and over all human endeavor. This is the point when we realized how teachers’ competencies on mathematics were becoming stronger in relation to content and to their own culture and civilization.
We took the perspective of an ethnomathematics program to assist practitioner teachers to connect our own particular context of mathematics, culture, history, anthropology, pedagogy, and linguistic diversity to develop an integrated school-based curriculum. We also emphasize that empowerment is another important sociocultural element in which we wanted to see in the development of teachers’ performance and hopes.
The etymology of ethnomathematics is composed of the prefix ethno that refers to sociocultural contexts and, therefore, includes language, jargons, and codes of behavior, myths, and symbols. The derivation of mathema means to explain, to know, to understand, and to perform activities such as ciphering, measuring, classifying, ordering, inferring, and modelling. And finally, the suffix tics is derived from techné and has the same root as arts and techniques (D’AMBROSIO, 1985). In this case, ethnomathematics relates to the members of distinct cultural groups who have identified themselves by their cultural traditions, codes, symbols, myths, and a specific way of reasoning, inferring, and modelling (ROSA & GAVARRETE, 2017).
This idea perfectly assisted us to work with this particular Newar community in which they have their own perspective to perform their Rato Machchhindranath Jatra. However, without mathematical modelling it is not possible to build a rath over centuries because local people have developed their own way of translating it through the elaboration of ethnomodels. For example, figure 3 and 4 show a model the building ofMachchhindranath.


Therefore, Rosa and Orey (2015) argue that by using ethnomodels, students try to understand the world by means of explanations that are organized as procedures, techniques, methods, and theories, as they aim to explain and deal with daily facts and phenomena. Here we saw that local cultural practices and religious meanings of constructing rath (chariot). We believe that meaningful contexts for local activities make for easy and sensible connections with classroom mathematics and have been shown to bring a change in the attitudes of our teachers and students in the process of teaching and learning of mathematics (UNESCO, 2008). To support this notion we worked in linking students’ context with the classroom mathematical content. According to Rosa and Orey (2010), when we teach mathematics without linking context; it ultimately does not help to create and develop a meaningful use of mathematical ideas; and it may devalue the cultural context of our diverse communities.
In this context, Rosa (2010) affirms that this process of teaching mathematics through cultural relevance and ethnomathematical perspectives use a culturally project-based context to help students to know more about their own reality, culture, and society by providing them with the mathematics content and approaches that enabled them to master academic mathematics. The idea of mathematics in cultural practices involves the designing of tasks that are contextualized in the cultural heritage and are based on different ways of knowing to help us reflects on certain mathematical notions as well as on the nature of mathematical knowledge. However, h this pedagogical work is realized in the classrooms may be still problematic in regard to the misconceptions related to ethnomathematics as a program.
Rosa (2010) also states that in culturally relevant mathematics pedagogy, teachers construct bridges between the home culture and school learning of the students, where it promotes the background, experience and knowledge of learners. Under this circumstance, Rosa and Gavarrete (2018) state that a modification of mathematics curriculum is necessary because it admits a wider possibility for mathematical thinking and investigation that is based on diverse cultural practices. Yet, the challenge is how to enlist this cultural strength in schools.
Project-based learning has great impact on education in a globalized world historical context. Project-based learning has proven its strength in diverse settings in various cultures around the world (CHAKRABARTY & MODAMED, 2013). However, here in Nepal, we are trying to extend its strength by adding our unique cultural context and diversity in it because a unique or standardized teaching process has not yet been able to address all the expected learning achievements in our country. Here our project-based learners helped their students to know more about their own reality, culture, and society by providing them with mathematics content and the approaches that enabled them to master academic mathematics (ROSA, 2010).
In so doing we asked a question: How can we make mathematics teaching and learning processes more relevant with the application of cultural practices and realities by using student prior knowledge? To answer this question, we realized that cultural aspects of mathematics are more valuable in designing a project for learning experiences. Therefore, cultural project-based learning (CPBL) has been introduced for the development of instructional activities.
Our teachers were expressing their excitement towards the project on Rato Machchhindranath because we had a long history of working with them for CPBL. We developed a set of fundamental aspects and expectations in relation to the project in the different cycles of training, workshops, pedagogical orientation, and outlines. For the students and teachers alike, the project site was familiar. Students, teachers, and school administration were feeling excited for the project because it is a grand cultural project for integrating mathematics, language, social studies, and technology, and for the learning outcomes. The school administration called a meeting with parents and community to make them aware of what their children and school were doing and to share the context for the project. Lots of questions came from the parents and communities about their view of formal mathematics. An orientation program assisted them to realize how mathematics without context makes almost no or less meaning to most learners.
In accordance to Sharma (2012), if our children learn to see mathematics only from a formal-foreign perspectives, they may come to see that our culture is less powerful and might not work with mathematics, or even worse, that they cannot work with the mathematics that they see in school. With support of this view, the parents also developed positive views on CPBL and its importance in learning. They also understood that projects have a component of integrating authentic context and real-world problems (O’NEILL & JELLEY, 2014), however, they can miss sociocultural notions of teaching and learning, as well, they may not always be culturally relevant.
Our classroom reflected diverse community elements found in society where children are from and represent the different ethnic groups and geographical locations, which means that they all carry different cultural values in the classroom settings. Projects-based learning alone may not satisfy children's perceptions towards any project they are involved in. Hence, we introduced CPBL to capture each student’s cultural perspectives in the project.
On the other hand, our experience with this project demonstrated how initially the children in the project were not concerned about CPBL, at the same time they were curious in relation to the process of doing outlined activities for the project. Children did not care about what they were going to learn from the project, but later on they shared what changes they felt and saw during and after project.
Formalized school education in our country is divided into three different levels namely: the primary, lower secondary, and secondary. The focus of primary level education is more on learning in the local context, similarly, the lower secondary education is more focused towards learning the National context, and international context is placed for secondary level students. As mentioned earlier, the Machindranath is a local god of the people in the Kathmandu Valley, and the Lalitpur district traditionally celebrates this festival. This is why we decided to integrate this project for learners at the primary level. After finalizing the level of the students in relation to the challenges that came to integrate the content and concepts of the level to the project, the teachers and the researchers sat together to outline the content in the different objectives of the curriculum and we came up to the following objectives to be fulfilled. According to these objectives, students are able to:
· Know the festivals being celebrated in the community and participate.
· Have mutual cooperation with community, neighbors and society.
· Distinguish different shapes.
· Estimate and measure the length, breadth and height of different places.
· Calculate the perimeter area and volume of different objects.
· Calculate the equivalent and mixed fractions.
· Extract information from the data tabulated data.
· Identify the characteristics of matter.
· Know about different local technologies.
After having the visit to the Machindranath and interview with the priest in charge, the students were surprised to know about different facts in relation to Machindranath. Figures 05 and 06 show students visiting Machindranath and interviewing the priest about the chariot.


At the first glance of the Machindranath, they were surprised to see how this extremely tall chariot is built. Initially, they did not see more than the conical shaped tall chariot head and the 4 giant wheels. Figure 7 shows the wheel of the chariot of the Machindranath.
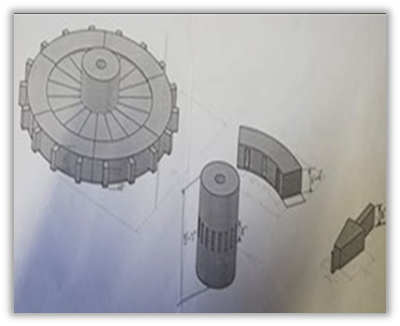
But, after an inquiry with the priest about the importance of the height and the structure of the chariot, they came to know that the height of Machindranath is 32 hands long, which is approximately equal to 48 feet. And the wheels are made in such a way that that each one round of the two front wheel covers, approximately, equal distance to the height of the Machindranath. This means that the wheel is about 16 hands (approximately 24 feet) in its circumference.
According to the priest, although the chariot is said to be built for more than 1000 years, it involves very precise elements of engineering and mathematics. The 32 hand tall chariot is balanced with the 32 hand long log used in between the 4 wheels towards its front side. This log is considered as the symbol of the snake and is called Dhama. Figures 8, 9 and 10 show the log measurement and the log preparation of the chariot, as well the Dhama.



This chariot is built in a such way that it will still remain in balance if it tilts by up to 60 degrees. The priest further added that actually the Machindranath has a conical shape but is built it by using a number of cubical shapes inside in order to make it almost nine stories tall. But, the most interesting part is no metal nails can be used in it, only pieces of wood can be used to hold the frame of the chariot together.
On the inquiry the students asked about the number of priests who worship Machindranath. It was explained that there are 32 priests who worship Machindranath. 31 priests are selected by the members of the priest family one is a Machindranath himself. He also shared one of the interesting facts about the worship of Machindranath that the priest has to stay in the chariot for the whole month because “The priest who stays will sleep inside the small cabin made for the Machindranath and will put his leg towards the God” (Interview with Nabin Bhramacharya-the priest of machindranath).
We also observed how the chariot has a balcony in the form of a square with 8 hands in each side comprising the 32 hands in perimeter. Why always 32? One of the students asked the priest and he replied that the number 32 has a cultural value because it represents the 32 Gunas of Machindranath. Although, Machindranath represents the demon family he was the smallest and 108th son of them having all the godly qualities (Gunas). Hence, each part of the chariot represents the 32 Gunas of Machindranath. Mathematical skills involved in this ethnomodel include the:
Ÿ balance because of the height of the chariot is equal to the length of the Dhama.
Ÿ use of numbers in making Machindranath chariot.
Ÿ use of shapes in Machindranath chariot.
Ÿ estimation and measurement.
It is also important to state here that in order to build the chariot mostly the shape involved in this construction is cuboids. After that the outer most part of the chariot is covered with ropes to make it look like conical shape. Another important information is that non-standard measurement is involved in Nepalese communities.
The findings of the students suggest that they have gained various learning experiences through observation and interview about Machindranath. The students not only have learned mathematical concepts, but they have also gained their strength in understanding the cultural aspectos of the festival that they have been celebrating since longer period of time.
The cultural project-based learning activity of Machindranath chariot applied in this research has been able to develop the critical thinking ability of the students. In the conventional classroom-based mathematics teaching and learning the students just learn what is being told not through exploration (RUSEFFENDI, 2006 cited in HUSNAENI, 2016). However, by avoiding the conventional methods of teaching students, teachers get opportunities to explore their own solution and develop their critical thinking skills (HUSNAENI, 2016).
Here, the students at the field came to know the height of Machindranath chariot is 32 hand tall and the Dhama is equal to the height of the chariot, as well that the circumference of the wheel is half of it, and the side of the balcony is one fourth of the chariot. Then, they found out that each measure comprises to become the factors of the 32, that is, 32, 16, and 8. But, if students have learned only these concepts in classroom, their learning would have just limited to knowing the number and its properties and factors. However, by studying the chariot they observed how the concept of factors and fractions has been applied to build such an architectural cultural artifact.
Similarly, when students were exposed to the Machindranath chariot and had an interview with the priest they also got learned that 32 do not only have mathematical value since it has our cultural value as well. The 32 represents the number itself, that is, the 32 qualities of an individual, which is considered Godly in our Hindu literature. Furthermore, the students might not have posed the question why only 32? in the classroom as regular mathematics classrooms defines the number only as number because there is no any such flexibility to understand it in any other sense. This breakthrough of the number sense of the students can be gained through making mathematics more culturally sensitive.
Similarly, it is noteworthy that students who participated in this research has gained the understanding that non-standard method of the hand measurement has been used by our ancestors at least before 1100 years from when the chariot festival has started. Students since grade 1 through 3 are given an idea of the non-standard measurement such as measuring through the use of their fingers. Bitta and haat (hand), but the students had never seen and or were never shown by any one that the particular structure had been prepared through those kind of non-standard length measurement.
Knowing this application of mathematics in our own culture definitely provided the students the ownership of a basic mathematical concept. This perspective is aligned to the concepts developed by Rosa and Orey (2011) who claim that when mathematics is considered as a cultural construct it disproves the idea of universality of mathematics. The other mathematical concepts that emerged during the students engagement in understanding the Machindranath chariot was the knowledge about different shapes and its uses in our own culture.
After making the visit and interviews with the priest, the students were encouraged to make an ethnomodel of the chariot. The students used different materials they found in their locality to build this ethnomodel. For example, some of the students used bottle caps to represent the circular wheel, and cardboard paper was used to represent the square base of the chariot. Students also observed that the Machindranath has a conical shape and they used grasses because the chariot is colored in green. These procedures initiated the process of using local materials in mathematics. According to Naveira (2005), ethnomathematics-based projects help to increase demonstrations of cultural identity of the members of different cultural groups. Although, the chariot they have made is not a true proportionate ethnomodel, the students used estimation and measurement techniques to prepare their model. Figure 11 shows students making a model of the Machindranath.

The model of the chariot they prepared is tall and is decorated with what looks like the Machindranath. Furthermore, the wheels and the cuboids the students used to represent the balcony are similar to the chariot. Finally, the Dhama they used seems quite equal in size to the chariot. This indicates that students enhanced their skills in estimation and measurement through making the model of the chariot.
By reflecting about the development of these activities, one of the teacher reflected that:
I have never practiced activities like the Machindranath Project before. In the beginning, I was much puzzled as to why our consultants/ trainers asked me about linking school curriculum with community-based activities like Rato Machindranath Jatra. It was very difficult to me to map my mathematics classroom activities with the Machindranath Chariot. I was completely out of the track but the trainers helped me to design a project which taught me to connect cultural artifacts with curricular activities. After getting several training and workshops for excursion activities I came to realize that I was a traditional teacher. I have never thought about local technologies and mathematical knowledge, which serves our children for better understanding the learning process. I was also thinking about student performance and convincing parents and how it can be a big challenge for me to deliver what I mean to do. I have visited several times in the community to get the real idea for this math trail activity. It took around a month for me to understand the project and how we are supposed to deliver it to the students. When I understood the basic activities, I started to help my students to learn the complete process of projects, its objectives, procedure and the final presentation (assessment). During the process I got help from my school administration, teacher trainer, principal, and the students. Without them it would not had been possible to perform such activities, which is helping our children to learn better with ritual practices with community. I am hopeful that I will be designing activities to connect local mathematical knowledge and the curricular objectives in future as well. Although, the project itself had unique activities that we have been performing in our school. The most difficult part is making students understand the concept of mathematics in our culture. I felt very difficult when I was asking my students to model the Machindranath. They did what they found in the excursion activity, but the most important part I missed them to prepare is the exact proportional ratio for complete chariot building process. During the process, I felt that we have chosen the lower grade students for the Machindranath project. Perhaps, that is the most difficult task I couldn’t accomplish in this process because of students lower age, mathematical knowledge, and skills.
As well, after developing these activities, one of the students reflected that:
I really enjoyed participating in the Machindranath Jatra from school. We met with the people who are building the chariot and they were very kind in showing their work to us. When we visited the Machindranath chariot we saw that although it looks like a conical shape it is made from cuboids of nine stores. One of the surprising things is that they do not use any nails in building the chariot. The Machindranath chariot is too big in its size and is pulled by a number of people with a big rope. I measured the height of the wheel and I could only reach the half of it. Then, I asked the person who is working on building the chariot and he said that it is about 8 feet tall and the circumference is about 24 feet. I enjoyed learning the mathematics with the community people.
In this regard, Orey and Rosa (2008) have stated that through the application of cultural integration in mathematics learning the students develop their representations and procedures into their cognitive systems. In this context, this example represents the students’ ethnomodel of the Machindranath chariot.
The results of this research indicate that the learning mathematics can be made meaningful by using cultural artifacts in the process of teaching and learning mathematics. Thus, the students’ ability to understand mathematical concepts was enhanced through cultural connections. Students who used to think mathematics as a foreign and dehumanized subject has now started to see mathematics in their own culture and celebrations.
Similarly, these results also identify that the process not only helps students, but also the teachers and educators who were involved in this process gained a different point of view of mathematics. It is inferred that the absoluteness of mathematics has now been broken and the students and teachers who got involved in this math trail activity can now see mathematics in other cultural activities as well.
Furthermore, the meaning of numbers came to discussion beyond their representation. The numbers that students and teachers have been using as an absolute value has now been revised through the development of this process. Now students know that numbers have different meanings in different cultures and they have emerged long before any mathematicians came into existence. This indicates that students’ mathematical knowledge has been enhanced through the application of cultural pedagogy in mathematics classroom.
Similarly, we the researchers came to the conclusion that the students’ mathematical skills can be enhanced through the use of cultural artifacts in the classroom activities. Learning was made meaningful by connecting the Machindranath chariot festival to the development of students’ curricular activities. Thus, students and teachers who used to think that solving problems and drilling mathematical exercises given in the textbooks have now been widen through the conduction of this project.
Similarly, the students and teachers who have been celebrating the Machindranath festival for a long time had explored new processes of learning of mathematics and culture. This research outlines that school mathematics needs a vision that concerns the mathematical literacy that provides skills and abilities necessary for the local and global citizenship in order to develop competencies to perform a two-way border crossing (SHARMA, 2012). Working on this concept, the details of Machindranath chariot that students explored in their visits and interviews help to introduce them to the mathematics that is present in our culture and festivals that we have been celebrating for years.
It became a new experience for teachers to learn to clarify the concepts of mathematics through different projects and to make it visible to the students. It is important to state that in this project in regard to the chariot, students observed and explored 3D shapes, found areas and volumes. What was most powerful is that all participants experienced how people in our community are not primitive, simplest, or as backward as is reflected in the textbooks. Rather, the ancient generations had developed precise skills and mathematical knowledge that they reflected through the engineering and designing of different monuments and cultural artifacts.
https://periodicos.ufop.br/revemop/article/view/2465/3164 (pdf)












