



Artigos
A inserção de textos originais na disciplina de História da Matemática a partir de um problema do documento Sea Island Mathematical Manual
The insertion of original texts in the discipline of History of Mathematics from a problem in the document Sea Island Mathematical Manual
La inserción de textos originales en la disciplina de Historia de las Matemáticas a partir de un problema en el documento Sea Island Mathematical Manual
Revemop
Universidade Federal de Ouro Preto, Brasil
ISSN-e: 2596-0245
Periodicidade: Frecuencia continua
vol. 3, 2021
Recepção: 02 Dezembro 2020
Aprovação: 28 Dezembro 2020
Publicado: 01 Janeiro 2021

Resumo: O objetivo deste estudo é apresentar uma proposta de aplicação do texto original contendo o problema 1 do Sea Island Mathematical Manual na disciplina de História da Matemática. O estudo se caracterizou como uma pesquisa bibliográfica e documental. Para aplicação do problema 1 foi reservado um momento na disciplina de História da Matemática na Universidade Estadual do Ceará. Essa aplicação mostrou a possibilidade de inserção de textos históricos em sala de aula, como uma forma de mobilizar conhecimentos matemáticos por meio de situações práticas presente neste problema. Além disso, possibilitou aos discentes inferirem questões sobre que conhecimentos matemáticos poderiam ser utilizados para resolvê-lo. Desta forma, essa pesquisa visa colaborar com demais estudos que se propõem a inserir documentos ou textos originais em sala de aula.
Palavras-chave: Sea Island Mathematical Manual, Documentos e textos originais, História da matemática, Ensino de matemática.
Abstract: The aim of this study is to present a proposal for the application of the original text containing the first problem of the document Sea Island Mathematical Manual in the discipline of History of Mathematics. The study was characterized as a bibliographic and documentary research. And for the application of problem 1, a moment was arranged in the discipline of History of Mathematics at the State University of Ceará. This application showed the possibility of inserting historical texts in the classroom, as a way to mobilize mathematical knowledge through practical situations present in this problem. In addition, it allowed students to infer questions about what mathematical knowledge could be used to solve it. Thus, this research aims to collaborate with other studies that propose to insert original documents or texts in the classroom.
Keywords: Sea Island Mathematical Manual, Original documents and texts, History of mathematics, Mathematics teaching.
Resumen: El objetivo es presentar una aplicación del texto original que contiene el problema 1 del Manual Matemático Sea Island en la disciplina de Historia de las Matemáticas. El estudio se caracterizó por ser una investigación bibliográfica y documental. Para la aplicación del problema 1 se reservó un momento en la disciplina de Historia de las Matemáticas de la Universidad Estatal de Ceará. Esta aplicación mostró la posibilidad de insertar textos históricos en el aula como una forma de movilizar el conocimiento matemático a través de situaciones prácticas presentes en esta problemática. Además, permitió a los estudiantes inferir preguntas sobre qué conocimientos matemáticos podrían usarse para resolverlo. Así, este busca tiene como objetivo colaborar con otros estudios que proponen insertar documentos o textos originales en el aula.
Palabras clave: Manual matemático de Sea Island, Documentos y textos originales, Historia de las matemáticas, Enseñanza de las matemáticas.
1 Introdução
A educação matemática e a história da matemática nos últimos anos vem sendo tratadas como campos de pesquisa independentes, cada uma com seus objetos de conhecimento. Garcia (2009) aponta a educação matemática como uma área autônoma e que tem como objeto de estudo a pesquisa, o ensino, a aprendizagem, entre outros. Entre outros estudos que fazem abordagens desses objetos são Pinheiro (2016), Radford (2016), Paiva (2019), entre outros.
Assim a história da matemática também é considerada como um campo de conhecimento, oferecendo distintos recursos e estratégias que podem auxiliar na construção do conhecimento matemático. Dentre eles, podemos destacar os métodos de multiplicação das civilizações antigas, problemas práticos, documentos etc.
Segundo Chaquiam (2017), a inserção de fatos históricos em sala de aula podem ser uma alternativa dinâmica para introduzir um conteúdo matemático, visto que esse aluno pode construir uma visão da matemática de uma forma humanizada, que se desenvolveu para resolver problemas do cotidiano, de modo a possibilitar conhecer as distintas necessidades de cada civilização na antiguidade.
De acordo com Mendes e Chaquiam (2016) os professores precisam estar cientes do tipo de história que querem levar para sala de aula, de modo a extrair dela aspectos que favoreçam a explicação de porquês matemáticos. E ampliem as possibilidades e as inquietações dos alunos para que eles possam realizar estudos futuros em torno dos aspectos históricos que permeiam os conteúdos matemáticos (MENDES; CHAQUIAM, 2016).
Para Roque (2012) e Saito (2015) a história da matemática sendo considerada com um campo de pesquisa nos possibilita ter acesso a diferentes recursos históricos de determinados períodos que podem contribuir para compreender o desenvolvimento do conhecimento matemático em diferentes épocas.
Desta forma, com vista a incorporar elementos da história no ensino de matemática, encontramos nos recursos que ela oferece, no caso os documentos, essa oportunidade. É importante destacar que segundo Saito (2015, p. 27), os documentos não são apenas livros e tratados, “[...] mas também cartas, manuscritos, minutas e outros documentos não só escritos, mas também aqueles da cultura material, tais como instrumentos, monumentos, máquinas etc.”.
Então, dependendo da abordagem historiográfica dada a história da matemática na pesquisa, esse documento, tende a receber outras denominações. Na perspectiva historiográfica tradicional, quando o passado é visto com os olhos do presente, Pereira e Pereira (2015) e Silva (2020) afirmam que pode ser denominado por fonte histórica ou “[...]como uma fonte documental extraída diretamente do contexto em questão ou, de forma mais geral, uma produção original escrita” (SILVA, 2020, p. 6). Ambas as nomenclaturas rementem a “[...] qualquer material produzido, em determinada época que sirva para comprovar e inferir dados históricos” (SILVA, 2020, p. 6). Ou seja, essas fontes são ricas porque trazem em si aspectos do período no qual estavam inseridas.
Enquanto, na perspectiva historiográfica atualizada, quando nos remetemos ao passado para compreendermos aspectos matemáticos presentes no período, Saito (2015) ressalta que esses documentos são considerados para além daqueles materiais escritos, considerando, objetos, máquinas, instrumentos, entre outros. Todavia, Silva (2020, p. 9) ressalta que
[...] um documento não é apenas um papel com partes escritas, tudo pode ser um documento. Dentro deles, pode-se ter o que é chamado de “texto original”, que é a sua parte escrita. Como um documento pode ser uma obra grande, tratando de diversos assuntos, são esses textos que são selecionados dentro deles para serem usados em sala de aula na busca da articulação entre história e ensino de matemática.
Fundamentado na concepção de Silva (2020) e deixando claro que a perspectiva historiográfica adotada neste estudo é a perspectiva historiográfica tradicional, iremos utilizar o documento Sea Island Mathematical Manual, escrito por Liu Hui, no século III, E.C. Ele é composto por nove problemas que envolvem situações práticas que permeavam o período no qual estava inserido, entre elas, voltadas para o campo da agrimensura, abrangendo medições de comprimento, largura, altura e profundidade. No entanto, nesse estudo será utilizado apenas o texto original que apresenta o problema 1.
Esse documento como podemos ver pelo próprio título se encontra em inglês. Infelizmente não tivemos acesso a sua versão em chinês ou em alemão que teriam sido produzidos bem antes do século XX (KANGSHEN; CROSSLEY; LUN, 1999). Assim, nesse estudo esse documento se caracteriza como uma fonte primária, pois segundo Silva (2020, p. 10) “[...] fonte primária é aquela que está sendo analisada, independentemente de ser um documento ou um texto original, é a principal fonte de informação”, ou seja, mesmo não tendo em mãos o documento em chinês, a nossa fonte principal de investigação é o Sea Island Mathematical Manual.
Partindo dele é que vamos ao encontro de demais materiais que possam auxiliar na compreensão do mesmo e de seu contexto. Nesse âmbito esses materiais se caracterizam como fontes secundárias que “são livros-textos com narrativas históricas, interpretações, reconstruções, artigos científicos, livros específicos, entre outros” (PEREIRA; PEREIRA, 2015, p. 69). Essas fontes secundárias são aquelas que já passaram por algum tratamento, ou interpretação por parte de outros e que foram escritas sob a concepção deles.
De acordo com Fossa (2019) há duas razões para a inserção de leituras de textos históricos em sala de aula, a primeira seria: já que conhecimentos matemáticos estão permeando a cultura humana, então seria de extrema importância levar esse aluno a se aproximar do conhecimento de documentos daquela cultura matemática; o segundo argumento seria de que a construção do conhecimento a partir de documentos tende a realizar “(i) à atividade construtiva do conhecimento, (ii) à natureza social do conhecimento e (iii) à dialética da apropriação do objeto matemático” (FOSSA, 2020, p. 130).
Levando em consideração as diversas vantagens de utilizar documentos e textos originais em sala de aula, foi então que pensamos neste estudo. Todavia, não contemplamos muitos trabalhos desenvolvidos em torno desse tema, por isso realizamos uma busca na Biblioteca Digital Brasileira de Teses e Dissertações (BDTD) e no Catálogo de Teses e Dissertações da Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), fazendo uso das palavras-chave, “Sea Island Mathematical Manual”, “matemática chinesa” e “matemática na china antiga”, na qual constatamos nenhuma pesquisa que tratasse a respeito de elementos da obra Sea Island Mathematical Manual.
Posteriormente, realizamos uma outra busca na plataforma internacional JSTOR, fazendo uso das mesmas palavras-chave, todavia não foram encontrados estudos que tivessem relação com os problemas do Sea Island Mathematical Manual, de modo a explicitar uma experiência em sala de aula. Apenas pudemos identificar artigos que tratam de temas próximos ao abordado neste estudo, no entanto, com um caráter teórico, com os de, Ang e Swetz (1986), Lay-Yong e Kangsheng (1986), Straffin Junior (1998). As buscas foram realizadas no dia 26 de dezembro de 2020 e não houve delimitação de ano para o período de busca. Desta forma, diante desse cenário é notável a falta de estudos que englobem aspectos da obra Sea Island Mathematical Manual de modo a voltá-la para a sala de aula, quer seja na Educação Básica ou no Ensino Superior, de modo a explorar conhecimentos matemáticos por meio de aspectos da história.
Portanto, esse estudo tem como objetivo apresentar uma aplicação do texto original contendo o problema 1 do documento Sea Island Mathematical Manual na disciplina de História da Matemática no ensino superior, como uma forma de mobilizar conhecimentos matemáticos por meio da história da matemática. Assim, o artigo se encontra dividido em quatro partes: uma apresentação geral sobre Sea Island Mathematical Manual e o problema 1; o caminho metodológico percorrido dentro do estudo; uma descrição a respeito dos dados coletados mediante a aplicação do problema 1 do documento Sea Island Mathematical Manual na disciplina de História da Matemática; e por fim, as considerações finais a respeito do estudo realizado.
2 Um panorama geral do documento Sea Island Mathematical Manual de Liu Hui (220 E.C – 280 E.C)
O Sea Island Mathematical Manual é um documento chinês escrito por Liu Hui (220 E.C – 280 E.C) em 263 E.C., pós Dinastia Han. Inicialmente, esse documento era apenas comentários de Liu Hui sobre um documento maior, intitulado Nine Chapters on the Mathematical Art (KANGSHEN; CROSSLEY; LUN, 1999). De acordo com Ang e Swetz (1986) Liu Hui era do estado de Wei e ficou conhecido no século III E.C, porém nada mais se sabe sobre sua vida.
O Nine Chapters on the Mathematical Art, escrito por volta do século I E.C, durante a Dinastia Han (206 a.E.C - 220 E.C) é uma reunião de vários trabalhos de matemáticos do período e apresenta grande parte do saber envolvido na época (BERTOLINI, 2007). Além disso, esse documento é formado por nove capítulos que envolvem conhecimentos matemáticos aplicados com diversas finalidades.
Segundo Qian (1963, apud ANG; SWETZ, 1986), Liu Hui foi um dos comentaristas do Nine Chapters on the Mathematical Art, mais especificamente, do nono capítulo, intitulado Gougu, que fala dos triângulos retângulos, pois observou uma falha nele. Ele escreveu, então, um novo capítulo, que ele chamou de chong cha, ou seja, “diferenças duplas” com o intuito de explicá-lo mais adequadamente. Esse comentário acabou se tornando um capítulo, só depois, o nome foi modificado para Sea Island Mathematical Manual [i] (ANG; SWETZ, 1986).
Além disso, Liu escreveu nesse capítulo, nove problemas, baseado nos problemas elementares de agrimensura[ii] contidos no nono capítulo do documento Nine Chapters on the Mathematical Art, porém com um grau de dificuldade maior (KATZ, 2010). Esses problemas foram separados do Nine Chapters on the Mathematical Art, durante a dinastia Tang (618 E. C - 907 E.C), tornando-se independente e intitulado Sea Island Mathematical Manual (KANGSHEN; CROSSLEY; LUN, 1999).
De acordo com Kangshen, Crossley e Lun (1999, p. 518, tradução nossa), “Os nove problemas do manual tratam da medição de uma distância, e o trabalho está escrito no estilo tradicional dos antigos tratados matemáticos chineses. Primeiro o problema é apresentado, então a resposta é dada e isto é seguido pelo método”[iii]. Adiante segue o Quadro 1 com o objetivo de cada problema.
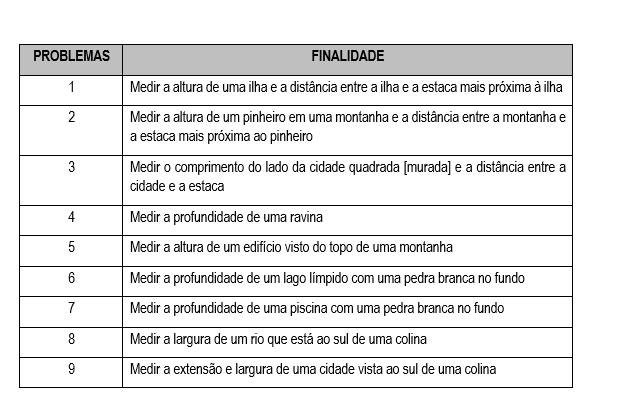
Observa-se no Quadro 1 que, além de medir distâncias, ou seja, comprimento e largura, os nove problemas também medem alturas e profundidades. Esses nove problemas “[…] envolvem o uso da teoria do triângulo retângulo e resultam em uma variedade de técnicas e fórmulas para determinar distâncias a pontos inacessíveis” (ANG; SWETZ, 1986, p. 99, tradução nossa)[iv]
Segundo Kangshen, Crossley e Lun (1999, p. 525, tradução nossa), o método das diferenças duplas (chong cha), utilizado na resolução dos problemas do manual, foi chamado assim, pois “[...] Liu observou os objetos duas ou mais vezes” [v] e “[...] no processo de seus cálculos, ele aplicou as diferenças dos lados correspondentes dos triângulos retângulos duas vezes [...]”[vi]. Liu Hui ressalta em seu prefácio que,
Eu escrevi a Regra das Diferenças Duplas com alguns comentários, de modo a facilitar nossa busca pelos significados originais. Isto é acrescentado ao Capítulo sobre Triângulos Retângulos (Capítulo 9). A medição da altura envolve dois pólos, e medição de profundidade, dois gnomons. Se outro ponto for adicionado, deve-se observar três vezes; uma quarta observação é necessária se o ponto adicional não estiver no mesmo plano que os outros pontos (KANGSHEN; CROSSLEY; LUN, 1999, p. 54, tradução nossa)[vii].
Percebemos que para chegar à solução dos problemas Liu utilizava-se de instrumentos, tais como os pólos[viii] para medir alturas e os gnomons[ix], para medir profundidades. A Figura 1 ilustra melhor esses instrumentos. De acordo com Ang e Swetz (1986), Liu Hui disse que esse método das diferenças duplas, não foi criado por ele. Esse mesmo método já havia sido empregado anteriormente, só não com a denominação de diferenças duplas intitulada por Liu Hui.
Nesse estudo iremos tratar do problema 1 do Sea Island Mathematical Manual, que fala sobre a determinação de medidas lineares relacionada a comprimento e altura como pode-se ver no enunciado e no método de resolução apresentado por Kangshen, Crossley e Lun (1999, p. 539 a 541),
[Problema 1]
Agora inspecione uma ilha do mar. Erga dois pólos da mesma altura, 3 zhang, de modo que os pólos dianteiro e traseiro estejam separados por 1000 bu. Eles estão alinhados com o cume da ilha. Mova-se para trás 123 bu do pólo da frente, avistando ao nível do solo, e perceba que o cume da ilha coincide com a ponta do pólo. Mova-se para trás 127 bu do pólo traseiro, avistando ao nível do solo, e perceba que o cume da ilha também coincide com a ponta do pólo. Diga: Qual é a altura da ilha e sua distância do pólo [frontal]?
Resposta: A altura da ilha é de 4 li 55 bu; é de 102 li 150 bu do pólo [frontal].
Método: Multiplique a distância entre os pólos pela altura de um pólo como dividendo. Tome a diferença na distância dos pontos de observação (xiangduo) como divisor e divida. Adicionando o quociente à altura de um pólo, obtenha a altura da ilha α. Para encontrar a distância da ilha até o pólo frontal, multiplique a distância entre os dois pólos (biaojian) pela distância movida para trás como divisor. Divida para obter a distância entre a ilha [cume] e o pólo [frontal] em li.β[x]
É importante destacar que o Sea Island Mathematical Manual foi encontrado no décimo capítulo do livro The Nine Chapters on the Mathematical Art Campanion and Commentary, de autoria de Kangshen, Crossley e Lun (1999). E os autores acrescentaram aos nove problemas, os comentários de Li Chunfeng et. al. Ou seja, o problema, a resposta e o método de resolução são de Liu Hui, enquanto qualquer acréscimo a esses três tópicos, são comentários a mais.
O primeiro problema traz dois questionamentos: qual a altura da “ilha do mar”; e qual a distância entre a ilha e o pólo (estaca) frontal, ou seja, o pólo mais próximo à ilha. Entretanto, antes de levantar essas questões, Liu Hui prepara toda a situação, informando como e onde devem se posicionar os pólos e o agrimensor (aquele que vai realizar a medição) (Figura 2).
Na Figura 2 é perceptível a formação de triângulos retângulos. Ademais, Kangshen, Crossley e Lun (1999) afirmam que para a resolução do grande número de problemas, tanto no nono capítulo do documento Nine Chapters on the Mathematical Art quanto do Sea Island Mathematical Manual, foram utilizadas as propriedades de triângulos semelhantes.
Além disso, observa-se que para realizar as medições é preciso dois pólos de mesma altura (na cor azul), sendo 3 zhang, a uma distância de 1000 bu um do outro (na cor vermelha), alinhados com o pico da ilha. O agrimensor deve se deslocar conforme a orientação dada, de modo que ele perceba, por meio de sua visão, ao nível do solo, que o ponto mais alto do pólo da frente coincida com o pico da ilha e, depois, que o ponto mais alto do pólo de trás, também coincida com o pico da ilha.
Segundo Kangshen, Crossley e Lun (1999), foram perdidos os diagramas de Liu Hui, que explicavam mais detalhadamente todo o seu método. Portanto, temos no século XXI, somente a situação problema, a resposta e o método de cada um dos nove problemas. Por isso, o método apresentado por Liu Hui é único, de tal modo que não se sabe o motivo dele ter utilizado tais procedimentos, ainda que estudiosos tenham tentado compreender (KATZ, 2010). No entanto, percebe-se a utilização das “diferenças duplas”, pois todos os nove problemas
[...] requerem dois ou mais avistamentos observacionais para resolver situações problemas envolvendo dois conjuntos de triângulos semelhantes onde existe semelhança dentro dos conjuntos, mas não entre eles. A relação de similaridade dá origem a dois conjuntos de proporções que devem ser resolvidos simultaneamente, e esse parece ser o foco da técnica de solução de chong cha. (SWETZ, 1992, p. 28, tradução nossa)[xi].
Assim, o método das diferenças duplas (Chong cha) consiste em observar duas ou mais vezes essas situações, que formam dois conjuntos de triângulos semelhantes. Além disso, nesse problema são fornecidos alfa (α) e beta (β), referindo-se aos comentários de Li Chufeng at al. Esses comentários auxiliam na compreensão do método, porém, não explicam o motivo de Liu Hui ter se utilizado desse método específico, para resolver o problema. Isso pode ser visto a seguir,
(α) Li et al .: Aqui a cimeira da ilha refere-se ao topo de uma colina. Os polos (as estacas) são as pontas das hastes verticais. A linha de visão passa pela ponta do pólo e pelo cume da ilha. A distância 123 bu do pólo é o comprimento da sombra do pólo frontal. A linha de visão também passa pela ponta do pólo traseiro e pelo agrimensor. A distância é 127 bu do pólo. A diferença entre as duas distâncias dos pólos é chamada xiangduo, que é considerada como divisor. A distância entre os pólos, 1000 bu, é chamada de biaojian. Multiplique [por] a altura de um pólo para o dividendo. Divida e adicione a altura do pólo para obter a altura da ilha, 1255 bu. Existem 300 bu em um li, então um recebe 4 li 55 bu, a altura da ilha.
β) Li et al .: No método, é melhor dizer: multiplique a distância entre os pólos pela distância do pólo frontal, dando 123 000 [exatos] bu. Tome a diferença dos pontos de observação (xiangduo), 4 bu, como divisor. Divida para obter 30 750 bu. Divida novamente por 300 bu em um li para ter 102 li 150 bu, a distância entre a ilha e o pólo [frontal]. (KANGSHEN; CROSSLEY; LUN, 1999, p. 540 - 541, tradução nossa) [xii].
Em alfa, tem-se, por exemplo, alguns esclarecimentos, como: explica que a distância de 123 bu corresponde a medida da sombra do pólo frontal; define os nomes xiangduo, que corresponde a diferença entre 127 bu e 123 bu, e do biaojian que corresponde a distância entre os pólos; que 300 bu corresponde a 1 li, etc. Já em beta, podemos observar que o método é reescrito com outras palavras, para ficar mais claro.
3 Percurso metodológico
Esse estudo se caracteriza como uma pesquisa qualitativa, pois segundo Sampieri, Collado e Lucio (2013, p. 34), tem como foco uma vertente interpretativa com relação aos indivíduos envolvidos na pesquisa, com ênfase no sentido de suas ações, “[...] principalmente dos humanos e de suas instituições (busca interpretar aquilo que vai captando ativamente)”.
Em relação aos procedimentos, realizou-se no primeiro momento um estudo sobre o que são documento e textos originais e a respeito da versão comentada por Kangshen, Crossley e Lun (1999) do documento Sea Island Mathematical Manual, escrito por Liu Hui, no século III E.C, mais especificamente, do texto que consta o problema 1.
Esse momento teve como objetivo conhecer: o tipo de documento que tínhamos em mãos; a finalidade desse documento e de seus problemas para a época; sobre o que trata; período no qual estava inserido; quem o escreveu; entre outros aspectos. Assim, nesse primeiro momento esse estudo se caracterizou como uma pesquisa bibliográfica e documental, pois segundo Marconi e Lakatos (2003, p. 183) no caso da pesquisa bibliográfica,
[...] abrange toda bibliografia já tornada pública em relação ao tema de estudo, desde publicações avulsas, boletins, jornais, revistas, livros, pesquisas, monografias, teses, material cartográfico etc., até meios de comunicação orais: rádio, gravações em fita magnética e audiovisuais: filmes e televisão. Sua finalidade colocar o pesquisador em contato direto com tudo o que foi escrito, dito ou filmado sobre determinado assunto, inclusive conferências seguidas de debates que tenham sido transcritos por alguma forma, quer publicadas, quer gravadas.
Enquanto a pesquisa bibliográfica abrange diversos materiais que já passaram por algum tratamento e foram publicados, com o intuito de deixar o autor ciente sobre o conhecimento divulgado, “a pesquisa documental vale-se de materiais que não recebem ainda um tratamento analítico, ou que ainda podem ser reelaborados de acordo com os objetos da pesquisa”, se encaixando desta forma, na parte que envolve o estudo do Sea Island Mathematical Manual (GIL, 2002, p. 48).
Esse manual contém dez problemas, no entanto, nesta pesquisa, somente o texto que contém o problema 1 foi tratado. Em relação a ele foi realizado um estudo mais detalhado sobre o seu enunciado, resposta e descrição do método de solução, para que posteriormente fosse aplicado em sala de sala de aula. Em relação a aplicação fizemos uso de acordo com Silva (2020), de um dos critérios para a utilização de textos originais em sala de aula sendo ele, “quando utilizar o texto original?”. Nesse momento planejamos a aplicação posteriormente a aula que tratou sobre as matemáticas na China antiga como forma de aprofundar os conteúdos explanado na sala de aula.
No segundo momento, após conhecermos todos os detalhes do problema, preparamo-nos para aplicá-lo na disciplina de História da Matemática, no turno da tarde, ministrada no 5o semestre (fluxo 2019.1) e no 6o semestre (fluxo 2019.1), ambos em vigor no semestre 2019.1, na Universidade Estadual do Ceará (UECE), campus Itaperi. A aplicação aconteceu durante uma aula que tratava sobre os conhecimentos matemáticos da China antiga.
4 Uma visão geral da aplicação do problema 1 do documento Sea Island Mathematical Manual na disciplina de história da matemática
Essa aplicação na disciplina de História da Matemática ocorreu no semestre 2019.1, no qual a turma foi organizada em duplas, de modo que cada uma delas recebeu uma folha contendo o texto correspondente ao problema 1 do Sea Island Mathematical Manual, juntamente com a resposta e o método de resolução utilizado por Liu Hui. Além disso, foi disponibilizado duas observações α e β colocadas no documento por Kangshen, Crossley e Lun (1999), mas que foram produzidas por autores como Li Chunfeng, entre outros, por volta de 656 E. C. É importante ressaltar que todos esses elementos até aqui citados foram disponibilizados em inglês.
Ademais no verso da folha continham quatro questões, sendo elas: 1) traduzir o enunciado, a resposta e o método do problema 1 contido no Sea Island Mathematical Manual; 2) compreender e explicar a solução do problema 1; 3) resolver o problema 1 utilizando nossa matemática atual; 4) realizar comparações entre as duas soluções (similaridades, diferenças, etc.).
A aplicação aconteceu durante uma aula que tratava sobre os conhecimentos matemáticos da China antiga. No entanto, devido o tempo de aula ser de 2h/a (100 minutos), permitimos que os alunos levassem a atividade para casa e que entregassem na próxima aula, ficando com ela em mãos durante três dias. No início da disciplina de História da Matemática tínhamos 26 alunos, por volta do momento dessa aplicação estavam presentes apenas 16 discentes. A desistência ou trancamento se dá muitas vezes pelo fato de que alguns alunos começam a sentir dificuldades por conta de não terem cursados outras disciplinas anteriormente, como geometria plana e espacial, cálculo diferencial e integral, entre outros.
No dia da entrega final, das oito duplas formadas apenas cinco delas, no caso 10 alunos, entregaram a atividade, sendo manuscrita ou digitada. De acordo com o Quadro 2 é possível ver quais as duplas responderam todas as questões. Para isso elaboramos a seguinte legenda: RC = Resposta completa: RP = Reposta Parcial: -- = Não respondeu.
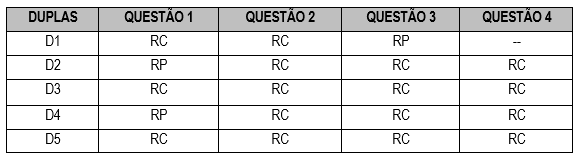
De acordo com o Quadro 2, apenas as duplas D1, D2 e D4 não responderam por completo alguns dos itens, na sequência serão pontuados os itens que ficaram incompletos. Em relação a questão 1) que trata sobre traduzir o enunciado e a solução do problema 1 contido no Sea Island Mathematical Manual, todas as duplas realizaram esse procedimento de maneira correta, apesar de algumas delas esquecerem alguns detalhes. Todavia não demonstraram nenhuma dificuldade nesse momento.
Isso mostra que apesar do problema ser disponibilizado em inglês e alguns alunos não dominarem essa língua, não houve dificuldades ou prejuízo no primeiro momento da resolução. Alguns deles até ressaltam no momento da entrega que o problema lhe impulsionou a sair da sua zona de conforto e buscar recursos com dicionários, aplicativos ou consultar colegas, para a realizar a tradução correta desse problema.
Isso pode ser visto na dupla, D3 que realizou além do solicitado, escrevendo uma introdução sobre o documento, The Nine Chapters on the Mathematical Art, Liu Hui e o apêndice Sea Island Mathematical Manual. Todavia algumas duplas não se atentaram para traduzir pontos importantes que seriam fundamentais mais a frente, como é o caso da D2 e D4, que não traduziram a resposta do problema 1 e as duas observações α e β feitas por Kangshen, Crossley e Lun (1999), respectivamente.
Na questão 2) cujo objetivo era compreender e explicar a solução do problema 1, todas as duplas responderam. A dupla D5 descreveu toda a solução enfatizando que Liu Hui apresenta no decorrer do método fórmulas matemáticas para resolver problemas semelhantes no período, envolvendo situações de medições de altura e comprimento. A dupla D4 durante o processo de resolução ressaltou que,
Ao propor esse problema e resolve-lo, Liu Hui não deixa nítido quais conhecimentos foram necessários para que este tenha sido resolvido, no entanto, a partir do que fora explicado no texto, é possível entender que o autor já conseguia compreender noções que hoje conhecemos como semelhança de triângulos, porém de uma maneira menos teórica, e ao que parece, usando o auxílio do sol e da sombra (D4, 2019).
É possível perceber que a dupla D4 realiza inferências de que no século III E.C., provavelmente Liu Hui teria conhecimentos de semelhanças de triângulos, porém, não sendo definidos por essa denominação. Isso é possível, mas para constatarmos a veracidade, é necessário que em um outro estudo seja realizado uma pesquisa aprofundada em torno do contexto e da época no qual foi produzido o Sea Island Mathematical Manual.
As duplas D1, D2 e D3 responderam essa questão envolvendo outros procedimentos além do que Liu Hui orientou. A equipe D1 apresentou o seguinte desenho nessa questão (Figura 3).
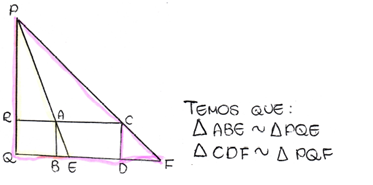
A partir da Figura 3 é possível perceber que a dupla representou a situação apresentada no problema 1 por meio de triângulos retângulos e estabeleceu uma relação de proporção entre os seus lados, dois a dois, de modo que ao final do cálculo chegaram nos procedimentos indicados pelo método de Liu Hui. Enquanto, a equipe D2 e D3, se utilizaram de outros conhecimentos como podemos ver na Figura 4.
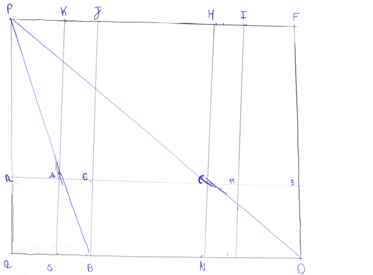
Apesar da Figura 4 está distorcida a dupla parte da comparação entre as áreas dos retângulos QRCN e CEFH que são iguais. A dupla parte do pressuposto de que a imagem está contida em um retângulo QDPF e que ( ) sendo a diagonal, dividi o retângulo em dois triângulos retângulos iguais. Em seguida, a partir dos polos (( ) e ( )) são levantadas linhas perpendiculares e paralelas a eles, de forma que a figura fique toda subdivida em retângulos e triângulos.
Vejam que nesse item 2) a partir da leitura da resolução do problema proposta por Liu Hui os alunos levantaram diferentes questionamentos sobre distintos conhecimentos matemáticos que poderiam ser manipulados nessa resolução, como semelhança de triângulos ou a comparação entre áreas. Cada dupla apontou um modo de vislumbrar essa solução, optando por não irem pelo mesmo caminho, isso mostra aspectos de uma situação rica de conceitos matemáticos, pois não é nosso objetivo querer que o aluno compreenda exatamente a resolução, mas a partir dela coloque suas primeiras impressões e construa o melhor caminho a ser tomado para solucioná-la.
Na questão 3) destinada a resolver o problema 1 utilizando nossa matemática atual, todos os discentes realizaram os cálculos. No caso da dupla D1, eles vincularam a resposta a questão 2), dando destaque ao uso da semelhança de triângulos de modo sucinto. Enquanto, as duplas D2, D4 e D5, resolveram também diretamente por semelhança de triângulos, porém com mais detalhes. A seguir escolhemos um desenho que melhor representa a resolução dessas duplas que consideraram os mesmos triângulos (Figura 5).
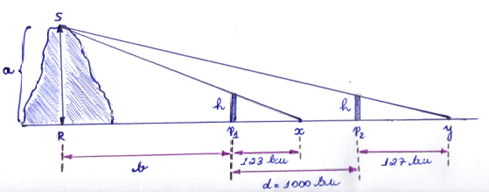
Essas duplas consideraram os triângulos semelhantes ∆hP2y e ∆SRy e o ∆hP1x em relação ao ∆SRx. Todavia não relataram qual o caso de semelhança identificado no momento dos cálculos. Mas a partir desse procedimento iniciaram o processo de proporção entre os lados dos triângulos, realizando substituições, de modo a encontrarem os resultados fornecidos por Liu Hui. A dupla D3, considerou a semelhança entre outros dois triângulos, no entanto, constatamos ao final uma resposta sem explicação lógica em relação ao resultado encontrado, desta forma, não iremos expor aqui.
Nesse item 3) note que os alunos começaram a constatar que o melhor procedimento a ser tomado para a resolução do problema seria a semelhança de triângulo, isso fica nítido quando todos optam por esse caminho. Essa parte do estudo mostra a possibilidade que o professor tem, de retomar o ensino de alguns conteúdos matemáticos, entre eles, semelhança de triângulos por meio de situações históricas, mostrando que a matemática não é apenas teórica, mas, muitos dos processos de cálculos foram utilizados para resolução de problemas práticos na antiguidade.
Em relação a questão 4) que trata sobre realizar comparações entre as duas soluções (similaridades, diferenças, etc.), apenas a dupla D1 não respondeu. Na sequência podem ser contempladas no Quadro 3 as explicações de cada uma das demais duplas.
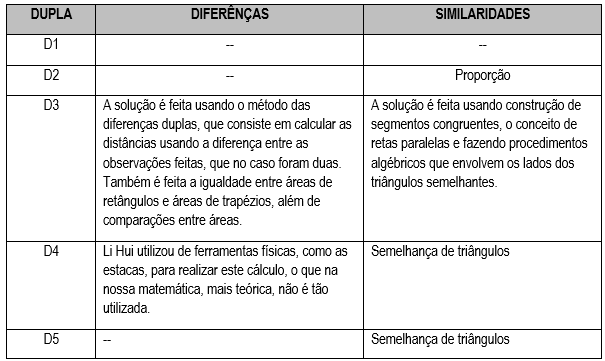
De acordo com o Quadro 3, somente duas duplas manifestaram quais as diferenças entre os métodos utilizados. Em relação a dupla D3 destacaram a utilização do “método das diferenças duplas” que seria o método de resolução apresentado por Liu Hui. E ainda acrescentaram a possibilidade de comparação entre áreas de retângulos e de trapézios. Enquanto a dupla D4, ressaltaram que os procedimentos dos chineses eram bem mais práticos, do que a matemática do século XXI, com teoremas e fórmulas.
Assim, a aplicação na sala de aula do ensino superior do problema 1 do Sea Island Mathematical Manual visou mostrar as possibilidades de mobilizar conhecimentos matemáticos por meio da resolução de problemas históricos e conhecer a forma como os alunos reagem no primeiro momento com situações desse tipo. Esse contanto inicial é fundamental para termos uma visão geral do que deu certo, ou precisa ser modificado, ou adaptado, para melhor chegar na sala de aula para o nossos discentes, inclusive quando tratamos da Educação Básica.
5 Considerações finais
O Sea Island Mathematical Manual chegou até nós em uma versão em inglês, comentada por Kangshen, Crossley e Lun (1999). Esse documento apresenta situações que envolvem a resolução de problemas práticos. Todavia, esses problemas de agrimensura trazem consigo métodos de resoluções que não são comuns à primeira vista, demonstrando que o documento não tinha nenhuma finalidade pedagógica de ensinar um conteúdo matemático, mas de instruir os estudiosos do período na resolução de problemas envolvendo medições.
O texto original que consta o problema 1 e que foi aplicado na disciplina de História da Matemática, se torna interessante para o estudo em sala de aula porque através dele os discentes perceberam que os conhecimentos matemáticos utilizados por Liu Hui não são os mesmos utilizados no século XXI. Chegando à conclusão de que cada período desenvolve suas próprias matemáticas, destacando assim suas especificidades, no qual aspectos de ordem social, econômica, cultural, política, entre outros, influenciam na produção do conhecimento.
Além disso, essa atividade aplicada no ensino superior nos possibilitou contemplar a quantidade de conhecimentos matemáticos que podem ser mobilizados por meio de um determinado problema, como por exemplo, algumas duplas ressaltaram que bastava utilizar semelhança de triângulos para chegar no resultado, outras utilizaram a comparação entre áreas de figuras planas, entre elas, quadrado, retângulo e trapézio para se obter o resultado final.
Assim, essa pesquisa buscou apresentar um estudo envolvendo documentos, em especial, textos originais para a mobilização de conhecimentos matemáticos, além de contribuir com outros estudos que estão articulando o uso de documentos em sala de aula, na educação básica ou na formação inicial e continuada de professores. Desta forma, esse estudo não para por aqui, pois visamos em um outro momento explorar outros problemas do Sea Island Mathematical Manual de modo a atrelá-los a uma teoria para a implementação em sala de aula.
Referências
ANG, Tian Se; SWETZ, Frank J.. A Chinese Mathematical Classic of the Third Century: the sea island mathematical manual of liu hui. História da Matemática, v. 13, n. 2, p. 99-117, 1986.
BERTOLINI, Marcel Vinhas. Aspectos da Matemática Chinesa: O 'Nove Capítulos'. In: III Simpósio de Iniciação Científica e Pós Graduação IME-USP, 2007, São Paulo. Anais do III Simpósio de Iniciação Científica e Pós Graduação IME-USP, 2007. v. 1. p. 1-2.
CHAQUIAM, Miguel. Ensaios temáticos: História da matemática em sala de aula. Belém: Sociedade Brasileira de História da Matemática, 2017. 241 p.
FOSSA, John Andrew. Lectura de textos históricos em el aula. Revista Paradigma, v. XLI, n. extra 1, p. 116 – 132, abril. 2020.
GARCIA, Vera Clotilde Vanzetto. Fundamentação teórica para as perguntas primárias: O que é matemática? Por que ensinar? Como se ensina e como se aprende? Revista Educação, Porto Alegre, v. 32, n. 2, p.176-184, ago. 2009.
GIL, Antonio Carlos. Como elaborar projetos de pesquisa. 4. ed. São Paulo: Atlas, 2002.
KANGSHEN, Shen; CROSSLEY, John N.; LUN, Anthony W. C.. The nine chapters on the mathematical art: Companion and commentary. Beijing: Oxford University Press, 1999.
KATZ, Victor J. História da Matemática. Lisboa: Oficinas Gráficas de A.Coelho Dias, S.A., 2010. 1117 p.
LAY-YONG, Lam; KANGSHENG, Shen. Mathematical Problems on Surveying in Ancient China. Archive For History Of Exact Sciences, v. 36, n. 1, p. 1-20, 1996.
MARCONI, Marina de Andrade; LAKATOS, Eva Maria. Fundamentos de Metodologia Científica. 5. ed. São Paulo: Editora Atlas, 2003. 310 p.
MENDES, Iran Abreu; CHAQUIAM, Miguel. História nas aulas de matemática: fundamentos e sugestões didáticas para professores. Belém: Sbhmat, 2016. 124 p.
PAIVA, Jussara Patrícia Andrade Alves. A Teoria da Objetivação e o desenvolvimento da orientação espacial no ensino-aprendizagem de geometria. 2019. 209 f. Tese (Doutorado) - Curso de Programa de Pós-Graduação em Ensino de Ciências e Matemática, Centro de Ciências Exatas e da Terra, Universidade Federal do Rio Grande do Norte, Natal, 2019.
PEREIRA, Ana Carolina Costa; PEREIRA, Daniele Esteves. Ensaio sobre o uso de fontes históricas no ensino de Matemática. Revista de Matemática, Ensino e Cultura, Belém, v. 10, n. 18, p. 65 – 78, 2015.
PINHEIRO, Ana Cláudia Mendonça. Concepção e desenvolvimento de uma formação continuada de professores de matemática baseada na Sequência Fedathi. 2016. 138 f. Tese (Doutorado) - Curso de Programa de Pós-Graduação em Educação Brasileira, Faculdade de Educação, Universidade Federal do Ceará, Fortaleza, 2016.
ROQUE, Tatiana. História da matemática: Uma visão crítica, desfazendo mitos e lendas. Rio de Janeiro: Zahar, 2012. 511 p.
RADFORD, Luis. The theory of objectification and its place among sociocultural research in mathematics education. Revista Internacional de Pesquisa em Educação Matemática, Rio Grande do Sul, v. 6, n. 2, p. 187-206, ago. 2016. Disponível em: http://www.luisradford.ca/pub/The%20Theory%20of%20Objectification%20and%20Sociocultural%20Research_Radford_Ripem_2016.pdf. Acesso em: 20 jul. 2020.
SAITO, Fumikazu. História da matemática e suas (re) construções contextuais. São Paulo: Editora Livraria da Física, 2015.
SAMPIERI, Roberto Hernandez; COLLADO, Carlos Fernández; LUCIO, María del Pilar Baptista. Metodologia de Pesquisa. 5. ed. Porto Alegre, RS: Editora Penso, 2013.
STRAFFIN JUNIOR, Philip D. Liu Hui and the First Golden Age of Chinese Mathematics. Mathematics Magazine, v. 71, n. 3, p. 163-181, jan. 1998.
SWETZ, Frank J.. The Sea Island Mathematical Manual: surveying and mathematics in ancient China. Pennsylvania: The Pennsylvania State University Press, 1992.
SILVA, Isabelle Coelho da; Pereira, Ana Carolina Costa. Definições e critérios para uso de textos originais na articulação entre história e ensino de matemática. Boletim de Educação Matemática – Bolema, Rio Claro, v. 35, n. 69, 2021 (no prelo).
Notas
Now survey a sea island. Erect two poles of the same height, 3 zhang, so that the front and rear poles are 1000 bu apart. They are aligned with the summit of the island. Move backwards 123 bu from the front pole, sighting at ground level, and find that the summit of the island coincides with the tip of the pole. Move backwards 127 bu from the rear pole, sighting at ground level, and find that the summit of the island also coincides with the tip of the pole. Tell: what are the height of the island and its distance from the [front] pole?
Answer: The height of the island is 4 li 55 bu; it is 102 li 150 bu from the [front] pole.
Method: Multiply the distance between the poles by the height of a pole as dividend. Take the difference in distance from the points of observation (xiangduo)(1) as divisor and divide. Adding the quotient to the height of a pole, get the height of the island.α To find the distance of the island from the front pole, multiply the distance between the two poles (biaojian)(2) by the distance moved backwards as divisor. Divide to obtain the distance between the island [summit] and the [front] pole in li.β ”(KANGSHEN; CROSSLEY; LUN, 1999, p. 539 a 541).
(β) Li et al.: In the Method, it is better to say: multiply the distance between the poles by the distance from the front pole, giving 123 000 [square] bu. Take the difference from the points of observation (xiangduo), 4 bu, as divisor. Divide to obtain 30 750 bu. Divide again by 300 bu in a li to have 102 li 150 bu, the distance between the island and the [front] pole” (KANGSHEN; CROSSLEY; LUN, 1999, p. 541).
Ligação alternative
https://periodicos.ufop.br:8082/pp/index.php/revemop/article/view/4671/3619 (pdf)

