



Artículos
El neuroaprendizaje en la enseñanza de las matemáticas: la nueva propuesta educativa
NeuroLearning in teaching mathematics: a new educational proposal
Entorno
Universidad Tecnológica de El Salvador, El Salvador
ISSN-e: 2218-3345
Periodicidad: Semestral
núm. 67, 2019
Recepción: 21 Agosto 2018
Aprobación: 02 Febrero 2019

Resumen: En este artículo se presenta el neuroaprendizaje mediante estudios e investigaciones desarrolladas en el área de las matemáticas. De igual modo, se presenta esta nueva ciencia, la cual no se había pensado antes y que ahora se visualiza con mayor profundidad, en el proceso de enseñanza aprendizaje en el área de las matemáticas. Se le da un gran énfasis a la figura del maestro y a cómo este, al tener un conocimiento bien formado de la manera que aprende el estudiante, puede realizar mejor su labor como docente. Aquí se verá el cerebro como ese órgano del ser humano que puede reforzarse para su propio beneficio a medida que se conoce más. Todos los estudios realizados hasta el día de hoy nos muestran que esta ciencia del ?aprender como aprendemos? irá cambiando la manera de cómo las personas nos enfrentamos y nos enfocamos en la diversidad de problemas y situaciones que debemos conocer para mejorar todo el proceso educativo, psicológico y biológico.
Palabras clave: Cerebro - Funciones, Neurociencias, Aprendizaje, Matemáticas - Enseñanza, Matemáticas - Investigaciones, Memoria.
Abstract: This article introduces Neuro-Learning through sample studies and researches carried out in the area of mathematics. In like manner, it introduces this new science which people had not thought of before; currently, it is more profoundly visualized in the teaching-learning process of mathematics. The figure of the teacher and how his well-formed knowledge on the way students learn are given great emphasis since he can use this knowledge to better carry out his work as a teacher. Here, the brain is seen as the human organ that can be gradually strengthened for people´s own benefit. All studies carried out until today show us that this science of ?learning how to learn? will change the way how people face and focus on the diversity of problems and events that we must know in order to improve the entire educational, psychological and biological process.
Keywords: Brain functions, Neuroscience, Learning, Math Teaching, Research in math, Memory.
Introducción
Qué es el neuroaprendizaje
En varias ocasiones, te has preguntado sobre que es el aprendizaje y cómo el ser humano lo adquiere. Pues se podría decir, desde una vertiente pedagógica, que el aprendizaje es la capacidad que tiene nuestro cerebro de adaptación y reordenamiento en los espacios a los requerimientos ambientales y a los cambios. Nuestro cerebro se desarrolla desde que nacemos hasta que morimos; en todas las etapas de nuestra vida es posible modificarlo, capacitarlo y cambiarlo; las experiencias de la vida lo van moldeando, pero el momento de mayor plasticidad y donde se producen los mayores y más rápidos cambios es en la infancia.
Las experiencias que vivimos en nuestra niñez tienen un impacto decisivo en la ?arquitectura? de nuestro cerebro. El cerebro de un niño de 3 años es 2 veces más activo que el cerebro de un adulto con una elevada actividad intelectual. Por eso es fundamental ayudar a los niños en su desarrollo cerebral, para que optimicen todas sus posibilidades mediante el juego, la curiosidad, la intelectualidad, la dinámica y el respeto a su identidad.
La maduración neurológica es diferente en cada niño. Hay que respetar sus ritmos de maduración, para ayudarles a desarrollarse y crecer con seguridad en sí mismos. En esta etapa, el niño va adquiriendo cierto sentido de qué es lo que realmente necesita y quiere aprender de acuerdo con sus intereses y particulares inquietudes.
En la edad adulta, nuestro cerebro también cambia; tal y como lo usemos así se irá configurando. En el caso de las personas de más edad, se puede retrasar el envejecimiento del cerebro manteniéndolo activo.
Mediante el neuroaprendizaje, se puede optimizar el funcionamiento del cerebro para potenciar los procesos que intervienen en el aprendizaje: atención, memoria, lenguaje, lectura, escritura, razonamiento y emociones.
El neuroaprendizaje es una disciplina que combina la Psicología, la Pedagogía y la neurociencia para explicar cómo funciona el cerebro en los procesos de aprendizaje. El cerebro es el órgano más plástico que tenemos, está en continuo cambio y desarrollo. En el neuroaprendizaje debemos ser conscientes de potenciar los aspectos que intervienen en el aprendizaje; y de que estos se perpetúen por siempre o en el mayor tiempo posible.
Hoy día, el neuroaprendizaje es un tema de gran interés. A partir del acercamiento a esta ciencia, es posible determinar aquellos procesos de aprendizaje adecuados para cada cerebro, favorables durante los períodos de docencia. Las herramientas que permiten reconocer cómo funciona este órgano son útiles en las distintas etapas del estudiante niño, adolescente o adulto.
De igual modo, los programas de enseñanza deben conocer el funcionamiento del cerebro en los estudiantes para así poder planificar sus clases y programas de acuerdo a lo que el alumno puede manejar. Además de que en su contenido provean herramientas que ayuden al docente a manejar las técnicas, de ensenanza habilitando primero los circuitos cerebrales para transmitirlos de forma congruente, es decir, vectores, líneas de fuerza direccionales donde la palabra evoca la imagen adecuada; los sonidos de las palabras, la parte auditiva; la emoción, la sensación vivida; acompañados de movimientos corporales que se integren con las palabras expresadas; las imágenes evocadas, el sonido en armonía con la exposición y la emoción. Ese sentimiento de respuesta que entra al metaconsciente cuando hay congruencia en la personalidad. Esto en la Neurolingüística tiene un valor del 93 % en la comunicación; y del 7 % restante solo lo ocupan las palabras.
La programación neurolingüística (PNL), que sustenta el desarrollo humano en todos los niveles lógicos y neurológicos, en uno de sus tantos principios dice que ?la palabra no es la cosa nombrada sino la imagen evocada?; por eso modifica la palabra aula por ambiente de estudio. Esto de ambiente es aplicable a todo lo relacionado con el desarrollo humano: personal, profesional y organizacional.
Hoy, la adaptación nos permite continuar nuestra evolución. Es el modelo que se ajusta a la necesidad del momento, lugar y personas implicadas, que fortalezcan la identidad del ser humano, pues el siglo XXI está generando la fuerza vital en el metaconsciente del tejido psicosocial colectivo.
La mission de la educación es crear una sociedad humana en la que su mayor activo sean los seres humanos con recursos, los neurohumanos; un capital neurocognitivo social sustentado por una neuroeducación y un neuroaprendizaje de avanzada, con un sistema inteligente redireccionado hacia el desarrollo humano.
El neuroaprendizaje es una disciplina que nació de la conjunción de varias ciencias, como la Neurobiología, la Psicología, la Pedagogía y la PNL entre otras. Lo cual permite que se combinen y fucionen como una ciencia de ayuda directa en los sistemas educativos y en la preparación de los educadores.
Si bien hasta hace dos décadas era muy poco lo que se conocía acerca de cómo funciona y aprende el cerebro, a partir de los años 90 ha habido una explosión tecnológica que permitió empezar a conocer más sobre ?el órgano del aprendizaje?.
Un tiempo atrás, los docentes nos debíamos contentar con los resultados de la observación, ya que mediante ella decidíamos si cierta técnica, estrategia, teoría o escuela de aprendizaje era favorable o no para nuestros alumnos. En la actualidad, contamos con elementos para saber cómo aprende el cerebro humano en general y tenemos herramientas para descubrir cómo aprende cada cerebro. Estas nos posibilitan cubrir todos los estilos de aprendizaje, todas las inteligencias, los distintos canales de representación sensorial y formas de enfrentar desafíos. Estamos convencidos de que ?si un niño no aprende es porque no le estamos enseñando de la manera que él puede aprender? (R. Dunn).
Consideramos que es fundamental capacitar a los docentes con estos nuevos conocimientos, que echan por tierra con
ciertos modelos mentales limitantes, como que el cociente intelectual está determinado al nacer o que el nivel de inteligencia es solo medible mediante las evaluaciones tradicionales; y abren el camino a un liderazgo situacional donde se tienen en cuenta no solo el contexto y el estilo general de los alumnos, sino también a cada alumno en relación con las distintas áreas de aprendizaje.
Finalmente, pero no menos importante, es el área del alfabetismo emocional. Basta mirar a nuestro alrededor para darnos cuenta de que, si bien cada vez nacen chicos intelectualmente más inteligentes, el cociente emocional ha disminuido drásticamente. Por eso me animaría a decir que el enseñar a conocer y a manejar nuestras emociones se ha convertido en una necesidad de supervivencia.
Por todo lo mencionado, no me cabe duda de que el neuroaprendizaje es una herramienta imprescindible para el docente de nuestros tiempos, que sabe que el único camino seguro para un futuro promisorio es contribuir a la formación de seres capaces de autogestionarse y superarse a sí mismos.
Aplicaciones del neuroaprendizaje
¿Te sucede con frecuencia que, después de impartir una lección a tus alumnos, pareciera como si ?mágicamente? desaparece de su mente el conocimiento adquirido?
Es común que tus estudiantes retengan un 10 % de lo que leen, 20 % de lo que escuchan, 30 % de lo que ven, 50 % de lo que ven y escuchan, 70 % de lo que se lee y se discute, y 90 % de lo que se lee, discute y ejecuta.
Pero ¿qué sucede si logramos conectar con la parte neuronal del cerebro que procesa la información y comprender cómo lo hace para desarrollar temas optimizados?
De qué manera nos ayuda el neuroaprendizaje
El neuroaprendizaje busca, con las disciplinas combinadas de la Psicología, Pedagogía y Neuropsicología, explicar cómo funciona el cerebro en los procesos de aprendizaje. Esto nos permite enfocarnos mejor en la forma cómo el cerebro procesa la información y cómo conectar con ella. Ayuda a la manera en que el cerebro puede discernir de aquella información que no le sea útil para su aprendizaje; y comienza un proceso de razonamiento analítico y de
crecimiento de condición neuronal que ayuda al estudiante en el autoaprendizaje.
Neuroaprendizaje: sus bases
La Neurobiología aporta al fenómeno del aprendizaje la posibilidad de encontrar respuestas no solo al cómo somos capaces de incorporar nuevas habilidades, sino también al cómo se constituyen los significados. Cómo se aprenden y retienen los nuevos conceptos y cuáles son las bases neuronales que subyacen a estos procesos.
El aprendizaje consciente (explícito)
El aprendizaje metaconsciente (implícito)
El aprendizaje explícito. El aprendizaje explícito, al ser consciente y voluntario, es una decisión individual. En este sentido, para que el proceso de aprendizaje tenga éxito, es requisito fundamental un óptimo nivel de motivación y compromiso de los que participan. Para eso es necesario implementar una metodología que dé protagonismo al que aprende, es decir, que lo coloque en el centro del proceso.
El aprendizaje implícito. El aprendizaje implícito se manifiesta cuando desarrollamos distintas actividades sin tener conciencia de haberlas aprendido. Este aprendizaje se va incorporando mediante un proceso de experiencia y retroalimentación, durante el cual generamos una especie de competencia no consciente. Una vez que hemos aprendido, no nos detenemos a analizar cómo resuelve nuestro sistema nervioso los problemas que se nos van presentando.
La información que tenemos sobre el cerebro humano, órgano responsable del aprendizaje, se ha visto claramente incrementada debido al desarrollo de las nuevas técnicas de visualización cerebral. Como consecuencia de estas investigaciones recientes, aparece una nueva disciplina en la que confluyen los conocimientos generados por la neurociencia, la educación y la Psicología, que nos pueden aportar información significativa sobre el proceso de enseñanza y aprendizaje. La neuroeducación consiste en aprovechar los conocimientos sobre el funcionamiento cerebral para enseñar y aprender mejor.
Maguire (2000) realizó un estudio donde analizó el hipocampo de los taxistas de Londres, ciudad caracterizada por su amplia red vial. Se comprobó que el tamaño de dicha región cerebral, implicada en el aprendizaje y la memoria espacial, era mayor en los taxistas que en el resto de conductores, además, en los taxistas más expertos era mayor que el de los con menos experiencia.
Implicaciones educativas
El hecho de que cada cerebro sea único y particular (aunque la anatomía cerebral sea similar en todos los casos) sugiere la necesidad de tener en cuenta la diversidad del alumnado y requiere ser flexible en los procesos de evaluación. Asumiendo que todos los alumnos pueden mejorar, las expectativas del profesor hacia ellos han de ser siempre positivas y no les han de condicionar actitudes o comportamientos pasados negativos.
En cuanto al tratamiento de los trastornos del aprendizaje, hay diferentes programas informáticos que han demostrado su utilidad en la mejora de determinadas capacidades cognitivas, como la memoria o la atención. En concreto, Fast ForWord de Scientific Learning Corporation (avalado por Michael Merzenich) es un programa para estudiantes disléxicos que ha ayudado a compensar las dificultades que tienen con el procesamiento fonológico (ver figura 1). Este tipo de entrenamiento continuo mejora la comprensión del lenguaje, la memoria y la lectura.
Las emociones sí importan
Las emociones son reacciones inconscientes que la naturaleza ha ideado para garantizar la supervivencia, y que, para nuestro propio beneficio, hemos de aprender a gestionar (no a erradicar). La neurociencia ha demostrado que las emociones mantienen la curiosidad, nos sirven para comunicarnos y son imprescindibles en los procesos de razonamiento y en la toma de decisiones, es decir, los procesos emocionales y los cognitivos son inseparables (Damásio, 1994). Además, las emociones positivas facilitan la memoria y el aprendizaje (Erick, 2003), mientras que en el estrés crónico la amígdala (una de las regiones cerebrales clave del sistema límbico o ?cerebro emocional?) dificulta el paso de información del hipocampo a la corteza prefrontal, sede de las funciones ejecutivas.
Si entendemos la educación como un proceso de aprendizaje para la vida, la educación emocional resulta imprescindible porque contribuye al bienestar personal y social.
En este estudio internacional, basado en cientos de investigaciones en las que han participado más de 500.000 estudiantes de educación infantil, primaria y secundaria, se ha demostrado que los programas de educación emocional sistemáticos afectan al desarrollo integral de los alumnos: disminuyen los problemas de disciplina, están más motivados para el estudio, obtienen mejores resultados académicos, muestran actitudes más positivas y mejoran sus relaciones.
La novedad alimenta la atención
La neurociencia ha demostrado la importancia de hacer del aprendizaje una experiencia positiva y agradable. Sabemos que estados emocionales negativos, como el miedo o la ansiedad, dificultan el proceso de aprendizaje de nuestros alumnos. Pero, en la práctica cotidiana, han predominado los contenidos académicos abstractos, descontextualizados e irrelevantes, dificultando la atención sostenida, que ya de por sí es difícil de mantener durante más de 15 minutos (Jensen, 2004). A los seres humanos nos cuesta reflexionar, pero somos curiosos por naturaleza; y es esta curiosidad la que activa las emociones que alimentan la atención y facilitan el aprendizaje.
Waelti, P.; Dickinson, A.; Schultz, W. (2001) realizaron un estudio que demuestra que, para optimizar el aprendizaje, no es importante la recompensa sino lo inesperado de esta. Analizando la respuesta de neuronas dopaminérgicas, se comprobó que se activaban cuando el organismo tenía una determinada expectativa; y la respuesta conductual era mejor de lo que se esperaba. De lo anterior, se concluye que, tanto en el nivel neuronal como en el conductual, lo importante para el aprendizaje es la anticipación de la recompensa y no el simple premio.
La práctica continua permite progresar
El cerebro conecta la nueva información con la ya conocida, por lo que aprendemos mejor y más rápidamente cuando relacionamos la información novedosa con los conocimientos ya adquiridos. Para optimizar el aprendizaje, el cerebro necesita la repetición de todo aquello que tiene que asimilar. Es mediante la adquisición de toda una serie de automatismos como memorizamos, pero ello requiere tiempo. La automatización de los procesos mentales hace que se consuma poco espacio de la memoria de trabajo (asociada con la corteza prefrontal, sede de las funciones ejecutivas); y sabemos que los alumnos que tienen más espacio en la memoria de trabajo están más dotados para reflexionar (Willingham, 2011).
Bahrick, H.P. y Hall, L.K. (1991) hicieron un estudio en el que participaron más de 1.000 personas. Se realizó una prueba de álgebra a personas de distintas edades que habían hecho un curso entre un mes y 55 años antes. Se pudo observar que las calificaciones se dividieron en cuatro grupos, atendiendo al nivel de matemáticas mostrado (la línea inferior corresponde a personas con nivel más básico, mientras que la superior corresponde a las personas con nivel más avanzado). Los principiantes obtuvieron porcentajes de respuestas correctas (eje vertical) más bajos; y conforme pasó más tiempo entre la prueba y el último curso de álgebra realizado, en el período que se señala arriba, los resultados fueron peores. Sin embargo, los participantes con nivel más avanzado recordaban el álgebra de la misma forma con el paso de los años (curva prácticamente horizontal), lo que indicaba que el tiempo que se pasaba estudiando la materia era el que determinaba lo que se iba a recordar de esta.
El arte mejora el cerebro
La neurociencia está demostrando que las actividades artísticas, en particular la musical, promueven el desarrollo de procesos cognitivos. La instrucción musical en jóvenes mejora la capacidad intelectual como consecuencia de la plasticidad cerebral, sobre todo en aquellos con mayor interés y motivación hacia las actividades artísticas (Posner, 2008). Además, en algunos niños aparecen correlaciones entre la práctica musical y la mejora en geometría o las capacidades espaciales cuando el entrenamiento es intenso. Por otra parte, el teatro o el baile desarrollan habilidades socioemocionales, como la empatía, y son beneficiosos para la memoria semántica. Por ejemplo, al hablar en público se genera noradrenalina, una sustancia que se sabe que interviene en los procesos relacionados con la atención, la memoria de trabajo o el autocontrol.
Wandell, B. et al. (2008), en una investigación con 49 niños de edades comprendidas entre 7 y 12 años, midieron los efectos de la educación artística (en concreto artes visuales, música, baile y teatro) en la capacidad y comprensión lectora. Y se comprobó que la mayor correlación se daba para el entrenamiento musical (ver figura 6).
Cómo funciona el neuroaprendizaje en las matemáticas
Las matemáticas han sido una de las ciencias que mayor dificultad ha causado al estudiante. Es por esto que las ramas donde los estudiantes tienen que utilizar matemáticas son las que menos estudiantes tienen. En la mayoría de los casos se crea una apatía generalizada sobre la fobia hacia las matemáticas, pues implican llevar al estudiante hasta un razonamiento analítico en donde su cerebro tiene que haber dominado una serie de niveles de pensamiento. Al no haber adquirido la maduración en los anteriores niveles de pensamiento, más difícil se hace la tarea de poder llegar al nivel de pensamiento del razonamiento analítico.
En ( Wynn, 2015) (citado en Fernández, 2010) realizó una serie de experimentos con bebés de 5 meses. En uno de aquellos, enseñó a los bebés un juguete que escondía tras una pantalla. A continuación, los bebés observaban cómo escondía un segundo juguete en el mismo lugar. Al cabo de unos segundos, la investigadora apartaba la pantalla y cronometraba el tiempo que los bebés miraban. Observó que si al retirar la pantalla aparecía un juguete (resultado no posible: 1+1=1) los bebés miraban durante un período de tiempo mayor que cuando aparecían dos juguetes (resultado lógico: 1+1=2). Este tipo de experimentos, que se han repetido en numerosas ocasiones, sugieren que los bebés poseen una capacidad innata para el procesamiento numérico. ¿Aprovecha la educación este sentido innato del cerebro para fomentar un aprendizaje adecuado de las matemáticas? En este artículo analizamos algunos estudios que, utilizando las técnicas modernas de visualización cerebral, nos permiten observar las regiones más activas en la resolución de problemas matemáticos, principalmente numéricos. A continuación, reflexionamos sobre algunos factores críticos en el proceso de enseñanza y aprendizaje de las matemáticas.
El cerebro matemático
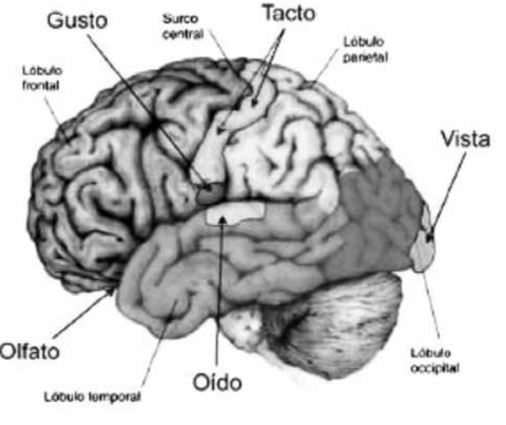
Diversos experimentos muestran una gran activación de los lóbulos frontal y parietal en la resolución de problemas. Stanislas Dehaene y sus colaboradores enseñaron una serie de cálculos a voluntarios bilingües en uno de sus idiomas. Tras el entrenamiento, se les pedía que resolvieran ese tipo de cálculos de forma exacta o aproximada en las dos lenguas. Los investigadores observaron que la resolución de problemas exactos era más rápida en la lengua que utilizaron al aprender los cálculos, aunque utilizaran más la otra lengua en la vida cotidiana. Sin embargo, en los cálculos aproximados (se les pedía a los voluntarios que hicieran estimaciones) no se apreciaban diferencias significativas. En los cálculos exactos se observaba una mayor activación en las áreas del cerebro involucradas en el lenguaje, mientras que en los cálculos aproximados se activaba más el lóbulo parietal de los dos hemisferios.
Analicemos alguna operación concreta. En las multiplicaciones (sabemos que los niños aprenden de memoria las tablas de multiplicar) se activa el giro angular izquierdo, que pertenece al sistema verbal, es decir, son codificadas verbalmente. Sin embargo, al hacer comparaciones o estimaciones se activa el surco intraparietal porque no necesitamos convertir los números en palabras, es decir, son independientes del lenguaje. El hemisferio izquierdo calcula (recordemos que, en la mayoría de personas, al ser diestras, el lenguaje reside en el hemisferio izquierdo), mientras que el hemisferio derecho hace estimaciones.
En relación con la función que desempeña el lóbulo parietal en la representación espacial, hemos escuchado a matemáticos explicar la utilización de imágenes mentales en la resolución repentina de problemas. Esto guarda relación directa con el concepto de insight, que hace referencia a la capacidad de comprender la estructura interna de un problema que, muchas veces, aparece de forma imprevisible. La comprensión de los mecanismos inconscientes que facilitan este tipo de resoluciones tendrá enormes implicaciones en la forma de enseñar, aunque lo que ya conocemos es que para que se produzca el insight se requiere un estado de relajación cerebral. Una razón más para facilitar los estados exentos de estrés en los entornos educativos.
Algunos factores críticos en la enseñanza de las matemáticas
1. Creencias previas y factores emocionales
Comentarios típicos como ?nunca entendí las matemáticas? o ?no se me dan bien las matemáticas? se han asentado, progresivamente, en la mente de muchos alumnos, y recalcan la importancia que tienen las creencias previas y la inteligencia emocional en el aprendizaje. Fomentar un clima educativo que favorezca las emociones positivas (facilitando factores como el optimismo o la resiliencia), en detrimento de las negativas, es tan importante o más que la aportación de contenidos puramente académicos.
La pedagogía utilizada en la fase inicial del aprendizaje de las matemáticas incide directamente en la motivación del alumno. El rechazo inicial provocado en muchos niños guarda una relación directa, en numerosas ocasiones, con una enseñanza basada en infinidad de cálculos mecánicos que coartan el proceso intelectual creativo del alumno y en una representación de la terminología incomprensible para él.
El papel del profesor
Ya hemos comentado que diferentes estudios parecen demostrar que los seres humanos nacemos con un sentido numérico innato. Según Dehaene y Butterworth, dos de los grandes expertos mundiales en el estudio de las matemáticas y el cerebro, la escuela obstaculiza este desarrollo facilitado, inicialmente, por factores genéticos. Dehaene cree que la construcción de los conceptos abstractos ha de iniciarse con la formulación de ejemplos concretos, con la finalidad de estimular el desarrollo del razonamiento intuitivo del niño. Además, la interacción con la mente del alumno requiere la
manipulación de materiales y actividades lúdicas. Los cuales el niño pueda manejar concretamente para luego llevarlo al proceso abstracto.
Ejemplo: La utilización de algunos juegos de mesa puede ser de gran utilidad. En concreto, se ha demostrado que el aprendizaje del ajedrez puede mejorar el cálculo mental, el razonamiento intuitivo, la memoria, la capacidad de abstracción o la concentración.
La recomendación de facilitar el desarrollo intuitivo guarda relación directa con el concepto del insight, en el que la intuición y los mecanismos de resolución inconscientes desempeñan un papel fundamental. El excesivo énfasis en conceptos abstractos, sin utilidad práctica aparente, y la memorización rutinaria de algoritmos perjudica la evolución y motivación del alumno.
Ejemplo: Si pedimos a niños de 6 y 10 años de edad que nos calculen la sencilla operación 6 + 4 ? 4, podemos comprobar que, a menudo, los niños de 6 años responden 6 sin necesidad de realizar cálculo alguno. Sin embargo, los niños de 10 años, que son más expertos, pueden realizar el cálculo en su hoja (6 + 4 = 10, y luego 10 ? 4 = 6).
Por otra parte, los docentes hemos de intentar presentar contenidos abiertos que faciliten el establecimiento de relaciones y la generación de ideas, así como guiar el proceso de evolución del alumno poniendo a su disposición mecanismos de autocorrección que les permitan ser conscientes de sus razonamientos acertados o no. ?¿Qué piensas sobre???. Los docentes deberíamos facilitar procesos de resolución alternativos que fomenten los razonamientos creativos.
Ejemplo: En dos ecuaciones formalmente idénticas como las siguientes, en la segunda se cometen más errores porque aumenta la carga de la memoria de trabajo en las fracciones:
Un ejemplo que demuestra la importancia del análisis de los errores cometidos. En este sentido los errores que comete el estudiante tienen una gran importancia, pues de ahí puede partir el proceso de enseñanza, debido a que los errores cometidos ubican al estudiante en cierto nivel de pensamiento.
Hemos constatado que la localización del conocimiento matemático en el cerebro es complicada porque incluye diferentes circuitos que pueden actuar de forma parcialmente autónoma. Lo cierto es que los diferentes campos de estudio de las matemáticas requieren enfoques dependientes. Por ejemplo, existe una conexión entre aritmética y geometría (pensemos en la visualización espacial de los números utilizados en las operaciones aritméticas básicas). La utilización de diferentes áreas cerebrales en el proceso de aprendizaje diversifica las estrategias pedagógicas, aunque, a pesar de la dificultad, lo que parece claro es que el proceso de enseñanza y aprendizaje de las matemáticas cambiará y deberá considerar la base empírica que aportan las investigaciones en neurociencia. La multimodalidad propuesta por Gallese y Lakoff representa una nueva concepción del pensamiento, que puede acaparar en el futuro un gran protagonismo. Según esta propuesta, el conocimiento matemático (o cualquier otro) está ligado a nuestro sistema sensoriomotor, por lo que no solo pensamos con la ayuda del lenguaje y de los símbolos, sino también mediante los sentidos, es decir, las impresiones sensoriales constituyen el carácter multimodal de los conceptos. Según esta propuesta, la enseñanza tradicional del lápiz y papel no permite una conexión duradera con la experiencia sensorial vivida por los alumnos en los primeros años escolares.
El gran problema con el que nos encontramos los docentes es que los investigadores realizan sus experimentos con una metodología diferente a la utilizada en el entorno académico, lo que dificulta su aplicación en el aula. Ahora bien, en algunos casos, tenemos a nuestra disposición importantes recursos educativos. Un caso concreto es el de la discalculia, que podemos encontrar en niños motivados e inteligentes pero que seguramente padecen alguna anomalía cerebral, normalmente en la región izquierda del lóbulo parietal. El estudio de estas personas demuestra la existencia de problemas, dejando aparte los aritméticos, relacionados con la orientación espacial, el control de sus propias acciones y sobre la representación de su cuerpo, especialmente de los dedos. Esto nos recuerda la forma de contar con los dedos de los niños, y su control, y los gestos que hacen, que conllevan determinadas posiciones corporales. Si la representación de los dedos no llega a desarrollarse normalmente, se pueden originar dificultades en el desarrollo de las habilidades numéricas. La detección de estas anomalías nos permite aplicar mecanismos compensatorios que faciliten una comprensión de las operaciones básicas o de las reglas explícitas más lenta pero
segura. Pero, para ello, hemos de asumir que la inteligencia no es un concepto unitario y que el aprendizaje en cada alumno es diferente. Sea como fuere, seguimos buscando recursos para diseñar la práctica docente con soportes empíricos; y los principios neurobiológicos de la función cerebral guiarán el futuro (Guillén, 2015).
El funcionamiento de los canales iónicos que activan las neuronas se predijo, por Hodgkin y Huxley, mediante un modelo matemático que consistía en un sistema de cuatro ecuaciones diferenciales no lineales; y todavía no se conocía la estructura de esos canales ni se habían podido observar directamente. La dificultad que tiene la creación de modelos matemáticos reside en la imposibilidad
de observar directamente las variables intrínsecas de las células vivas. Parece ser que esto está resuelto. Recientemente el matemático Iván Tyukin, de la Universidad de Leicester, en el Reino Unido, apoyándose en la física cuántica y registrando la actividad eléctrica de respuesta de estas células, ha creado un método que permite reconstruir las variables ocultas. Esta nueva técnica genera modelos matemáticos que describen el comportamiento de las células nerviosas del cerebro. Respecto al ?acoplamiento? por resurgimiento, podríamos expresarlo por el simple reconocimiento de propiedades o formulaciones matemáticas en otras realidades. Miguel Maravall, físico español, ha observado cómo las neuronas del sistema táctil de las ratas hacen cálculos estadísticos para adaptarse al entorno. El modelo de Teuvo Kohonen sobre las conductas asociativas de las neuronas para la información visual, descrito en 1982, se verificó en el año 2005. La Neurología ha tardado 23 años en demostrar que las ecuaciones del matemático se cumplen y que el comportamiento de esas neuronas se corresponde con la descripción matemática. Cuando Euclides divide un segmento de tal forma que AC + CB = AB, y, AC > CB, llama ?media
y extrema razón? a la proporción AB/AC = AC/CB. Esta proporción se conoce como el número Phi, y está presente en muchísimas realidades físicas: la disposición de los pétalos de una rosa, las conchas espirales de los moluscos, la disposición del cuerpo humano. Lo más desconcertarte es que, cuando nuestro cerebro considera algo armónico y bello, esta proporción está presente.
¿Es posible que nuestra estructura del cerebro ya tenga un conocimiento y una determinada configuración para la interacción con el medio, que nos haga entender el mundo así y no de otra manera?
¿Por qué consideramos que unas determinadas formas son bellas y otras no?
¿Por qué una realidad produce el mismo placer o disgusto en distintas y múltiples personas?
¿Por qué personas tan distanciadas y sin haber tenido nunca contacto cultural llegan a los mismos hallazgos?
¿Es necesario, respecto a nuestra forma de conocer, pasar por determinados procesos para la adquisición de determinados conceptos?
¿Es posible que, del mismo modo que hay transmisión genética de algunos conocimientos, haya transmisión genética de habilidades, facultades y estructuras que el cerebro humano ha ido desarrollando por los diferentes aprendizajes?
¿Podríamos decir entonces que hay transmisión genética de posibilidades de superación?
Asimismo, más importancia tiene el esfuerzo intelectual que el cerebro ha generado en el proceso de la adquisición que el resultado del aprendizaje. Y, si así fuera: ¿qué esfuerzos intelectuales convendría provocar para producir procesos que permitan el desarrollo del cerebro?; ¿qué esfuerzos se podrían considerar superiores y cuáles, básicamente, necesarios para que el cerebro humano mantenga las facultades intelectuales? Estas preguntas de exagerada importancia para la relación entre neurociencias y matemáticas tienen, a mi juicio, extrema y más importancia en consideraciones educativas y pedagógicas.
Ballestra, Martínez y Argibay (2006) nos revelan que, en un estudio realizado con bebés de 5 meses de edad, ?se colocó una marioneta en un escenario y luego se la cubrió con un telón. A continuación, otra marioneta idéntica a la primera fue ubicada delante del telón mientras el bebé observaba. Si al abrir el telón aparecían ambas marionetas, el bebé no se sorprendía, y no observaba durante mucho tiempo el escenario. En cambio, si la marioneta oculta por el telón se había retirado el bebé miraba al escenario durante un tiempo más largo. Lo mismo ocurría cuando aparecían tres marionetas. Estas respuestas indican que el bebé puede interpretar que el agregado de uno a uno da dos y no tres ni uno?.
En el Laboratorio de Estudios del Desarrollo de la Universidad de Harvard, se observó que los niños de 6 meses de edad pueden discriminar visualmente entre cantidades presentadas como cocientes de 2, tales como entre 16 y 8. Lo mismo sucede al percibir las cantidades en forma auditiva, lo cual avala la noción de que los bebés son capaces de procesar las cantidades en forma abstracta independientemente del modo de presentación, sea este visual o auditivo (Fei y Spelke, 2000). El conocimiento de los avances neurocientíficos aportará mucho a las consideraciones pedagógicas en los procesos de enseñanza-aprendizaje para el desarrollo de la actividad neuronal. Para saber cómo se enseña hay que saber cómo se aprende. Sin embargo, queda mucho que investigar para saber cuándo una respuesta determinada del cerebro se debe a condicionantes de métodos de enseñanza y cómo formas de enseñar diferentes pueden producir mayor o menor desarrollo de la actividad neuronal. Investigadores suecos demostraron recientemente que un entrenamiento de la memoria provoca cambios químicos en el cerebro humano. Esto prueba la relación interactiva que existe entre la cognición y la estructura del cerebro ( Radford y André, 2009). ?Parece imposible que nuestros genes determinen la estructura exacta de nuestros cerebros; mucho más verosímil resulta que éstos determinen modelos de crecimiento más o menos expuestos a los efectos modificantes de la experiencia? (Arbid, 1982), señala sobre el aprendizaje, para la enseñanza información recibida e información registrada. El cerebro humano recibe unos 400 mil millones de bits de información por segundo, pero solo somos conscientes 200 millones. De esa información registrada conscientemente, la memoria guarda aproximadamente un 10 %. En el mejor de los casos, de extrema atención, cuando nos dedicamos a exponer una lección, la memoria a corto plazo retiene el 10 % de la información registrada por el cerebro consciente. Si a esto añadimos que la exposición informativa de un tema exige habitualmente que el alumno se limite tan solo a escuchar, lo que se provoca es una pasiva actividad cerebral; y, dado que los estímulos del cerebro son bajos, suele inhibirse la motivación y variables afectivo-sociales, inhibiéndose también las respuestas de acción y reacción mental.
Diferente fijación cerebral se observa cuando presentamos propuestas desafiantes de obligado esfuerzo intelectual, o generamos diálogos abiertos a la búsqueda de conocimiento mediante intervenciones que permiten al aprendizaje el protagonismo que necesita. En estas situaciones no es la información, sino la formulación de preguntas la que reina de modo supremo. La actividad cerebral aumenta, y aumenta la cantidad de respuestas que se despliegan ante los estímulos percibidos. Se activan las atribuciones, la motivación, la reflexión, la autoestima. El cerebro consciente registra mucha más información, se mejora la memoria de trabajo y se retiene durante más tiempo. Las terminaciones nerviosas que tenemos en las yemas de los dedos estimulan nuestro cerebro. La manipulación de materiales genera una actividad cerebral que facilita la comprensión. Cuando se entiende y comprende lo que se está aprendiendo, se activan varias áreas cerebrales, mientras que cuando se memoriza sin sentido, la actividad neuronal es mucho más pobre. También, las características de los materiales didácticos y la metodología empleada en su utilización deberían ser objeto de investigación. Mediante un estudio computacional, se ha observado que la activación neuronal para el reconocimiento de cantidades es mayor si se estimula a partir de materiales didácticos.
Las matemáticas aprendidas desde la visión del neuroaprendizaje. Sentido numérico innato
Wynn (2015) demuestra, en sus estudios, que los seres humanos disponemos de un sentido numérico innato. Los bebés pueden distinguir operaciones con dos o tres objetos; es por tanto una capacidad con un componente genético. Se ha demostrado que nacemos con un concepto matemático numérico rudimentario que se limita a los números naturales iniciales (como máximo hasta el 4), esto quiere decir que ya en el primer año de vida los bebés son capaces de discriminar entre dos o tres objetos (este proceso se conoce con el nombre de subtizing).
2. Etapas del aprendizaje matemático (re-visitando Piaget).
Debemos aprovechar el sentido numérico innato para desarrollar un conocimiento matemático más complejo. Este conocimiento inicial podríamos equipararlo a la importancia de trabajar conciencia fonológica para el proceso de lecto-escritura.
Sousa (2008) identifica cinco niveles de comprensión del sentido numérico, que permiten al niño ir mejorando el conocimiento matemático.
Etapa 1. El niño no ha desarrollado el sentido numérico más allá de sus conocimientos innatos, por tanto, muestra
dificultades en entender las comparaciones entre cantidades y los términos del tipo más que/menos que o mayor/menor.
Etapa 2. Empieza a adquirir el sentido numérico que le permitirá entender conceptos como muchos, tres; pero no conceptos como más que o menos que.
Etapa 3. Comprende plenamente el significado de conceptos como más que o menos que y puede utilizar sus dedos para contar de uno en uno. Puede equivocarse en tareas en las que aparezcan números más que cinco.
Etapa 4. Puede contar sin necesidad de usar sus dedos; y empieza a entender la realidad conceptual de los números.
Etapa 5. Es capaz de recordar estrategias para resolver problemas porque empieza a automatizar operaciones aritméticas de las sumas; y comienza a entender conceptos básicos de las restas.
3. Factores esenciales para la enseñanza de las matemáticas
A partir de lo expuesto, podemos establecer algunos factores esenciales para la enseñanza de la aritmética desde la perspectiva neurológica:
Nuestro cerebro prefiere lo concreto a lo abstracto. Es necesario entender primero el sentido numérico no simbólico.
Nuestro cerebro aprende mediante la predicción y asociación con patrones de este modo podemos introducir conceptos matemáticos a la vida de los niños para que practiquen estimaciones y predicciones.
Nuestro cerebro se satura cuando utiliza muchos datos en la memoria de trabajo. Es imprescindible automatizar operaciones aritméticas, para no dedicar todos los recursos al cálculo y poder así dedicar parte de los recursos al análisis y razonamiento de los problemas.
Nuestro cerebro procesa los números utilizando tres procedimientos (visual, verbal y cuantitativo) en los que se activan regiones cerebrales distintas. Debemos activarlos todos mediante actividades con un enfoque multisensorial.
Nuestro cerebro es extraordinariamente plástico y modifica su forma
en función de la experiencia. Cualquier niño pue de mejorar su desempeño, incluso aquellos que padecen discalculia.
El aprendizaje es un proceso esencial que potencia nuestro desarrollo y nos permite adquirir destrezas, saberes, habilidades y competencias que nos facilitan desenvolvernos con éxito a nivel académico y profesional, pero también a nivel social y personal. A menudo nos hemos interesado por el aprendizaje, pero este interés es inútil si no centramos la visión en los sustratos biológicos del aprendizaje.
¿Qué ocurre en la mente de una persona cuando aprende? Entender esto nos ayuda a entender el aprendizaje y a poder gestionarlo de manera adecuada.
La educación ha de valerse de estos conocimientos básicos para que el educador disponga de las herramientas necesarias para desempeñar su labor.
Conocer cómo funciona la mente cuando aprende es muy importante para promover aprendizajes de calidad. Conocer las condiciones biológicas que son necesarias para el aprendizaje, y que lo potencien, nos hace posible potenciar el proceso.
Aportaciones del neuroaprendizaje y la neuroeducación
Las investigaciones sobre el funcionamiento de la mente en los procesos de aprendizaje nos demuestran lo siguiente:
El aprendizaje va acompañado, primero, de una maduración de las estructuras mentales que lo sustentan. Por eso debemos respetar los ritmos de desarrollo.
El aprendizaje consiste en el establecimiento de redes
neuronales. Para que se produzca un aprendizaje tenemos que crear la red pertinente. La manera de crear esa red es utilizando el mismo camino hasta asentarlo. Para ello debemos relacionar contenidos, reforzar conocimientos, llegar a las mismas conclusiones (usando los mismos caminos neuronales), utilizando diferentes alternativas de pensamiento.
Las emociones positivas potencian el aprendizaje y la motivación. Cuando una persona tiene emociones positivas relacionadas con algo que hace, tenderá a repetir eso para tener de nuevo las sensaciones positivas.
Para que se produzca el aprendizaje, es fundamental que estén cubiertas otras necesidades básicas. Si un niño, o una niña, tiene hambre o sueño, o tiene un problema con otros niños o niñas, tendrá más dificultades para aprender, ya que su mente, sus pensamientos, irán destinados a satisfacer esas necesidades o dificultades previas.
Para aprender, tienen que querer aprender. Para que la mente aprenda, hace falta cierta voluntad hacia esa tarea mental. Y para ello debemos despertar su interés, su curiosidad y sus ganas de aprender.
Conclusiones finales
Los nuevos tiempos requieren nuevas estrategias; y los últimos descubrimientos que nos aporta la neurociencia cognitiva desvelan que la educación actual requiere una profunda reestructuración, que no le impida quedarse desfasada ante la reciente avalancha tecnológica. Aunque hemos de asumir que la educación no se restringe al entorno escolar, la escuela y los docentes hemos de preparar a los futuros ciudadanos de un mundo cambiante. Para ello, hemos de erradicar la enseñanza centrada en la transmisión de una serie de conceptos abstractos y descontextualizados que no tienen ninguna aplicación práctica. Nuestros alumnos han de aprender a aprender y la escuela ha de facilitar la adquisición de una serie de habilidades útiles que permitan resolver los problemas que nos plantee la vida cotidiana: un aprendizaje para la vida. Y para ello se requiere inteligencia principalmente socioemocional.
El aprendizaje se optimiza cuando el alumno es un protagonista activo en aquel, es decir, se aprende actuando. Y esto se facilita cuando es una actividad placentera y se da en un clima emocional positivo. Nuestro cerebro nos permite mejorar y aprender a ser creativos; y es por todo ello que la neuroeducación resulta imprescindible.
Referencias
Agulló Morera, M.J., Filella Guiu, G., García Navarro, E., López Cassà, E., & Bisquerra Alzina, R. (2010). La educación emocional en la práctica. Barcelona, España: Horsori-ICE.
Alcazar, E. (2002). ?Hablando de mente y cerebro. Psiquiatría, neurociencia y psicoanálisis: convergencia e integración?. Vita: Academia Biomédica Digital.
Alonso, D., Fuentes, L. (2001). Mecanismos cerebrales del pensamiento matemático?. Revista de Neurología. Recuperado de https://pdfs.semanticscholar.org/6624/0f8c6778864ac6f8fa082012d58e7072dbb3.pdf
Ballestra, M., Martínez, J. & Argibay, P. (2006). ?Matemáticas y cerebro?. Revista del Hospital Italiano de Buenos Aires, (26) 1-123.
Bastos, A.A., González Boto, R., Molinero González, O., & Salguero del Valle, A. (2005). ?Obesidad, nutrición y actividad física?. Revista internacional de medicina y ciencias de la actividad física y el deporte, 5(18), pp. 140-153.
Blakemore, S.J., & Frith, U. (2011). Cómo aprende el cerebro: las claves para la educación. Barcelona: Ariel.
Butterworth, B. (1999). The Mathematical Brain. Macmillan. Corte, E.D., Greer, B., & Verschaffel, L. (1996). Mathematics teaching and learning. New York. Macmillan-NCTM.
Corte, E.D., Greer, B., & Verschaffel, L. (1996). Mathematics teaching and learning. New York. Macmillan-NCTM.
Dehaene, S. (1997). The number sense: How the mind creates mathematics. Oxford University Press.
Dehaene, S., Piazza, M., Pinel, P., & Cohen, L. (2003). ?Three parietal circuits for number processing?. Cognitive neuropsychology.
Dehaene, S., Spelke, E., Pinel, P., Stanescu, R., & Tsivkin, S. (1999). ?Sources of mathematical thinking: behavioral and brain-imaging evidence?. Science, 284.
Fei, X., & Spelke, E.S. (2000). ?Large number discrimination in 6-month-old infants?. Cognition 74, 1-11.
Fernández Bravo, J.A. (2010). ?Neurociencia y enseñanza de la matemática?. Revista Iberoamericana de Educación, (3), 78-98.
Gallese, V., Lakoff, G. (2005). ?The brain?s concepts: the role of the sensory-motor system in conceptual knowledge?. Cognitive neuropsychology. p. 22.
Radford, L., & André, M. (2009). ?Cerebro, cognición y matemáticas?. Revista Latinoamericana de investigación en matemática educativa, 12(2).
Wynn, K. (2015). ?Addition and subtraction by human infants?. Nature. 358, pp. 749-750.
Enlace alternativo

