1. Introducción

Todo código computacional necesita ser validado antes de ser implementado. La validación de un código computacional consiste en la comparación de los resultados numéricos contra una solución analítica o datos experimentales. Dada la complejidad de las ecuaciones diferenciales que describen el flujo incompresible, existen muy pocos casos de estudio que cuentan con soluciones analíticas. Estas soluciones sólo se pueden encontrar para flujos en régimen laminar con geometrías muy sencillas como placas paralelas, tuberías circulares, anillos o ductos rectangulares entre otros (Munson et al., 2006).

El perfil de velocidad para un flujo incompresible laminar completamente desarrollado dentro de un ducto rectangular se describe con ecuaciones hiperbólicas, las cuales fueron deducidas en base a la teoría de la elasticidad (Shah & London, 1978):

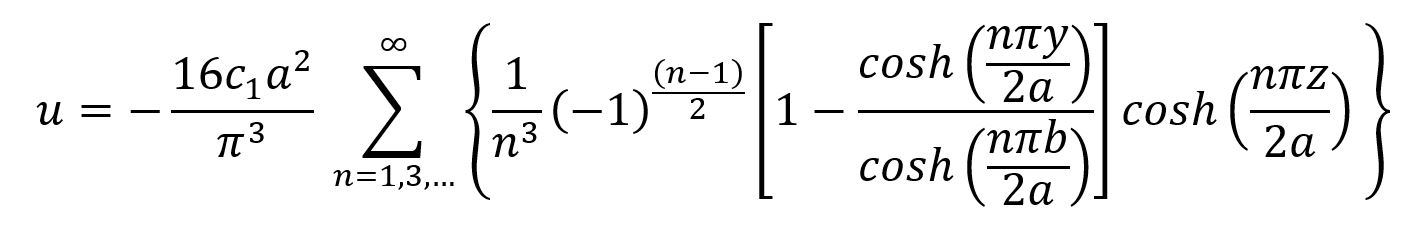(1a)

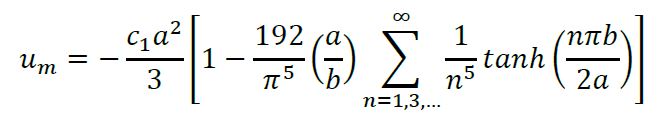(1b)

En dónde 𝑢 es el componente del vector de velocidad en la dirección de flujo (en la dirección 𝑥) en m/s cuando el flujo está completamente desarrollado, 𝑢𝑚 es la velocidad promedio de flujo en el eje en m/s, 𝑦 e 𝑧 son las coordenadas en el plano perpendicular a la dirección principal del flujo que describen la distancia en m desde el origen (centro del ducto) hasta el punto donde se está calculando 𝑢, 𝑎 es la mitad del ancho y 𝑏 es la mitad del alto del ducto, respectivamente en m, y 𝑐₁ es un parámetro que agrupa el gradiente de presión y las propiedades del fluido en m^-1s^-1.

Para ductos rectangulares con razón de aspecto de alto a ancho (α^∗=2𝑏/2𝑎) menor que 0.5, Purday (1949) desarrolló una ecuación aproximada que describe la relación entre 𝑢 y 𝑢𝑚 cuando el flujo está completamente desarrollado:

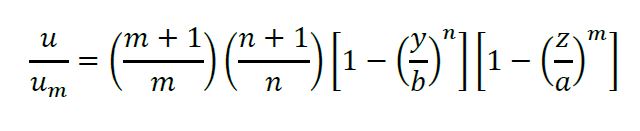(2)

En dónde 𝑛 = 2 y 𝑚 varía según la razón de aspecto del ducto (Tabla 1).

Tabla 1. Parámetro para ductos rectangulares con (adaptado de Shah & London, 1978).

Tabla 1

Parámetro para ductos rectangulares con α^∗≤0.5.

(adaptado de Shah & London, 1978)

A medida que la razón de aspecto (𝛼∗) del ducto rectangular tiende a cero, es decir a medida que el ancho del ducto se vuelve mucho mayor a su altura (𝑎≫𝑏), el comportamiento del perfil de velocidad cuando el flujo está completamente desarrollado tiende al descrito por las ecuaciones de flujo entre placas paralelas (Shah & London, 1978):

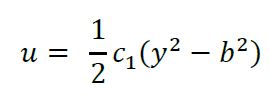(3a)

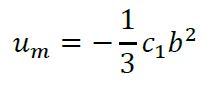(3b)

SimpleFoam es un solucionador de OpenFOAM para flujo incompresible laminar o turbulento en estado estable, el cual resuelve la forma diferencial de las ecuaciones de conservación de momento lineal (4) y de conservación de masa (5) utilizando el algoritmo SIMPLE (OpenCFD, 2018a; Patankar & Spalding, 1972). Este algoritmo permite calcular los campos de presión y velocidad en un volumen de control con flujo en estado estable mediante la introducción de un factor de corrección con el cual se asegura que el campo de velocidades obtenido de la ecuación de conservación de momento (4) cumpla con la ecuación de conservación de masa o de continuidad (5).

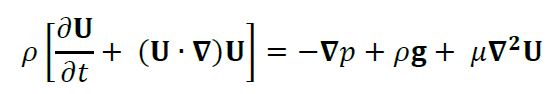(4)

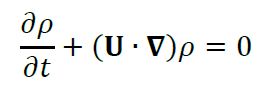(5)

Dónde, 𝐔 es el vector de velocidad, 𝑝 es la presión, 𝜌 y 𝜇 son la densidad y la viscosidad del fluido, respectivamente, 𝐠 representa el vector de aceleración de la gravedad y 𝑡 es el tiempo.

Para flujo estable e incompresible, la ecuación de continuidad (5) se reduce a la divergencia de la velocidad igual cero (7), y reemplazando esta ecuación en Navier-Stokes (4), y agrupando las fuerzas externas en un término fuente, se obtiene la forma de la ecuación de la conservación de momento que resuelve simpleFoam (6).

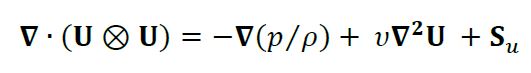(6)

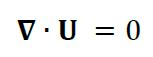(7)

Dónde, 𝜐 es la viscosidad cinemática, y 𝐒_𝑢 es el término fuente del momento.

SimpleFoam ha sido validado ampliamente para casos de estudio que van desde ejemplos clásicos en la dinámica computacional de fluidos como el perfil aerodinámico NACA0012 (Ashton & Skaperdas, 2019; Erney, 2008; Jiang et al., 2015) y el flujo en un ducto con salto en retroceso (Al-Jelawy et al., 2017; Inok et al., 2014; Robertson et al., 2015), hasta casos de estudio más complejos como el comportamiento aerodinámico de automóviles (Liets et al., 2017; Millewa et al., 2015) y ventilación urbana (Franke et al., 2012; Hong et al., 2017; Yu & Thé, 2016).

El objetivo de este trabajo es validar simpleFoam comparando los resultados de numéricos de una simulación de flujo laminar en un ducto rectangular con la solución analítica correspondiente. Además, se busca determinar el tamaño óptimo de malla para este y evaluar la razón de aspecto del ducto con la cual se puede asumir que el flujo dentro de este se comporta como flujo entre placas paralelas.

2. Metodología

2.1. Caso de Estudio

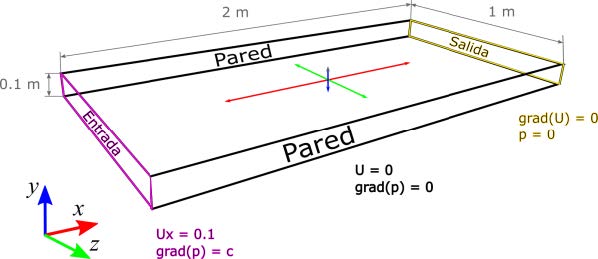
El caso de estudio seleccionado para la validación de simpleFoam consiste en la simulación del flujo de un fluido altamente viscoso e incompresible en régimen laminar dentro de un ducto rectangular de 1 metro de ancho por 2 metros de largo y 0.1 metros de altura (Figura 1). El fluido seleccionado para esta simulación es el aceite grado SAE 30, cuyas propiedades físicas a 15.6 ºC son las siguientes: Densidad (ρ) = 912 kg/m³, gravedad específica (γ) = 8.95 kN/m³, viscosidad absoluta (μ) = 0.38 N·s/m² y viscosidad cinemática (ν) = 0.00042 m²/s² (Munson et al., 2006).

Figura 1
Dimensiones del dominio computacional.

2.2. Modelación Numérica

El ducto se discretizó de manera uniforme utilizando celdas de 10 mm en las direcciones x e z, y celdas de 1 mm en la dirección y; lo que da como resultado 200, 100 y 100 celdas en las direcciones x, y e z, respectivamente, para un total de 2 millones de celdas. La discretización más fina en el eje y es necesaria para capturar la forma parabólica del perfil de velocidades en régimen laminar.

Para las condiciones de frontera, en la entrada se especificó un perfil de velocidad uniforme de 0.1 m/s, con lo que se obtuvo R_e = 43.3 para esta simulación. El gradiente de presión a la entrada del ducto se especificó como constante utilizando la condición fixedFluxPressure (OpenCFD, 2018b). Para las paredes se utilizó la condición de no deslizamiento para la velocidad y gradiente cero para la presión. A la salida del ducto se especificó gradiente cero para la velocidad y presión constante equivalente a la presión atmosférica (p = 0).

2.3. Validación y Enmallado Óptimo

Para la validación de simpleFoam los perfiles de velocidad simulados numéricamente se compararon con la solución analítica aproximada mostrada en la ecuación (2). Esta comparación se hizo a través del cálculo de un error normalizado (NRMSE) entre los valores simulados numéricamente y la solución analítica, dado por la siguiente ecuación:

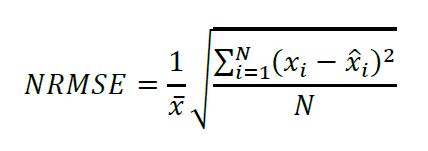(8)

Dónde, 𝑁 es el número de variables, 𝑥𝑖 y 𝑥̂𝑖 representan es el valor de la velocidad en el eje x dado por la solución analítica y numérica, respectivamente, y 𝑥̅ es el valor promedio de la velocidad en el eje x cuando el perfil de velocidad está completamente desarrollado.

El enmallado óptimo se estableció como el tamaño máximo de celda para el cual el error normalizado (NRMSE) de la solución numérica se encuentra por debajo del 1% con respecto a la solución analítica. El mismo se encontró variando el alto (dy) y luego el ancho (dz) de las celdas. El largo de las celdas (dx) no se modificó para este experimento.

Una vez encontrado el enmallado óptimo se procedió a aumentar el ancho del ducto rectangular para encontrar la razón de aspecto con la cual se puede asumir que el flujo dentro del ducto se comporta como flujo entre placas paralelas.

3. Resultados y Discusión

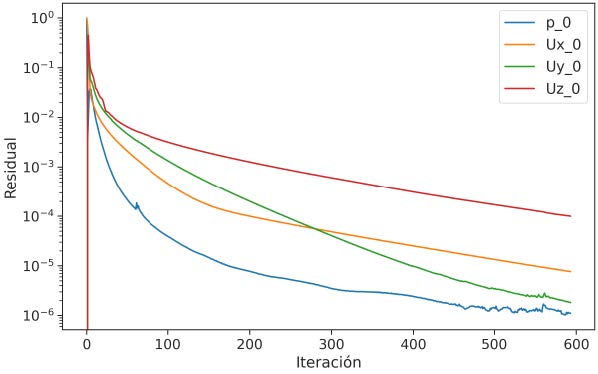
La solución numérica para el caso de estudio de flujo laminar en un ducto rectangular, con una discretización de 2 millones de celdas, convergió luego de 578 iteraciones del solucionador simpleFoam (Figura 2).

Figura 2
Residuales de la simulación de flujo laminar en un ducto rectangular con 2 millones de celdas con simpleFoam.

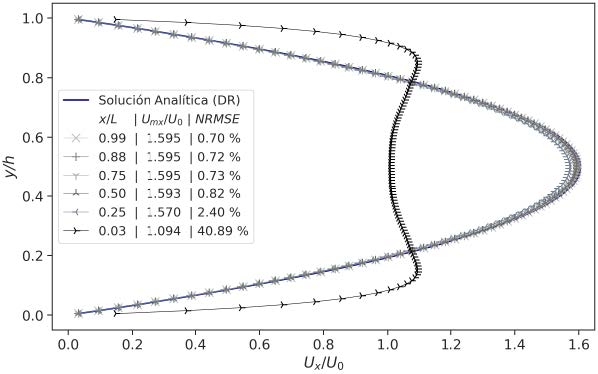
El perfil de velocidad completamente desarrollado simulado numéricamente utilizando simpleFoam se ajusta al perfil descrito por la solución analítica aproximada descrita para este caso (ecuación 2) con un error normalizado (NRMSE) a la salida del ducto (x/L = 0.99) del 0.70% (Figura 3). La proporción entre la velocidad máxima y la relación entre la velocidad máxima en el eje x (U_x) y la velocidad media o de entrada (U₀) cuando el perfil está completamente desarrollado es 1.6, lo cual concuerda con el valor teórico para un ducto rectangular con razón de aspecto (α) de 0.1 (McComas, 1967).

Figura 3
Perfiles de velocidad numéricos de flujo laminar (Re = 43.3) a lo largo del eje central (z = 0) de un ducto rectangular.

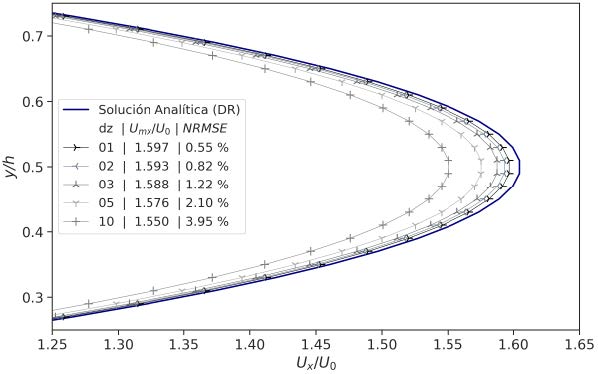
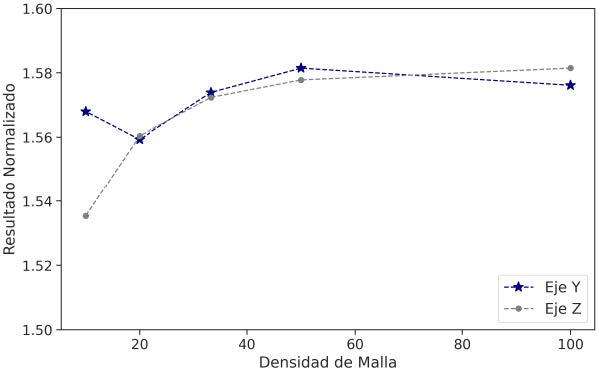
El enmallado óptimo, para el flujo laminar en el ducto rectangular se encontró con celdas de 2 mm y 20 mm en los ejes y e z, lo que corresponde a 50 celdas en cada eje, respectivamente (Figura 4). Utilizar una mayor densidad de malla en esos ejes no mejora significativamente el ajuste de los resultados numéricos a la solución analítica, ya que los mismos se pueden considerar independientes de la malla a partir de ese punto (Figura 5).

Figura 4
Perfiles de velocidad numéricos de flujo laminar (Re = 43.3) a la salida del ducto rectangular (x/L = 0.99) con dy = 2 mm, dx = 10 mm y diferentes anchos de celda (dz) en cm.

Figura 5
Análisis de independencia de la malla en dónde el resultado normalizado es Ux/Uo y la densidad de la malla se refiere al número de celdas en cada uno de esos ejes.

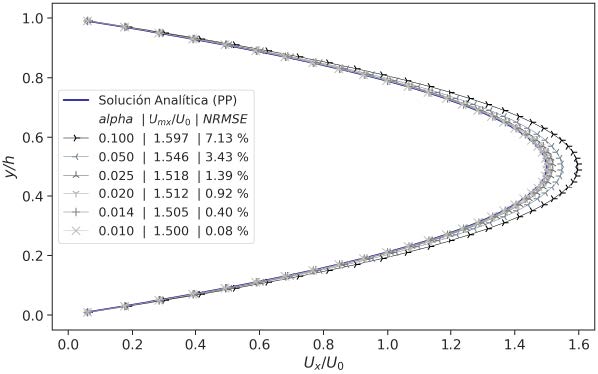
Finalmente, tomando en cuenta el límite del NRMSE como el 1%, se observa que la solución numérica de la velocidad de flujo laminar en el eje central de un ducto rectangular tiende a la solución analítica de flujo entre placas paralelas para ductos rectangulares con α < 0.02 (Figura 6).

Figura 6
Perfiles de velocidad numéricos de flujo laminar (Re = 43.3) a la salida del ducto rectangular (x/L = 0.99) con dx = 10 mm, dy = 2 mm y dz = 10 mm, para diferentes valores de alpha.

4. Conclusiones

La aplicación simpleFoam fue validada exitosamente para el caso de estudio de flujo laminar en un ducto rectangular. El error normalizado de la simulación numérica fue de 1% con respecto a la solución analítica. El tamaño óptimo de las celdas para este caso de estudio fue de 2 mm de alto por 20 mm de ancho. El largo de las celdas no se modificó para estas simulaciones y se mantuvo en 10 mm. Por último, se encontró que para ductos rectangulares con razón de aspecto (α) menor a 0.02 el perfil de velocidad completamente desarrollado en el eje central del ducto se puede representar utilizando la solución analítica para flujo entre placas paralelas.

Agradecimientos

Le agradecemos a la Secretaría Nacional de Ciencia, Tecnología e Innovación de Panamá (SENACYT) por proveer financiación para este trabajo a través del Proyecto IOMA19-006.

Referencias

Al-Jelawy, H., Kaczmarczyk, S., Alkhafaji, D., Mirhadizadeh, S., Lewis, R., & Cross, M. (2017). A Computational Investigation of a Turbulent Flow over a Backward Facing Step with OpenFOAM. Proceedings - 2016 9th International Conference on Developments in ESystems Engineering, DeSE 2016, 301–307. https://doi.org/10.1109/DeSE.2016.47

Ashton, N., & Skaperdas, V. (2019). Verification and Validation of OpenFOAM for High-Lift Aircraft Flows. Journal of Aircraft, 56(4), 1641–1657. https://doi.org/10.2514/1.C034918

Erney, R. W. (2008). Verification and Validation of Single Phase and Cavitating Flows Using an Open Source CFD Tool. Pennsylvania State University.

Franke, J., Sturm, M., & Kalmbach, C. (2012). Validation of OpenFOAM 1.6.x with the German VDI guideline for obstacle resolving micro-scale models. Journal of Wind Engineering and Industrial Aerodynamics Journal, 104–106, 350–359. https://doi.org/10.1016/j.jweia.2012.02.021

Hong, S.-W., Exadaktylos, V., Lee, I.-B., Amon, T., Youssef, A., Norton, T., & Berckmans, D. (2017). Validation of an open source CFD code to simulate natural ventilation for agricultural buildings. Computers and Electronics in Agriculture, 138, 80–91. https://doi.org/10.1016/j.compag.2017.03.022

Inok, F., Lavrov, A., & Guedes Soares, C. (2014). Analysis of complex fluid flow test cases with OpenFOAM. In C. Guedes Soares & F. Lopez Peña (Eds.), Developments in Maritime Transportation and Exploitation of Sea Resources. Taylor & Francis Group. https://www.researchgate.net/publication/263238693

Jiang, Y., Liu, C., Li, X., Liu, L., & Wang, H. (2015). Rainfall-runoff modeling, parameter estimation and sensitivity analysis in a semiarid catchment. Environmental Modelling and Software, 67, 72–88. https://doi.org/10.1016/j.envsoft.2015.01.008

Liets, R., Larson, L., Bachant, P., Goldstain, J., Silveira, R., Shademan, M., Ireland, P., Mooney, K., & Mooney, K. G. (2017). An Extensive Validation of an Open Source Based Solution for Automobile External Aerodynamics. https://doi.org/10.4271/2017-01-1524

McComas, S. T. (1967). Hydrodynamic entrance lengths for ducts of arbitrary cross section. ASME Journal of Basic Engineering, 89(4), 847–850. https://doi.org/10.1115/1.3609713

Millewa, U., Senathilaka, P., Dayarathna, W., Samarasingha, S., & Rangajeeva, S. (2015). Validation of OpenFOAM as Computational Fluid Dynamics (CFD) Software. Proceedings of 8th International Research Conference, KDU.

Munson, B. R., Young, D. F., & Okiishi, T. H. (2006). Fundamentals of Fluid Mechanics (5th Editio). John Wiley & Sons, Inc.

OpenCFD. (2018a). simpleFoam. https://www.openfoam.com/documentation/guides/latest/doc/guide-applications-solvers-incompressible-simpleFoam.html

OpenCFD. (2018b). Standard boundary conditions. https://www.openfoam.com/documentation/user-guide/standard-boundaryconditions.php

Patankar, S. V, & Spalding, D. B. (1972). A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. International Journal of Heat and Mass Transfer, 15(10), 1787–1806. https://doi.org/https://doi.org/10.1016/0017-9310(72)90054-3

Purday, H. F. P. (1949). Streamline Flow (First Edit). Constable and Co Limited.

Robertson, E., Choudhury, V., Bhushan, S., & Walters, D. K. (2015). Validation of OpenFOAM numerical methods and turbulence models for incompressible bluff body flows. Computers and Fluids, 123, 122–145. https://doi.org/10.1016/j.compfluid.2015.09.010

Shah, R. K., & London, A. L. (1978). Laminar Flow Forced Convection in Ducts: A Source Book for Compact Heat Exchanger Analytical Data. Elsevier Inc. https://doi.org/10.1016/C2013-0-06152-X

Yu, H., & Thé, J. (2016). Validation and optimization of SST k-u turbulence model for pollutant dispersion within a building array. Atmospheric Environment Journal, 145, 225–238. https://doi.org/10.1016/j.atmosenv.2016.09.043

Notas de autor

modelacion.matematica@udelistmo.edu