

A new perspective for the use of financial derivatives to hedge foreign exchange rate: L-BFGS perspective to assess the strikes and principals of plain vanilla options
Revista Activos, vol.. 17, no. 2, 2019
Universidad Santo Tomás


Artículos
Received: 29 May 2019
Accepted: 23 July 2019
Abstract: The international relationships between nations and economic agents have evolved so rapidly that the services and products are being traded almost instantly. Nevertheless, a great amount of these services and products are quoted in different currencies; thus, it is necessary the use of financial products to trade these products and services without incurring in unnecessary risks. The use of financial derivatives in the financial market has been increasing over the last decade. Moreover, foreign exchange derivatives have become an essential tool for companies to hedge their exposure in a foreign exchange currency. Nonetheless, there has not been enough research about methodologies that emphasize in the mixing of strategies. In this document, we develop a methodology to hedge effectively. Hence, we propose the Limited-memory bfgs in order to find the optimal percentage of the position of the derivative based on simulations created by a garch model. In this paper, we show an example with an exporting Colombian company based on Colombia, which has an exposure in us American Dollars. In this example, we find that the methodology proposed has a lower Value at Risk than a strategy using derivatives operating in isolation.
Keywords: Foreign Exchange risk, Foreign Exchange Hedge, Financial Derivatives, garch family, Limited-memory bfgs.
Resumen: Las relaciones internacionales entre las naciones y los agentes económicos han evolucionado tan rápidamente que los servicios y productos se comercializan casi instantáneamente. Sin embargo, gran parte de estos servicios y productos se cotizan en diferentes monedas; por lo tanto, es necesario el uso de productos financieros para comercializarlos sin incurrir en riesgos innecesarios. El uso de derivados financieros en el mercado financiero ha ido aumentando en la última década. Además, los derivados sobre divisas se han convertido en un instrumento esencial para que las empresas puedan cubrir su exposición en una moneda extranjera. No obstante, no se ha investigado lo suficiente sobre las metodologías que hacen hincapié en la mezcla de estrategias. En este documento, desarrollamos una metodología para cubrir eficazmente. Para esto proponemos el bfgs de memoria limitada con el fin de encontrar el porcentaje óptimo de la posición del derivado con base en simulaciones creadas por un modelo garch. En este documento, mostramos un ejemplo con una empresa exportadora colombiana con sede en Colombia, que tiene una exposición en dólares americanos. En este ejemplo, encontramos que la metodología propuesta tiene un menor valor en riesgo que una estrategia que utiliza derivados que operan de manera aislada.
Palabras clave: riesgo del tipo de cambio, cobertura del tipo de cambio, derivados financieros, familia garch, bfgs de memoria limitada.
Introduction
Nowadays, the globalization and the increasing commerce between nations have changed dramatically the way how a company is structured. First, firms have risen their efforts to search for supplies in foreign lands in order to find out more competitive prices. Second, corporations have been looking to ameliorate their profits by taking their products to foreign lands. Thus, these firms must trade with a foreign currency, in other words, they face a foreign exchange risk. A foreign exchange risk, also known as fx risk, occurs when a financial transaction is denominated in a currency different from the base currency. For instance, exporting firms have fx risk when the exchange rate decreases substantially because it will affect its profit.
In the financial market, it is vital to mitigate the fx risk with the purpose to reduce the variance of the exchange rate; thus, the financial sector has developed the foreign exchange derivatives. These financial tools help to avoid efficiently the systematic risk by transferring the risk to the individuals with more risk tolerance. At the present time, the most common derivatives in the fx market are the Forward, the Call, and the Put. These three derivatives are extensively used by firms to hedge their different exposures.
This paper introduces a methodology with the aim to optimize the use of the derivatives when a company is hedging fx risk. First, we use the garch model to estimate a certain amount of simulations for a certain exchange rate. Second, we valuate the foreign exchange exposition of the company by using the simulations. Finally, we use the Broyden-Fletcher-Goldfarb-Shanon (bfgs) algorithm to propose the optimal strike and unit of each derivative by taking in account the firm’s risk appetite. For example, if the exposition is 1000 usd (United States Dollars) and the company is located in Colombia; we start by simulating the usd/cop exchange rate a certain number of times and then we multiply each output of the simulation times the exposition (1000 usd). Then, we evaluate which derivative could be used to hedge; in this example, ForwardS and CallS are the best options. To finish, we use the l-bfgs algorithm to estimate the optimal strike and principal for the Forwards and Calls.
This paper is structured as follows. The first section corresponds to this introduction; the second section considers the theoretical framework of this paper; the third section presents the methodology proposed; the fourth section presents an example with an exporting Colombian company; and the fifth section shows the conclusions.
Theoretical Framework
Foreign Exchange Risk
Globalization and the increasing commerce between nations have changed dramatically the way how a company is structured (Graham & Harvey,2001). First, firms have risen their efforts to search for supplies in foreign lands in order to find more competitive prices. Second, corporations have been looking to ameliorate their profits by taking their products to foreign lands. Thus, these companies must trade with a foreign currency, in other words, they face a foreign exchange risk.
Levi (2009, p.310) introduces the concept of operating exposure as the implications of exchange rates for the revenues, costs, and profitability of companies directly or indirectly involved in international commerce. Levi (2009, pp. 318-320) exemplifies this exposure by describing the effects of exchange rates on an exporter’s product price, which affect cash outflows. Bodnar & Bartam (2007) cite that anecdotal evidence from business press suggests that unexpected exchange rates affect the value of corporations with foreign-currency based activities, assets, and/or competition.
Notwithstanding, operating exposure is not just related with international corporations. Levi (2009, p. 310) points out that some firms face operating exposure without ever dealing in foreign exchange. The example given is with the loss of foreign tourist due to a change in the exchange rate. Bartam (2007) estimated the foreign exchange rate exposure of numerous nonfinancial firms and found that a great percentage of them have exposure to at least one foreign exchange rate.
Henceforth, every sector in the global economy is exposed to operating exposure. Our objective in this research is to estimate and reduce the exposure to foreign exchange risk. This challenge might be faced with the use of fx (foreign exchange) derivatives such as forward contracts, futures contracts options, and swaps.
FX derivatives
Hull (2009, p. 1) defines a derivative as a financial instrument whose value depends on the value of other, more basic underlying. Moreover, a fx derivative is a financial derivative whose payoff depends on the foreign exchange of two (o more) currencies.
The principal purpose for the existence of derivatives is because of the uncertainty about the future rates of exchange. fx derivatives can allow investors and corporations to transfer risk, but also earn some profit through speculation. Geczy et al. (1997) examines the use of fx derivatives to test the different theories of hedging behavior. He found that larger firms are more likely to use fx derivatives in order to reduce the cash flow variation. Jewitt (2015) describes extensively the correct use of fx derivatives with the aim to hedge.
Currently, the use of financial derivatives has been increasing dramatically. According to the bis (Bank for International Settlements) data, the amount of operations with derivatives increased 83% in the period between June 1998 to June 2009, reaching a value of $605 usd billion.
Even though we propose a methodology to hedge efficiently using fx derivatives, in this first investigation we are just going to use plain vanilla options such as forward and the two well-known options European call and European put. The following definitions were obtained in Hull (2009).
• Forward: forward commitments are contracts entered at one point in time that require both parties to engage in a transaction at a later point in time (the expiration) on terms agreed upon at the start. The parties establish the identity and quantity of the underlying, the way the contract will be executed or settled when it expires, and the fixed price at which the underlying will be exchanged. This fixed price is known as forward price.
• Option: an option is a derivative contract in which one party, the buyer, pays a sum of money to the other party, the seller or writer, and receives the right to either buy or sell an underlying asset at a fixed price on a specific expiration.
‐ Call: the buyer has the right to buy.
‐ Put: the buyer has the right to sell.
Nevertheless, the use of fx derivatives must be well used, or they will have a fatal impact on the P&L (Profit and Loss) of the sector. For example, a company resides in Colombia and it exports products to United States; hence, this company has an exportation exposure in United States dollars because its incomes are in American dollars and its costs are in Colombian pesos. One day, this company decides to hedge its exposure of the next month using a forward contract with a forward price of $3150 cop = $1 usd. Nonetheless 30 days after, the spot price is $3200 cop = $1 usd. Thus, this Colombian company losses $50 cop for every $1 usd received from its products sold in United States. Furthermore, this case exemplifies the risk for the P&L of using incorrectly fx derivatives.
Strategies with derivatives
Jewitt (2015, pp.121-136) affirms that vanilla derivatives can be combined to create different payoffs. Some of these combinations are so well known that the strategies have already been named. For an fx derivative trader, the most important is to understand how these strategies impact the exposures in the trading position. Some research has focused on understanding these positions. Mullaney (2011) describes in detail a variety of option strategies, from the riskiest (selling to naked puts) to the more conservative using covered positions (Covered call). Chaput & Ederington (2003) examined large trades in Eurodollar and found that at least three-fourths of the trading consists of combinations. They also found that these combinations exist because they hedge specific risks such as volatility.
First, it is essential to establish that a derivative can have a long or short position. A long position in a derivative means that you own the asset. Speculators often keep a long position when their expectations for the price of the financial asset is to rise. In the case of an option, the long position is the one who pays the sum of money and it has the right to buy or sell the underlying asset. On the other hand, the short position in a derivative means that you do not own the asset. Investors usually take a short position when their expectations for the price of the financial asset is to decline. In the case of an option, the short position is the one who receives the sum of money and the risk associated with the option. In this research, we attempt to establish an optimization methodology to choose wisely which position is the best option for the P&L of the sector.
Second, an exposure in a foreign exchange does not have to be hedged with just one derivative; moreover, it is convenient sometimes to hedge with more than two derivatives in order to ameliorate the impact to the exposures in the trading position. Hence, we attempt to estimate the optimal percentage of each type of derivative that the investor is going to use in his position.
GARCH Models
The garch family is a group of statistical models for time series used to model a change in the variance over time. This property in statistics is called heteroskedasticity. The name of the most basic model is arch (Autoregressive Conditional Heteroskedasticity), which is a process introduced by Engle (1982). The arch explicitly recognizes the difference between the unconditional and the conditional variance allowing the latter to change over time as a function of past errors. Then, the garch (Generalized Autoregressive Conditional Heteroskedasticity) model, introduced by Bollerslev (1986), is an extension of the arch model that incorporates a moving average component. A third model is the garch-m created by Engle et al. (1987). This process allows the conditional mean of the time series to depend on its conditional variance. The egarch (Exponential Generalized Autoregressive Conditional heteroskedastic) model by Nelson (1991) is our fourth model. In this model, the variance does not behave in a symmetric way for positive and negative disturbances, as happens on the garch models. This feature is desirable because the prices of a financial asset tend to behave differently for ups and downs in the daily market. Finally, the fifth model is the gjr-garch, introduced by Glosten et al. (1993). In this model, the zero-mean white noise, despite of being serially uncorrelated, does not necessarily need to be serially independent. The gjr-garch assumes and estimates a specific, normally linear, parametric form for this conditional heteroskedasticity.
To sum up, we use the garch family (arhc, garch, garch-m. egarch and gjr-garch) to choose the most appropriate model using the aic criteria. Then, the model is estimated to create the simulation of the multiple paths that the exchange rate might have in the future.
bfgs algorithm
Numerical optimization is the core for many mathematical problems. Once the model is built and the function is defined, the problem focuses in minimizing a multivariate f (x), where x is in some high-dimensional space. In other words,
Then is which minimizes the function . In this research, we use a quasi-Newton method named Limited-memory bfgs (Broyden-Fletcher-Goldfarb- Shanno) to find the optimal combination of derivatives required to hedge effectively. First, this algorithm is used because it allows the incorporation of “box constrains” (multiple linear constraints). For example, if our desire is not to take a short position in a put more than once the exposure, this algorithm of optimization fits the desire perfectly. Second, the l-bfgs allows nonlinear functions, which it is mandatory for this research because the valuation of the derivatives is nonlinear. Third, the hessian matrix does not have to be calculated, and it is approximated by gradient evaluations, which decreases the complexity of the optimization algorithm and significantly reduces the time of computation.
Historical context of the derivatives market in Colombia
In 2001, the Colombian stock exchange was created by unifying the Bogota stock exchange, the Occidente stock exchange, and the Medellin stock exchange. The first was mainly created because of the opportunities of arbitrage presented in Colombia. In 2008, the standardized derivative market started because of the need of some sectors to hedge their exposure in foreign currency.
The financial market needed a very developed technological infrastructure, since it must allow transparency, speed, and security in the interaction of the participants of this market. In Colombia, at the beginnings of the 2000s, the stock exchange market did not have a sufficiently solid structure for this market in accordance with Cañas (2006). The negotiation of derivative instruments requires an infrastructure technology with specific conditions for this type of market, that even the country does not have, and it will be difficult to acquire it.
The derivatives market in Colombia is a market in its growth stage and consolidation since it is very recent. Implemented in 2008, the Stock Exchange of Colombia, within its new developments and products for the market, launched the futures on trm (Colombian Peso Market Exchange Rate), thus allowing the different participants to have the possibility of carrying out hedging, speculation, and arbitrage operations. The market of standardized derivatives has had a growth stage since its launch. In 2012, more than 600,000 contracts represented in volumes of more than 60 reached billions of pesos. For the year 2013, there was a growth where they were able to operate almost the 700,000 contracts represented in a volume of 83 billion pesos (Bernal Parra, 2018).
Mejía & Zabala (2010) created a survey to assess the characteristics of the derivative market in Colombia. This study was fed primarily from primary information collected from a survey designed for companies in the manufacturing industry. The applied survey corresponds to a design by professors Jaime Humberto Sierra and Julio Sarmiento based on the Wharton/Chase derivative survey (1995) and the utdt Wharton Weiss Center survey (2000).
Mejía & Zabala (2010) found that out of a total of 201 companies interviewed, 90 firms effectively use or have had the experience of using derivative products as Forwards, Options, Futures, or Swaps. This corresponds to 44.78% of the total the sample. Although at first glance you can think that the almost half is covering your risk, this percentage is low if we consider that absolutely all companies included in the study are exposed to some type of market risk; in addition, as we will see later, the companies that have performed these operations have been limited to a single instrument.
Methodology
In this section, we propose a step by step procedure in order to effectively choose the financial derivatives. This section is organized as follows:
• Identify the exposure
• Estimate the model
• Perform the simulations
• Perform the optimization
Identify the exposure
In the case of a company with foreign exchange risk, there are three possible cases. First, the company imports services and products, which are quoted in a different currency. Second, the company exports services and products, which are quoted in the local currency. Third, the company embodies the two previous cases.
For the first case, the company imports products and services, which are necessary for the operation of the company, but they have a selling price in a currency different from the local one. In this case, the company is affected by a high exchange risk because its inputs increase their level without its outputs being affected by the same event. The firm would be interested in the software if we could assure it a lower exchange rate than the open market.
The second case we study is about an exporting company. This firm benefits from an increase of the exchange risk since their utility might increase. Hence, the application would be useful if the average exchange rate the software will give is higher than the market’s one.
Finally, the last option is a firm which faces the two kind of exposures. Normally, this type of company pays its debts in a foreign currency and receives its utility using a different currency. For instance, a company based on Colombia, which imports from China using yuans and exports to United States of America using United States dollars.
The first step to use properly this software is to separate debts and credits by currency. This software is made to hedge just one currency at a time; hence, the software is going to be used as many times as many currencies the company faces. Second, the exposures should be spread by due dates. The firm ought to organize its flows by date and identify the quantity of days until the expiration of every exposure. Third, it is mandatory to net the outflows and inflows of the same due date. For example, if the firm has two debts of 5000 United States dollars and one credit of 12000 United States dollars by the 5th of July, then, the firm should report in the software that it has a credit of 2000 United States dollars by the 5th of July.
Once the report of credits and debts is organized in a spreadsheet following the indications given in this section, we can proceed to the next section of this chapter.
Estimate the model
In this section, the main task is to estimate the best model in order to forecast the exchange rate. For this assignment, it is necessary to have at least 2 years of history of the daily exchange rate in order to estimate the long-term effect, the cycles, and the seasonality.
First, we highly recommend using the exponential smoothing to determine the long-term effect. This method assigns exponentially decreasing weights over time. It also helps to ameliorate the heteroscedasticity of the time series, which tends to be very useful to estimate a linear time series.
Second, we suggest using the Fourier decomposition with the aim to explain the series entirely as a composition of sinusoidal functions. In the case of an exchange rate, if there are regular harmonic components in the process generating the data, we could estimate the proportion of the variance attributed to this movement.
Third, having omitted the long-term effect with the exponential smoothing and the seasonality with the Fourier decomposition, we could estimate a garch model. In this step, we estimate every model of the garch family and select the model with the best forecast ability. We assess the forecast ability by deleting the last periods of the time series and using the model to forecast the same last periods; then, we estimate the square mean error of every model and, finally, we select the model with the minimum square mean error.
Perform the simulations
Next, we use the model chosen to perform a vast quantity of simulations. In this step, we use the garch model to forecast the different paths that the exchange rate might follow. It is true that forecasting a financial time series is a tremendous, demanding, and difficult task; thus, we remind the reader of this paper this is not to make arbitrage in the financial market, rather we attempt to identify the best strategy to hedge efficiently the exposure to the fx rate. Consequently, we use the garch model chosen with normally distributed random variables to create simulations for the foreign exchange rate. The simulations must end the day of the maximum due date of the outflows and inflows recorded in the spreadsheet. It is important to remind the reader that the simulations have to be based on working days rather than calendar days because the exchange rate does not move neither on weekends nor on national holidays.
Perform the optimization
Finally, we attempt to optimize the use of derivatives to hedge effectively. First, let’s go over some definitions.
• Callt (k, m): is a call option with a strike of k and a principal of m, which can be positive if it is a long position and negative if it is a short position, with a due date of t.
• Putt (k, m): is a put option with a strike of k and a principal of m, which can be positive if it is a long position and negative if it is a short position, with a due date of t.
• Forwardt (m): is a forward with a principal of m, which can be positive if it is a long position and negative if it is a short position, with a due date of t. The forward strike is determined by the market and it is rarely customized.
In this step, we define a general function which has as an input of the strikes and the principals of the financial derivatives and the simulation. This function is named P&L (Profit and Loss) because it assesses the P&L of the company for a certain simulation and a certain combination of principals and strikes of the financial derivatives.
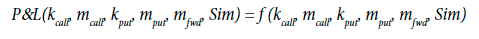
In the case where we use every simulation, we could define a P&L average (P&L), which estimates the average Profit and Loss of the use of certain combination of principals and strikes of the financial derivatives. Thus, our main objective is to find out the optimum combination of strikes and principals which maximizes the P&L.
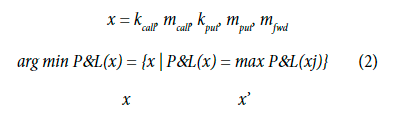
In this part of the document, we recommend using the l-bfgs algorithm to find out the optimal combination of strikes and principals to hedge effectively. As previous commented, this algorithm is chosen because it allows nonlinear optimization and it also does not require a significantly time of computation. Case of study: exporting Colombian company.
Conclusions
To sum up, we could not find a software, which assess the problem of using a mixture of financial derivatives. Hence, we propose this methodology to appraise the need of some sectors to effectively hedge their exposure to foreign exchange rate. Subsequently, we propose a statistical methodology to solve this problem. We found that the method proposed reduces significantly the fx risk because the P&L under the combination of strikes and principals estimated is significantly lower in variance than the P&L without using financial derivatives. These conclusions are based on the example shown with the exposure shown.
Moreover, we also found that using the method proposed with the exporting Colombian company, the P&L is less volatile than using just a straightforward strategy. This is true because the optimization proposed minimizes the VaR, which estimates how much a set of exposures might lose with a given likelihood, given normal financial market conditions, in a range of period, such as a day. Finally, we recommend testing additional methods of optimizations since the l-bfgs does not converge when the optimum is very distant.
References
Bartam, S. M. (2007). Corporate cash flow and stock price exposures to foreign exchange rate risk. Journal of Corporate Finance, 13, 981–994.
Bernal Parra, J. L. (2018). Características y evolución del mercado de derivados futuros sobre tasas de cambio en Colombia 2014–2016 (PhD thesis), Universidad de la Salle, Facultad de Ciencias Administrativas y Contables, Bogotá, Colombia.
Bodnar, G. M. & Bartam, S. M. (2007). The exchange rate exposure puzzle. Managerial Finance, 33, 642–666.
Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics, 31, 307–327.
Cañas, N. (2006). Perspectivas del mercado de derivados en colombia. Retraso derivado del desconocimiento. Ad-Minister, 9, 156–166.
Chaput, J. S. & Ederington, L. H. (2003). Option spread and combination trading. The Journal of Derivatives, 10, 70–88.
Engle, R. F. (1982). Autoregressive conditional heteroscedastiticy with estimates of the variance of united kingdom inflation. Econometrica, 50, 987–1008.
Engle, R. F., Lilien, D. M. & Robins, R. P. (1987). Estimating time varying risk premia in the term strucute: The arch-m model. Econometrica, 55, 391–407.
Geczy, C., Minton, B. & Schrand, C. (1997). Why firms use currency derivatives. The Journal of Finance, 52, 1323–1354.
Glosten, L. R., Jagannathan, R. & Runkle, D. E. (1993).On the relation between the expected value and the volatility of the nominal excess return on stocks. The Journal of Finance, 48, 1779–1801.
Graham, J. & Harvey, C. (2001). The theory and practice of corporate finance: Evidence from the field. Review of Financial Studies, 14, 215–241.
Hull, J. (2009). Options, Futures and Other Derivatives, Options, Futures and Other Derivatives. New Jersey: Pearson/Prentice Hall.
Jewitt, G. (2015). fx Derivatives Trader School. New Jersey: John Wiley Sons.
Levi, M. D. (2009). International Finance. London & New York: RoutledgeTaylor Francis.
Mejía, M. J. & Zabala, J. G. (2010). Uso de derivados para el cubrimiento de riesgo operativo y crediticio en empresas manufactureras en Colombia (PhD thesis). Pontificia Universidad Javeriana, Facultad de Ciencias Administrativas y Económicas, Bogotá, Colombia.
Mullaney, M. D. (2011). The Complete Guide to Option Strategies: Advanced and Basic Strategies on Stocks, etfs, Indexes, and Stock Index Futures. New Jersey: John Wiley Sons.
Nelson, B. D. (1991). Conditional heterocedasticity in asset returns: A new approach. Econometrica, 59, 347–370.
Notes

