

Whole-body SAR simulations on a prolate spheroid using different plane wave polarizations up to 100 GHz
Simulaciones de tasa de absorción específica (SAR) de cuerpo completo sobre un esferoide prolato utilizando diferentes polarizaciones de onda plana hasta 100 GHz
 http://orcid.org/0000-0003-4712-7490 José Enrique Hernández-Bonilla enrique.hernandez.bonilla@gmail.com.
http://orcid.org/0000-0003-4712-7490 José Enrique Hernández-Bonilla enrique.hernandez.bonilla@gmail.com.
Tecnología en marcha
Editorial Tecnológica de Costa Rica, Costa Rica
ISSN-e: 2215-3241
Periodicity: Trimestral
vol. 32, no. 4, 2019
Received: 23 January 2019
Accepted: 06 May 2019

Abstract: This exploratory paper discusses the simulation of the whole-body specific absorption rate (SAR) on electrically large bodies. By irradiating a spheroid by means of a plane wave, the relationship between the radiated electromagnetic fields and the internal fields generated in the object can be studied. The SAR could be calculated with conventional numerical methods up to 9 GHz with the computational power available. To overcome this limit, an approach using physical optics is proposed to extend the simulation range up to 100 GHz. Preliminary results obtained indicate that this could be a good alternative for high frequency simulations; however, the generalization of the method and further validation would be required as future work.
Keywords: Bio-Electromagnetism, Computational Electromagnetics, High-Frequency Fields, Physical Optics, Specific Absorption Rate.
Resumen: Este trabajo exploratorio discute la simulación de la tasa de absorción específica (SAR) de cuerpo completo sobre objetos eléctricamente grandes. Al irradiar un esferoide por medio de una onda plana se puede estudiar la relación entre los campos electromagnéticos irradiados y los campos internos generados en el objeto. Fue posible calcular el SAR de cuerpo completo a través de métodos numéricos convencionales hasta 9 GHz con la capacidad de procesamiento computacional disponible. Para superar ese límite, se propone un acercamiento por medio de óptica física con el cual se pudo extender el rango de las simulaciones hasta 100 GHz. Los resultados obtenidos indican que este puede ser un acercamiento adecuado para simulaciones en alta frecuencia, sin embargo, se requiere generalizar el método y validarlo de forma estricta como trabajo a futuro.
Palabras clave: Alta Frecuencia, Bioelectromagnetismo, Electromagnetismo Computacional, Óptica Física, Tasa de Absorción Específica .
Introduction
In recent years, with the advent of new technologies that work and communicate at higher frequencies, there is a need to understand more deeply the associated radiation effects on humans and living beings. Exhaustive research has been made for different applications and with different objectives, from complex 3D human models in e.g. [1]-[10], to simpler geometrical models in e.g. [11]-[16]. Most of them address the frequency range from 1 up to 6 GHz, with some studies below the GHz range [12]-[16]. However, a few works explore frequencies higher than 6 GHz [10]-[11], a range that is being used in diverse products and applications.
Computational tools to tackle electromagnetic problems are now more powerful thanks to code optimization and the availability of more processing power. This opens the possibility to study this frequency range with more detail than before; however, as the computational requirements increase with the maximum frequency of interest, the simulation of electrically large bodies remains challenging.
In this paper, results reported in [11] regarding plane-wave incidence with different polarizations on a spheroid are replicated with state-of-the-art numerical methods. The goal is to analyze the state of current tools and their ability to solve SAR computations at high frequencies when working with large bodies of a size representative of human beings. Since the available computational resources limited the analysis to a maximum frequency of 10 GHz, a method exploiting physical optics was also explored to extend the frequency range. Consistent results could be computed up to 100 GHz, although restricted for some specific configurations.
Whole-Body SAR on a prolate spheroid
For dynamic electromagnetic (EM) field simulations, various methods and tools can be used to obtain results of interest. Different numerical methods are available, which are suited to tackle different types of problems. In the scope of this paper, two methods were used to calculate the EM fields: The Finite Integration Technique (FIT), which discretizes Maxwell’s Equations in their integral form, and the Method of Moments (MoM), which transforms the integral form into a linear system that can be numerically solved.
The problem of interest is a classic scenario used in bioelectromagnetics, where a prolate spheroid is irradiated by a plane wave and the goal is to calculate the total power absorbed by this body. Three different wave polarizations are used to determine the differences in power absorption, as depicted in figure 1. The utilization of a prolate spheroid is representative of the behavior expected on a human body.
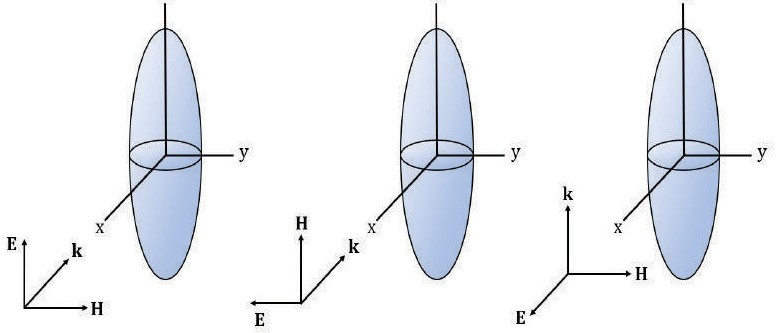
Each polarization will dictate a different behavior on the power absorption across the frequency spectrum. Four regions can be found based on the behavior of the power absorbed by the E polarization [14]. A sub-resonance region that goes up to 30 MHz exhibits an increase of the power by a factor of f2 for all three polarizations. Next, the resonance region is identified, which spans from 30 to 300 MHz. Even though, H and K polarizations also reach a peak resonance value, they are not as high as the one obtained by E polarization. This resonance can be compared to that of a wire antenna with the difference that resonance for a biological tissue reaches its peak when the object size (major axis) is about four-tenths of the external wavelength, whereas the antenna has it when its size is half the wavelength. These differences are due to the lossy dielectric material of biological tissues and the shape of the body. The resonance frequency depends on the size of the object. In the case of prolate spheroids, it is closely related to the ratio between the major and minor axis. If the dimensions are small, like the ones of a small child, the peak of the resonance is located at a higher frequency; if dimensions are larger, the peak shifts to a lower frequency [1]. After reaching this peak, the whole-body SAR decreases with a factor of, approximately, 1/f. The following region is called the “Hot-Spots” region; this is due to the absorption being localized in some areas. It spans from 300 MHz to 3 GHz. As seen in figure 2, the whole-body absorption decreases. The last region goes from 3 GHz onwards and it is called the surface absorption region because all the energy absorbed is mostly localized at the surface of the body [14].
At frequencies below resonance, the SAR for E polarization is the highest, for H polarization is the lowest, and for K polarization is located between the other two. This behavior is related to the average strengths of the internal fields; for example, the internal E field is stronger when the incident E field is mostly parallel to the major axis than when it is normal to the minor axis. Also, the internal E field generated from the incident H field is greater when the cross-sectional area intercepted is large [17].
To estimate the power absorbed from the body, the use of the specific absorption rate (SAR) is a good metric for obtaining the value of interest. Thanks to the nonmagnetic characteristics of biological tissues, power absorption depends greatly on the E field strength.
SAR is defined as transferred power divided by the mass of the object [18] and it can be represented in different ways. For a time-average, the formula is given by:
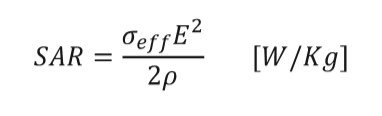 (1)
(1)Previous research [11] has shown that whole-body SAR behaves differently when plane waves are polarized in the three ways shown in figure 1. These different behaviors depend on EM field strengths, the body symmetry, and material selection.
Whole-Body SAR on a prolate spheroid using full-wave simulators
To replicate the behavior described in [11], two full-wave solvers were used; CST Microwave Studio which is a commercial tool that works in the time domain using the Finite Integration Technique (FIT) [19] and the Method of Moments (MoM)-based solver CONCEPT-II, which is an academic tool developed by the Institute of Electromagnetic Theory (TeT) of the Hamburg University of Technology (TUHH) [20]. The simulated body is a prolate spheroid with a major axis of 1.8 m and a minor axis of 0.3 m which resembles the dimensions of an adult human. The material chosen for the body is water modeled as a lossy dielectric. In order to work with a simpler geometric model, different dimensions and materials were used in comparison to [1]. Table 1 shows the differences between the two models, including the excitation sources used.
Both simulators used the same geometrical model with the same sources and material definitions. The goal was to reach the limits of the computational capabilities of the used tools up to a point where they would be unable to simulate the whole structure and obtain valid EM field values for post-processing analysis.
For the CST Microwave Studio simulations two computers were used: a local computer with 4 cores and 16 GB of RAM and a remote computer with 6 cores and 32 GB of RAM. For the CONCEPT-II simulations, a local computer with 4 cores and 16 GB was used initially but then for later simulations a server cluster was used which had 10 nodes available each one containing 6 CPUs and 32 GB of RAM.
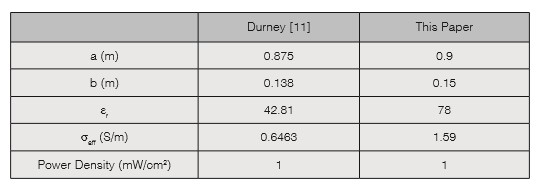
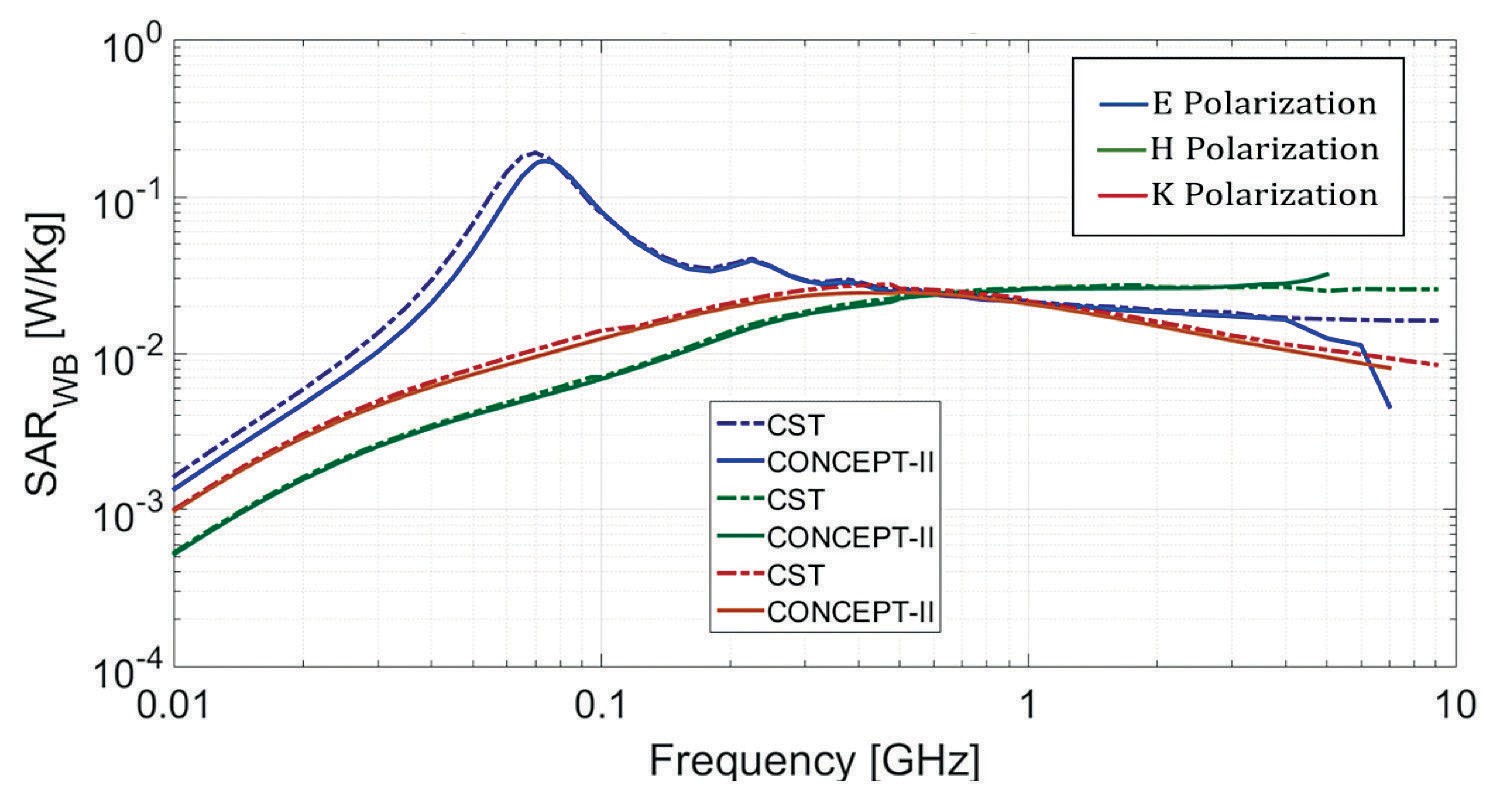
Figure 2 shows a similarity between the whole-body SAR of the previous research and this paper; differences may be due to slightly different body dimensions and material properties. There is also a good degree of correspondence between the results provided by both solvers. Considering that the two applied numerical methods are based on very different approaches to compute the fields, this indicates that the estimated values and observed trends are consistent.
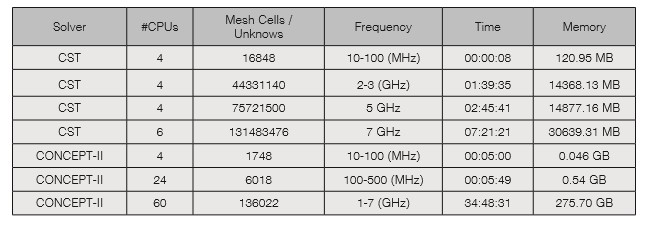
Computational capabilities differ for both tools but are close to each other. None of them reached the 10 GHz mark and results from CONCEPT-II (MoM) start to behave differently from 5 GHz for E and H polarization; this is attribute to limitations of the numerical method when calculating the field values. The use of electric and magnetic symmetry allowed the simulations to go further in frequency. Table 2 shows the computational resources used by both methods at various frequencies to calculate the whole-body SAR in E polarization.
Limitations were due to the available RAM for both tools. The higher the frequency, the bigger the amount of RAM needed to compute the fields. In table 3, the memory needed for both tools to run a simulation at 10 GHz is shown; each tool was run in a different computer and even though the MoM tool had more memory available, both reached an almost equal limit.

Whole-Body SAR on a prolate spheroid using physical optics
Due to the computational limitations of full wave simulations, alternative methods need to be used to calculate the absorption of energy by biological tissues. One of these methods is to use physical optics to calculate the absorbed power. The basic assumption is that all the energy transmitted into the body (prolate spheroid) is absorbed. This is a valid assumption as it has been found that for certain geometries the internally reflected rays may be neglected and from 6 GHz onwards, biological tissue has a depth penetration of 2.6 mm, which makes the assumption valid, that all transmitted energy is absorbed [21].
To implement this method the propagation vector of the incident wave is defined to lie in the XY plane, the formula is given by equation (2) and a is the angle of general incidence of the wave, which is defined in figure 1. The polarizations of the incident wave are represented by unit vector e1 and e2, where e1 is parallel to the plane defined by the major axis of the prolate spheroid and e2 is perpendicular to that plane.
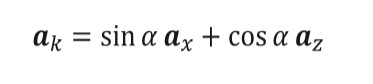 (2)
(2)
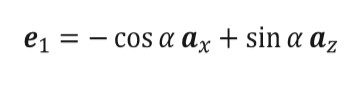 (3)
(3)
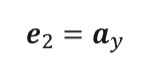 (4)
(4)The angle of incidence for every patch is obtained from equation (5) and once obtained the transmission angle can be found through equation (6).
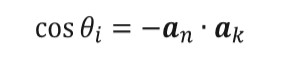 (5)
(5)
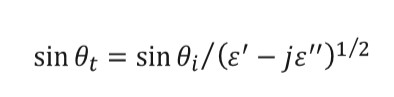 (6)
(6)Due to the prolate spheroid geometry, every patch has two reflection coefficients depending on the polarization of the incident wave. Equations (7) and (8) are used to calculate the values of the coefficients for each patch.
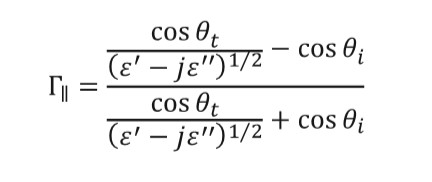 (7)
(7)
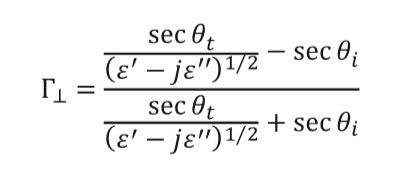 (8)
(8)Once the reflection coefficients are obtained, the transmission coefficients for each patch are calculated using equations (9) and (10).
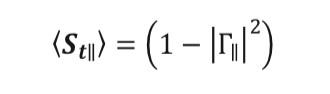 (9)
(9)
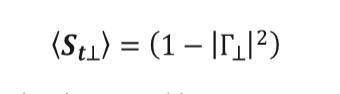 (10)
(10)These coefficients must be implemented in a proper manner, the incident electric field must be broken up into two components for each subarea: one parallel to the plane of incidence and one perpendicular to this plane. A method used to find these components of the incident electric field is to define a unit vector perpendicular to the plane of incidence on each patch and then find components of the incident wave polarization vector, which is parallel and perpendicular to this vector. A unit vector perpendicular to the plane of incidence is found in equation (11)[22].
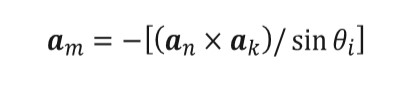 (11)
(11)Once this vector is obtained for each patch, equation (12) can be used to obtain the power absorbed from each patch for the parallel incident wave, where Si is the incident power density and AP are the projected area of each patch. For e2 is used, equation (13), with AP defined according to equation (14) for both cases.
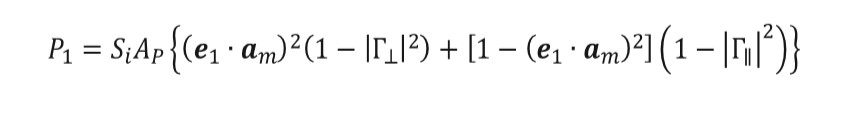 (12)
(12)
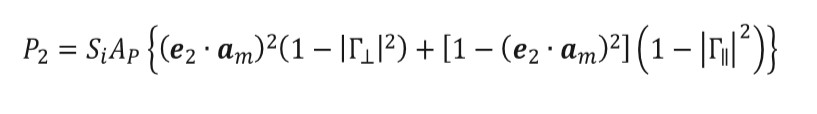 (13)
(13)
 (14)
(14)Based on this methodology, an in-house implementation was used to compute the whole-body SAR was obtained for 3 different wave polarizations on the prolate spheroid up to 100 GHz.
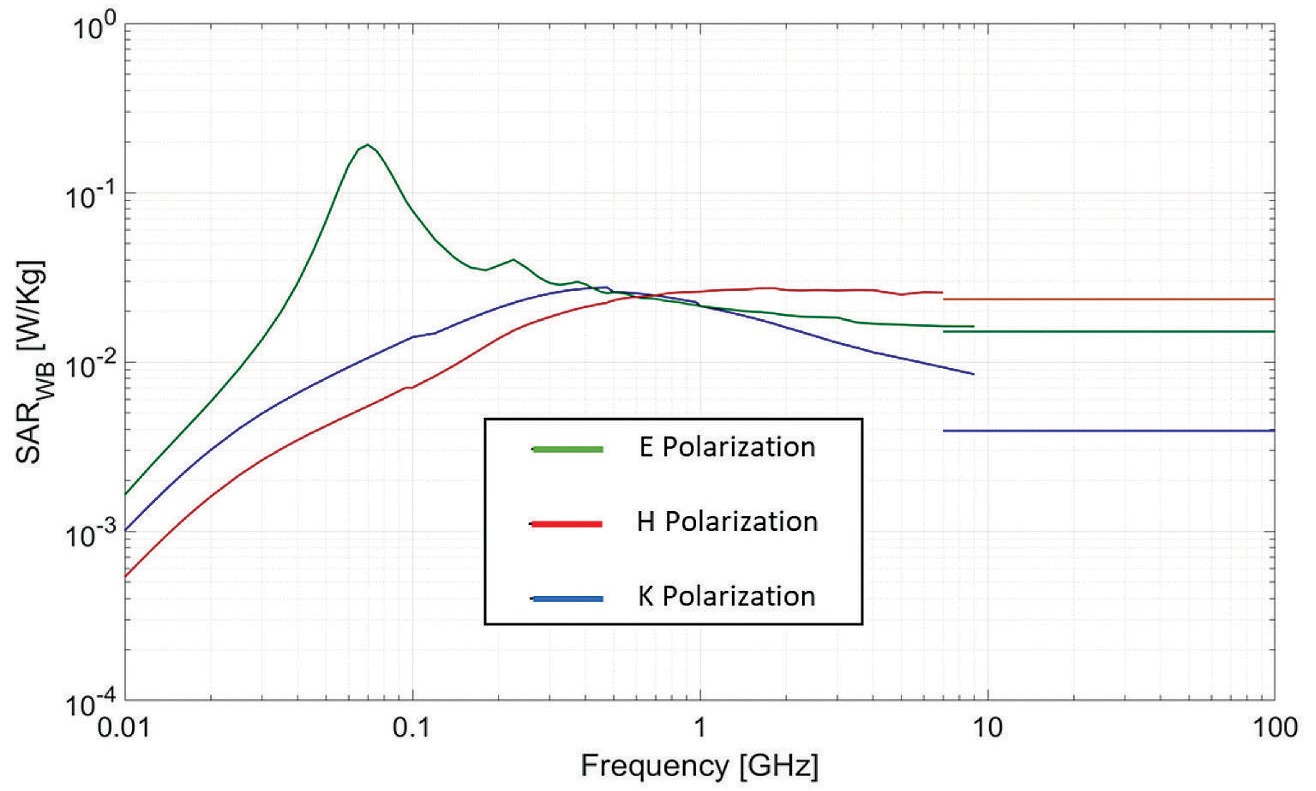
In Figure 3 the full frequency spectrum of interest is visualized. The whole-body SAR obtained for the high-end range (10 GHz - 100 GHz) behaves similarly to [11] for at least two of the three polarizations, which means that a good degree of correspondence was obtained with the method applied even with the small variations made between models.
For K polarization there is an obvious difference between the values from the full wave simulation and the optical approach that is not present on the other two. One possible reason for this variation is the limitations of the method used, which needs a nearly perfect “wall” of incidence or the least amount of curvature where the fields are radiating. This limitation is heavily compromised on K polarization due to the fields radiating to the curved part of the spheroid. There is also an important difference in the distance that EM fields must travel between the three polarizations. While E and H polarization traverses the narrowest part of the spheroid, K polarization must travel across the widest part of it.
Conclusions
Even though contemporary general-purpose tools for EM computation are better optimized and there is more access to powerful computational resources, high-frequency simulations for electrically large lossy dielectric bodies are still challenging. Due to the wavelength size in comparison to the size of the model of interest and the related discretization requirements, material properties, and other factors, it is difficult to study the higher parts of the frequency spectrum with traditional full-wave numerical methods.
In this work, an alternative to overcome part of these computational limitations was discussed and it was shown how physical optics could be used to obtain the power absorbed by an electrically large body in the multi GHz range. However, in its current form, the approach has limitations and works well in some scenarios only. Future work will have to address these limitations as well as a more detailed validation of the method against other alternatives.
References
[1] A. Hirata, O. Fujiwara, T. Nagaoka y S. Watanabe, “Estimation of Whole-Body Average SAR in Human Models Due to Plane-Wave Exposure at Resonance Frequency,” IEEE Transactions on Electromagnetic Compatibility, vol. 52, nº 1, pp. 41-48, 2010.
[2] E. Conil, A. Hadjem, A. Gati, M.-F. Wong y J. Wiart, “Influence of Plane-Wave Incidence Angle on Whole Body and Local Exposure at 2100 MHz,” IEEE Transactions on Electromagnetic Compatibility, vol. 53, nº 1, pp. 48-52, 2011.
[3] C. Lazarescu, I. Nica and V. David, “SAR in human head due to mobile phone exposure,” 2011 E-Health and Bioengineering Conference (EHB), Iasi, 2011, pp. 1-4.
[4] Mai Lu and Xiao-Yan Wu, “Study of specific absorption rate (SAR) induced in human endocrine glands for using mobile phones,” 2016 Asia-Pacific International Symposium on Electromagnetic Compatibility (APEMC), Shenzhen, 2016, pp. 1084-1086.
[5] P. Dimbylow y W. Bolch, “Whole-body-averaged SAR from 50 MHz to 4 GHz in the University of Florida child voxel phantoms,” Physics in Medicine and Biology, vol. 52, pp. 6639-6649, 2007.
[6] M. M. Búrdalo, A. Martín, M. Anguiano y R. Villar, “Comparison of FDTD-calculated specific absorption rate in adults and children when using a mobile phone at 900 and 1800 MHz,” Physics in Medicine and Biology, vol. 49, pp. 345-354, 2004.
[7] T. Nagaoka, E. Kunieda y S. Watanabe, “Proportion-corrected scaled voxel models for Japanese children and their application to the numerical dosimetry of specific absorption rate for frequencies from 30 MHz to 3 GHz,” Physics in Medicine and Biology, vol. 53, pp. 6695-6711, 2008.
[8] P. J. Dimbylow y O. P. Gandhi, “Finite-difference time-domain calculations of SAR in a realistic heterogeneous model of the head for plane-wave exposure from 600 MHz to 3 GHz,” Physics in Medicine and Biology, vol. 36, nº 8, pp. 1075-1089, 1991.
[9] M. Popović, Q. Han, and H. Kanj, “A Parallel Study of SAR Levels in Head Tissues for Three Antennas Used in Cellular Telephones: Monopole, Helix and Patch,” The Environmentalist, vol. 25, no. 2-4, pp. 233–240, 2005.
[10] N. Chahat, M. Zhadobov, L. Le Coq, S. I. Alekseev y R. Sauleau, “Characterization of the Interactions Between a 60-GHz Antenna and the Human Body in an Off-Body Scenario,” IEEE Transactions on Antennas and Propagation, vol. 60, nº 12, pp. 5958-5965, 2012.
[11] C. H. Durney, Radiofrequency Radiation Dosimetry Handbook. Springfield, VA: National Technical Information Service, 1978.
[12] E. Cocherova, J. Surda, O. Ondracek and V. Stofanik, “RF Field Orientation Influence on the Specific Absorption Rate in a Biological Object,” 2008 14th Conference on Microwave Techniques, Prague, 2008, pp. 1-3.
[13] Z. Pšenáková y M. Beňová, “Evaluation of SAR (Specific Absorption Rate) in multilayer structure of biological tissues near ear with cochlear implant,” 2017 18th International Conference on Computational Problems of Electrical Engineering (CPEE), Kutna Hora, 2017, pp. 1-3.
[14] E. Cocherova, J. Surda, J. Pucik, and V. Stofanik, “Dependence of the RF field absorption on the human body dimensions,” 2009 19th International Conference Radioelektronika, 2009.
[15] J. A. Carballo-Madrigal, H.-D. Brüns, R. Rímolo-Donadio y C. Schuster, “Full-Wave Simulation of Body Absorption due to Radiated Fields at GHz Frequencies,” Tecnología en Marcha, 2018.
[16] A. G. Canseven and N. Seyhan, “Ellipsoid models for human and guinea pigs exposed to magnetic fields,” 2003 IEEE International Symposium on Electromagnetic Compatibility, 2003. EMC ‘03., Istanbul, 2003, pp. 1227-1231 Vol.2.
References
[17] C. Furse, D. Christensen, and C. Durney. “Basic introduction to bioelectromagnetics,” 1st Ed. Boca Raton, Florida, USA: CRC Press, 2009.
[18] D. M. Pozar, Microwave engineering. New York, NY: Wiley, 1998.
[19] Computer Simulation Technology (CST). Microwave Studio (MWS). [Available Online]: http://www.cst.com.
[20] Electromagnetic Theory Institute, Technische Universität Hamburg (TET-TUHH). CONCEPT-II. [Available Online]: http://www.tet.tu-harburg.de/concept/
[21] H. J. Liebe, G. A. Hufford, and T. Manabe, “A model for the complex permittivity of ice at frequencies below 1 THz,” International Journal of Infrared and Millimeter Waves, vol. 12, no. 7, pp. 677–682, 1991.
[22] G. I. Rowlandson and P. W. Barber, “Absorption of higher-frequency RF energy by biological models: Calculations based on geometrical optics,” in Radio Science, vol. 14, no. 6S, pp. 43-50, Nov.-Dec. 1979.

