



La incertidumbre y la subjetividad en la toma de decisiones: una revisión desde la lógica difusa
Uncertainty and subjectivity in decision making: a revision from fuzzy logic
La incertidumbre y la subjetividad en la toma de decisiones: una revisión desde la lógica difusa
LÚMINA, núm. 14, 2013
Universidad de Manizales
Resumen: El objetivo de este artículo, es presentar, de manera introductoria, aspectos existentes que permiten relacionar la lógica difusa con la toma de decisiones. Se inicia con una breve explicación de los elementos básicos, en un proceso de toma de decisiones, enfatizando en el ambiente de incertidumbre y en los aspectos subjetivos presentes en el mismo. Posteriormente, se realiza un acercamiento a la lógica difusa a través de algunos ejemplos, herramientas, conceptos generales y relaciones existentes con la incertidumbre y con la subjetividad, en general. Finalmente, se presenta un ejemplo y un listado de obras y trabajos realizados en torno a la toma de decisiones desde esta nueva lógica.
Palabras clave: Lógica Difusa, toma de decisiones, ambientes de certeza, ambientes de riesgo, ambiente de incertidumbre, función de pertenencia, subjetividad.
Abstract: This paper aims at giving and introduction to some aspects which allow relating fuzzy logic with decision making. It starts with a brief explanation of the basic elements in a process of decision making and emphasizes in uncertainty environments and in the subjective aspects that appear in such processes. After that, I intend to give an introduction to fuzzy logic through some examples, tools, general concepts and existing relations with uncertainty and subjectivity in general. Finally, I give an example and a list of works about decision making from this new logic.
Keywords: Fuzzy Logic, Decision Making, Certainty Environment, Risk Environment, Uncertainty Environment, Subjectivity.
Introducción
“… es así que la realidad, aunque precisa en sí misma, sólo ha podido ser captada a través de algunos de sus aspectos, lo que ha llevado a simplificarla y le ha quitado precisión”. Kauffman y Gil Aluja.
La toma de decisiones es un proceso inherente y determinante en el ambiente económico; como fenómeno social, la economía, tanto en sus ámbitos macro y micro, se desarrolla y evoluciona a partir de las decisiones tomadas por sus participantes, explicitando la labor y responsabilidad directa de los sujetos que en ella intervienen.
Tomar decisiones, lleva consigo, establecer y determinar una amplia gama de factores, alternativas y variables propias del espacio donde se plantean y se desarrollan los problemas de decisión; por ello, es necesario comprender, interpretar y modelar la realidad y el contexto donde se enmarcan dichos problemas. Sin embargo, lograr modelar los fenómenos diarios en cualquier ámbito, es una labor bastante complicada, dado que, producir un reflejo fiel del mundo cambiante, interpretar los distintos matices del medio, y establecer un micro mundo que se asemeje a la situación real estudiada, es una tarea muchas veces complicada, debido, en gran parte, al dinamismo del universo y a la incertidumbre frente a la futura mutación.
Las matemáticas, a través de la historia, han permitido modelar la realidad y sus fenómenos, realizando abstracciones y representaciones del entorno, sin embargo, los alcances han estado mediados por la formalización de una “realidad acomodada”, es decir, que, generalmente, se realiza un proceso adaptativo del ambiente a los modelos matemáticos. En este proceso adaptativo, son necesarios los datos precisos y bien definidos, es imperante establecer una serie de condicionamientos sobre la ocurrencia específica de los escenarios iniciales; difícilmente, se consideran las inestabilidades de los procesos y las rupturas del comportamiento, siendo así, el establecimiento de leyes de probabilidad, una las herramientas más frecuentes, cuando el comportamiento del fenómeno se hace incierto, hecho bastante palpable en los fenómenos de índole económico.
Particularmente, las herramientas matemáticas que han permitido dar luces a una teoría de las decisiones1, han estado enmarcadas por el trabajo sobre datos de tipo cuantitativo, bien sea, en sus variables como en sus posibles escenarios futuros, estos últimos, determinados, al menos, por alguna probabilidad. En la literatura, se encuentran varios métodos que permiten abordar la toma de decisiones en estos casos; las matrices de resultados, los árboles de decisión, la programación lineal, la teoría de colas, la teoría de redes, la programación entera, la simulación, el análisis de Markov, entre otros.
Este tipo de técnicas, no son una fuente de respuestas automáticas para “todos” los tipos de problemas alrededor de la toma de decisiones, pues, se limita al estudio de variables tangibles, en el sentido estricto de su medición y, deja de lado, aspectos cualitativos propios del lenguaje y de la condición humana.
Es por ello, que, a la par, también han surgido métodos con gran participación de las matemáticas, que han permitido trabajar las variables de tipo cualitativo, la información imprecisa, las valoraciones, las opiniones de expertos y los ambientes en donde el dinamismo, la subjetividad y la incertidumbre se hallan presentes en gran medida; algunos de ellos son: el criterio maximax, maximin, criterio de Hurwicz, criterio de razón insuficiente de Laplace, la lluvia de ideas, la sinéctica, decisiones por consenso, la técnica Delphi, entre otras. Estas técnicas han permitido el tratamiento y el control de fenómenos más propios de la cotidianidad, empero, presentan su mayor dificultad en la fiabilidad de los resultados debido, en parte, a la gran “carga emocional” en los juicios de valor que se obtienen de los expertos, o, incluso, de la postura del agente decisor; dichos juicios se basan en las creencias, opiniones y expectativas de los mismos.
El carácter subjetivo de estas últimas técnicas, generan inseguridad frente a la eficiencia de su aplicación; si bien es cierto, que permiten un trabajo más consciente y racional para la elección de una decisión; el éxito depende del criterio y experticia de quien aplique la técnica. Es por ello, que es fundamental, el establecimiento de una teoría que permita controlar, medir y modelar los escenarios donde prime la información imprecisa, contrarrestando la carga subjetiva.
Frente a este planteamiento, surge una alternativa de tipo teórico-matemático que permite describir la dimensión ambigua con mayor precisión, una herramienta matemática que facilita captar la incertidumbre y la subjetividad, dando paso al estudio de las posibilidades2 más allá que el de las probabilidades; una teoría, que de manera paralela, brinda luces al proceso de la toma de decisiones en el marco de variables y escenarios de información imperfecta y donde se encuentran inmersos elementos de tipo cualitativo. Dicha teoría, ha sido denominada por su creador, como “lógica difusa”3.
Este trabajo, busca realizar un primer acercamiento a la lógica difusa a propósito de la teoría de las decisiones. Para ello, se realiza una revisión bibliográfica de los aspectos generales y constitutivos, tanto de la toma de decisiones como de la lógica difusa; plasmando así, los elementos básicos de cada una de las teorías en el marco del tratamiento de la subjetividad y de la incertidumbre. Finalmente, por medio de un ejemplo, se busca mostrar uno de los aportes que la teoría de la lógica difusa brinda a la toma de decisiones, objetando, en gran medida, lo establecido por Córdoba (2004)4; de igual forma, se presenta un listado de trabajos desarrollados acerca de esta relación y que sirven como punto de referencia para futuros trabajos.
Ambientes de incertidumbre en la toma de decisiones
El estudio frente a la toma de decisiones, lleva consigo, un análisis inherente de la situación particular a la que se enfrenta el agente decisor; las variables que intervienen, los datos conocidos y su precisión, son algunos de los elementos que se deben tener en la cuenta, a la hora de llevar a cabo este estudio. Sin lugar a dudas, las matemáticas, a través de la historia, han permitido modelar y dar luces al tratamiento de la toma de decisiones; el surgimiento de diversas teorías, en su mayoría de tipo probabilístico, han permitido, cada vez, ser más acertados y objetivos en cuanto a la elección que se tome en un determinado contexto. Pero, bien lo plantea Córdoba (2004), existen elementos propios del ser humano que, en su totalidad, las matemáticas no pueden determinar, aunque exista una luz para su tratamiento:
Cabe pensar, si es posible sistematizar matemáticamente algo tan etéreo como la decisión humana. Es evidente, que lo que no se puede pretender, es convertir al hombre en un autómata, y que un ordenador programado adecuadamente, sea capaz de generar las decisiones que tomaría un cerebro humano porque, en este caso, se supondría que todos los hombres serían iguales. Pero, lo que sí se puede hacer, es utilizar las matemáticas y la estadística para aconsejar al sujeto humano cuál podría ser la mejor decisión o conjunto de decisiones a tomar dentro de un conjunto de alternativas. (Córdoba, 2004, p. 29)
Por lo anterior, aunque han sido innumerables los aportes matemáticos frente a este aspecto, es básico el conocimiento y la precisión de una gran cantidad de datos; en particular, es imperante el establecimiento concreto de las variables a trabajar, su adecuada definición y parámetros de medición. Matemáticamente, al plantearse un modelo que describa un fenómeno o que trate de describir su comportamiento, se parte de una serie de condiciones o premisas que deben cumplir las variables para que el modelo sea apto. En su mayoría, las variables que intervienen en un hecho real, deben ser adaptadas a un modelo particular y abstracto que ha sido diseñado para que la realidad encaje, de cierta forma, y pueda modelarse de la manera más acorde a la situación específica.
Durante muchos siglos se ha sostenido que “la naturaleza está obligada a seguir ciertas reglas que conducen a estructuras basadas en la certeza. Esto, queda ya patente en las leyes de Newton y, curiosamente, las que se han considerado grandes revoluciones del siglo XX, la mecánica cuántica y la relatividad, no han hecho más que confirmar esta visión” (Gil Aluja, 1997, p. 291)
Es así, como, hasta cierto punto, las matemáticas se han quedado cortas al tratar de crear un reflejo fiel de la realidad, pues las variables se deben adaptar a los fenómenos y no los fenómenos a las variables; en un contexto particular de estudio, se debe considerar toda una amplia gama de posibilidades, perturbaciones, cambios, complejidades, no linealidades, caos y evolución en el análisis del fenómeno particular. En palabras de Gil Aluja (2009).
Las estructuras lineales, tan aceptadas tradicionalmente, resultan cada vez más pobres para interpretar la globalidad de los fenómenos. Su empleo se va reduciendo a medida que avanzan las técnicas de colección y tratamiento de la información. Cada vez, resulta más difícil hacer caber en los esquemas clásicos las complejas realidades actuales. (Gil Aluja, 2009. p. 2)
Este panorama general de las matemáticas y su abstracción de la realidad, permite pensar en la necesidad de establecer una teoría, que permita mejorar las técnicas existentes frente a la toma de decisiones en contextos específicos, dominados por la incertidumbre y la subjetividad. Sin embargo, para ello, es preciso describir y establecer el punto de partida teórico en cuanto a la estructura básica frente a la toma de decisiones.
Abordar un estudio sobre la metodología para la toma de decisiones, implica realizar una descripción de los elementos constitutivos de un proceso de decisión, que de acuerdo con lo establecido por Córdoba (2004) son los siguientes:
• La existencia de un conjunto de opciones o alternativas,
• El ambiente o contexto estructural en el que el problema se suscita, y que se concreta en un conjunto de estados de la naturaleza
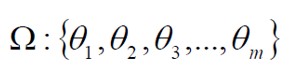
• Una función de evaluación de los resultados, que establezca las consecuencias asignables de la aplicación de cada opción o alternativa en los diversos posibles estados de la naturaleza,
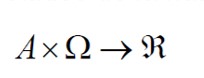
• Esta función es una aplicación del producto cartesiano del conjunto de alternativas y el conjunto de estados de la naturaleza, en el conjunto de los números reales; con lo que sus elementos serán:
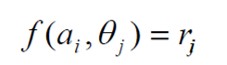
A esta función de evaluación, se denomina función de utilidad de los resultados.
Con estos elementos definidos, se establece entonces la matriz de decisión dada en la figura 1.
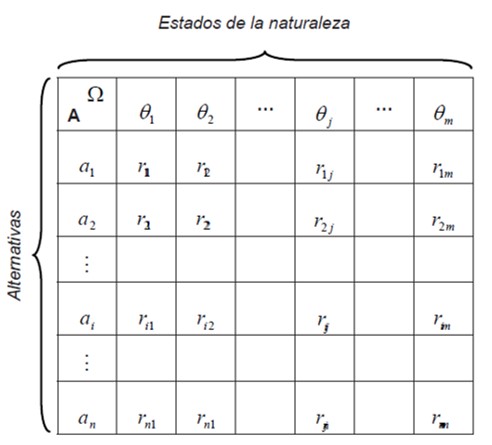
Dicha matriz, presenta una forma esquemática de organizar las posibles alternativas de acuerdo con su estado de la naturaleza particular. Un ejemplo presentado por Córdoba (2004) y que permite clarificar los elementos mencionados y la estructura de la matriz, es el siguiente:
Un sujeto económico se plantea el problema de cómo invertir un determinado volumen de capital en valores bursátiles y que, después de un análisis cualitativo inicial, encuentra que las mejores acciones en las que invertir son: a1, a2 y a3. Al estudiar la posible evolución de la situación económica durante el período de tiempo en el que planea mantener invertido su capital, el sujeto contempla tres posibilidades:
• Existencia de inflación.
• Estabilidad en precios.
• Depresión económica.
A la vista de ello, su estimación de cuáles serían los resultados económicos que podrían derivarse de la decisión adoptada, bajo la hipótesis de que invertiría todo su capital, exclusivamente, en uno de los tres valores preseleccionados, sería el presentado en la figura 2.
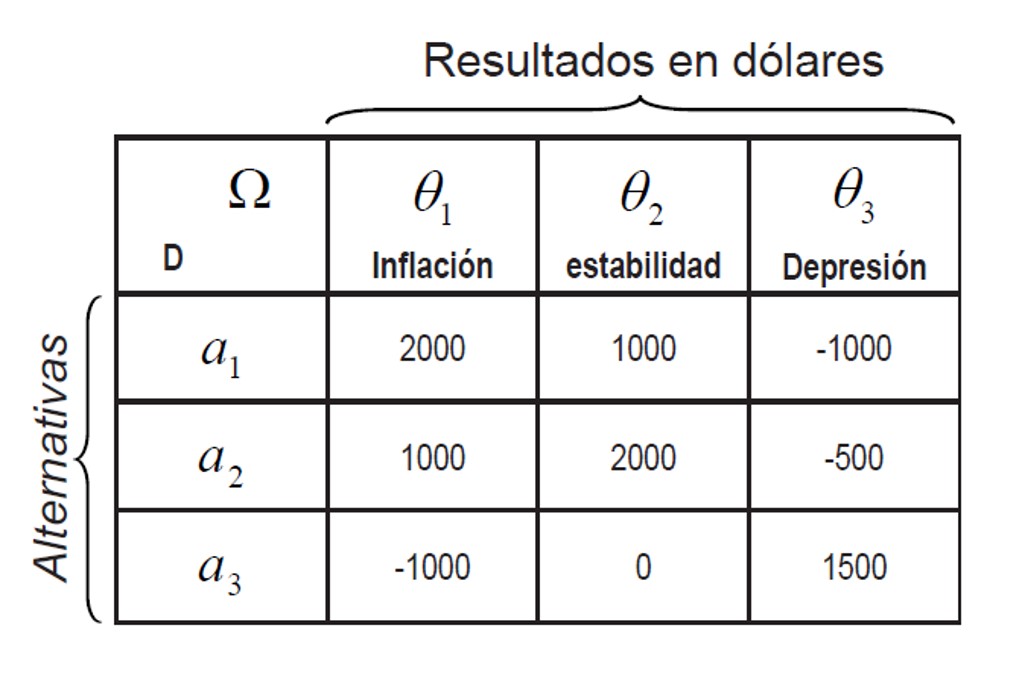
Ahora bien, la variedad de resultados, tanto de alternativas como de resultados, se debe a la incorporación de la existencia de incertidumbre; no saber a ciencia cierta lo que ocurrirá en el futuro con la situación económica es el factor con mayor complejidad al que se enfrenta el decisor a la hora de realizar la mejor elección.
Sin embargo, esta incertidumbre, dependiendo de las herramientas y de la concreción de los datos trabajados, determina diversos contextos, es decir, los estados de la naturaleza varían o se concretan según el grado, manejo o mitigación que se pueda dar a dicha incertidumbre, estableciendo así, lo que se denomina dentro de la teoría, diversos ambientes. En particular, se definen los siguientes (Córdoba, 2004):
• Ambientes de certidumbre o certeza: cuando son conocidas con certeza todas las alternativas, y los resultados que de ella se derivan, no existiendo ninguna incertidumbre que afecte el problema, se generan resultados bien definidos e invariables. Al tomar la decisión sólo se debe pensar en la alternativa que genera mayor beneficio.
• Ambientes de riesgo: se conocen las posibles alternativas pero los resultados que de ellas se derivan, pueden manifestarse de diferente manera, en función de una determinada ley de probabilidad, que suponemos conocida y que rige la posibilidad de acaecimiento de los diferentes estados de la naturaleza. Se trata, por lo tanto, de un problema de naturaleza estocástica y, en consecuencia, susceptible de ser probabilizable.
• Ambientes de incertidumbre: se conocen las posibles alternativas, los resultados que de ella se derivan pueden manifestarse de diferente manera, pero, o bien, no se trata de un fenómeno probabilizable, o bien, se desconoce la ley de probabilidad por la que se rige el acaecimiento de los diferentes estados de la naturaleza.
Los estados de incertidumbre son, en general, reflejos más precisos de la realidad, se presentan con mayor frecuencia de lo esperado, en esencia la vida misma, con su permanente aceleración, hace que los fenómenos cambien con inusitada rapidez, de tal manera, que cuando se ha conseguido un modelo apto para una determinada situación, hay que modificarlo porque ésta, ya ha variado. El decisor, se enfrenta así, ante un mundo regido tanto por la mutabilidad como por la incertidumbre.
En la misma línea, es claro señalar, que no es posible admitir que los conocimientos sólo pueden ser considerados como científicos, si son susceptibles de medición ya que, en este caso, las ciencias sociales carecerían de tal carácter. No obstante, esta ha sido una posición mantenida en muchas circunstancias con total intransigencia. La noción de azar se halla asociada a una idea de medida a través de la probabilidad. La incertidumbre es recogida de manera subjetiva asociándose a hechos no probabilizables, como el concepto de sensación y la noción de estimación. Tanto una cosa como la otra, son fundamentalmente subjetivas (Kaufmann, A. Gil Aluja, J. 1993)
Se presenta así, un panorama más amplio; ambientes en donde la ocurrencia de un fenómeno no se puede simbolizar por el concepto de aleatoriedad, donde se da cabida a problemas con una serie de criterios subjetivos que se convierten en información relevante, e incluso, fenómenos tan complejos, que según lo plantearía Córdoba (2004) “no se puede recurrir a procedimientos matemáticos o estadísticos para tomar una decisión racional”.
Afirmación que será refutada con la presentación de la lógica difusa.
El siguiente ejemplo ayudará a la comprensión de los ambientes descritos anteriormente y clarificará la noción de incertidumbre planteada:
El jefe de producción de una fábrica de vehículos tiene que plantear cuál es la mejor ruta de la cadena de producción para las instalaciones de la empresa. Después de estudiar diferentes rutas, llega a la conclusión, de que hay dos que son las mejores, una de ellas, que pasa por el centro de la fábrica, con diferentes giros en función de las máquinas instaladas y otra, que bordea la fábrica de derecha a izquierda, más larga, pero sin tener que hacer giros, al no haber ninguna máquina instalada en la ruta.
En la ruta que pasa por el centro de la fábrica, se da el caso de que cuando una demanda, baja de producción, el recorrido de los vehículos por la cadena de producción sería rápido, y tardaría aproximadamente 30 minutos, mientras que si hay una demanda alta, los tiempos de espera en la cadena hacen que se tarde 60 minutos desde que se inicia el trabajo en un automóvil hasta que se acaba.
En la ruta que bordea la fábrica, se consigue una uniformidad en los tiempos de la cadena de producción, que pasa a ser de 48 minutos por automóvil, independiente de la demanda.
Lo que el jefe de producción desea saber es, cuál de las dos rutas debe implantar en la fábrica. (Córdoba, 2004. p 38)
Para este problema, el conjunto de alternativas está claramente definido:
a1: ruta por el centro de la fábrica.
a2: ruta bordeando la fábrica.
El conjunto de estados de la naturaleza está, así mismo, definido:
q1: Demanda baja de producción
q 2 : Demanda alta de producción.
Si el sujeto decisor supiese cómo iba a estar la demanda de automóviles, el problema de decisión se plantearía en ambiente de certidumbre.
Sin embargo, si el jefe de producción no sabe cómo va a ser la demanda, se estaría ante un problema de decisión en el que existe aleatoriedad y, que puede manifestarse, en ambiente de riesgo o en ambiente de incertidumbre, según se pueda considerar el fenómeno como probabilizable o no.
Si el jefe de producción, según su experiencia, considera que la demanda puede estar baja con una determinada probabilidad “p”, y lógicamente, puede estar alta con una probabilidad “1-p”, se estaría ante un problema en ambiente de riesgo.
Si el jefe de producción, no es capaz de hacer una estimación de cómo evolucionará la demanda en los próximos meses, entonces, se estaría ante un problema de decisión en ambiente de incertidumbre.
La forma de abordar dichos ambientes es lo que concierne, de ahora en adelante. Sin embargo, el interés particular de este escrito está en cómo y bajo qué herramientas se pueden abordar los ambientes de incertidumbre; frente a la certeza y el riesgo, los tratados son numerosos y los modelos han sido ampliamente desarrollados y difundidos, pues la teoría matemática existente y las variables propias de estos ambientes, se funden en modelos que asemejan la realidad subyacente.
El nacimiento, no hace más de 50 años, de una nueva lógica, denominada lógica difusa, “fuzzy logic” o lógica borrosa y desarrollada por Lotfi A. Zadeh hacia 1965 dará luces al tratamiento de los ambientes de incertidumbre pero, en general, a todos aquellos contextos donde las variables no estén establecidas en términos exactos o por lo menos probabilizables.
A continuación, el propósito es presentar un primer acercamiento a la esencia sobre la cual versa dicha lógica.
Una primera idea de la lógica difusa
Las matemáticas, durante muchos años, han sido fundamentadas bajo la lógica binaria aristotélica, que plantea como principio, el ser o no ser, el pertenecer o no pertenecer, lo cierto o lo falso, formalizado, este hecho, un poco en 1854 con George Boole, quien planteó la forma de manipular y simplificar problemas lógicos y filosóficos cuyos argumentos admiten dos estados (verdadero o falso) por procedimientos matemáticos.
Más adelante, hacia principios del siglo XX, Lucasiewicz amplía este concepto, introduciendo la lógica multivalente en la que plantea, la existencia de tres valores de verdad; verdadero, falso e indefinido, uno de los primeros acercamientos para comprender mejor el mundo que nos rodea. La realidad, no siempre permite el acto simplificativo de la lógica bivalente, no todo es blanco o negro, sino que existen situaciones intermedias, toda una gama de grises que, hasta hace poco, quedaban fuera de un posible tratamiento científico. Más aún, cuando se refiere al cerebro humano, las situaciones existentes son difíciles de razonar, si solamente se tiene el todo y la nada.
En la cotidianidad se encuentran fenómenos que plantean dificultades para su definición y que sólo pueden ser estimados de manera subjetiva. Teniendo en cuenta que la pretensión de la ciencia es, ante todo, la investigación de nociones objetivas se tropieza con tal dificultad, desde esta perspectiva, de representar la realidad en toda su dimensión. Este problema es mucho más agudo en las ciencias humanas cuyo contenido abarca una zona mayor de subjetividad que de aspectos objetivos (Kaufmann, Gil Aluja. 1993).
Es así, como en la década de los años sesenta, Lotfi A. Zadeh plantea “fuzzy logic”, una lógica que pretende abordar mejor la realidad circundante, pues, como lo plantean Kaufmann y Gil Aluja (1993).
La teoría de los subconjuntos borrosos, lógica difusa o borrosa, es una parte de las matemáticas que se halla perfectamente adaptada al tratamiento tanto de lo subjetivo como de lo incierto. Es un intento de recoger un fenómeno tal cual se presenta en la vida real y realizar su tratamiento sin intentar deformarlo para hacerlo preciso y cierto. (Kaufmann, A. Gil Aluja, J. 1993, p. 18)
El nuevo tratamiento de la incertidumbre, a partir de los conceptos borrosos5, ha dado lugar a una manera distinta de pensar que reune el rigor del razonamiento secuencial con la riqueza de la imaginación inherente a la borrosidad.
Son muchos los contextos donde se evidencian conceptos difusos, por ejemplo, en el ámbito económico, el concepto de PIB (producto interno bruto) genera ambigüedad debido a que, en sí mismo, el concepto “valor del dinero”, es indeterminado, dependiendo así, de variables como son la inflación, los tipos impositivos, el tipo de interés o política externa e interna.
Más claramente, el concepto de “números de desempleados de un país” bajo una óptica detallada es algo bastante ambiguo, pues, como tal, dentro de él deberían estar aquellas personas con un trabajo informal o, incluso, aquellas personas que trabajan de medio tiempo, queriendo trabajar de tiempo completo; es decir, estas últimas distinciones, no pueden ser consideradas como personas empleadas o desempleadas, totalmente.
Estos tipos de variables van a poder ser abordados con la lógica difusa. Por lo tanto, es menester presentar una primera idea intuitiva de cómo funciona la teoría. No se pretende realizar una descripción detallada o axiomática de la lógica difusa, sólo se realiza un pequeño acercamiento a sus generalidades, como parte introductoria al lector.
En la lógica convencional, el concepto intuitivo de conjunto, determina una colección o agrupación de objetos, reunidos, usualmente, bajo una característica particular de dichos objetos. Decir que un conjunto está bien definido, implica poder establecer, de manera absoluta, si un elemento pertenece o no pertenece al conjunto sin ninguna ambigüedad. Ejemplo claro de ello, el conjunto de los números Reales, en donde podemos determinar, con toda certeza, si un número pertenece o no a él.
De esta manera, en la teoría de conjuntos clásicos se define una función de pertenencia;

Sin embargo, este proceso de clasificación por pertenencia, no es posible siempre en otro tipo de conceptos, por ejemplo, el grupo de personas altas, siendo el término “altas”, una expresión lingüística dotada de un carácter subjetivo o el grupo de personas jóvenes, cuando la connotación de juventud es una abstracción relativa.
Para este tipo de ambigüedades, la lógica difusa realiza una extensión de la función de pertenencia presentada con anterioridad. Para definir un conjunto difuso, es necesario establecer una función que permita asignar a cada elemento, un valor real que indica qué tanto pertenece al conjunto, por lo general, se considera dicho real en el intervalo [0,1]. Los valores más altos denotan mayor pertenencia, mientras lo valores más pequeños denotan poca pertenencia al conjunto. En el mismo orden de ideas, el 0 representa no pertenencia, mientras el 1 denota una pertenencia total. Por tanto, la función de pertenencia vendría representada así;
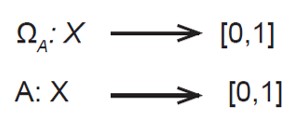
Donde la letra A denota, tanto al conjunto como a la función de pertenencia asociada. Por lo tanto, la segunda notación no generará ambigüedad y será la comúnmente usada.
El siguiente ejemplo muestra cómo es posible trabajar con este tipo de expresiones relativas y subjetivas que se referenciaban en los ejemplos de personas “altas” y “jóvenes”, a través del concepto de conjunto difuso. Ejemplo, presentado por Klir (1995).
La temperatura entre un rango [t1, t2] se caracteriza como una variable difusa y se da su representación en la figura 3, donde los estados de la variable difusa, aquí indicados, son conjuntos difusos que representan 5 conceptos lingüísticos: muy frío, frío, medio, caliente, muy caliente. Todos ellos definidos por la función de pertenencia;

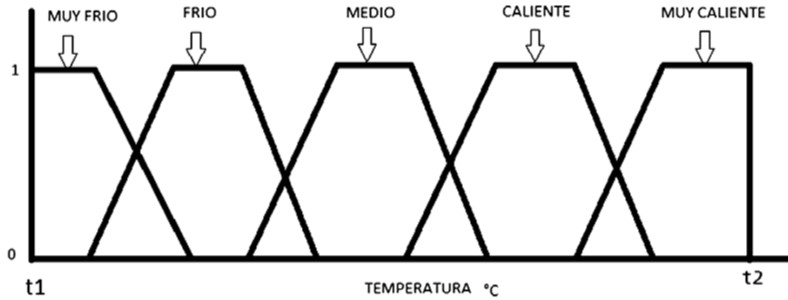
Una representación de la misma variable a través de los conjuntos clásicos se presenta en la figura 4.
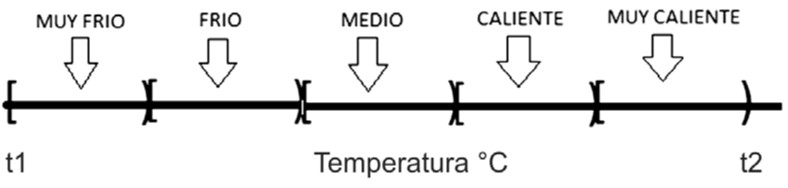
Evidentemente, la importancia de las variables difusas radica en la posibilidad de una transición gradual entre los estados definidos por los “valores” de la variable, lo que permite, el tratamiento de la incertidumbre generada por dicho lenguaje.
Se ha tratado de comparar en las figuras 3 y 4, el tratamiento de la variable con los conjuntos difusos y los conjuntos clásicos. En la primera parte, se observa la posibilidad de un elemento para pertenecer en diferente medida a dos conjuntos, sus niveles de pertenencia varían, sin la exclusión de alguno de ellos. Por el contrario, en el tratamiento con los conjuntos clásicos no se da esta alternativa, imposibilitando el análisis en los puntos fronterizos.
Un ejemplo más concreto y donde se define con mayor precisión la función de pertenencia o característica, es el relacionado con la “juventud”, en el que, una alternativa, sería considerar las categorías de personas jóvenes, de mediana edad y viejas, también, presentado por Klir (1995).
Para ello, se han definidos funciones de pertenencia trapezoidales A1, A2 y A3, estableciendo el siguiente diagrama, dado en la figura 5.
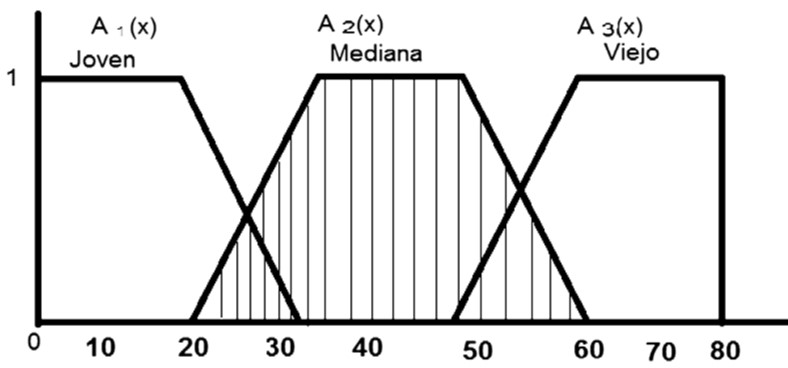
Estas funciones se pueden definir en el intervalo [0,80] como sigue:

Así, por ejemplo, una persona de 54 años en la lógica convencional debería estar clasificada, exclusivamente, como una persona de edad media o vieja; mientras que para la lógica difusa, esta persona, tiene un grado de pertenencia de 0,4 como persona de edad media y un grado de pertenencia de 0,6 como persona vieja.
Es importante aclarar que, en este sentido, el grado de pertenencia, representa la calidad expresada con un número entre 0 y 1, con la que un elemento pertenece a un determinado conjunto; es decir, la compatibilidad del elemento con el concepto representado por el conjunto.
No debe confundirse el concepto de probabilidad de pertenencia a un conjunto ordinario con el grado de pertenencia a un conjunto borroso. Aunque la función de pertenencia de un conjunto borroso puede tener cierto parecido con una función de probabilidad, cuando X es un conjunto numerable (o una función de densidad de probabilidad si X es continuo), hay diferencias sustanciales entre ambos conceptos. Así, no tiene porque cumplirse que la suma de los grados de pertenencia a distintos conjuntos borrosos sea la unidad, ni tampoco que el grado de pertenencia indique la ocurrencia de un determinado suceso en repetidas experiencias. Por ejemplo, si se indica que el grado de pertenencia del contenido de una botella al conjunto veneno mortal es 0,01, se está indicando, que el líquido no es prácticamente venenoso, aunque posea algunas trazas de veneno, por lo que podría no haber riesgo para su ingesta. Sin embargo, si se afirma que la probabilidad de que el líquido sea veneno mortal es de 0,01, el líquido podría ser completamente veneno mortal, aunque con una probabilidad baja y, por lo tanto, letal.
Es importante anotar, que un conjunto borroso queda caracterizado mediante su función de pertenencia. Esta puede expresarse de forma discreta, enumerando el grado de pertenencia para cada elemento del conjunto, o, mediante una definición matemática.
Por ejemplo, mediante definición matemática se observa en la figura 5 y su correspondiente formulación. Ahora bien, un conjunto borroso expresado mediante definición discreta puede ser el siguiente:

Partimos de un referencial, E= {a, b, c, d, e, f, g} y A representa el conjunto borroso. Dicho conjunto, hace referencia, por tomar un ejemplo similar al ya tratado, al concepto borroso de “edad de vigor para trabajar”, en donde E, representa un conjunto de siete personas y los números correspondientes a cada uno indica su grado de pertenencia a este concepto. Así, por ejemplo, la persona representada por g, con un grado de pertenencia de 0.9 sería establecida como la persona con mejor edad para trabajar.
En la mayoría de los casos, se emplean funciones de pertenencia definidas matemáticamente, ya que estas funciones permiten realizar estudios posteriores con mayor facilidad y son válidas para cualquier elemento dentro de su universo de discurso. Las funciones de pertenencia discretas, en principio, son sólo válidas para un conjunto de elementos, los empleados para definir la función; sin embargo, si se emplea algún algoritmo de identificación con los pares de datos 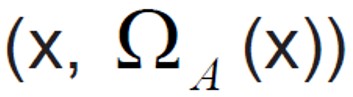 , o se define una función a trozos, se podrá obtener una expresión matemática que la represente.
, o se define una función a trozos, se podrá obtener una expresión matemática que la represente.
Otros ejemplos de funciones de pertenencia se muestran en la figura 6.
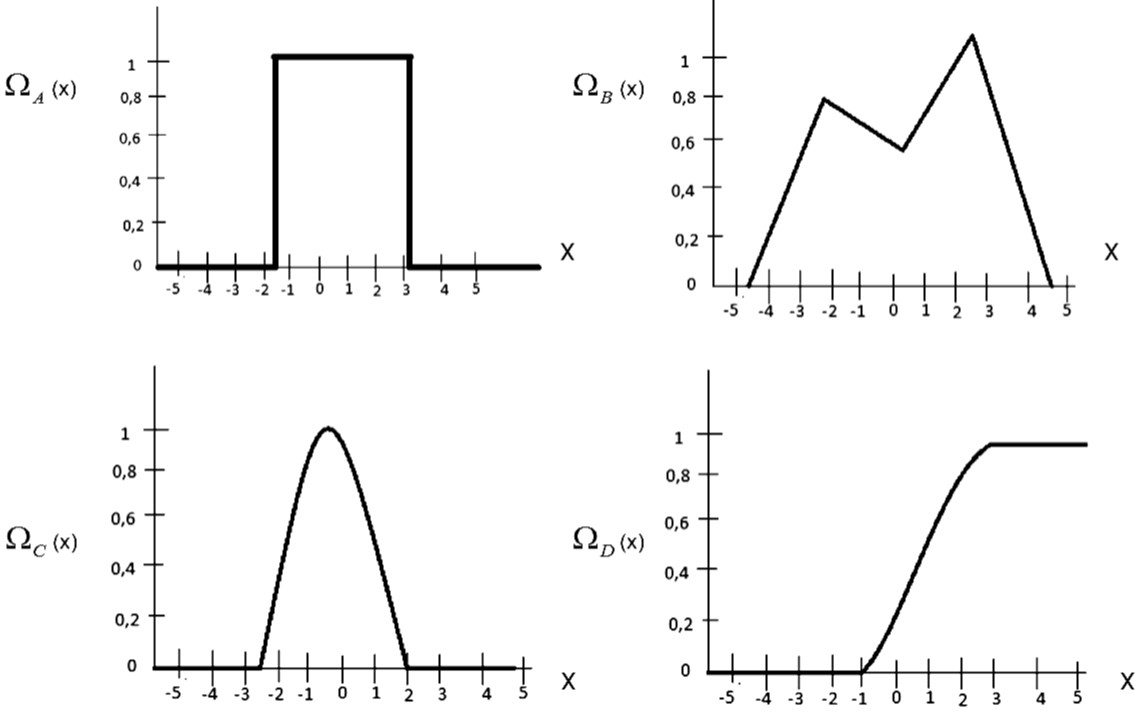
Todas estas funciones de pertenencia poseen universo de discurso X∈ [−5, 5], la primera,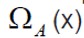 es la función de contenencia de un conjunto clásico, ya que sólo genera dos grados de pertenencia, mientras que las restantes son funciones de pertenencia borrosas;
es la función de contenencia de un conjunto clásico, ya que sólo genera dos grados de pertenencia, mientras que las restantes son funciones de pertenencia borrosas;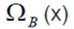 es una función de pertenencia no convexa definida a trozos,
es una función de pertenencia no convexa definida a trozos, 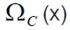 una gaussiana,
una gaussiana, 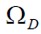 (x) una función de pertenencia S.
(x) una función de pertenencia S.
Este es sólo un pequeño abrebocas a la idea esencial de cómo funciona la lógica borrosa.
El propósito, a continuación, es mostrar algunos ámbitos donde se han venido haciendo desarrollos basados en la lógica difusa; por lo tanto, se presenta una síntesis de lo expuesto por Reig, Sansalvador, Trigueros (2000), donde se enlistan algunos campos diversos de las ciencias y sus aplicaciones. Posteriormente, se realiza un acercamiento a la recopilación de algunos trabajos acerca de la teoría de la toma de decisiones, realizada por el autor.
Algunas aplicaciones de la lógica difusa
En términos generales, puede establecerse que la lógica difusa lleva un desarrollo no inferior a medio siglo, por lo tanto, su crecimiento y aplicabilidad ha tenido gran difusión en diversas áreas del conocimiento, algunos de ellos, se presentan a continuación. Tabla 1.
| Gestión/sociedad | Inteligencia artificial/ información | Ingeniería de control | |
| Modelos humanos (1) | Planificación. Evaluación. Toma de decisiones. Organización. Relaciones humanas. | ||
| Imitación de la capacidad humana (2) | Sistemas de apoyo en la toma de decisiones. Sistemas de apoyo en el diagnóstico médico. | Sistemas expertos. Bases de datos | Procesos de control en operaciones mecánicas. Robótica. |
| Comunicación humana (3) | Equipamiento para personas con discapacidad. | Introducir la voz en cartas y figuras. Reconocimiento de imágenes. Búsqueda de voces. | |
| Otros (4) | Análisis de riesgo. Predicción de roturas. | Desarrollo de diversos razonamientos |
A continuación, se presenta un breve listado de trabajos y obras sobre el desarrollo de la teoría sobre la toma de decisiones con la lógica difusa o algunos estudios de casos aplicados desde esta perspectiva; Tabla 2.
| Autor(es) | Año | Obra |
| Bellamn R. Zadeh L | 1970 | Decision making in a fuzzy environment |
| Okuda, T., Tanaka, H., and Asai, K. | 1974 | Decision making and information in fuzzy events. |
| Jain, R. | 1976 | Decision-making in the presence of fuzzy variables. |
| Tanaka, H., Okuda, T., and Asai, K. | 1976 | A formulation of fuzzy decision problems and its application to an investment problem. |
| Bezdek, J., Spillman, B. and Spillman, R. | 1978 | A fuzzy relation space for group decision theory. |
| Jain, R. | 1978 | Decision-making in the Presence of Fuzziness and Uncertainty |
| Okuda, T., Tanaka, H., and Asai, K. | 1978 | A formulation of fuzzy decision problems with fuzzy information, using probability measures of fuzzy events. |
| Yanger R. | 1978 | Fuzzy decision making including unequal objectives. |
| Haage, C. | 1978 | Possibility and cost in decision analysis. |
| Zimmermann, J. | 1978 | Fuzzy Sets, decision-making and Expert Systems. |
| Nurmi, H | 1981 | Approaches to collective decision-making with fuzzy preference relations. |
| Yager, R. | 1981 | A new methodology for ordinal multiobjective decisions based on fuzzy sets. |
| Kacprzyk Janusz. | 1986 | A “down-to-earth” managerial decision making via a fuzzy-logic- based representation of commonsense knowledge. |
| Zimmermann, J. | 1990 | Decision-making in ill-structured environments and with multiple criteria(a). |
| Jablonowski, M | 1991 | Fuzzy logic and insurance decisions |
| Kaufmann A. Gil Aluja J. | 1993 | Nuevas técnicas para la gestión estratégica. Capítulo de libro. |
| Sakawa, M. | 1993 | Fuzzy Sets and Interactive Multiobjective Optimization |
| Adams, T. | 1994 | Retaining structure selection with unequal fuzzy project-level objectives. |
| Mario Fredizzi. | 1995 | Fuzzy approaches to modelling consensus in group decision support |
| Elizabeth Gurokac | 1996 | Fuzzy multiple criteria decision making for natural resource projects |
| Kleyle, R. de Korvin, A. Mc Laughlin, A. | 1996 | Decision making on the basis of expected cost variance: a fuzzy set approach. |
| C. Zopounidis, M. Doumpos | 1997 | A multicriteria method for sorting decision problems under uncertainty. |
| A. Morillas, B. Díaz, J. González | 1997 | A fuzzy multiple attribute decision proposal for evaluating environmental plans. |
| Luisa L. Lazzari, Emilio Machado, Rodolfo Pérez. | 1998 | El método Fuzzy-Delphi. Estimación del Cash – Flow a través de la opinión de expertos. |
| Luisa L. Lazzari, Emilio Machado, Rodolfo Pérez. | 1998 | El problema de selección de personal. |
| Luisa L. Lazzari, Emilio Machado, Rodolfo Pérez. | 1998 | Teoría de la decisión en condiciones de incertidumbre. |
| Bogdan Andronic | 2000 | Applications of fuzzy sets in issues of economic decisions and analysis. |
| Peñalva Rosales. L. | 2000 | Propuesta de la lógica difusa para la toma de decisiones. |
| Herrera, E. Herrera-Viedma, and L. Martínez. | 2000 | A fusion approach for managing multigranularity linguistic term sets in decision making. |
| Carrizo, M., Casparri, M. y Taboada, E. | 2000 | Una selección de canales de distribución a través de relaciones borrosas |
| Herrera, E. Herrera-Viedma, and F. Chiclana. | 2001 | Multiperson decision-making based on multiplicative preference relations. |
| Luisa L. Lazzari, Emilio Machado. | 2001 | Consideraciones acerca de los procesos de decisión híbridos. |
| Mallo, Paulino E.; Artola, María Antonia; Galante, Marcelo Javier; Martínez, Die- go; Pascual, Mariano Enrique y Morettini, Mariano. | 2003 | Aplicación del método Delphi a las decisiones financieras en situaciones de incertidumbre. |
| José Luis García-Lapresta, Bonifacio Llamazares. | 2003 | C Choosing a ranking of alternatives in a two-stage group decision procedure with individual linguistic assessments. |
| Gil Lafuente Anna Maria. | 2004 | La contabilidad y las técnicas de decisión. Capítulo de libro. |
| Maes, M. and Faber, M. | 2004 | Issues in utility modelling and rational decision making. |
| Vasant. P | 2005 | Fuzzy production planning and its application to decision making. |
| Gil Lafuente Jaime | 2006 | Nuevo instrumento de selección: el “índice de Descartes por superación-distancia”. |
| Gómez González, D | 2006 | Algunas aportaciones sobre representación de preferencias. |
| Florica Luban | 2006 | Modeling imprecision and subjectiveness for the multiattribute decisions |
| Mallo, Paulino E.; Artola, María Antonia; Galante, Marcelo Javier; Pascual, Mariano Enrique; Morettini, Mariano y Busetto, Adrián Raúl | 2006 | Aplicación de herramientas borrosas al balance scorecard. |
| José D. Bermúdez, José Vicente Segura, Enriqueta Vercher | 2007 | Modelos borrosos de optimización para la selección de carteras basados en intervalos de medias. |
| Mallo, Paulino E.; Artola, María Antonia y Morettini, Mariano. | 2009 | Decisiones financieras con programación lineal: diferentes estados de la naturaleza. |
| Cebi, S. Kahraman, C | 2010 | Fuzzy multicriteria Group decision making for real estate investments |
| Chin-Hung Liu | 2010 | A group decision-making method with fuzzy set theory and genetic algorithms in quality function deployment |
| G.W. Weia, J.M. Merigó | 2012 | Methods for strategic decision-making problems with immediate probabilities in intuitionistic fuzzy setting |
Para finalizar, es oportuno, presentar uno de los diversos ejemplos, bajo los cuales, en concreto, la lógica difusa ha hecho aportes en la teoría de la toma de decisiones.
Se considera la siguiente situación: (Kaufmann, A. y Gil Aluja, J., 1993)
Se debe seleccionar un candidato a un puesto de trabajo y, para ello, se ha determinado un conjunto de criterios a evaluar entre los posibles candidatos; dicho conjunto de criterios vendrá determinado por A={a, b, c, d, e, f}.
Se establece un nivel de competencia sobre A determinado por el conjunto borroso.

Es decir, los niveles esperados en el candidato seleccionado; dichos niveles vienen determinados por un valor entre 0 y 1 y son susceptibles de o, bien, ser medidos o ser cualificaciones de tipo subjetivo. En igual medida, la cualificación de un candidato debe expresarse como un conjunto borroso entre los mismos rangos.
Supongamos que se han presentado 5 candidatos y que bajo valoraciones para cada uno de ellos, se han podido establecer los siguientes conjuntos borrosos:
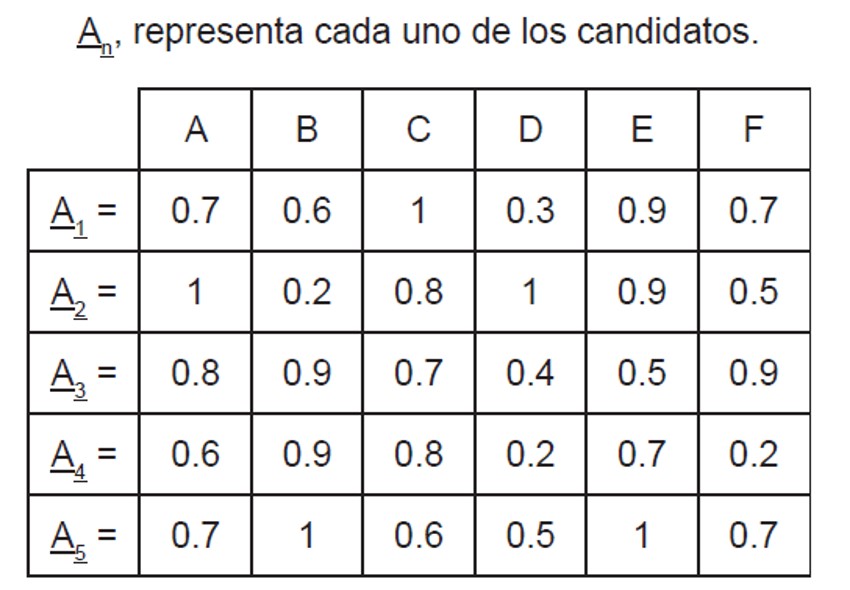
Se pretende determinar, a continuación, las diferencias entre las cualidades de los candidatos y el nivel de competencia establecido, entendido esto, como lo lejos o lo cerca que se encuentra un candidato, tanto de cada uno de los criterios de evaluación como del puesto de trabajo.
Para ello, es necesario comparar por pares los conjuntos establecidos, en particular, el conjunto que representa a cada candidato y el conjunto establecido como nivel de competencia. Por lo tanto, es pertinente considerar el concepto de distancia6 y, en particular, se escoge la distancia de Hamming, que permite determinar los aspectos en los que se diferencian dos conjuntos (borrosos o no).
Se considera, así, la distancia relativa de Hamming, es decir, el total de la distancia dividido entre seis (cardinal de A) entre cada An y C, lo cual, es equivalente a:
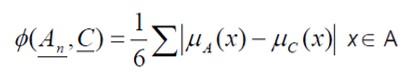
Recordemos, que 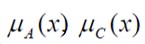 representan las funciones de pertenencia de cada
representan las funciones de pertenencia de cada 
Así, para cada candidato obtendremos:
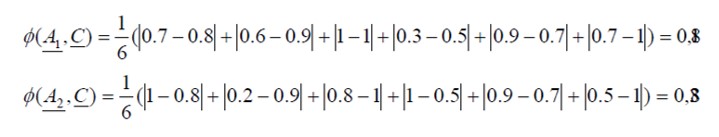
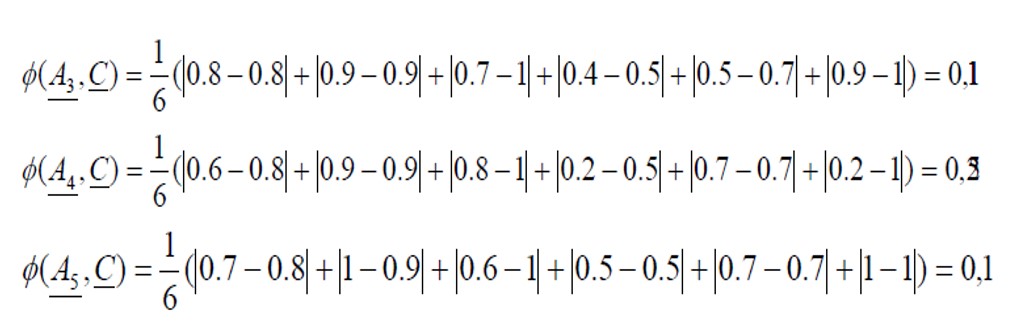
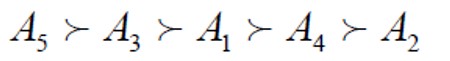 Obteniendo el siguiente orden entre candidatos:
Obteniendo el siguiente orden entre candidatos:
Determinando así, que el candidato más apto para el cargo es el representado por A5, según los criterios establecidos.
Conclusiones
1. El manejo de la posibilidad, de la ambigüedad, de lo incierto y de la subjetividad ha encontrado un sustento teórico matemático en la lógica difusa.
2. La lógica difusa permite el diseño de modelos capaces de incorporar la vaguedad, la ambigüedad asociada con el proceso de toma de decisiones en ambientes de incertidumbre.
3. Se abre un abanico de posibilidades, estudios futuros y nuevas herramientas frente a las metodologías para la toma de decisiones en cuanto al manejo de variables de tipo subjetivo, parcialmente desconocidas e inciertas; variables que no cuentan con una función de probabilidad subjetiva o no.
4. En las últimas décadas, el trabajo basado en los fundamentos de la lógica difusa se ha incrementado, ampliando las gamas de posibilidades a diversas áreas del conocimiento y dando nuevas herramientas al estudio de fenómenos poco trabajados desde las matemáticas, sobre todo, fenómenos propios de las ciencias sociales.
5. Existe una amplia gama de trabajos adelantados sobre la toma de decisiones empresariales con lógica difusa que sirven como apoyo a los administradores, economistas y contadores públicos en la planificación, desarrollo de estrategias y proyecciones financieras.
Bibliografía
Adams, T. (1994) Retaining structure selection with unequal fuzzy project-level objectives. J. Intell. Fuzzy Syst., 2 (3), 251–266.
Andronic, B. (2000). Applications of fuzzy sets in issues of economic decisions and analysis. Fuzzy economic review. 2(5).
Bellamn R. Zadeh L (1970). Decision-making in a fuzzy environment. Management science. 17(4). 141–164.
Bermúdez, J. Segura, J. Vercher, E. (2007). Modelos borrosos de optimización para la selección de carteras basados en intervalos de medias. Argentina: Red Cuadernos CIMBAGE. 9.
Bezdek, J., Spillman, B. and Spillman, R. (1978) A fuzzy relation space for group decision theory. Fuzzy Sets Syst., 1, 255–268.
Carrizo, M.A., Casparri, M.T. y Taboada, E. (2000). Una selección de canales de distribución a través de relaciones borrosas. Argentina: Red Cuadernos CIMBAGE. 3.
Carlsson, C. and Fullér, R. (1996). Fuzzy multiple criteria decision making: Recent developments, Fuzzy Sets and Systems, 78. 139-153. doi: 10.1016/0165- 0114(95)00165-4
Cebi. S, Kahraman, C. (2010). Fuzzy multicriteria Group decision making for real estate investments. Proceedings of the Institution of Mechanical Engineers. 224. 257-470.
Córdoba, M. (2004). Metodología para la toma de decisiones. Madrid, España: Delta.
Fedrizzi, M. (1995). Fuzzy approaches to modelling consensus in group decision support. Fuzzy economic review. 0.
García-Lapresta, J. Bonifacio Llamazares, B. (2003) Choosing a ranking of alternatives in a two-stage group decision procedure with individual linguistic assessments. Fuzzy economic review. 1 (8).
Gil Aluja, J. (1997) Nuevas técnicas de gestión de empresas. Retos empresariales para 1998. Ed. Estola Universitaria d’Estudis Empresariales (U.B.). España: Barcelona
Gil Aluja, J. (2005). La matemática borrosa en economía y gestión de empresas. Curso interuniversitario: sociedad ciencia tecnología y matemáticas 2005. Modulo I. 1-15. Recuperado de: http://imarrero.webs.ull.es/sctm05/modulo1tf/1/jgil.pdf
Gil Aluja, J (2009) Génesis de una teoría de la incertidumbre. España: Fundación General de la Universidad Autónoma de Madrid.
Gil Lafuente, J. (2006) Nuevo instrumento de selección: el “Índice de descartes por superación-distancia. Argentina: Red Cuadernos CIBAGE. 7
Gil Lafuente, A. (2004) Nuevas estrategias para el análisis financiero de la empresa. Argentina: Ariel.
Gutiérrez, I. Tellería, R. (2009) Un sistema basado en casos para la toma de decisiones en condiciones de incertidumbre. Revista Investigación Operacional. 2(23). Cuba: Editorial Universitaria.
Gómez, D. Montero de Juan, J (2006) Algunas aportaciones sobre representación de preferencias. España: Universidad Complutense de Madrid.
Gurokac, E. (1996). Fuzzy multiple criteria decision making for natural resource projects. Fuzzy economic review. 2(1).
Haage, C. (1978) Possibility and cost in decision analysis. Fuzzy Sets Syst., 1 (2), 81–86.
Herrera, E. Herrera-Viedma, and L. Martínez. (2000) A fusion approach for managing multi-granularity linguistic term sets in decision making. Fuzzy Sets and Systems, 114(1):43–58, August
Herrera, E. Herrera-Viedma, and F. Chiclana. (2001) Multiperson decision-making based on multiplicative preference relations. European Journal of Operational Research, 129(2):372–385, March.
Jablonowski, M. (1991) Fuzzy logic and insurance decisions, CPCU J. September 181–187.
Jain, R. (1976) Decision-making in the presence of fuzzy variables. IEEE Trans. Syst.,Man, Cybern., 6 (10), 698–703.
Jain, R. (1978) Decision-making in the Presence of Fuzziness and Uncertainty. Proceedings of the IEEE Conference on Decision Control, New Orleans, pp. 1318–1323.
Kaufmann, A. y Gil Aluja, J. (1993). Introducción de la teoría de los subconjuntos borrosos a la gestión de las empresas. (3ª. Edición). Santiago de Compostela, España: Milladoiro.
Kaufmann, A. Gil Aluja, J. y Terceño, A. (1993). Matemáticas para la economía y la gestión de empresas. Vigo, España: Foro científico.
Kleyle, R. de Korvin, A, McLaughlin, T. (1996). Decision making on the basis of expected cost variance: a fuzzy set approach. Managerial finance. (22)11.18-29.
Klir, G. Yuan, B. (1995). Fuzzy sets and Fuzzy logic. NJ, USA: Prentice Hall.
Lazzari, L. Machado, E. Pérez, R (1998) El metodo fuzzy - delphi. Estimación del cash - flow a través de la opinión de expertos. Argentina: Red Cuadernos CIMBAGE. 1.
Lazzari, L. Machado, E. Pérez, R (1998). Teoría de la decisión en condiciones de incertidumbre. Argentina: Red Cuadernos CIMBAGE. 1.
Lazzari, L. Machado, E. Pérez, R (1998). El problema de selección de personal. Argentina: Red Cuadernos CIMBAGE. 1.
Lazzari, L. Machado, E. (2001) Consideraciones acerca de los procesos de decisión híbridos. Argentina: Red Cuadernos CIMBAGE. 4.
Liu, Chin-Hung (2010). A group decision-making method with fuzzy set theory and genetic algorithms in quality function deployment. Qual Quant 44. 1175–1189.
Lunba, F. (2006). Modeling imprecision and subjectiveness for the multiattribute decisions. Fuzzy economic review. 1(11).
Maes, M. and Faber, M. (2004) Issues in utility modeling and rational decision making. Proceedings of 11th IFIP WG 7.5 Reliability and Optimization of Structural Systems (eds M. Maes and L. Huyse), Balkema Publishers, London, pp. 95–104.
Mallo, Paulino E.; Artola, María Antonia; Galante, Marcelo Javier; Martínez, Diego; Pascual, Mariano Enrique y Morettini, Mariano (2003). Aplicación del método delphi a las decisiones financieras en situaciones de incertidumbre. Jornadas de Profesores Universitarios de Matemática Financiera, 24, octubre 2003, Comodoro Rivadavia.
Mallo, Paulino E.; Artola, María Antonia; Galante, Marcelo Javier; Pascual, Mariano Enrique; Morettini, Mariano y Busetto, Adrián Raúl (2006). Aplicación de herramientas borrosas al balance scorecard. Costos y Gestión, 16 (61). pp. 12-19.
Mallo, Paulino E.; Artola, María Antonia y Morettini, Mariano (2009). Decisiones financieras con programación lineal: diferentes estados de la naturaleza. Jornadas Nacionales de Profesores Universitarios de Matemática Financiera, 30, 8-10 octubre 2009, Tucumán.
Morillas, A. Díaz, B. González, J. (1997) A fuzzy multiple attribute decision proposal for evaluating environmental plans. Fuzzy economic review. 1(2).
Nurmi, H (1981) Approaches to collective decision-making with fuzzy preference relations. Fuzzy Sets and Systems, 6 249-259.
Okuda, T., Tanaka, H., and Asai, K. (1974) Decision making and information in fuzzy events. Bull. Univ. Osaka Prefect., Ser. A, 23 (2), 193–202.
Okuda, T., Tanaka, H., and Asai, K. (1978) A formulation of fuzzy decision problems with fuzzy information, using probability measures of fuzzy events. Inf. Control , 38 (2), 135–147.
Peñalva Rosales, L. (2000). Propuesta de lógica difusa para la toma de decisiones. Politica y cultura. 13. 97-112.
Reig, J. Sansalvador, M. Trigueros, J. (200). La lógica borrosa y su aplicación a la contabilidad. Revista Española de Financiación y Contabilidad. XXIX. (103) 83-106.
Resnik, Michael D. (1987). An Introduction to Decision Theory. University of Minnesota Press.
Ross, T. (2004) Fuzzy Logic with Engineering Applications. NJ, USA: John Wilwy and Sons.
Sakawa, M. (1993) Fuzzy Sets and Interactive Multiobjective Optimization. New York: Plenum Press
Tanaka, H., Okuda, T., and Asai, K. (1976) A formulation of fuzzy decision problems and its application to an investment problem. Kybernetes, 5, 25–30.
Vasant, P. (2005). Fuzzy production planning and its application to decision making. Journal of Intelligent Manufacturing, 17, 5–12.
Wei, G. Merigó, J. (2012). Methods for strategic decision-making problems with immediate probabilities in intuitionistic fuzzy setting. Scientia Iranica. 19 (6), 1936–1946
Yager, (1978) Fuzzy decision-making including unequal objectives. Fuzzy Sets and Systems, 1. 87-95.
Yager, R. (1981) A new methodology for ordinal multiobjective decisions based on fuzzy sets. Decis. Sci., 12, 589–600.
Zadeh, L. (1975). Fuzzy Logic and Approximate Reasoning. Synthese, 30, 407-428
Zadeh, L. (1978). Fuzzy Sets as a Basis for a Theory of Possibility. Fuzzy Sets and Systems. 1, 3-28.
Zimmermann, J. (1978) Fuzzy Sets, decision-making and Expert Systems. Boston: Kluwer Academic Publisher.
Zimmermann, J. (1990) Decision-making in ill-structured environments and with multiple criteria. Bana e Costa ed., Readings in Multiple Criteria Decision Aid Springer Verlag, 119-151.
Zopounidis, C. Doumpos, M. (1997). A multicriteria method for sorting decisión problems under uncertainty. Fuzzy economic review. 1(2).
Notas

