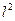Resumen: En el presente trabajo se caracterizan los espacios de Hilbert separables de dimensión infinita y se prueba que son isométricamente isomorfos al espacio de Hilbert l 2 .
Palabras clave: Espacio de Hilbert l 2 , bases ortonormales, espacios de Hilbert separables.
Abstract: In this paper separable Hilbert spaces of infinite dimension are characterized, and it is proven that they are isometrically isomorphic to the Hilbert space l 2 .
Keywords: Hilbert space l 2, orthonormal bases, separable Hilbert spaces.
Caracterización de los espacios de Hilbert separables
Characterization of Hilbert’s separable spaces.
Recepción: 01 Marzo 2018
Aprobación: 10 Mayo 2018
Un importante espacio de Hilbert, que recuerda en su aspecto al espacio de coordenadas de dimensión infinita, es el espacio de todas las sucesiones
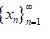
números reales o complejos para las que
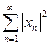
converge. Este es el espacio de Hilbert
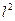
el cual es el prototipo de los espacios de Hilbert separables de dimensión infinita.
En este trabajo se revisan las propiedades de las bases ortonormales en los espacios de Hilbert y se caracterizan los espacios de Hilbert separables de dimensión infinita se prueba que
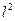
es isométricamente isomorfo a cualquier espacio de Hilbert separable dimensión infinita.
Sean
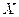
un espacio con producto interno y
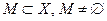
.
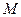
es un conjunto ortonormal si
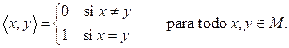
Todo conjunto ortonormal
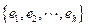
en un espacio con
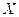
es linealmente independiente. En particular, si
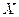
es
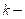
dimensional entonces elconjunto
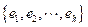
es una base para
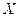
y cualquier vecto
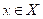
puede ser expresado en la forma
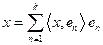
(en este caso
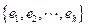
usualmente se llama base ortonormal y los números
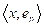
son las componentes de
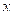
base, los cuales son llamados los coeficientes de Fourier de
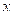
con respecto a esta base ortonormal).
Sea
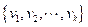
un subconjunto linealmente independiente de un espacio con producto interno
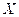
y sea
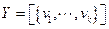
Entonces existe una base ortonormal
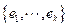
para
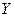
Sea
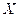
un espacio con producto interno. Una sucesión
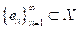
dice que es una sucesión ortonormal si
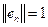
para todo
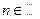
, y
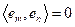
para todo

con
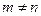
; es decir,
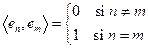
Todo espacio con producto interno
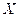
de dimensión infinita contiene una sucesión ortonormal.
Sea
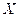
un espacio con producto interno y sea
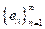
una sucesión ortonormal en
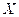
. Para cualquier
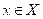
la serie (real)
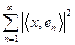
converge y
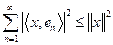
Sean
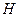
un espacio de Hilbert y
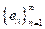
una sucesión ortonormal en
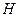
Sea
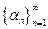
una sucesión en
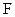
. Entonces, la serie
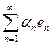
converge en
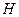
si y solo si la serie
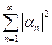
converge en
. Si este es el caso, entonces
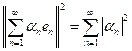
Sea
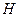
un espacio de Hilbert y sea
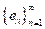
una sucesión ortonormal en
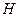
.Para cualquier
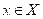
la serie
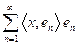
en converge en
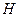
Sean
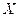
un espacio con producto interno y
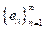
una sucesión ortonormal en
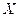
. Entonces para cada
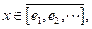
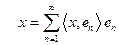
Sea
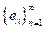
una sucesión ortonormal en el espacio de Hilbert
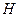
. Los siguientes enunciados son equivalentes:
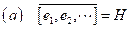
; es decir, el subespacio generado por el conjunto ortonormal
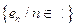
es denso en
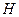
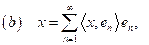
para todo
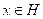
; es decir, todo elemento de
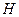
es igual a su serie de Fourier.
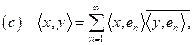
para todo
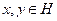
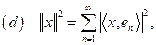
, para todo
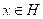
. Identidad de Parseval.
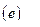
No existe un conjunto ortonormal en
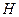
que contiene propiamente al conjunto
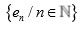
.O sea que
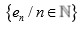
es maximal en el sentido ortonormal.
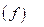
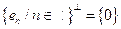
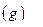
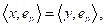
para todo
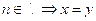
Sea
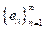
una sucesión ortonormal en el espacio de Hilbert
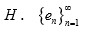
es una base ortonormal para H si se satisface una de las condiciones de la Propiedad
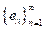
es una sucesión ortonormal total o completa.
Ahora que se han estudiado las bases ortonormales en detalle, es natural preguntarse qué espacios de Hilbert poseen una base ortonormal.
Un espacio de Hilbert
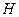
se llama separable si existe una familia enumerable de vectores
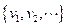
tal que
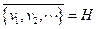
Todo espacio de Hilbert de dimensión finita es separable.
Demostración: Sea
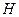
un espacio de Hilbert tal que
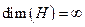
y sea
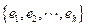
una base para
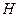
. Definamos,
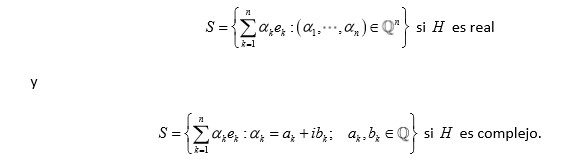
En cualquier caso
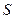
es enumerable y
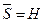
. Por lo tanto,
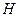
es separable.
El siguiente Teorema caracteriza a los espacios de Hilbert separables de dimensión
infinita.
Un espacio de Hilbert de dimensión infinita
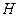
es separable si y solo si posee una base ortonormal.
Demostración:

por construcción
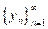
es un conjunto linealmente independiente y
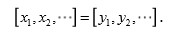
Por el proceso de Gram-Schmidt podemos construir una sucesión ortonormal
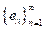
tal que
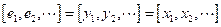
Por lo tanto,
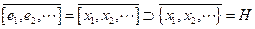
Así pues,
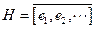
con
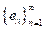
una sucesión ortornormal, de donde
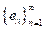
es una base ortonormal para
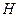
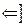
Supongamos ahora que
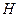
posee una base ortonormal
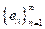
Luego para todo
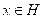
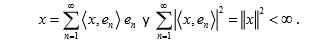
Sea
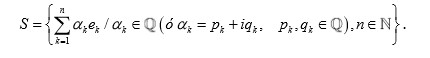
Luego,
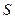
es un conjunto enumerable. Probemos que
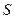
es denso en
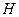
. Sea
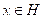
, entonces
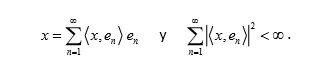
Sea
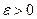
entonces existe un
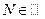
Tal que
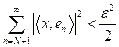
Para cada
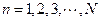
tomemos
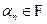
racional o complejo racional (según sea el caso ) tal que
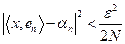
Tomemos
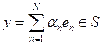
entonces
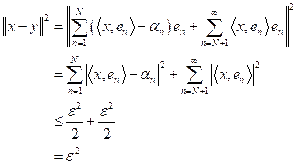
de donde
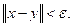
Esto implica que
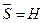
y por lo tanto,
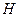
es separable.
La sucesión ortonormal
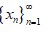
es una base ortonormal para
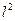
donde
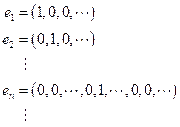
Demostración: Es claro que para cualquier
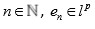
para todo
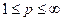
Note que
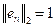
para todo
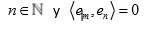
para todo
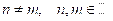
. Así,
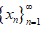
es, en efecto, una sucesión ortonormal en
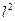
Por otro lado, sea
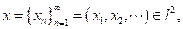
entonces
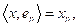
por lo tanto,
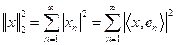
O sea, se satisface la identidad de Parseval. Por lo tanto,
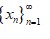
es una base ortonormal para
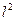
(Por la Definición 2.11).
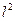
es separable.
Demostración: Se deduce directamente de los Teoremas 3.3 y 3.4.
Sean
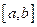
un intervalo acotado y
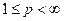
. Entonces el conjunto
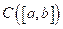
es denso en
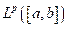
Para cualquier
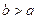
el conjunto de polinomios con coeficientes racionales ( o complejos racionales ) es denso en el espacio
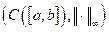
Demostración: Consideremos el espacio
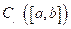
, con la norma
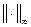
, y supongamos

Entonces
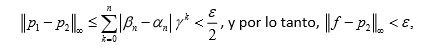
lo que demuestra el resultado.
Para el caso complejo aplicamos este resultado a la parte real e imaginaria de
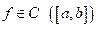
Para cualquier
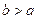
el conjunto de polinomios con coeficientes racionales
(o complejos racionales) es denso en el espacio
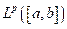
Demostración: Consideremos el espacio
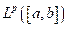
, con la norma
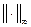
y supongamos que

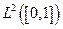
es separable.
Demostración: El conjunto de polinomios con coeficientes racionales (o complejos racionales) es enumerable y denso en
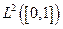
. Por lo tanto,
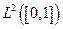
es separable.
Sean
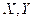
espacios normados y
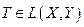
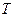
es una isometría si
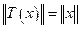
para todo
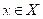
. Si T es una isometría suryectiva, entonces se dice que
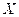
y
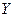
son espacios normados isométricamente isomorfos.
Sea
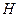
un espacio de Hilbert con una base ortonormal
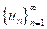
, entonces una isometría suryectiva
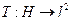
tal que
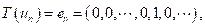
para todo
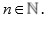
Demostración: Sea
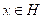
, entonces
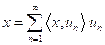

Sean
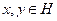
y
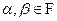
. Entonces
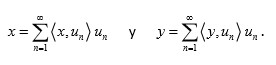
Luego,
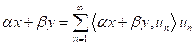
y
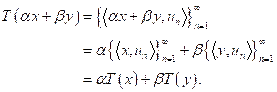
Por lo tanto,
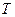
es lineal. Probemos que
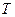
es una isometría. En efecto, por la identidad de Parseval se tiene que
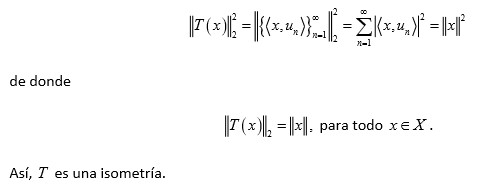
Probemos que
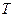
es suryectiva.

Todo espacio de Hilbert
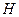
separable de dimensión infinita es
isométricamente isomorfo a
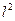
; es decir, existe una isometría
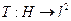
tal que es un isomorfismo.
Demostración: Como
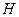
es un espacio de Hilbert separable de dimensión infinita entonces por el Teorema 3.3,
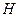
posee una base ortonormal y, por el Teorema 3.11,
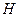
es isométricamente isomorfo a
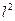
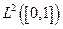
es isométricamente isomorfo a
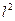
Demostración: Por el Corolario 3.9
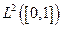
es un espacio de Hilbert separable de
dimensión infinita, luego por el Corolario 3.12
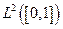
es isométricamente isomorfo a