



Ensino de Matemática, Diversas Possibilidades
Resolução de Problemas: explorando suas potencialidades a partir de um projeto de intervenção envolvendo a matemática financeira
Problem solving: exploring its potential from an intervention project involving financial mathematics
Resolución de problemas: exploración de su potencial a partir de un proyecto de intervención que involucra matemáticas financieras
Revista de Educação Matemática
Sociedade Brasileira de Educação Matemática, Brasil
ISSN: 2526-9062
ISSN-e: 1676-8868
Periodicidade: Cuatrimestral
vol. 18, e021020, 2021
Recepção: 09 Novembro 2020
Aprovação: 05 Abril 2021
Publicado: 07 Abril 2021

Resumo: Este artigo busca explorar, a partir de uma experiência prática envolvendo conteúdos de matemática financeira, o uso da Resolução de Problemas enquanto metodologia para o Ensino de Matemática. Para isso, desenvolvemos uma pesquisa de campo a partir de um projeto de intervenção pedagógica executado em uma turma de primeiro ano do Ensino Médio de um colégio estadual do município de Aiquara-BA. As atividades que constituíram o núcleo do projeto de intervenção foram elaboradas à luz das pesquisas de Polya (1995) e Onuchic (1999), os quais serviram de referencial teórico-metodológicos. O tema selecionado para as atividades envolveu os conceitos de porcentagem e de juros. A partir da análise dos problemas trabalhados pelos estudantes e das observações do professor regente durante as atividades, um conjunto de dados foi organizado. Avaliando-os, foi possível identificar que a utilização da Resolução de Problemas como metodologia de ensino contribuiu para o desenvolvimento de diferentes aspectos do processo de ensino-aprendizagem, como o raciocínio lógico, a capacidade argumentativa e o trabalho em equipe. Além disso, constatamos uma mobilização mais efetiva dos conhecimentos prévios dos estudantes e de suas percepções a respeito dos potenciais de utilização dos conteúdos trabalhados em situações cotidianas práticas. Esperamos com isso poder contribuir para uma melhor compreensão dos potenciais envolvidos no ensino de matemática através da Resolução de Problemas.
Palavras-chave: Resolução de Problemas, Matemática Financeira, Metodologia de ensino.
Abstract: This article seeks to explore, from a practical experience involving financial mathematics content and the use of Problem Solving as a methodology for Teaching Mathematics. To this end, we developed a field research based on a pedagogical intervention project carried out in a first-year high school class at a state school in the municipality of Aiquara-BA. The activities that constituted the core of the intervention project were elaborated in the light of research by Polya (1995) and Onuchic (1999), which served as a theoretical and methodological framework. The theme selected for the activities involved the concepts of percentage and interest. From the analysis of the problems worked by the students and the observations of the conducting teacher during the activities, a data set was organized. Evaluating them, it was possible to identify that the use of Problem Solving as a teaching methodology contributed to the development of different aspects of the teaching-learning process, such as logical reasoning, argumentative capacity, teamwork. In addition, we found a more effective mobilization of students' prior knowledge and their perceptions regarding the potential for using the content worked in practical everyday situations. We hope that with this we can contribute to a better understanding of the potentials involved in teaching mathematics through Problem Solving.
Keywords: Problem solving, Financial math, teaching methodology.
Resumen: Este artículo busca explorar, desde una experiencia práctica involucrando contenidos de matemáticas financieras y el uso de la Resolución de Problemas mientras metodología para la Enseñanza de las Matemáticas. Para esto, desarrollamos una investigación de campo a partir de un proyecto de intervención pedagógica ejecutado en una clase de primer año Enseñanza Secundaria en una escuela pública de la ciudad de Aiquara-BA. Las actividades que constituyeron el núcleo del proyecto de intervención fueron elaboradas a la luz de las investigaciones de Polya (1995) y Onuchic (1999), que sirvieron como referenciales teóricos y metodológicos. El tema seleccionado para las actividades involucró los conceptos de porcentaje e interés. A partir del análisis de los problemas trabajados por los estudiantes y las observaciones del profesor regente durante las actividades, se organizó un conjunto de datos. Evaluándolos, se pudo identificar que el uso de la Resolución de Problemas como metodología de enseñanza contribuyó el desarrollo de diferentes aspectos del proceso de enseñanza-aprendizaje, tales como el razonamiento lógico, la capacidad argumentativa, el trabajo en equipo. Además, encontramos una movilización más efectiva de los conocimientos previos de los estudiantes y de sus percepciones sobre el potencial de utilización de los contenidos trabajados en cotidianas prácticas. Esperamos que con esto contribuir para una mejor comprensión de los potenciales involucrados en la enseñanza de las matemáticas através de la Resolución de Problemas.
Palabras clave: Resolución de problemas, Matemáticas Financieras, Metodología de Enseñanza.
1. Introdução
A Resolução de Problemas (RP) enquanto metodologia de ensino constitui uma das importantes tendências contemporâneas no Ensino da Matemática. Tal fato é amparado por uma série de pesquisas que envolvem tanto reflexões teóricas como pesquisas empíricas. Em ambos os casos, um amplo espectro de contextos de ensino e diferentes aspectos do processo de ensino-aprendizagem têm sido considerados (ONUCHIC, 2011, ONUCHIC et al, 2014).
No presente artigo, que possui um caráter empírico e qualitativo, pretendemos explorar os potenciais que a RP pode oferecer para o Ensino da Matemática em um contexto específico do primeiro ano do Ensino Médio de uma escola pública no interior da Bahia. O tema escolhido para se trabalhar através da RP foi a Matemática Financeira, em particular os conceitos de porcentagem e de juros.
Segundo Coutinho e Silva (2016), a Matemática Financeira ainda apresenta índices deficitários de aprendizagem. Em suas pesquisas eles articulam o uso “resolução de problemas” e de “mídias tecnológicas” com o intuito de criar ambientes dinâmicos e favoráveis à aprendizagem. Buscam assim estabelecer conexões entre a teoria e a prática, relacionando o cálculo de porcentagem e juros com cotidiano dos estudantes e com a sociedade. Com isso, defendem que é possível contribuir para formação de cidadãos críticos e consumidores conscientes, capazes de analisar e compreender dados e informações envolvendo o cálculo de porcentagens e de juros, bem como administrar de forma coerente seus recursos financeiros.
Inspirados pelos desafios deste tema e pelo objetivo acima mencionado, a questão que investigamos nesta pesquisa foi formulada nos seguintes termos: Quais as possibilidades que emergem no processo de ensino-aprendizagem ao se trabalhar os conceitos da matemática financeira através da RP? Mais especificamente, tal questão pretende ser considerada em um contexto como o que identificamos na escola acima referida, com um público-alvo formado por estudantes que apesar de obterem notas para aprovação na disciplina de Matemática a consideram como uma das mais difíceis do currículo e demonstram uma baixa motivação e um fraco envolvimento em suas aulas.
Assim, partimos da hipótese de que através da RP um conjunto de aspectos pedagógicos importantes para o desenvolvimento intelectual, social e motivacional dos estudantes poderiam ser estimulados. Em particular, consideramos nesta pesquisa os seguintes aspectos: o protagonismo dos estudantes no estabelecimento de estratégias para a resolução de problemas, a mobilização de seus conhecimentos prévios, o trabalho em equipe, o raciocínio lógico e as habilidades de interpretação, argumentação e reflexão, entre outros.
Desta forma, acreditamos que as dificuldades impostas pelo contexto anteriormente mencionado podem encontrar alternativas de superação pedagogicamente viáveis e enriquecedoras. Com isso em mente, um projeto de intervenção pedagógica envolvendo a RP aplicada à Matemática Financeira foi elaborado, tomando como referência os preceitos defendidos por Polya (1995) e os caminhos apontados por Allevatto e Onuchic (2014).
No que se segue, faremos uma revisão mais aprofundada da literatura sobre a RP enquanto metodologia de ensino e, nas seções subsequentes, descreveremos a metodologia e os procedimentos utilizados na pesquisa, seguidos da apresentação dos dados e discussão. Por fim, teceremos nossas considerações finais.
2. Revisão de Literatura
De acordo com Onuchic e Allevatto (2011), a RP ganha importância para o ensino de matemática em 1945 com a publicação do livro How to Solve It (traduzido para o português como A Arte de Resolver Problemas) de George Polya. Nele, o autor enfatizava que:
Resolver problemas é uma habilidade prática como, digamos, o é a natação. Adquirimos qualquer habilitação por imitação e prática. Ao tentarmos nadar, imitamos o que os outros fazem com as mãos e os pés para manterem suas cabeças fora d’água e, afinal, aprendemos a nadar pela prática da natação. Ao tentarmos resolver problemas, temos de observar e imitar o que fazem outras pessoas quando resolvem os seus e, por fim, aprendemos a resolver problemas, resolvendo-os (POLYA, 1995, p.3).
Contudo, os estudos apresentados por Polya foram largamente secundarizados com a advento do Movimento da Matemática Moderna, que vigorou entre o final da década de 1950 e fins dos anos de 1970. Este movimento priorizava o ensino das estruturas lógicas, algébricas, topológicas e de ordem, enfatizando a teoria dos conjuntos. Já sua abordagem pedagógica voltava-se para a estrutura da disciplina, realçando uma linguagem matemática universal, com uso de símbolos e terminologia complexa, dando um caráter formal ao ensino e distanciando-se das questões práticas (ONUCHIC, 1999).
Algumas pesquisas identificam a RP em perspectiva histórica, tais como Amaral, Sant’Ana, Sant’Ana (2019) que apresentam a reflexão sobre um manual de ensino primário, refletindo sobre o programa escolar dos anos de 1930 e Santos, Dynnikov, Sant’ana, Fernandes, Sant’ana, (2016) apresentam uma análise da RP difundidas nas revistas que circularam no Brasil no período compreendido entre de 1890 e 1970.
Na década de 1980, educadores de diversos países passaram a revisitar a RP enquanto metodologia de ensino. Em particular, a partir da publicação, nos Estados Unidos, de documentos[4] em apoio à RP, a mesma passou a ser acolhida de forma mais efetiva no ensino escolar. (ONUCHIC; ALLEVATTO, 2011).
De uma forma geral, o ensino através da RP propõe que o estudante atue como ser ativo no processo de aprendizagem dos conceitos matemáticos. O professor, como mediador, deve apresentar um problema que instigue o estudante a mobilizar conceitos aprendidos e propor estratégias para sua resolução. De acordo Diniz (2001, p. 89), a RP deve estimular “situações que não possuem solução evidente e que exigem que o resolvedor combine seus conhecimentos e decida pela maneira de usá-los em busca da solução”. Frente a esse posicionamento, a autora entende que a RP vai além de uma metodologia ou conjunto de orientações didáticas, considerando-a como uma “perspectiva metodológica” (DINIZ, 2001, p. 87), maneira de organizar o ensino em sua plenitude, para além das metodologias, envolve a necessidade de se ter concepções sobre o ensinar e o aprender.
Já para Onuchic (2008, p.7), a RP
passa a ser pensada, então, como uma metodologia de ensino, como um ponto de partida e um meio de se ensinar matemática. Essa forma de ensinar Matemática passa a ser vista como um modelo “Pós Polya”. Não se aboliam as heurísticas nem a exigência de os alunos “pensarem” de Polya. Mas, o ensino, que até então era centrado no professor, passava a ser centrado no aluno.
Cabe salientar, conforme aponta a autora, que o processo de disseminação da RP enquanto metodologia de ensino precisou, nos anos de 1980 e 1990, adentrar os cursos de formação de professores. Estes, por sua vez, precisaram compreender sua fundamentação e seus preceitos, uma vez que era necessário compreendê-la como uma metodologia baseada na resolução de problemas como meio de aprendizado da matemática e não como um caminho para resolver um problema. A RP, mesmo tendo seu auge nos idos das décadas de 1980 e 1990, continua sendo uma temática de desenvolvimento de pesquisas, conforme podemos verificar desenvolvimentos recentes, por exemplo González (2020), Santos (2020), Silveira e Andrade (2020), Lima e Galvão (2020), Possamai e Silva (2020) e Lima (2020).
É muito comum encontrar as sugestões de Polya (1995, p. 3-4) apresentadas e discutidas em pesquisas relacionadas com a RP, as mais conhecidas etapas: (i) compreender o problema, (ii) estabelecer um plano, (iii) executar o plano e (iv) rever a execução. Na primeira etapa (i), o resolvedor vai olhar os dados do problema para entendê-lo, identificando a incógnita e atentar-se para os elementos desconhecidos. Em (ii), é preciso focar na incógnita e relacionar com outras situações semelhantes, direcionando possíveis caminhos para a solução, é a fase de elaboração de um plano estratégico. Na etapa (iii) deve executar o plano para a resolução do problema (seguindo cada passo) e por fim, em (iv) examinar a solução obtida, verificando os argumentos.
Nesse sentido, Van de Walle (2009, p.57) refere-se ao problema como “qualquer tarefa ou atividade na qual os estudantes não tenham nenhum método ou regra já receitados ou memorizados, nem que haja nenhuma percepção por parte do estudante de que exista um método “correto” específico de solução."
A definição exposta por Van de Walle (2009) diferencia uma dicotomia existente na prática pedagógica do professor de matemática no que se refere a problema e exercício. Entendendo que o exercício implica no fato de que quem o resolve deve ter conhecimentos suficientes para resolvê-los, e nem sempre exige reflexão aprofundada. Nesse sentido, o exercício configura uma atividade de treino com utilização de habilidade ou conhecimento matemático adquirido anteriormente, enquanto m problema refere-se a uma situação desafiadora que exige reflexão e tomada de decisões.
Meneghelli, Cardozo, Possamai e Silva (2018), refletiram sobre a utilização da metodologia de resolução de problemas no contexto escolar, resgatando algumas concepções históricas e estabelecendo uma relação com o Movimento da Matemática Moderna e apontam diferenças entre exercício, questão contextualizada e ainda um problema. Nesta perspectiva utilizam a RP desenvolvendo atividades para estudantes da 2ª série do Ensino Médio focando nos conceitos da Geometria Espacial. Como resultado de sua pesquisa apontaram que a utilização da RP constitui uma estratégia significante, pois viabiliza a aproximação dos conceitos matemáticos com o mundo real dos estudantes, além de possibilitar que eles participem da construção dos conceitos matemáticos.
No entanto, Nunes e Vidal (2017), ao focarem no trabalho com a RP como Metodologia de Ensino-aprendizagem-avaliação, na formação inicial de professores, entendem que a Formulação de Problemas e a Resolução de Problemas, pode ser um potencializador do processo de aprendizagem, com estímulo da assimilação dos conteúdos habilidades de resolução de problemas pela criatividade dos participantes.
Por fim, observamos que nos Parâmetros Curriculares Nacionais (PCN,1988), a RP é apresentada como eixo articulador para o conhecimento do estudante e os conhecimentos específicos. Na atualidade, a Base Nacional Comum Curricular (2017) faz várias referências ao termo resolução de problemas em diversas partes do documento. No que se refere a RP enquanto metodologia de ensino o documento alude que:
Os processos matemáticos de resolução de problemas, de investigação, de desenvolvimento de projetos e da modelagem podem ser citados como formas privilegiadas da atividade matemática, motivo pelo qual são, ao mesmo tempo, objeto e estratégia para a aprendizagem ao longo de todo o Ensino Fundamental. Esses processos de aprendizagem são potencialmente ricos para o desenvolvimento de competências fundamentais para o letramento matemático (raciocínio, representação, comunicação e argumentação) e para o desenvolvimento do pensamento computacional. (BRASIL, 2017, p. 266).
Vale destacar que as referências à RP no documento estão associadas à orientação de um ensino da matemática através da RP e também como processo de aplicação dos conhecimentos previamente adquiridos pelos estudantes.
3. Metodologia
Metodologicamente, o presente trabalho caracteriza-se como uma pesquisa de campo qualitativa, onde buscou-se descrever, compreender e explicar um determinado fenômeno. De acordo com Minayo (2011, p. 14) “a pesquisa qualitativa trabalha com o universo de significados, motivos, aspirações, crenças, valores e atitudes, o que corresponde a um espaço mais profundo das relações, dos processos e dos fenômenos que não podem ser reduzidos à operacionalização de variáveis”. Este tipo de pesquisa leva em consideração as diferenças entre o mundo social e o mundo natural, respeitando a relação existente entre os objetivos propostos pelos investigadores, suas orientações teóricas e seus dados empíricos.
Pesquisas dessa natureza “buscam explicar o porquê das coisas, exprimindo o que convém ser feito, mas não quantificam os valores e as trocas simbólicas nem se submetem à prova de fatos, pois os dados analisados são não-métricos e se valem de diferentes abordagens” (GERHARDT; SILVEIRA, 2009, p. 32).
Enquanto pesquisa de campo, “o objeto/fonte é abordado em seu meio ambiente próprio. A coleta de dados é feita nas condições naturais que os fenômenos ocorrem” (SEVERINO, 2017, p.122), possibilitando ao pesquisador coletar dados empíricos por meio de diversas fontes.
Assim, o trabalho se fundamenta a partir da obtenção, exposição e análise de um conjunto de informações relativas à implementação do projeto de intervenção pedagógica, o qual ocorreu no seu ambiente natural, a sala de aula.
No que se refere à obtenção do conjunto de informações por nós considerada, diferentes recursos foram utilizados, como a observação do pesquisador, os materiais e as atividades produzidas pelos estudantes ao longo das etapas da intervenção, assim como os diálogos estabelecidos entre os envolvidos (estudantes e professor).
Para uma contextualização do ambiente e do momento pedagógico/curricular para o qual o projeto foi pensado, cabe registrar que o mesmo teve como público-alvo uma turma de 35 estudantes de primeiro ano do Ensino Médio de uma Escola pública da cidade de Aiquara, interior da Bahia.
A elaboração do projeto de intervenção se deu no âmbito das atividades de Estágio Supervisionado do primeiro autor, enquanto licenciando do curso de Licenciatura em Matemática na Universidade Estadual da Bahia, Campus de Jequié-BA, e ocorreu no início do terceiro bimestre do ano de 2016 e foi estruturado em 4 momentos, a saber,
1º momento: Observação (04 aulas, de 50 min. cada);
2º momento: Conversa com o professor e estudantes;
3º momento: Abordagem da Resolução de Problemas enquanto estratégia de ensino (02 aulas de 50 min. cada);
4º momento: Discussão e sistematização do conteúdo abordado (02 aulas de 50 min cada).
O primeiro contato com a turma ocorreu no período de observação do ambiente escolar. Nesse momento, a professora responsável pela turma trabalhava o conteúdo de Progressão Aritmética. A partir das primeiras observações foi possível perceber que a turma se mostrava concentrada frente as aulas expositivas da professora, a qual sempre perguntava se os estudantes estavam entendendo e, por vezes, oferecia uma segunda explicação.
Nas aulas observadas, a professora seguia uma abordagem “tradicional” dos conteúdos, apresentando definição, exemplos, exercício e correção. Sempre com o suporte do livro de didático.
Durante esta etapa foi possível estabelecer uma relação dialógica com os estudantes, fazendo-lhes questionamentos sobre a disciplina. Nesse diálogo, constatamos a visão dos mesmos sobre as dificuldades que tinham com a disciplina de Matemática. Alguns relataram que essa era uma das que odiavam e outros acrescentaram que estavam com notas baixas.
Nos diálogos estabelecidos com a professora, constatamos que ela não tinha formação específica em Matemática. Ela confirmou os relatos dos estudantes quanto a dificuldade na disciplina, porém acrescentou que, apesar das dificuldades, a turma conseguia atingir a média para aprovação. Mencionou também que o comportamento deles nas aulas era sempre com pouca participação, mas que prestavam bastante atenção. Durante as conversas com a professora sobre o diagnóstico da turma e detalhes do projeto interventivo, ela sugeriu que o projeto abordasse o tema de Matemática Financeira, uma vez que a temática já constava do seu planejamento e ainda não tinha conseguido abordar o conteúdo.
A elaboração do projeto considerou os preceitos apresentados na seção anterior relativos à RP enquanto metodologia de ensino, tomando como referência a perspectiva de Onuchic (1999), a qual considera a RP uma orientação para a aprendizagem e não como uma atividade para ser desenvolvida em paralelo. Para ela,
O ponto de partida das atividades matemáticas não é a definição [de um conceito] mas o problema [a ele associado]; que o problema não é um exercício no qual o aluno aplica, de forma quase mecânica, uma fórmula ou uma determinada técnica operatória [...] mas constrói um campo de conceitos que tornam sentido num campo de problemas (ONUCHIC, 1999, p. 215).
Dentre os conteúdos relacionados a Matemática Financeira, optou-se por trabalhar os conceitos de porcentagem e de juros. A abordagem foi planejada para aplicação no segundo momento do projeto, o qual foi estruturado a partir da discussão dos seguintes problemas geradores, extraídos da apostila de Matemática Básica, do curso de Assistente Administrativo do SENAI (2015, p. 75):
1. Uma bicicleta, cujo preço é R$ 1200,00, pode ser comprada da seguinte maneira:
a) a vista, com 15% de desconto.
b) pagamento para 90 dias, com acréscimo de 25% sobre o preço inicial.
Responda: Qual é a diferença, em reais, entre as duas opções de compra?
2. A Confederação Brasileira de Futebol resolveu distribuir prêmios num total de R$ 640.000,00 para os quatro jogadores brasileiros que tiveram o melhor desempenho no ataque durante a Copa do Mundo. O critério adotado foi premiar aqueles que fizeram o maior número de gols, conforme o número de gols marcados por cada jogador. Os jogadores selecionados foram os que fizeram 9, 6, 3 e 2 gols. Nessas condições responda:
a) Quanto recebeu cada jogador?
b) Qual taxa de porcentagem que esses valores representam?
Cabe aqui ressaltar o cuidado que o professor deve ter com a escolha/elaboração do problema, o qual deve estar atrelado a um objetivo estreitamente vinculado à prática pedagógica, onde o estudante possa recorrer a múltiplas estratégias de aprendizagem.
Sobre a sua formulação, Schoenfeld (1996, p. 68-69) aponta algumas características que devem ser visadas na elaboração do problema, a saber,
(a) devem ser acessíveis e facilmente compreendidos, sem um vocabulário desconhecido da maioria dos alunos; (b) devem poder ser resolvidos de diversas maneiras e oferecer múltiplas soluções, valorizando não a resposta, mas as conexões; (c) devem servir, assim como suas soluções, para a introdução de ideias matemáticas importantes; e (d) devem, se possível, ser como “germens para ‘honestas e boas’ explorações matemáticas”.
Para a execução da sequência de problemas, foi solicitado à turma a constituição de grupos entre os presentes. Cinco grupos contendo sete estudantes foram formados. Cada um recebeu uma cópia dos problemas geradores a serem resolvidos. Foi então solicitada a leitura individual e silenciosa dos problemas. Nesse momento, alguns já questionaram o modo de resolução das questões e o professor regente orientou-os à luz dos princípios apresentados por Allevatto e Onuchic (2014, p. 44-46) relativos à elaboração de um roteiro sequencial de atividades pautados pela RP, a saber:
1. Proposição do problema – Selecionar ou elaborar um problema e denominando-o de problema gerador.
2. Leitura individual – Distribuir uma cópia impressa do problema para cada aluno e solicitar a leitura do mesmo.
3. Leitura em conjunto – Distribuir a turma em pequenos grupos e, solicitar uma nova leitura do problema.
4. Resolução do problema - A partir do momento em que o aluno estudante entendeu o problema e tenta resolvê-lo, em grupo, permitindo assim a construção de conhecimento sobre o conteúdo que o professor planejou para aquela aula.
5. Observar e incentivar – Nesse momento, o professor muda de comunicador do conhecimento para o de observador, organizador, consultor, mediador, interventor, controlador, incentivador da aprendizagem.
6. Registro das resoluções na lousa - Anotam-se os resultados obtidos pelos grupos quer sejam certos ou errados e aqueles feitos por diferentes caminhos.
7. Plenária – Assembleia com todos os alunos. Como todos trabalham sobre o problema dado, estão ansiosos quanto a seus resultados, dessa forma, participam.
8. Busca do consenso – Após discussões e sanadas as dúvidas, o professor juntamente com os alunos tentam chegar a um consenso.
9. Formalização do conteúdo – Faz-se uma síntese daquilo que se objetivava “aprender” a partir do problema gerador. São colocadas as devidas definições, identificando propriedades, fazendo demonstrações, etc.
10. Proposição e resolução de novos problemas – Nesta etapa, após a formalização do conteúdo, propõem-se novos problemas para fixação de aprendizagem.
Assim, foi informando aos estudantes que cada grupo escolheria a melhor estratégia para resolução dos problemas, orientado que fizessem a leitura silenciosa e observassem o que o problema solicitava. Em seguida, uma leitura coletiva em voz audível foi efetuada e um tempo para resolução foi estabelecido. Inicialmente foi estipulado o tempo de quarenta minutos para resolução, outros vinte minutos foram reservados para a socialização da resolução no quadro e, por fim, a sistematização do conteúdo.
No entanto, foi possível perceber a dificuldade para encontrar uma estratégia para resolução dos problemas. Nos primeiros instantes, perguntavam qual seria a solução e quais os passos para chegar a mesma. Se o assunto não seria explicado para facilitar a solução do problema.
Em alguns grupos, o professor foi mediando e explicando mais uma vez que cada um teria autonomia para chegar ao resultado, independente da forma que seria explicado nas aulas seguintes. Esta atuação do professor nos grupos é preconizada por Allevatto e Onuchic (2014) direcionando para a supervisão, verificando se os estudantes compreenderam o problema. Caso necessitem de orientação, o professor deve fornecê-la para que a tarefa fique clara, sem, no entanto, explicar como resolver o problema.
Devido a este procedimento, o período oferecido precisou ser estendido para além dos quarenta minutos estabelecido inicialmente, onde obtivemos a constatação:
| Quadro 1: levantamento das questões respondidas | |||
| Grupos | Questão 1 | Questão 2 | Total de acerto |
| Grupo 1 | Respondeu | Respondeu | 01 |
| Grupo 2 | Respondeu | Tentou responder | 01 |
| Grupo 3 | Respondeu | Não respondeu | 01 |
| Grupo 4 | Respondeu | Não respondeu | 01 |
| Grupo 5 | Respondeu | Não respondeu | 00 |
Como se nota, dos cinco grupos apenas um conseguiu responder às duas questões, porém a segunda questão apresentada ofereceu uma solução incorreta; o grupo dois respondeu a primeira questão correta, esboçou responder a segunda, mas não prosseguiu; outros dois grupos responderam apenas a primeira questão corretamente e um tentou responder a primeira questão, porém a solução estava errada.
4. Resultados
Nesta seção analisaremos de forma detalhada os resultados obtidos através da correção dos problemas. A percepção do professor regente sobre o desenvolvimento das atividades também será considerada. No que se refere ao problema gerador 1, analisando a solução do item “a”, foi constatado que no grupo 01 a resolução se deu através da regra de três (Figura 1).
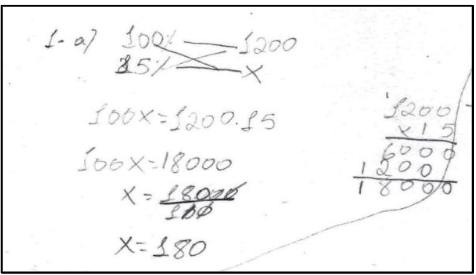
Nesse grupo, um estudante conseguiu resolver o problema mentalmente, mas apresentou muita dificuldade em sistematizar o modo de sua resolução. Após observar a discussão e o professor fazer alguns questionamentos, um outro aluno foi percebendo que se tratava da regra de três e a partir de então, conseguiram chegar ao resultado já conhecido pelo grupo por meio do colega. Embora o resultado final do valor não aparece nos cálculos apresentados, durante a socialização o estudante subtraiu o valor do desconto à vista do valor total, ou seja: (1200 – 180).
O grupo 02 utilizou o processo da divisão de fração e a multiplicação para obter o resultado solicitado (Figura 2).
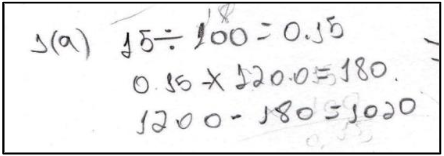
Percebe-se claramente que a equipe representou a porcentagem por meio dos números decimais e multiplicou pelo valor da bicicleta, encontrando o valor do desconto. A partir deste, subtraiu o valor encontrado do preço inicial da bicicleta e encontrou o valor pago na condição à vista. O grupo 03 usou o procedimento semelhante ao grupo 02, encontrando o mesmo resultado.
O grupo 04 não descreveu a forma que fez para achar o valor do desconto, mas escreveu a solução do problema (Figura 3).
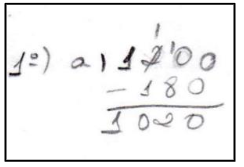
Já o grupo 05 não acertou a solução da questão. A Figura 4, abaixo, expõe o procedimento por eles utilizado.

É perceptível que o grupo fez a subtração de quinze por cento de cem por cento. O resultado multiplicou por um mil e duzentos. Do novo total, resolveu dividir por cem, segundo o grupo, referente ao setenta e cinco por cento. Para o grupo, o valor encontrado não foi o valor do desconto pois, sem dúvida, a bicicleta ficaria muito barata, então, subtraíram o valor inicial do valor encontrado (1200-900) para encontrarem o que eles definiram como o desconto dado à bicicleta.
No que se refere o item “b” da primeira questão, os grupos procederam de forma semelhante a resolução do item “a”. No entanto, o grupo 05 não respondeu à questão. O Grupo 01 utilizou a regra de três simples (Figura 5).
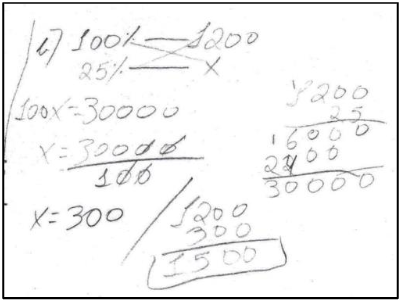
O grupo chegou ao valor que um cliente pagaria caso comprasse a mercadoria pagando a prazo, porém, não responda o que perguntava o problema, a diferença, em reais, entre as duas opções de compra, onde deveria efetuar a subtração do resultado encontrado no item “b” pelo do item “a”, ou seja, 1500 – 1020.
Para obter o resultado, o grupo 02 utilizou a divisão de fração e as operações: multiplicação, soma e subtração (Figura 6).

O grupo 03 não conseguiu expressar claramente como chegou ao resultado, acertando parcialmente a questão.

O grupo afirmou que 1200 adicionado a vinte e cinco por cento seria igual a 1500. No entanto, não explicou como encontrou o valor de 1500. Daí tentou subtrair 1500 de 1200, embora tenha expressado a escrita da operação invertendo as parcelas, o que daria um resultado negativo. Assim, procedeu a soma do valor da bicicleta com o valor encontrado da subtração e achou os 1500 que havia sido mencionado no início da solução do problema.
O grupo 04 procedeu de modo semelhante ao grupo 02, acertando a questão e o grupo 05 não respondeu.
A questão dois, nenhum grupo encontrou a solução, apenas o grupo 01 tentou a solução, porém está não estava correta. O grupo 02 tentou esboçar a resposta, mas não terminou a questão.
O Grupo 01 não interpretou corretamente o problema, pois entendeu que o prêmio a que o problema se refere seria dividido de forma igual entre os quatros jogadores, o que não era verdade.
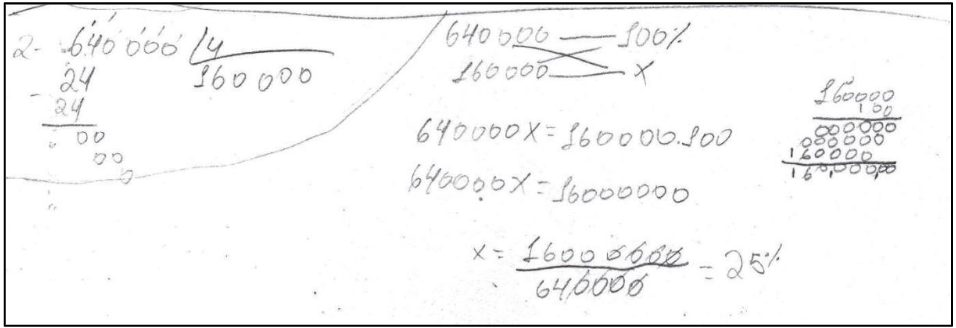
Conforme mostram os cálculos do grupo 01, cada jogador recebeu R$ 160.000,00, pois eles dividiram o valor total do prêmio pelos quatro jogadores e converteram o valor encontrado em porcentagem, utilizando a regra de três simples. Nesse sentido a solução apresentada pelo grupo foi incorreta.
Seguindo o mesmo raciocínio do grupo 01, o grupo 02 pretendia dividir o prêmio entre os quatros jogadores, no entanto, a equipe deparou-se com a dificuldade de operar a divisão do valor total do prêmio, conforme a Figura 9 abaixo ilustra.

A equipe 02 não expôs a resposta da questão 2 no quadro, apenas o grupo 01 que socializou a questão, por ser o único que respondeu todas as questões.
Após a socialização, passamos para a etapa plenária, onde discutimos as respostas expressas no quadro. Analisamos as estratégias usadas para resolução da questão 1 e todos puderam perceber como solucioná-la. Em seguida tratamos da questão dois e o debate foi mais longo. Identificamos que não conseguiram interpretar o fato de que o prêmio não seria dividido por igual e sim seria dividido de acordo o saldo de gol, ou seja, proporcionalmente. Superada a questão interpretativa, procedeu-se a resolução da questão.
Nesta etapa plenária, eles puderam perceber que as duas estratégias utilizadas para resolver a questão 2 eram relativamente fáceis, entretanto, concluíram que na metodologia de RP a interpretação do problema tem um papel fundamental. Houve relatos apontando para o fato de que a resolução em grupo, em determinado momento, atrapalhou, pois, uma opinião influenciava o pensamento do outro. Houve alguns que confidenciaram que nunca haviam vivenciado a metodologia da RP e que essa exige muita concentração. Como essas etapas realizadas demoraram além do previsto, o tempo de dois períodos de aula, a etapa seguinte, relativa à sistematização do conteúdo acabou ficando para a próxima aula.
Ao retornar à sala de aula para encerramento do projeto de intervenção, mais um encontro de duas horas de aulas foi destinado para a formalização do conteúdo e para a proposição de novas situações problemas. Nesta aula utilizamos uma apresentação de slides para discutirmos o conteúdo de Porcentagem. Cabe esclarecer que, apesar de inicialmente o projeto ter sido estruturado para se trabalhar com o tema da Porcentagem e de Juros, devido a etapa plenária ter tomado um tempo maior que o previsto, optamos por cancelar o trabalho com Juros.
Durante a exposição do conteúdo, os estudantes pouco questionaram, comportando-se como observado na aula com a professora titular. À medida que os exemplos iam sendo apresentados pelo professor regente, eles solicitaram que, antes da solução final ser apresentada, se poderiam tentar solucionar os exemplos em seus cadernos, o que prontamente foi atendido. Neste momento não foram seguidas todas as etapas propostas por Allevato e Onuchic (2011), mas observando as estratégias utilizadas, percebemos que a maioria respondeu de forma colaborativamente, auxiliando, opinando sobre o melhor meio para se resolver os exemplos propostos.
Após a sistematização do conteúdo, foi proposto a resolução de outras situações problemas. Com intuito de facilitarmos e otimizar o tempo, os problemas foram entregues em uma folha digitada. Sem que houvesse nenhum comando, grupos se formaram espontaneamente os quais seguiram algumas etapas realizadas na aula anterior. Tanto estratégias já utilizadas por cada grupo como as socializadas (incluindo a dos diferentes grupos e as expostas pelo professor) foram utilizadas na resolução dos novos problemas.
Depois de resolvidos e de alguns demonstrarem na lousa como chegaram à solução, o projeto de intervenção foi finalizado. Na avaliação final do professor regente a RP como metodologia de ensino mostrou-se efetiva e compatível com os objetivos do projeto de intervenção.
5. Considerações finais
Neste trabalho foi possível evidenciar algumas potencialidades que o ensino através da RP permite alcançar. Partindo do contexto escolar considerado e da questão de pesquisa estabelecida, foi possível verificar que a hipótese assumida encontrou respaldo nos dados obtidos e analisados na pesquisa. Em particular, foi possível identificar que o projeto de intervenção contribuiu para uma maior protagonismo dos estudantes, uma postura de equipe na busca de estratégias de resolução dos problemas propostos, uma mobilização de conhecimentos prévios ( como o conceito de porcentagem e os recursos matemáticos como a regras de três), além da percepção por parte dos estudantes da importância das habilidades de compreensão (na leitura dos enunciados dos problemas), argumentação (no âmbito do grupo ao defenderem seus pontos de vista) e reflexão (ao incorporarem novas estratégias disponibilizadas durante as etapas de socialização e formalização dos conteúdos). Cabe ainda mencionar que o uso da RP possibilitou liberdade para que os estudantes escolhessem o melhor meio de resolução dos problemas, sem se prenderem a uma fórmula/receita específica.
Os aspectos positivos foram evidentes, no entanto, alguns problemas em seu desenvolvimento foram identificados, talvez o mais importante foi o fato que os estudantes, ao iniciarem as atividades, manifestaram certa rejeição com relação à abordagem metodológica. Tal resistência, em princípio, caracterizou-se pelo fato de ao receberem o primeiro conjunto de problemas não conseguirem entendê-lo e nem mesmo identificarem a incógnita, já que esperavam uma sistematização do conteúdo preliminarmente à atividade de resolução de problemas.
Em outro momento, na etapa plenária, percebeu-se certo receio para apresentarem as soluções encontradas, uma vez que elas podiam estar erradas. Este temor justifica-se porque, tradicionalmente, há uma a supervalorização do acerto (obtenção da resposta certa) e uma punição ao erro. No caso da RP, entendemos que ela propicia um espaço avaliativo mais amplo e, assim, é possível, a partir do "erro", se produzir, através da reflexão, novos conhecimentos.
Cabe registrar que o uso da RP como metodologia de ensino exige do professor maior dedicação, avaliação contínua, além de um planejamento para a escolha adequada de situações-problema que permitam estimular a curiosidade e a motivação. Como já mencionado, essa metodologia faz com que eles utilizem seus conhecimentos matemáticos já adquiridos e desenvolvam a capacidade de interpretar e administrar as informações a que tem acesso (sejam as disponibilizadas no problema, sejam as que surgem na interação com os colegas e com o professor), estimulando-os a defender, justificar, argumentar e negociar com os colegas as suas próprias ideias. Assim, os estudantes ampliam seu conhecimento, desenvolvem seu raciocínio lógico e lidam com a matemática em seu contexto de aplicação.
Apesar das dificuldades apresentadas pelos estudantes, sobretudo durante as discussões, reforçamos que ficou evidente como o processo por eles mobilizado ao resolverem um problema constitui um elemento formativo importante. Ademais, ao descreverem como chegaram aos resultados, perceberam-se como atores ativos na construção de seus conhecimentos matemáticos, inclusive apontando para a importância da colaboração com os demais membros do grupo e o papel das diferentes ideias na resolução dos problemas.
Esperamos com esse trabalho ter podido contribuir para que a RP enquanto metodologia de ensino possa estimular outros docentes a conhecê-la e, eventualmente, adotá-la em seus contextos de ensino.
6. Referências
ALLEVATO, Norma Suely Gomes; ONUCHIC, Lourdes de La Rosa. Ensino-Aprendizagem-Avaliação de Matemática: Por que Através da Resolução de Problemas? In: ONUCHIC, Lourdes de La Rosa. et al. (Orgs.). Resolução de Problemas: Teoria e Prática. Jundiaí: Paco Editorial, 2014.
AMARAL, R.; SANT’ANA, I. P.; SANT’ANA, C C.. História do Ensino de Aritmética no Brasil: análise do manual “Metodologia do Ensino Primário”-1932. Com a Palavra, o Professor, v. 4, n. 8, p. 357-400, 26 abr. 2019. http://revista.geem.mat.br/index.php/CPP/article/view/347 Acesso em: 14 out. 2020.
BRASIL. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Matemática. Secretaria de Educação Fundamental. Brasília: MEC /SEF, 1998.
BRASIL. Ministério da Educação e Cultura. Base Nacional Comum Curricular – BNCC, versão aprovada pelo CNE, novembro de 2017. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf Acesso em: 19 mai. 2020.
DINIZ, M. I. Resolução de problemas e comunicação. In: SMOLE, K. S.; DINIZ, M. I. Ler, escrever e resolver problemas: habilidades básicas para aprender matemática. Porto Alegre: Artmed, 2001. p. 87-97.
GERHARDT, T. E.; SILVEIRA, D. T.. Métodos de pesquisa. Porto Alegre: Editora da UFRGS, 2009.
GONZÁLEZ, F. E.. “El Corazón de la Matemática” en la formación de futuros profesores de matemática. Revista de Educação Matemática, v. 17, p. e020011, 1 maio 2020. DOI 10.37001/remat25269062v17id245. Disponível em: https://www.revistasbemsp.com.br/REMat-SP/article/view/245. Acesso em: 4 jul. 2020.
LIMA, R. N.; GALVÃO, M. E. E. L.. Registro das etapas da Resolução de Problemas como recurso para um melhor desempenho de estudantes em vários níveis de escolaridade. Revista de Educação Matemática, v. 17, p. e020027, 1 maio 2020. DOI 10.37001/remat25269062v17id281. Disponível em: https://www.revistasbemsp.com.br/REMat-SP/article/view/281. Acesso em: 4 jul. 2020.
LIMA, R. F.. As pesquisas sobre resolução de problema no âmbito do EBRAPEM. Revista de Educação Matemática, v. 17, p. e020009, 1 maio 2020. DOI 10.37001/remat25269062v17id242. Disponível em: https://www.revistasbemsp.com.br/REMat-SP/article/view/242. Acesso em: 4 jul. 2020.
MAGNUS, M. C. M.. Professor e tecnologia: a postura do educador de matemática, no município de São João do Sul/SC, diante dos avanços tecnológicos. Trabalho monográfico (Especialização em Educação Matemática), da Universidade do Sul de Santa Catarina, 2010.
MENEGHELLI, J.; CARDOZO, D.; POSSAMAI, J. P.; SILVA, V. C.. Metodologia de resolução de problemas: concepções e estratégias de ensino. Revista Brasileira de Ensino de Ciências e Tecnologia, Ponta Grossa, v. 11, n. 3, p. 211-231, set./dez. 2018. Disponível em https://periodicos.utfpr.edu.br/rbect/article/view/6763 acesso em 03 mai. 2020.
MINAYO, M. C. S. (Org.). Pesquisa social: teoria, método e criatividade. Petrópolis: Vozes, 2011.
NUNES, C.; VIDAL, T.. Resolução e formulação de problemas no desenvolvimento do raciocínio combinatório. Com a Palavra, o Professor, v. 2, n. 4, p. 80-104, 2 out. 2017.
ONUCHIC, L. de La R.; ALLEVATO, N. S. G.; NOGUTI, F. C. H.; JUSTULIN, A. M. (Orgs). Resolução de problemas: teoria e prática. Jundiaí: Paco Editorial, 2014.
ONUCHIC, L. de La R. Uma História da Resolução de Problemas no Brasil e no Mundo. In: I Seminário em Resolução de Problemas – Palestra de Encerramento. São Paulo. 2008. Disponível em http://www.rc.unesp.br/serp/trabalhos_completos/completo3.pdf. Acesso em 10 Abr. 2020.
ONUCHIC, L. de La R. A Resolução e Problemas na Educação Matemática: onde estamos? E para onde iremos? Espaço Pedagógico, vol. 20, n° 1, Passo Fundo, p.88-104, jan/jun. 2013. Disponível em: http://seer.upf.br/index.php/rep/article/view/3509/2294 . Acesso em: 10 Abr. 2020.
ONUCHIC, L. De La R. Ensino-aprendizagem de matemática através da resolução de problemas. In: BICUDO, M. A. V. (Org.) Pesquisa em Educação Matemática: concepções e perspectivas. São Paulo: Editora UNESP, 1999. p. 199-218.
ONUCHIC, L. de La R.; ALLEVATO, N. S. G. Pesquisa em Resolução de Problemas: caminhos, avanços e novas perspectivas. Boletim de Educação Matemática, vol. 25, núm. 41, diciembre, 2011.
POSSAMAI, J. P.; SILVA, V. C.. Comunicação Matemática na Resolução de Problemas. Revista de Educação Matemática, v. 17, p. e020026–e020026, 1 maio 2020. DOI 10.37001/remat25269062v17id277. Disponível em: https://www.revistasbemsp.com.br/REMat-SP/article/view/277. Acesso em: 4 jul. 2020.
POLYA, G. A Arte de Resolver Problemas: um novo aspecto do método matemático. Tradução e adaptação, Heitor Lisboa de Araújo, 2 reimpressão. Rio de Janeiro: Editora Interciência, 1995.
POZO, J. I. A Solução de Problemas: aprender a resolver, resolver para aprender. Porto Alegre: Artmed, 1998.
SANTOS, Emily Vasconcelos; ANDRADE, Silvanio. Resolução, Exploração e Proposição de Problemas nos anos iniciais do ensino fundamental: contribuições para o ensino e aprendizagem da combinatória. Revista de Educação Matemática, v. 17, p. e020030, 1 maio 2020. DOI 10.37001/remat25269062v17id293. Disponível em: https://www.revistasbemsp.com.br/REMat-SP/article/view/293. Acesso em: 4 jul. 2020.
SEVERINO, Antônio Joaquim. Metodologia do trabalho científico. 2. ed. São Paulo: Cortez, 2017.
SCHOENFELD, A. H. Porquê toda essa agitação acerca da resolução de problemas? In: ABRANTES, P.; LEAL, L. C.; PONTE, J. P.. Investigar para aprender Matemática (textos selecionados). Lisboa: Associação dos Professores de Matemática, 1996. p. 61-71.
VAN DE WALLE, J. A. Matemática no ensino fundamental: formação de professores e aplicação em sala de aula. Tradução: Paulo Henrique Colonese. 6. ed. Porto Alegre: Artmed, 2009.
SENAI. Apostila Matemática Básica: Raciocínio lógico e análise de dados. Curso Assistente Administrativo, SENAI, 2015.
SILVEIRA, Adriano Alves da; ANDRADE, Silvanio de. Ensino-Aprendizagem de Análise Combinatória via Exploração, Resolução e Proposição de Problemas no Ensino Médio. Revista de Educação Matemática, v. 17, p. e020017–e020017, 1 maio 2020. DOI 10.37001/remat25269062v17id259. Disponível em: https://www.revistasbemsp.com.br/REMat-SP/article/view/259. Acesso em: 4 jul. 2020.
SANTOS, M. B. Q. C. P.; DYNNIKOV, C. M. S. S.; SANT’ANA, C. de C.; FERNANDES, E. P.; SANT’ANA, I. P. . A Resolução de Problemas Matemáticos nas Revistas de Ensino e Legislação: Alagoas, Bahia e Rio Grande do Sul, 1920-1960. In: PINTO, Neuza Bertoni; VALENTE, Wagner Rodrigues. (Org.). Saberes matemáticos em circulação no Brasil: dos documentos oficiais às revistas pedagógicas, 1890-1970. 1ed.São Paulo: Editora Livraria da Física, 2016, v. 1, p. 145-186.
Notas
Ligação alternative
https://www.revistasbemsp.com.br/index.php/REMat-SP/article/view/478 (pdf)

