Mathematical Modeling and teachers? formation: a discussion on mathematical knowledge for teaching

MODELAGEM MATEMÁTICA E FORMAÇÃO DE PROFESSORES: UMA DISCUSSÃO SOBRE O CONHECIMENTO MATEMÁTICO PARA O ENSINO

LA MODELIZACIÓN MATEMÁTICA Y LA FORMACIÓN DE PROFESORES: UNA DISCUSIÓN SOBRE EL CONOCIMIENTO MATEMÁTICO PARA LA ENSEÑANZA

Revista de Educação Matemática

Sociedade Brasileira de Educação Matemática, Brasil

ISSN: 1676-8868

ISSN-e: 2526-9062

Periodicity: Cuatrimestral

vol. 16, no. 21, 2019

sbem.sp.revista@gmail.com

Received: 15 August 2018

Accepted: 06 November 2018

Published: 01 January 2019

URL: http://portal.amelica.org/ameli/jatsRepo/173/1731528002/index.html

DOI: https://doi.org/10.25090/remat25269062v16n212019p5a17

This work is licensed under Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International.

In this article, we present a discussion that stemmed from a research project on Mathematical Modeling as a learning environment in teaching practice, which offered an investigation opportunity on the continuing professional development of Mathematics teachers in the early years of primary school. Such discussion is based on the Mathematical Modeling theme and on studies developed by Ball (2000), Ball, Hill and Bass (2005), Hill, Rowan and Ball (2005), Ball, Thames and Phelps (2008) and Ball, Hill and Shilling (2008), which focused on discussions about mathematical knowledge for teaching.

The aim of this study is to understand if and how the continuing professional development of teachers through Mathematical Modeling can contribute to mathematical knowledge for teaching. Through this perspective, Ball (2000) stresses the importance of addressing three problems in order to contribute to students? learning:

the first problem concerns identifying the content knowledge that matters for teaching, the second regards understanding how such knowledge needs to be held, and the third centers on what it takes to learn to use such knowledge in practice (BALL, 2000, p. 01).

We understand that each of these actions, as supported by Ball (2005), involves knowledge of mathematical ideas, of mathematical thinking skills and of their communication, as well as the competence to use examples, analogies and relations necessary for the comprehension of these ideas.

During our research, we learned that the use of Mathematical Modeling as a learning environment can be presented as a highly favorable scenario to foment necessary discussions to investigate the knowledge harnessed by teachers all along their continuing professional development process. Thus, we could discuss mathematical knowledge for teaching and help teachers so that they understand that it is necessary to think about the problems mentioned by Ball (2000), which must be taken into consideration in order to have better learning results.

Therefore, we start to introduce our understanding of Mathematical Modeling, of teachers? continuing professional development and a discussion on the theory presented by Ball and her collaborators. Next, we present our final considerations, where we discuss a possible approach between the use of Modeling for teachers? continuing professional development and the ideas discussed by Ball and her collaborators about Mathematical Knowledge for Teaching.

Previous studies on Mathematical Modeling and its possibility of application both in the continuing professional development of teachers and in the classroom show a considerable growth in the number of research studies on this theme that have been conducted in recent years, for instance the ones by Barbosa (2001, 2010), Luna (2012), Caldeira (2013), Barbosa, Caldeira and Araújo (2007), Oliveira and Barbosa (2010, 2011), Almeida and Dias (2007), among others. They have discussed the possibilities, tensions and strategies about the use of Modeling ¹in the classroom, for teachers? formation and, especially, for their continuing professional development.

The growing number of research studies involving Modeling and teachers? formation, and the publication of their results ?have boosted the improvement of training courses and enabled innovative experiences? (BISOGNIN, E; BISOGNIN, V. 2012, p.1). In this sense, Modeling has been presented as a strategy that has contributed substantially to the process of teaching and learning Mathematics.

Some of these studies (for example, BARBOSA, 2002; OLIVEIRA, 2007 and ALMEIDA AND DIAS, 2007) stress the need for reflection about the process of formation of a teacher as an essential element of the educational process, corroborating the concept defended by Escudero (1992). She stated that every curriculum change, as well as its implementation, must be pondered as a group-decision process involving the agents who will develop the ideas in practice. In accordance with this notion, it is difficult to advocate for a perspective of change that does not stimulate learning and at the same time seeks to promote relearning in individuals and in their practice in order to promote changes that contribute to their development and, consequently, to the development of society. According to Almeida and Dias (2007, p. 265), for example, ?teachers? contacts with Modeling offer subsidies to the development of new understandings about Mathematics and its teaching, which may have impact on their classroom practice?.

In our point of view, to encourage this reflection and teachers? involvement, it is necessary to rethink the patterns through which teachers? formation happens when it comes to the offer of practices that contribute to make their engagement more participatory, critical and reflexive throughout the teaching and learning process. Therefore, we agree with Barbosa (2001) about teachers? formation. The author wrote that

[...] a teacher?s professional development does not merely involve criticality, but it is constituted by it, by questioning and inquiring. The whole purpose consists of building conditions so that one reflects on teachers? and trainers? experiences (BARBOSA, 2001, p. 55).

The importance of rethinking teachers? training and, especially, their continuing professional development is at the core of the discussion that we propose in this article, once we agree with the idea that teachers? professional practice consists of making decisions in a process through which they give shape to themselves and acquire their professional identity ². Here we have the same understanding about decision-making as discussed by Giesta (2001, p. 55), who tells us that

Decision-making is essentially defined as teachers? behavior before their teaching actions, considering the perception that they have of their conceptions, their thoughts, their social-political-professional role and their knowledge developed all along their professional development process and/or in the educational practice that they implement?.

This decision-making process also reflects social, political and economic transformations, as well as educational changes, which have demanded new reflections about the formation and the professional identity of teachers, who should now be considered social players equipped with such autonomy that enables them to identify their personal theoretical choices, their knowledge gaps, their level of compromise towards their students, schools and communities, their technical competence, their omissions, inter alia.

Studies on the use of Modeling in the continuing professional development of teachers have shown that it has been a favorable way to encourage teachers to rethink their knowledge, conceptions and beliefs concerning Mathematics and its teaching.

In our research study, we especially propose a discussion that involves Modeling in the continuing development of Mathematics teachers in the early years of primary school, in which we apply Modeling to inspire actions as a way of fomenting the discussion on teaching because it involves, among other elements, the beliefs and conceptions that teachers have about Mathematics and its teaching.

Barbosa (2001, p. 5)highlights that ?since conceptions are formed in the aggregation of experiences, one must use them to unbalance conceptions that are deeply entrenched.? Such statement supports our understanding that the continuing development of teachers must encourage their experiences and lead them to reflection, that is, without losing sight of teachers? practical or professional knowledge because we are in unison with the idea that innovative experiences interfere with teachers? conceptions.

According to what Caldeira (2009) says, the continuing development of teachers must break ties with conceptions based on technical rationality in a way that formation is not seen as a finished event. On the contrary, based on training and capacity-building, we need to acknowledge that teachers? formation processes happen in a sequence of actions and evaluations that involve teaching and learning.

Therefore, we reiterate that the continuing development of teachers must stimulate new learning and promote relearning in individuals and in their teaching practices, so that they are able to promote changes that contribute to their professional development. Consequently, teachers will develop a more participatory, critical and reflexive attitude throughout the teaching and learning process and will also propose actions to challenge their beliefs about Mathematics and teaching.

These arguments support our belief that teachers? contacts with Modeling offer subsidies to the development of new understandings about Mathematics and teaching. We believe that Modeling - through Barbosa?s (2001, 2002) perspective, which is supported by us in this study - can be developed in the continuing development of teachers as a basis for a dialogical, collective and critical construction of knowledge. It is also important to take into consideration Caldeira?s (2009) words

We are all cultural products made up of beliefs, values, rules, objects, meanings, knowledge and everything that can be characterized as inherent to human beings, who are historically determined by our time?s conditions and by the environment in which we live (CALDEIRA, 2009, p. 37).

Beliefs and conceptions about Mathematics and teaching are not the only elements that shape a teacher?s attitude; pedagogical knowledge is also important. This is discussed by Chaves and Espírito Santo (2011) in their studies on the continuing development of teachers. These authors stressed the importance of Doerr?s (2007) studies when they argued that teachers must have deep pedagogical knowledge as well as the need for knowledge of conceptual nature that involves mathematical knowledge, its teaching and learning, especially when it comes to working with Modeling activities. They think that it is difficult for teachers to perform these activities or even to establish useful relations for their students without considerable mathematical knowledge or knowledge of learning processes.

Chaves and Espírito Santo (2011) also state that when teachers perform modeling activities, they build knowledge that will produce changes in their practices, in a way that they can see Mathematics and its teaching through a different perspective. This is also described by D?Ambrósio (1993), who encouraged searching for an alternative to shift focus from merely teaching mathematical content to a methodology that helps students develop skills to be able to apply Mathematics to real life situations. By doing so, they will create theories that may be appropriate for various situations and enable the identification of the most suitable information for each situation, as well as the specific conditions to identify suitable contents and methodologies for any level. These actions can also contribute towards finding new ways in which the teacher can interact with knowledge and with students in the classroom, so that they can help strengthen a

non-characterization of a kind of Mathematics education in which students merely learn what they will need to use next week, in their daily lives, but a kind of education that selects and presents the necessary mathematical content for a comprehension of their reality and the strengthening of social ties (CALDEIRA, 2009, p. 37).

The discussion that we have promoted up to this point enables us to highlight the importance of using Mathematical Modeling in the continuing development of teachers because it can encourage them to build new knowledge to foster changes in their practice through actions that may result in new ways of dealing with knowledge and with students in the classroom.

Due to our concern about how teachers handle knowledge and how they behave towards the way their students learn, we analyzed previous studies in search of authors that investigated these relations and their consequences. As a result, we found the work developed by Ball and her collaborators, whose discussions have revolved around the mathematical knowledge that a teacher needs for teaching.

Thus, we believe that using Mathematical Modeling as a learning environment provides a highly favorable scenario to produce necessary discussions in order to investigate the knowledge harnessed by teachers throughout their continuing development, so we are able to discuss mathematical knowledge for teaching. For that reason, we will start to show our understanding of this theory that approaches the necessary knowledge for a professional to teach Mathematics.

In recent years, studies published by Ball (2000), Ball, Hill and Bass (2005), Hill, Rowan and Ball (2005), Ball, Thames and Phelps (2008) and Ball, Hill and Shilling (2008) have investigated and discussed what necessary knowledge a teacher must have so that he can teach Mathematics. Starting with the systematization of their studies, they presented a model for Mathematical Knowledge for Teaching.

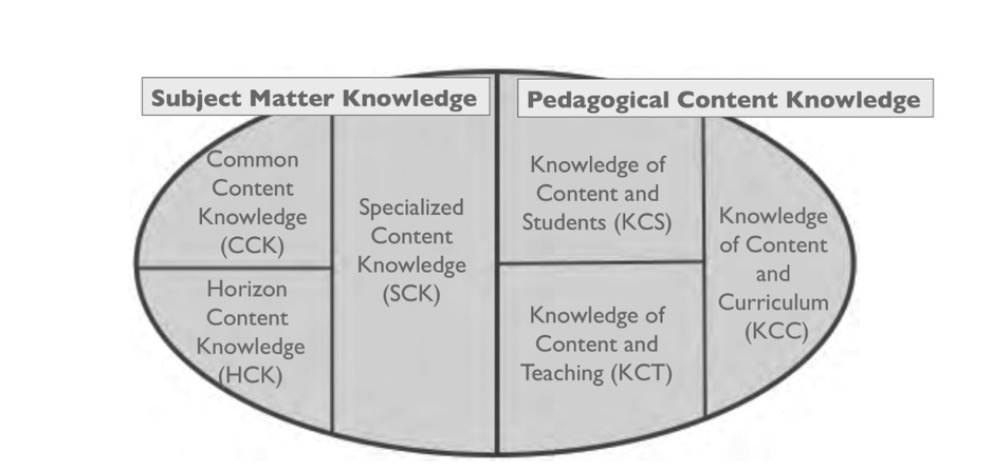
Figure 1
Domains of Mathematical Knowledge for Teaching
Source: Ball, Thames e Phelps (2008, p. 403).

Domains of Mathematical Knowledge for Teaching

Source: Ball, Thames e Phelps (2008, p. 403).

The figure shows the correspondence between the map of domains of mathematical knowledge for teaching, as proposed by the authors, and two of the categories introduced in Schulman?s (1986) early works: subject matter knowledge and pedagogical content knowledge. In this map created by the authors, the third category presented by Schulman (ibid.), called Knowledge of Curriculum, appears as a subdomain of Pedagogical Content Knowledge.

Nevertheless, the authors highlight that the table is not presented in a definitive form because they are not entirely sure that this subdomain can be a part of the Knowledge of Content and Teaching subdomain, or if it can be connected to several other subdomains. Furthermore, the writers temporarily included a third subdomain inside the category Knowledge of Content and Teaching, which they named Horizon Content Knowledge. For a better understanding and description of the subdomains presented in the model, we point out the following characteristics:

(a) the left side of the figure is called Subject Matter Knowledge and it is divided into the following subdomains: (i) Common Content Knowledge which, in general terms, can be described as knowledge used to perform the work of a teacher just like it is used in other professions and occupations that also make use of Mathematics; (ii) Specialized Content Knowledge, which refers to mathematical knowledge and to unique teaching skills, enabling teachers to dedicate to activities that are teaching-specific; (iii) Besides these two subdomains, the authors introduce the concept of Horizon Content Knowledge. This is presented as knowledge related to the awareness of where some specific mathematical content is located in the extension of the Mathematics range included in the curriculum, that is, the need to know how the Mathematics that they teach in a given year is related to the Mathematics that students will learn in subsequent years;

(b) the right side of the figure contains the elements related to Pedagogical Content Knowledge and it is divided into the following subdomains: (a) Knowledge of Content and Students, which is content that combines knowledge of students and Mathematics; (b) Knowledge of Content and Teaching, which combines knowledge of teaching and Mathematics. Besides these two subdomains, the authors introduce the concept of Knowledge of Content and Curriculum.

When they refer to Mathematical Knowledge for Teaching, the authors stress that when teachers search for patterns in their students? mistakes, or when they analyze that a non-standard approach would work, in general they need to perform a kind of mathematical work that other professionals do not perform; a kind of work that involves an extraordinary type of mathematical discovery that is not necessary in situations out of teaching/learning environments. Therefore, it reaffirms the writers? conception that performing teaching tasks demands unique mathematical understanding and thinking ? a kind of knowledge that is beyond the knowledge being taught to students.

One of our concerns is to comprehend what mathematical knowledge is harnessed by the teachers who are participating in the continuing development, that is, to understand what mathematical knowledge they are using in the classroom to produce the appropriate instruction and to make their students learn.

We highlight that our interest in investigating teachers? knowledge is not restricted to knowledge of the content that they teach, but of the special forms of mathematical knowledge that are required so that one can teach Mathematics, because they must also hold additional forms of useful knowledge to do their work in the classroom.

During our research on mathematical knowledge for teaching, we are interested in learning how familiarized teachers are with the aspects of their students? mathematical thinking and what strategies they learn to identify common mistakes made by their students which, as discussed by Ball, is an element of knowledge for teaching. An important observation made by the author is that a teacher must also try to identify if and how such knowledge, as we identify it, is related to the improvement of students? learning in Mathematics.

In line with the studies conducted by these authors, our aim is to understand what teachers do in their Mathematics teaching practice and how they do it. Instead of worrying about how curricular requirements influence what they teach, or about the standards which they are responsible for, we focus on understanding their work. Based on studies by these authors, we understand that ?teaching ^4? means all actions that teachers harness to contribute to their students? formation.

We assume that teachers need competence in mathematical terms and in speech that allow a careful mathematical work towards students? learning; a work that will not produce mistakes or misconceptions. Students, for their part, need definitions that are useful to them, based on terms and ideas that they have previously understood, which demands that teachers have knowledge beyond the definitions, concepts and rules that they may generally find in their initial formation.

In this article, one of our concerns is to search for evidence to analyze ifand howModeling can be used in order for teachers to reveal and improve their mathematical knowledge for teaching. Moreover, we aim at learning if and how Modeling can provide teachers with situations in which they need to demonstrate their common knowledge, their specialized content knowledge and knowledge of content and teaching so that they reveal what they know about conceptions and misconceptions that their students may have about a specific subject, for instance. In this sense and in agreement with the work developed by Ball and her team, this type of research work prioritizes specific forms of discussion, according to which teaching requires a simultaneous integration between the ideas that are fundamental to the content and the methodology through which students learn the content.

The circumstances presented by us show that there is a clear need for opportunities that allow teachers not to merely know Mathematics, but to learn how to effectively use what they know in a range of contexts during their teaching practice. These ideas lead us to agree with Ball?s (2000) conception that we need to approach the following problems: (i) understand what teachers must know, (ii) how they must know it and (iii) develop ways to help them learn how to use it. By solving these three problems, we could help fill the gaps that usually prevent progress in a teacher?s professional development. After all, these are the conditions that support the issue concerning teachers? content preparation in their classroom practice.

To conduct our research, we chose to work with Modeling in continuing development of teachers in a way that prioritizes practice. This characteristic can also be found in works by Ball and her collaborators, for this proposal contributes to discussing and understanding what aspects of a given content teachers need to know in addition to what they will teach. Besides, it will help encourage discussions on how and where they can use this mathematical knowledge in their practice.

According to Ball (2000), it?s necessary to provide teachers with opportunities to learn some mathematical content not only to know it for themselves, but to be able to learn how to use it in a range of practical contexts. Thus, the author emphasizes that understanding what teachers need to know - and how they need to know it ? and helping them learn how to use that knowledge could help them fill the gaps that usually prevent progress in teachers? formation, since these are the issues concerning teachers? content preparation in their practice,

Modeling in teacher formation allowed us to identify not only what teachers knew about the mathematical content that was being approached. It also enabled us to understand how they see and deal with the problems that are related to the content, and to understand what they are able to harness mathematically when they are teaching their students. As a consequence of it, and in order to improve our comprehension of what level of content knowledge should be important to teachers so that they can teach it, we aimed at discussing and identifying some activities that are fundamental to the teaching process.

Stemming from this comprehension, Ball and her collaborators argue about the need to concentrate our efforts to discuss the nature of this additional knowledge, by wondering, for example, what teachers must know in practice about Mathematics to achieve success in the classroom with their students. Such comprehension, according to the authors, supports the discussion on the model of Mathematical Knowledge for Teaching presented by them.

This conception stresses the necessity of refuting the paradigm that emphasizes that teachers who have knowledge of the content they need to teach are able to use such knowledge for teaching. Here we can identify the problem related to how the content must be understood so that it can be harnessed for teaching. In this sense, we understand that merely increasing teachers? opportunities for studying Mathematics is insufficient to enhance their teaching skills.

The utilization of Modeling proved to be a favorable environment to create opportunities for teachers to learn the content not only to have it for themselves, but especially to learn how to use what they know in a range of everyday contexts. Research work by Ball and her collaborators emphasizes that the simple act of teaching a given content may not solve the problem regarding its practical use, because teachers need elements to understand the activities that are essential to their work.

In this sense, we observed that the application of Modeling in teacher formation contributes to break ties with a technical rationality that is also characterized by the presentation of exercises about a given content right after such content has been explained by the teacher. In a scenario like this, it is not commonplace to decide which content must be used to solve a problem, but to make use of a set of concepts and properties from the latest content studied.

Modeling favored the improvement of Specialized Content Knowledge because teachers learned new arguments, new ways of finding and representing solutions by trying to use mathematical language in a proper manner. The discussions stimulated during the development of learning situations contributed to the necessary knowledge for early years primary school Mathematics teachers to teach and to give new meanings to their work, taking into consideration the change of conception regarding necessary knowledge for teaching.

So, in addition to offering fundamental knowledge to teaching, the formation process contributed to teacher formation by initiating discussions which translated into elements used to help build teachers? autonomy, which in turn strengthened their will to overcome the challenges they face in their daily teaching practice and encouraged them to pursue their professional development.

Building an environment in which problem solving goes beyond identifying and applying correct calculation procedures is a considerable challenge. For this reason, it is necessary to make use of Modeling in continuing development of teachers in order to change their practice in a significant way.

http://www.revistasbemsp.com.br/index.php/REMat-SP/article/view/225 (pdf)