Artigos Científicos
O ensino de Transformações Geométricas: uma análise dos cadernos do aluno e do professor do Estado de São Paulo
THE TEACHING OF GEOMETRIC TRANSFORMATIONS: AN ANALYSIS OF THE STUDENTS 'AND TEACHERS' NOTEBOOKS IN THE STATE OF SÃO PAULO
LA ENSEÑANZA DE TRANSFORMACIONES GEOMÉTRICAS: UN ANÁLISIS DE LOS CUADERNOS DEL ALUMNO Y DEL PROFESOR DEL ESTADO DE SÃO PAULO
Recepção: 27 Julho 2018
Aprovação: 21 Setembro 2018
Publicado: 01 Maio 2019
URL: http://portal.amelica.org/ameli/jatsRepo/173/1731527003/index.html
DOI: https://doi.org/10.25090/remat25269062v16n222019p210a231

Este trabalho está sob uma Licença Creative Commons Atribuição-NãoComercial-Não Derivada 4.0 Internacional.
A atuação do professor em sala de aula pode ser conduzida a partir de duas vertentes: por um lado, pelo seu conhecimento teórico e pela sua experiência, construída por meio da sua prática em sala de aula; por outro, por meio de documentos elaborados por entidades de esferas federais, regionais, estaduais e municipais, que irão orientar os conteúdos a serem abordados em cada uma das etapas do ensino. Este artigo é direcionado para a segunda vertente, e assim, apresenta a seguinte questão diretriz: Como é apresentado o conteúdo matemático de transformações geométricas nos materiais curriculares do Estado de São Paulo? A partir desta questão, temos como objetivo analisar e discutir a abordagem utilizada para o ensino das transformações geométricas nos Cadernos do Aluno e Cadernos do Professor do Estado de São Paulo.
Para esclarecer esta questão e cumprir este objetivo, será apresentado um breve histórico da motivação da concepção dos Cadernos do Aluno e do Professor do Estado de São Paulo 1, e do Currículo Oficial do Estado de São Paulo, bem como para que tais documentos foram desenvolvidos, e explicitado seu papel no ensino e na aprendizagem. Ainda, será discutida a relação que os professores possuem com estes materiais, e apresentadas as propostas de tais documentos para o ensino do conteúdo matemático de transformações geométricas.
Posteriormente, serão descritos os critérios elaborados para a análise das situações de aprendizagem 2envolvendo transformações geométricas presentes nesses documentos e a discussão dessas situações a partir dos critérios previamente estabelecidos. Com base nesta análise, será abordada a forma como a apresentação desse conteúdo nesses documentos aos professores e aos estudantes reflete no seu ensino e na sua aprendizagem.
Na revisão de literatura foi observado um número crescente de trabalhos que tratam destes materiais, tanto na área da Matemática como em outras áreas, já que eles são utilizados por toda a rede de ensino do Estado de São Paulo. Porém, ainda existem aspectos a serem explorados e analisados nos cadernos, em especial sobre o tópico de transformações geométricas. Assim, fica ainda mais evidente a importância dos resultados desta pesquisa, bem como a sua difusão para o embasamento de trabalhos futuros.
A seguir, apresentaremos uma síntese da importância do ensino de transformações geométricas e das suas abordagens metodológicas, com enfoque para os tipos de tarefas pelas quais essas transformações podem ser abordadas e para os Documentos Oficiais do Estado de São Paulo, segundo a revisão de literatura sobre essa temática.
Segundo Wagner (2007), as transformações geométricas são um tópico da Matemática, mais especificamente da Geometria, em que, a partir de uma construção geométrica primária, são realizadas outras, que conservam certas propriedades em relação à construção original. Elas podem ser reflexões em relação a um ponto ou a uma reta, rotações e translações, que são transformações isométricas, em que medidas como distâncias entre pontos, ângulos, perímetros e áreas são conservadas; ou ampliações e reduções, denominadas homotetias, em que se obtém uma construção geométrica semelhante a original, conservando apenas as medidas dos ângulos desta.
De acordo com os Parâmetros Curriculares Nacionais (PCN),
os conceitos geométricos constituem parte importante do currículo de Matemática no ensino fundamental, porque, por meio deles, o estudante desenvolve um tipo especial de pensamento que lhe permite compreender, descrever e representar, de forma organizada, o mundo em que vive. A Geometria é um campo fértil para se trabalhar com situações-problema e é um tema pelo qual os estudantes costumam se interessar naturalmente. O trabalho com noções geométricas contribui para a aprendizagem de números e medidas, pois estimula a criança a observar, perceber semelhanças e diferenças, identificar regularidades e vice-versa. ( BRASIL, 1998, p. 39)
Tratando especificamente do ensino de transformações geométricas, Marschall e Fioreze (2015) descrevem que elas facilitam a abordagem de conceitos como números e medidas, semelhanças e diferenças, e de regularidades ou não entre diversas estruturas, sem que haja a necessidade de realizar previamente uma definição formal. Portanto, contribuem para potencializar habilidades visuais do estudante, desenvolvendo nele uma organização do pensamento matemático necessária para a compreensão de demais conteúdos, inclusive de outras disciplinas.
O ensino de transformações geométricas pode ser realizado por diversas formas, sendo uma delas a utilização de tarefas. Segundo Ponte (2014, p. 21, grifos do autor), essas são ferramentas utilizadas para auxiliar na mobilização de conceitos e processos matemáticos, e diversas tarefas destinadas a uma determinada situação correspondem a uma atividade. Assim, as tarefas podem ser classificadas em quatro perspectivas: ?um exercício é uma tarefa fechada e de desafio reduzido; um problema é uma tarefa também fechada, mas com desafio elevado; uma investigação é uma tarefa aberta com desafio elevado; uma exploração é uma tarefa aberta e acessível à maioria dos alunos?.
A partir de tais noções teóricas, apresentaremos uma breve descrição dos Documentos Oficiais do Estado de São Paulo, cuja finalidade é definir parâmetros mínimos e fornecer materiais básicos para o ensino de Matemática para a sua rede pública de ensino.
A elaboração e a implementação do Currículo Oficial do Estado de São Paulo se deram por meio do Programa São Paulo Faz Escola, implantado pela Secretaria de Estado da Educação de São Paulo, em 2008, e adotado como currículo oficial em 2010. Sua elaboração, bem como a dos Cadernos, justifica-se com base nos resultados observados nas provas do Sistema de Avaliação de Rendimento Escolar do Estado de São Paulo (SARESP), e tem como objetivo elevar o desempenho dos estudantes nesse sistema de avaliação do ensino ( CASSIARI, 2011; CATANZARO, 2012). Portanto, todos os documentos elaborados neste programa têm como enfoque principal as referidas provas.
Segundo descrito no próprio Currículo, sua função é o de apresentar uma base comum de conhecimentos e competências mínimas para o desenvolvimento escolar do estudante, e também deste como cidadão ( SÃO PAULO, 2012). O Currículo Oficial é acompanhado de um Caderno do Gestor, que tem como finalidade ?apoiar o gestor para que ele seja um líder capaz de estimular e orientar a implementação do Currículo nas escolas públicas estaduais de São Paulo? ( SÃO PAULO, 2012, p. 7-8), e dos Cadernos do Aluno e do Professor ( SÃO PAULO, 2014a, 2014b), apresentados na seção 1.3 do documento.
O texto afirma que o Currículo Oficial se faz necessário para fornecer uma educação pública de qualidade e possibilidades de desenvolvimento pessoal acessíveis a todos. Para tal, é essencial que a escola compreenda o contexto de seus estudantes, e ?aprenda a ensinar? ( SÃO PAULO, 2012). Assim, este documento é apresentado de maneira mais ampla, buscando não especificar os conteúdos, mas introduzindo-os a partir de competências e habilidades.
Especificamente tratando do conteúdo de Matemática, o Currículo do Estado de São Paulo: Matemática e suas tecnologias divide o conteúdo a ser ensinado nos anos finais do Ensino Fundamental e no Ensino Médio em três grandes blocos: Números, Geometria e Relações. Para abordá-los, propõe que sejam utilizados os Cadernos do Aluno e do Professor, em conjunto com o livro didático, e argumenta que tais materiais fornecem elementos suficientes para que os blocos propostos sejam trabalhados em sua completude, de maneira inter e intradisciplinar. Ademais, fornece subsídios para que o professor utilize recursos didáticos e metodologias de ensino diversificadas ( SÃO PAULO, 2012). A apresentação do conteúdo é dividida por anos escolares e, dentro deles, por bimestres, em que um dos três blocos geralmente predomina; e é feita por meio de quadros, que descrevem o conteúdo a ser abordado e as habilidades a serem desenvolvidas a partir dele.
Na sequência, serão apresentadas as características mais relevantes para esta pesquisa nos Cadernos do Aluno e do Professor.
Os Cadernos do Aluno e do Professor, assim como o Currículo, são materiais de apoio elaborados como produtos do Programa São Paulo Faz Escola, destinados a estudantes e professores dos Anos Finais do Ensino Fundamental e Ensino Médio. ?O Caderno do Professor auxilia os mais de 240 mil docentes do ensino de São Paulo no preparo das aulas e no desenvolvimento das atividades?, enquanto o Caderno do Aluno ?auxilia na qualidade do ensino, pois propicia o mesmo nível de aprendizado para todos os alunos da rede estadual paulista? ( SÃO PAULO, 2008, p. 1).
Com base no que foi apresentado, podemos inferir que os resultados a serem obtidos por meio do uso desses materiais estão diretamente ligados com a relação dos professores e dos estudantes com esses Cadernos. Este aspecto será brevemente discutido a seguir.
Com base nos dados descritos anteriormente, entendemos que os Cadernos do Aluno e do Professor podem ser utilizados apenas como complementos do livro didático e de outros recursos utilizados pelo professor. Fiamengui (2009) aponta que a implementação do Programa São Paulo Faz Escola, e, consequentemente, dos Cadernos do Aluno e do Professor, não passou por consulta aos professores, e tampouco teve sua elaboração compartilhada com eles, o que foi responsável por despertar nesses profissionais uma resistência à sua implementação. Ainda, Fiamengui (2009) descreve que os conteúdos propostos pelos Cadernos não eram condizentes com o que estava sendo trabalhado pelos professores no momento de sua implementação, e que esses não receberam a formação adequada para usufruir desse material, o que pode ser evidenciado pela transcrição da fala de um dos professores, apresentada a seguir:
Não houve preparação para ninguém, ninguém estava receptivo naquele momento, foi constrangedor, posso dizer isso quando a gente não prepara uma aula para nossos alunos com antecedência, tudo vira um caos. Precisa ser feito um trabalho anterior, motivador, mostrar quais são os objetivos, trabalhar com argumentações. Imposições jamais. ( FIAMENGUI, 2009, p. 101).
Assim, podemos conjecturar que não houve uma preocupação para que os profissionais utilizassem toda a potencialidade fornecida pelos materiais curriculares que estavam sendo oferecidos pelo referido Programa, o que fez com que a implementação do projeto e dos materiais propostos não atingissem a eficácia e os objetivos previstos nele.
A seguir, serão apresentados os procedimentos metodológicos utilizados neste artigo, bem como os critérios utilizados para elaborá-los.
Os Cadernos do Aluno e do Professor utilizados para a elaboração deste artigo são da versão 2014-2017, apresentados em dois volumes por ano escolar, cada um deles destinado a um semestre. Os Cadernos possuem o mesmo conteúdo, quando considerado o mesmo ano/volume, porém com apresentações diferentes, que serão descritas posteriormente.
Neste artigo, serão apresentadas as situações de aprendizagem (discutidas na seção 7) que tratam das transformações geométricas, dos dois volumes dos Cadernos do Aluno e do Professor referentes à disciplina de Matemática, dos Anos Finais do Ensino Fundamental e Ensino Médio, em que duas delas, uma do Ensino Fundamental e outra do Ensino Médio, serão discutidas e analisadas com maior profundidade.
Para a realização desta pesquisa, utilizamos como base os critérios de análise apresentados por Stylianides (2007), que realiza uma reflexão de como os materiais curriculares podem auxiliar o professor a desenvolver, nos estudantes, habilidades de demonstrações e/ou provas. Adaptando tais critérios para o contexto desta pesquisa, as situações de aprendizagem para o ensino do conteúdo matemático de transformações geométricas presentes nos Cadernos do Professor foram analisadas qualitativamente a partir dos seguintes aspectos:
1- Identificar se as situações propostas fornecem aos professores subsídios suficientes para oportunizar a exploração das transformações geométricas por parte dos estudantes.
2- Verificar se as situações propostas oferecem apenas soluções únicas ou se são fornecidas ao professor outras formas de conduzir a atividade, que possibilitem outras soluções.
Em Stylianides (2007) foram analisados os materiais curriculares direcionados somente ao professor. Aqui, estenderemos esta análise também aos materiais curriculares destinados aos estudantes. Logo, nas situações de aprendizagem propostas nos Cadernos do Aluno, foram observados qualitativamente os seguintes aspectos:
1- As situações de aprendizagem propostas podem ser definidas como exercícios, problemas, investigações e/ou explorações que visam contribuir para aprendizagem dos estudantes?
2- As situações de aprendizagem expressam relação do conteúdo estudado com outros conteúdos matemáticos e com o cotidiano dos estudantes?
Sendo assim, as situações de aprendizagem propostas nos Cadernos do Aluno e do Professor passaram por uma primeira análise, mais geral, com um olhar direcionado para os aspectos descritos anteriormente. A partir desta primeira observação, foram selecionadas duas situações de aprendizagem: uma delas referente ao Ensino Fundamental e a outra, relativa ao Ensino Médio, para que passassem por uma análise mais aprofundada e fossem discutidas neste artigo.
Antes, serão apresentados os conteúdos matemáticos de transformações geométricas presentes nos Documentos Oficiais do Estado de São Paulo.
Neste tópico, apresentaremos os dados da pesquisa. Primeiramente, a caracterização dos Cadernos do Aluno e do Professor e a distribuição do conteúdo de transformações geométricas no Currículo do Estado de São Paulo e nos Cadernos do Aluno e do Professor.
Os Cadernos do Aluno possuem seu conteúdo dividido em situações de aprendizagem, de acordo com os tópicos a seguir. Eles podem estar ou não todos presentes nas situações de aprendizagem, bem como em outras sequências, ou então apresentados mais de uma vez em uma mesma situação de aprendizagem:
- Contextualização da Atividade: breve apresentação da atividade a ser realizada, a partir de exemplos. Como se trata de um material de apoio, não apresenta de forma sistemática as definições teóricas ou conceitos, necessitando que o professor realize as intervenções teóricas necessárias na apresentação dos conteúdos.
- Leitura e Análise de Texto: em alguns momentos, a situação de aprendizagem é apresentada por uma leitura de texto, na maioria das vezes, relacionada com a história da Matemática. Tal leitura por vezes aparece em outros momentos de algumas situações de aprendizagem, a fim de complementar o conteúdo apresentado.
- Você Aprendeu?: exercícios e/ou atividades de verificação do conteúdo, que devem ser feitos em sala de aula, com o auxílio do professor, e podem aparecer introduzindo a situação de aprendizagem.
- Lição de Casa: exercícios semelhantes à seção ?Você Aprendeu?, que devem ser realizados em casa pelo estudante, desta vez, sem o auxílio do professor.
- Pesquisa Individual: propostas de projeto de pesquisa a ser realizado fora do ambiente escolar do estudante, relacionado com o conteúdo que está sendo estudado.
- O Que eu Aprendi: espaço para que o estudante anote suas considerações.
- Desafio: problemas mais complexos que os apresentados anteriormente, que podem ser de exames e/ou vestibulares, relacionados com o conteúdo abordado.
Os Cadernos do Professor possuem uma seção introdutória com uma orientação geral sobre eles, propondo ao professor a flexibilidade de aprofundar mais ou não aqueles conteúdos que desejar, uma breve síntese do que é esperado do estudante nesta etapa de aprendizagem, e o que se espera que o professor trabalhe nas situações de aprendizagem, cada uma subdividida em unidades específicas sobre os conteúdos a serem abordados.
Na descrição detalhada de cada situação de aprendizagem, é exposto, primeiramente, um quadro indicativo de conteúdos e temas, competências e habilidades, e sugestão de estratégias, relacionados com tal situação de aprendizagem. Em seguida, é apresentado um roteiro para o procedimento docente na aplicação de cada uma das atividades propostas; os aspectos a observar nas ações dos estudantes enquanto executam as tarefas propostas; e as soluções esperadas. Por fim, são propostas sugestões de como o professor deve proceder na avaliação dos estudantes, de acordo com o perfil da atividade realizada.
Os dois primeiros quadros a seguir mostram a distribuição/organização de conteúdos referentes às transformações geométricas em cada um dos anos/bimestres do Ensino Fundamental e Médio do Currículo do Estado de São Paulo: Matemática e suas tecnologias; a especificação desses conteúdos; os blocos (Números, Geometria, Relações) a que pertencem; e as habilidades a serem desenvolvidas por eles:
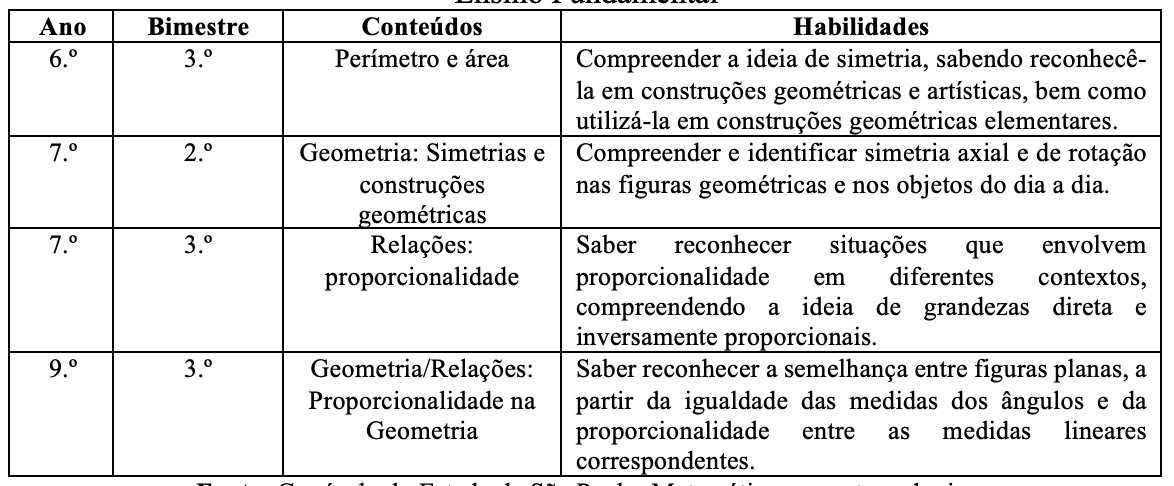
Quadro 1
Conteúdos e habilidades de Matemática que envolvem transformações geométricas no Ensino Fundamental
Currículo do Estado de São Paulo: Matemática e suas tecnologias

Quadro 2
Conteúdos e habilidades de Matemática que envolvam transformações geométricas no Ensino Médio
Currículo do Estado de São Paulo: Matemática e suas tecnologias
Os próximos quadros expõem a distribuição/organização de conteúdos referentes às transformações geométricas em cada um dos anos/volumes dos Cadernos do Aluno e do Professor no Ensino Fundamental e Médio; a especificação desses conteúdos; e as situações de aprendizagem em que eles aparecem:
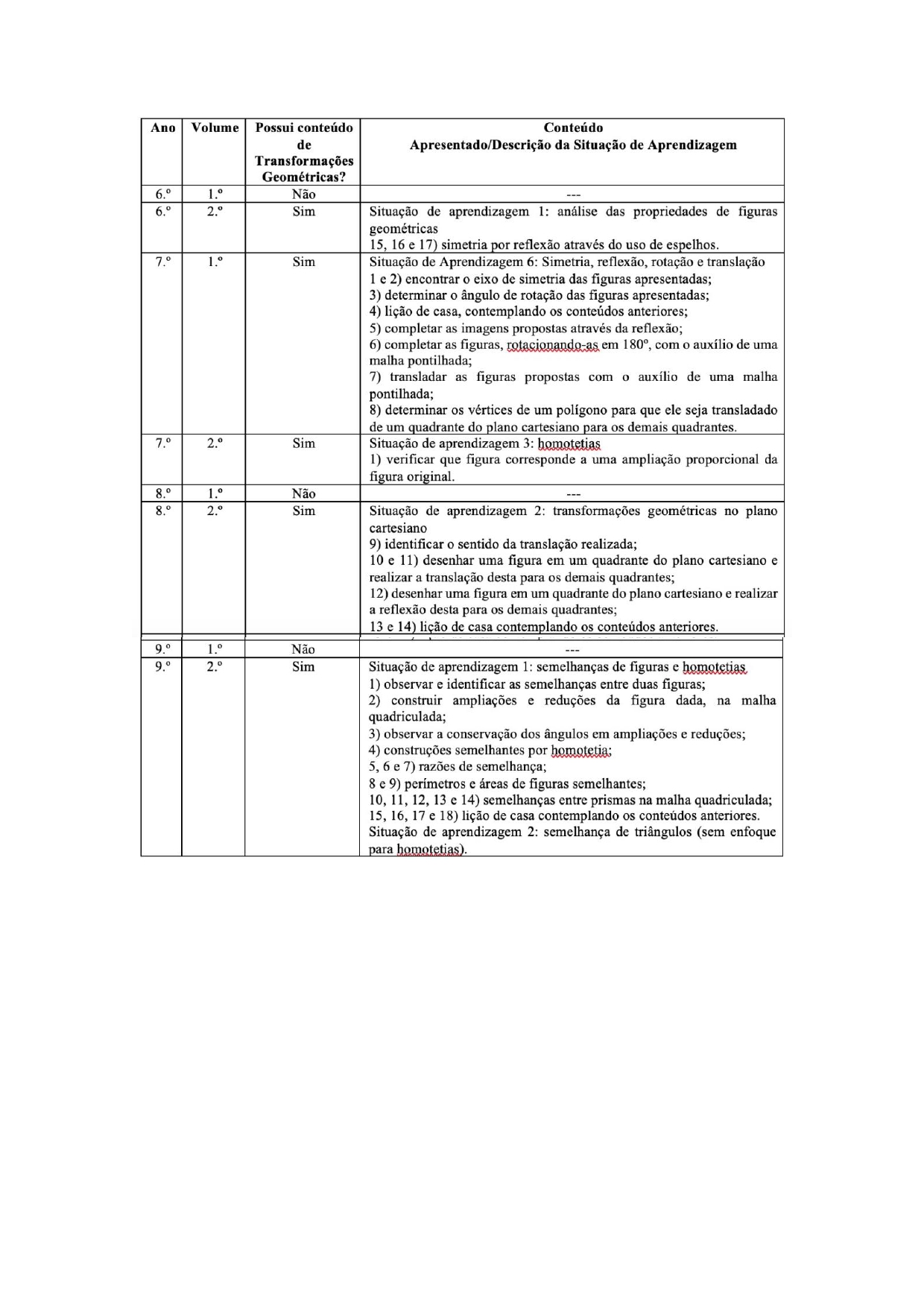
Quadro 3
Cadernos do Professor e do Aluno no Ensino Fundamental
Autores

Quadro 4
Cadernos do Professor e do Aluno no Ensino Médio
Autores
Comparando os Quadros 1 e 3, que tratam dos conteúdos de transformações geométricas designados ao Ensino Fundamental, respectivamente, no Currículo Oficial e nos Cadernos do Aluno e do Professor, há uma correspondência entre o que tais materiais apresentam, o que condiz com a proposta do Programa São Paulo Faz Escola, visto que os Cadernos são um material de apoio ao conteúdo proposto pelo Currículo. A única discrepância é observada na situação de aprendizagem 2 do 2.º volume, destinado ao 8.º ano do Ensino Fundamental, uma vez que os conteúdos de transformações geométricas são abordados significativamente por meio do plano cartesiano, e em contrapartida, no Currículo, neste estágio, é descrito somente o trabalho com o plano cartesiano, desprezando o fato de que as transformações geométricas também são trabalhadas nesta situação de aprendizagem.
Quanto ao Ensino Médio, foram comparados os Quadros 2e 4, que tratam, respectivamente, dos conteúdos propostos para esta etapa do ensino no Currículo e nos Cadernos do Aluno e do Professor. Também não se observaram grandes discrepâncias, ainda mais considerando que no Ensino Médio os principais conceitos de transformações geométricas já foram definidos, e nesta etapa do ensino serão apenas aplicados. Logo, o Currículo mostra apenas os momentos em que essa aplicação ocorre de forma mais significativa, enquanto nos Cadernos do Aluno e do Professor foram identificados alguns outros momentos em que as transformações geométricas aparecem, porém com menor relevância.
O tópico seguinte apresentará duas situações de aprendizagem selecionadas ? uma referente ao Ensino Fundamental e outra referente ao Ensino Médio ? e a discussão delas com base nos aspectos definidos nos procedimentos metodológicos, analisando os Cadernos do Professor e do Aluno.
A situação de aprendizagem selecionada ( Figura 1) é intitulada: ?Refletindo e Girando com Simetria?. Ela foi escolhida por ser a primeira em que são definidos os conceitos e as propriedades principais das transformações geométricas 3.

Figura 1
?Refletindo e Girando com Simetria?
Caderno do Aluno, volume 1, 7.º ano do Ensino Fundamental
Considerando que esta definição inicial de conceitos será responsável pela construção de conceitos posteriores e que, se não for realizada corretamente, pode implicar em possíveis dificuldades em etapas futuras de aprendizagem, consideramos importante discuti-la.
No Caderno do Professor, como já foi descrito anteriormente, é apresentado um quadro contendo os conteúdos e os temas, as competências e as habilidades, e sugestões de estratégias para ensino do conteúdo proposto. Assim, temos:

Figura 2
Quadro Síntese da Situação de Aprendizagem: ?Refletindo e Girando com Simetria?
Caderno do Professor, volume 1, 7.º ano do Ensino Fundamental.
A seguir, é apresentado um roteiro de como o professor deve proceder na execução da situação de aprendizagem. Segundo este roteiro, o professor deve discutir com os estudantes as definições e as aplicações da palavra ?simetria?; apresentar e discutir os conceitos de simetria axial (ou de reflexão) e simetria de rotação; identificar a quais transformações geométricas elas correspondem e como realizar tais transformações.
Posteriormente, são apresentadas as mesmas tarefas presentes no Caderno do Aluno, porém, já com a solução desejada indicada. A primeira tarefa propõe que sejam traçados os eixos de simetria de figuras distintas, e a tarefa seguinte sugere que o aluno identifique o ângulo de rotação das figuras apresentadas, apenas observando quantas simetrias rotacionais a figura possui. Da mesma forma, procede-se com as demais tarefas, sempre com uma descrição do que o estudante deve efetuar em cada uma delas. Assim, são propostas cinco tarefas com esta mesma estrutura.
Em seguida apresenta-se para o professor o recurso das malhas quadriculadas ou malhas de pontos e propõe-se a ele que as utilize para explorar os conceitos desejados por esta situação de aprendizagem. São ainda propostas tarefas que utilizam esses recursos, como completar parte das figuras já iniciadas nas malhas para que contemplem o conceito desejado (simetria axial ou rotacional).
Após o trabalho com os conceitos de simetria, reflexão e rotação, sugere-se que o professor introduza aos estudantes o conceito de translação, dando exemplos, como os movimentos da Terra, que ele possa utilizar para aplicá-los com os estudantes. Depois oferecem tarefas que tratam desses conceitos, solicitando ao estudante que realize a translação da figura apresentada na malha pontilhada na direção e no sentido indicados.
Por fim, o material sugere que o professor inicie o trabalho de transformações geométricas num plano coordenado, com o objetivo de que o estudante se familiarize com ele, indicando que este conceito será trabalhado mais detalhadamente no futuro. Assim, apenas uma atividade envolve translações e plano cartesiano, onde os estudantes devem determinar as coordenadas de um polígono para que ele seja transladado simetricamente para os demais quadrantes do plano.
Finalizando esta situação de aprendizagem, são propostas considerações sobre como o professor deve avaliar a aprendizagem dos estudantes dos tópicos trabalhados, enfatizando que os objetivos são que os estudantes apenas tenham um primeiro contato com as transformações geométricas, e que elas serão aprofundadas posteriormente. Também sugere ao professor que ele forneça a maior diversidade de situações possível, para que ele identifique os conceitos desejados e amplie seu repertório. É proposto ao professor que ele realize a avaliação por meio de tarefas semelhantes às apresentadas nos Cadernos com o uso de malhas quadriculadas e pontilhadas, além de pedir para que o estudante recorte imagens com simetrias e identifique-as.
Com base nesta descrição, podemos observar que a situação de aprendizagem é estruturada de forma bastante diretiva, indicando sempre o que o professor deve fazer, inclusive na forma como ele deve avaliar os estudantes, possuindo apenas pequenas indicações de exploração pelo professor fora do conteúdo apresentado, e ainda assim, bastante direcionadas. Apesar de esta estrutura tentar garantir e padronizar uma aprendizagem mínima, ela pode ser perigosa, pois o professor pode se limitar a essas indicações e não buscar outros materiais que o auxiliem no ensino das transformações geométricas, que pudessem favorecer a aprendizagem dos estudantes.
Retomando os aspectos propostos nos procedimentos metodológicos, temos:
1- Identificar se as situações propostas fornecem aos professores subsídios suficientes para oportunizar a exploração das transformações geométricas por parte dos estudantes: o conteúdo presente nesta situação de aprendizagem, embora explicitado que se trata de uma introdução sobre transformações geométricas, poderia apresentar-se de forma mais aprofundada. Logo, cabe ao professor fornecer aos estudantes materiais de apoio, como livros didáticos, capazes de evidenciar uma definição formal, adequada ao nível dos estudantes, dos conceitos de simetria, reflexão, rotação e translação. Além disso, o professor pode usar recursos que ampliem a visualização da ocorrência da transformação geométrica desejada, o que pode ser feito por meio de uso de materiais manipulativos e/ou softwares de geometria dinâmica.
2- Verificar se as situações propostas oferecem apenas soluções únicas ou se são fornecidas ao professor outras formas de conduzir a atividade, que possibilitem outras soluções: as tarefas presentes nesta situação de aprendizagem apresentam uma única solução, e em raros casos é dada certa flexibilidade ao professor para trabalhar o conteúdo proposto de uma maneira diferente da apresentada pelos Cadernos. Para diversificar seu trabalho, o professor precisará recorrer a materiais como livros didáticos e paradidáticos, entre outros.
O Caderno do Aluno apresenta a situação de aprendizagem de forma muito semelhante ao Caderno do Professor, porém sem as indicações direcionadas a este ? apenas com as tarefas. Inicia-se já na primeira tarefa, de simetria, descrita no item anterior. Não apresenta nenhuma definição teórica, é apenas um material de tarefas, cabendo ao professor fazer tal abordagem. Como a descrição geral das atividades já foi realizada, passaremos para a discussão dos aspectos a serem observados:
1- As situações de aprendizagem propostas podem ser definidas como exercícios, problemas, investigações e/ou explorações que visam contribuir para aprendizagem dos estudantes? Como foi descrito anteriormente, neste momento, os conceitos de simetria, reflexão, rotação e translação são introduzidos para serem aprofundados posteriormente. Assim, todas as tarefas propostas são fechadas e de desafio reduzido, isto é, a abordagem é na forma de exercícios. Porém, mesmo como introdução de conteúdos, as tarefas poderiam ter um maior caráter exploratório ou um nível de dificuldade mais elevado. Portanto, compete ao professor propor, se considerar viável, tarefas de exploração e de investigação aos estudantes.
2- As situações de aprendizagem expressam relação do conteúdo estudado com outros conteúdos matemáticos e com o cotidiano dos estudantes? As situações de aprendizagem estão relacionadas a outros conteúdos matemáticos que serão trabalhados posteriormente (por exemplo, o plano cartesiano). No entanto, o cotidiano dos estudantes está apenas implícito nas situações de aprendizagem, pois seria muito difícil compor essas relações em um material destinado a todo o estado de São Paulo, em que cada cidade, cada bairro e/ou cada escola, possui um contexto social diferente. Logo, a situação de aprendizagem dá margem para tais relações, mas estas precisam ser realizadas pelo professor, de acordo com o contexto social em que sua escola e seus estudantes estão inseridos.
De acordo com os dados apresentados no Quadro 4, os conteúdos de transformações geométricas no Ensino Médio não são abordados diretamente, mas sim aplicados a outros conteúdos. Em contrapartida à situação de aprendizagem analisada anteriormente, selecionamos para análise e discussão a última situação de aprendizagem presente nos Cadernos em que essas transformações aparecem, além de que ser nesta situação de aprendizagem que elas são tratadas mais significativamente no Ensino Médio. A situação de aprendizagem selecionada ( Figuras 3 e 4) é intitulada: ?Números Complexos: Representação no Plano e Significado das Operações (Translações, Rotações, Ampliações)?.

Figura 3
?Números Complexos: Representação no Plano e Significado das Operações (Translações, Rotações, Ampliações)?
Caderno do Aluno, volume 1, 3.º ano do Ensino Médio.
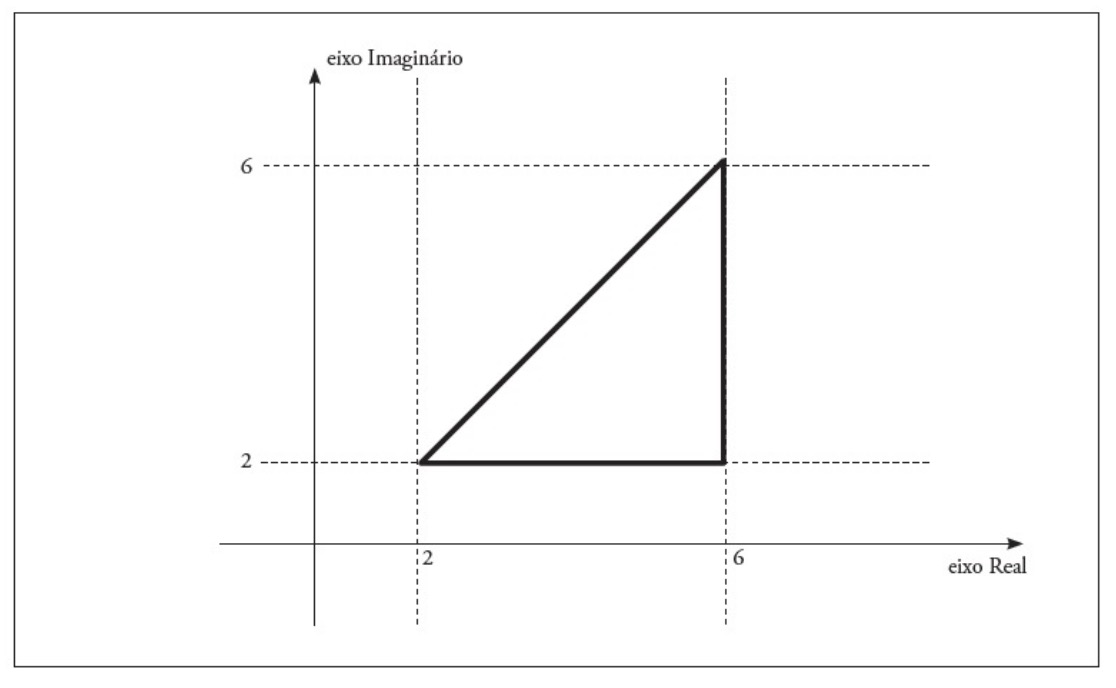
Figura 4
Tarefa envolvendo Transformações Geométricas na Situação de Aprendizagem: ?Números Complexos: Representação no Plano e Significado das Operações (Translações, Rotações, Ampliações)?
Caderno do Aluno, volume 1, 3.º ano do Ensino Médio.
No Caderno do Professor são definidos para esta situação de aprendizagem:

Figura 5
Quadro Síntese da Situação de Aprendizagem: ?Números Complexos: Representação no Plano e Significado das Operações (Translações, Rotações, Ampliações)?
Caderno do Professor, volume 1, 3.º ano do Ensino Médio.
O roteiro para aplicação da situação de aprendizagem inicia-se tratando da abordagem de ensino que o professor deve utilizar para ensinar o conceito dos números complexos. Como este conteúdo não faz parte do escopo desta pesquisa, esta etapa não será discutida aqui. Da mesma forma que na situação de aprendizagem discutida anteriormente, são apresentadas algumas discussões que o professor deve levantar sobre o conteúdo, seguidas das mesmas atividades presentes no Caderno do Aluno, porém, com as resoluções desejadas.
As transformações geométricas são abordadas nas tarefas 11 a 13, em que o estudante deve realizar a operação indicada na figura representada no plano cartesiano e verificar qual das transformações geométricas ocorre (translação ? vertical, horizontal ou ambas ?, rotação, ampliação ou redução). Esta é a única referência às transformações geométricas presente nesta situação de aprendizagem, e na seção de avaliação menciona-se que o professor deve realizar outras atividades que demonstrem a aplicação prática delas, pois as limitações 4do Caderno não permitem que sejam feitas nesse momento. Assim, quanto aos aspectos definidos nos procedimentos metodológicos para a análise e a discussão das situações de aprendizagem, temos:
1- Identificar se as situações propostas fornecem aos professores subsídios suficientes para oportunizar a exploração das transformações geométricas por parte dos estudantes: não há subsídios para a exploração das transformações geométricas de outras maneiras, além daquelas utilizadas em situações de aprendizagem anteriores, restando somente a indicação de que tal aprofundamento não cabe aos Cadernos nesse momento, e sim ao professor.
2- Verificar se as situações propostas oferecem apenas soluções únicas ou se são fornecidas ao professor outras formas de conduzir a atividade, que possibilitem outras soluções: tampouco as tarefas propostas nesta situação de aprendizagem referentes às transformações geométricas possibilitam que o professor as explore de outra maneira nesse nível de ensino, a não ser que ele recorra a outros materiais, ao invés do Caderno do Professor.
No Caderno do Aluno, a presença das transformações geométricas nesta situação de aprendizagem se dá exclusivamente pela utilização dos conceitos a elas referentes já estudados anteriormente, aplicados aos números complexos, sem maiores aprofundamentos ou propostas de outras utilizações delas. Sendo assim, sobre os aspectos de análise propostos, podemos destacar que:
1- As situações de aprendizagem propostas podem ser definidas como exercícios, problemas, investigações e/ou explorações que visam contribuir para aprendizagem dos estudantes? Novamente, as tarefas apresentadas são fechadas e de desafio reduzido, o que as caracteriza como exercícios. Ao contrário da situação de aprendizagem do Ensino Fundamental, que introduzem conceitos, aqui, por se tratar de um momento em que os estudantes já possuem um repertório conceitual mais amplo, esperar-se-ia que as tarefas propusessem uma demanda cognitiva mais aprofundada por parte dos estudantes. Mais uma vez, cabe ao professor propor tais tarefas, de cunho exploratório e de desafios.
2- As situações de aprendizagem expressam relação do conteúdo estudado com outros conteúdos matemáticos e com o cotidiano dos estudantes? Nesta situação de aprendizagem, vê-se a aplicação do conteúdo de transformações geométricas a outros conteúdos matemáticos, mostrando, portanto, que eles se relacionam. Porém não há a tentativa de fazer relação com o cotidiano, ficando ainda explícito que tal relação deve ser realizada pelo professor.
Dada a importância dos Cadernos do Professor e do Aluno para os processos de ensinar e de aprender Matemática nas escolas públicas do estado de São Paulo, buscamos neste artigo responder a questão Como é apresentado o conteúdo matemático de transformações geométricas nos materiais curriculares do Estado de São Paulo?, com o objetivo de analisar e discutir a abordagem utilizada para o ensino das transformações geométricas nos Cadernos do Aluno e Cadernos do Professor do Estado de São Paulo. Para tanto, nos baseamos em um olhar geral para a distribuição do conteúdo de transformações geométricas nos Anos Finais do Ensino Fundamental e no Ensino Médio, e, principalmente, na análise de duas situações de aprendizagem dos Cadernos do Professor e do Aluno.
Em particular, a análise do Caderno do Professor se baseou em dois tópicos. No primeiro: (1) identificar se as situações propostas fornecem aos professores subsídios suficientes para oportunizar a exploração das transformações geométricas por parte dos estudantes, identificamos que os subsídios de ensino não são suficientes para explorar o conteúdo de transformações geométricas, o que demanda que o professor busque outros materiais didáticos; e, no segundo tópico, (2) verificar se as situações propostas oferecem apenas soluções únicas ou se são fornecidas ao professor outras formas de conduzir a atividade, que possibilitem outras soluções, as situações propostas não apresentam diferentes formas de resolução e tampouco são fornecidas outras possibilidades de visualização das transformações geométricas, como a integração da geometria dinâmica, a qual potencializaria o estudo desse conteúdo.
A análise do Caderno do Aluno também envolveu dois tópicos. No primeiro: (1) as situações de aprendizagem propostas podem ser definidas como exercícios, problemas, investigações e/ou explorações que visam contribuir para aprendizagem dos estudantes?, detectamos uma carência de tarefas investigativas e a presença daquelas voltadas à resolução de exercícios, as quais também consideramos importantes no processo de aprendizagem, mas não suficientes para o estudo do conteúdo de transformações geométricas. No segundo tópico: (2) as situações de aprendizagem expressam relação do conteúdo estudado com outros conteúdos matemáticos e com o cotidiano dos estudantes?, há relações com outros conteúdos e a conexão com o cotidiano dos estudantes não está explícita nos Cadernos. Compete, portanto, ao professor realizá-la.
A partir dos resultados obtidos nas análises, pontuamos algumas perspectivas futuras de investigação. No que se refere aos Cadernos, sobre o conteúdo de transformações geométricas, temos: (a) ausência de instrução em como utilizá-lo; (b) revisão de tópicos que podem ser aprofundados, apesar de ter um conteúdo mínimo a ser ensinado, evitando a superficialidade de abordagem do conteúdo nos diferentes níveis de escolaridade, principalmente, no Ensino Médio; (c) ausência de definições matemáticas e necessidade de busca por outros materiais didáticos ou paradidáticos para o ensino, o que, possivelmente, ocorre na apresentação de outros conteúdos matemáticos dos Cadernos; e (d) oportunidades de formação continuada aos professores, em cursos e/ou grupos coletivos de formação, que discutam as transformações geométricas, com diferentes abordagens de ensino, ampliando as possibilidades de significação conceitual na preparação de aulas pelos professores, e, por conseguinte, potencializando a aprendizagem matemática dos estudantes.
http://www.revistasbemsp.com.br/index.php/REMat-SP/article/view/208 (pdf)

Quadro 1
Conteúdos e habilidades de Matemática que envolvem transformações geométricas no Ensino Fundamental
Currículo do Estado de São Paulo: Matemática e suas tecnologias

Quadro 2
Conteúdos e habilidades de Matemática que envolvam transformações geométricas no Ensino Médio
Currículo do Estado de São Paulo: Matemática e suas tecnologias

Quadro 3
Cadernos do Professor e do Aluno no Ensino Fundamental
Autores

Quadro 4
Cadernos do Professor e do Aluno no Ensino Médio
Autores

Figura 1
?Refletindo e Girando com Simetria?
Caderno do Aluno, volume 1, 7.º ano do Ensino Fundamental

Figura 2
Quadro Síntese da Situação de Aprendizagem: ?Refletindo e Girando com Simetria?
Caderno do Professor, volume 1, 7.º ano do Ensino Fundamental.

Figura 3
?Números Complexos: Representação no Plano e Significado das Operações (Translações, Rotações, Ampliações)?
Caderno do Aluno, volume 1, 3.º ano do Ensino Médio.

Figura 4
Tarefa envolvendo Transformações Geométricas na Situação de Aprendizagem: ?Números Complexos: Representação no Plano e Significado das Operações (Translações, Rotações, Ampliações)?
Caderno do Aluno, volume 1, 3.º ano do Ensino Médio.

Figura 5
Quadro Síntese da Situação de Aprendizagem: ?Números Complexos: Representação no Plano e Significado das Operações (Translações, Rotações, Ampliações)?
Caderno do Professor, volume 1, 3.º ano do Ensino Médio.


