1. Introdução

O ensino e a aprendizagem dos números racionais são sempre tarefas desafiadoras para docentes e discentes do ensino fundamental. As especificidades e várias distinções dos racionais em relação aos números naturais criam dificuldades para a compreensão dos alunos e requerem dos professores a mobilização de estratégias que facilitem uma apreensão significativa desse objeto matemático.

Com relação a tais dificuldades, a cerca de vinte anos atrás, os Parâmetros Curriculares Nacionais de Matemática ( BRASIL, 1998), em suas orientações didáticas, já apontavam algumas especificidades dos racionais não conhecidas pelos alunos nos anos iniciais da escolaridade, quando seu universo de representação numérica restringia-se ao conjunto dos números naturais, e que tornam esse objeto de difícil compreensão para alguns. Dentre elas, destacamos:

- Se o ?tamanho? da escrita numérica, no caso dos naturais, é um bom indicador da ordem de grandeza (8345 > 83), a comparação entre 2,3 e 2,125 já não obedece o mesmo critério;

- A comparação entre racionais: acostumados com a relação 3 > 2, terão de compreender uma desigualdade que lhes parece contraditória, ou seja, 1/3 < 1/2 ;

- Cada número racional pode ser representado por diferentes (e infinitas) escritas fracionárias: por exemplo, 1/3, 2/6, 3/9, 4/12,... são diferentes representações de um mesmo número (p. 101).

Com relação a esta série de peculiaridades próprias dos números racionais, Fernandes et al. (2008, p. 4) defendem que se trata de ?uma característica que merece atenção por parte dos educadores matemáticos e precisa ser considerada no contexto do ensino- aprendizagem como geradora de rupturas e continuidades, e também como fonte de dificuldades conceituais?.

Por sua vez, a Teoria dos Registros de Representação Semiótica - TRRS, desenvolvida pelo pesquisador Raymond Duval, defende a importância de se levar em consideração as várias representações de um mesmo objeto ao tratarmos sobre o processo de ensino-aprendizagem em matemática. Desse modo, a utilização dos seus variados tipos de registros e a coordenação entre eles aparece, portanto, como algo fundamental para uma eficaz apreensão do objeto matemático estudado ( DUVAL, 2003). Essa coordenação entre diferentes representações de um mesmo objeto matemático ocorre por tratamento, quando temos uma transformação acontecendo num mesmo tipo de registro, ou por conversão, quando na transformação ocorre a transição de um tipo de registro para outro ( DUVAL, 2003).

Para Duval (2003), muitas das dificuldades apresentadas pelos alunos estão relacionadas, principalmente, à sua capacidade de articular diferentes registros de representação e, embora esta atividade de conversão sempre exija um maior esforço cognitivo por parte do aluno, é, exatamente, neste exercício de promover transições entre um registro semiótico e outro que o aluno adquire novos conhecimentos e consegue reconhecer aspectos conceituais e propriedades do objeto matemático estudado, que se tornam mais evidentes em um ou outro registro.

Temos, portanto, no campo do ensino-aprendizagem em matemática um desafio relativo à abordagem dos números racionais, sobretudo no que tange à conversão entre os seus registros de representação, cuja suplantação passa pela identificação dos entraves que envolvem a compreensão deste objeto matemático e a elaboração de situações didáticas que auxiliem os alunos na superação de suas dificuldades.

Nesse sentido, os estudos em Educação Matemática frequentemente recomendam a utilização de materiais manipuláveis durante as aulas, pois, conforme Gitirana e Carvalho (2010, p. 38)tais recursos ?foram concebidos para serem manipulados pelos alunos. Só assim eles propiciam o início da construção dos conceitos e procedimentos básicos da matemática?.

Estes materiais didáticos manipuláveis concretos, como define Lorenzato (2006, p. 21), têm sua contribuição destacada como ?um excelente catalizador para o aluno construir o seu saber matemático?. Por sua vez, Turrioni (2004, p. 78) afirma que os materiais manipuláveis podem ser muito significativos ?para auxiliar ao aluno na construção de seus conhecimentos?.

Nesse artigo, trazemos um recorte da pesquisa intitulada ?Conversões entre Representações de Números Racionais: limites e possibilidades no uso de material manipulável?, desenvolvida no mestrado do Programa de Pós-Graduação em Educação Matemática e Tecnológica ? EDUMATEC-UFPE, com o objetivo de investigar, à luz da Teoria dos Registros de Representação Semiótica, limites e possibilidades no uso de material manipulável em conversões entre representações de números racionais (MELO, 2019).

2. Revisão de Literatura

A partir da aproximação com a literatura podemos observar que, conforme Mandarino (2010, p. 107), já desde os primeiros anos do ensino fundamental, ?os números racionais, em suas representações fracionárias ou decimais, já são objeto de estudo e causam muita preocupação aos professores e alunos?.

Há, no mínimo, três aspectos relacionados à aprendizagem dos números racionais que podemos citar como importantes na decisão de empreendermos estudos sobre este objeto matemático:

- Os vários significados que estes números podem assumir.

- As suas variadas representações simbólicas.

- As dificuldades observadas envolvendo o ensino e a aprendizagem deste objeto matemático.

Na literatura podemos encontrar nos trabalhos de autores como Kieren (1998), Behret al. (1983) e Ohlsson (1989) uma variedade de significados atribuídos ao número racional. Entre estes, os sentidos de número, medida, quociente, operador multiplicativo, taxa, razão, coordenadas lineares, parte-todo e interpretação parâmetro/parâmetro.

Assim como diferentes significados, os números racionais também admitem variadas representações que podem envolver expressões da linguagem natural falada ou escrita, formas figurativas e registros numéricos.

A linguagem natural é, para Duval (2011, p. 83), ?o primeiro registro de representação semiótica para o funcionamento do pensamento?. Podemos entender as representações em linguagem natural como expressões da linguagem natural falada ou escrita que, em nosso contexto, referem-se à utilização da linguagem matemática relativa a um conhecimento sistematizado que é interpretado e expresso de forma verbal ou textual.

As representações chamadas figurativas podem ser de quantidades contínuas ou discretas. As quantidades contínuas são aquelas as quais podemos dividir o seu todo em um número infinito de partes iguais sem que haja qualquer prejuízo de suas propriedades, como, por exemplo, a área de uma figura plana. Por sua vez, ao falarmos de quantidades discretas, estamos nos referindo àquelas cujo total não podemos dividir infinitamente, sob pena de prejuízo a suas propriedades, como, por exemplo, uma turma de alunos.

Quanto aos registros simbólico-numéricos, os números racionais podem ser representados em formas percentuais, decimais e fracionárias.

O significado mais aplicado aos registros fracionários, desde os primeiros anos escolares, é o de parte de um todo. Nesse caso, a representação a/b relaciona, respectivamente, número de partes consideradas / números de partes ?iguais? que foi dividido o todo ou inteiro.

Nunes et al. (2003), salienta que a ideia por trás dessa concepção é a de partição de um todo contínuo em . partes iguais, bastando, portanto, o emprego da técnica de dupla contagem para resolver a maior parte dos exercícios dessa natureza, ou seja, acima do ?traço? coloca-se o número de partes consideradas e abaixo o número total de partes.

Na figura 1, apresentamos exemplos de algumas possíveis representações para o número racional ?um quarto?:

Figura 1: Esquema de representações para o racional ?um quarto?

Figura 1
Esquema de representações para o racional um quarto
(Melo, 2019)

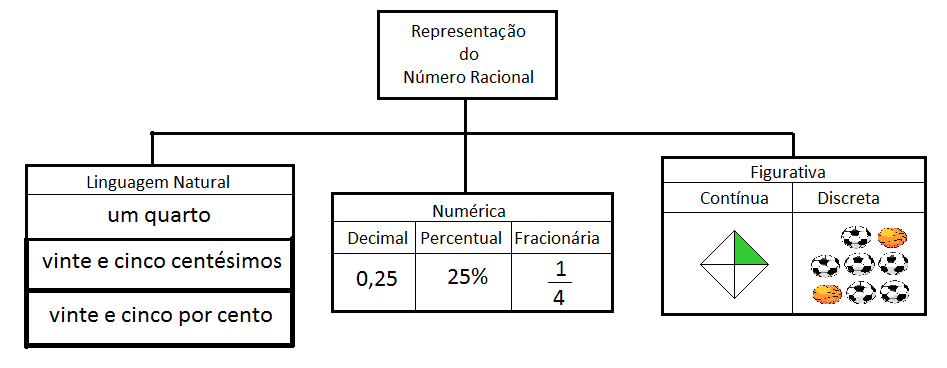
A Teoria dos Registros de Representação Semiótica-TRRS

A Teoria dos Registros de Representação Semiótica - TRRS, desenvolvida pelo psicólogo e filósofo Raymond Duval (2003), postula a importância de levar em consideração as representações semióticas ao tratarmos sobre os processos de ensino e aprendizagem em matemática. A partir da TRRS, compreendemos que para um bom aprendizado é importante que o aluno demonstre saber expressar um mesmo objeto matemático de diferentes maneiras, bem como migrar de uma representação para outra. Para Duval (2009, p. 63), ?uma aprendizagem especificamente centrada na mudança e na coordenação de diferentes registros de representação, produz efeitos espetaculares nas macro-tarefas de produção e de compreensão?. Por outro lado, ?a ausência de coordenação entre diferentes registros cria muito frequentemente uma deficiência para as aprendizagens conceituais? (DUVAL, 2009, p. 63).

Duval (2013, p. 16)afirma que ?a distinção entre os diferentes registros permite separar os dois tipos de transformações que constituem a atividade matemática: as conversões e os tratamentos?. O autor explica que, enquanto o tratamento refere-se a uma transformação interna, ou seja, ocorre no interior de um registro de representação ou sistema, a conversão diz respeito a ?uma transformação externa em relação ao registro da representação de partida? (DUVAL, 2009, p. 59).

Assim, a conversão se constitui como a mais importante das transformações relacionadas às representações e a dificuldade apresentada pelos alunos se deve ao esforço cognitivo que o indivíduo precisa empreender para migrar de uma representação a outra. É, portanto, nessa transformação externa dos registros que o indivíduo estabelece a apreensão conceitual do objeto estudado ( DUVAL, 2003).

O papel fundamental das conversões no ensino da matemática

Para Duval (2003), a ênfase dada ao aspecto matemático nos processos de ensino e aprendizagem tem relegado a conversão a um papel meramente secundário. Nesse sentido, nas palavras do autor,

a conversão intervém somente para escolher os registros no qual os tratamentos a serem efetuados são mais econômicos, mais potentes, ou para obter um segundo registro que serve de suporte ou de guia aos tratamentos que se efetuam em um outro registro (p.16).

Assim, ao olharmos o ensino e a aprendizagem apenas do ponto de vista matemático, estamos subestimando o papel fundamental, do ponto de vista cognitivo, que as conversões desempenham. Nesse contexto, Duval (2003, p. 16) explica que ?é por isso que a conversão não chama a atenção, como se se tratasse somente de uma atividade lateral, evidente e prévia à ?verdadeira? atividade matemática?.

É, contudo, no aspecto cognitivo que a conversão surge como a mais importante das transformações de representações, pois, como vimos, é esta a atividade que ?conduz aos mecanismos subjacentes à compreensão? ( DUVAL, 2003, p. 16).

Segundo Duval (2003), esta distinção entre o ponto de vista matemático e o ponto de vista cognitivo não tem sido levada em conta em boa parte das pesquisas em didática e, no próprio ensino da matemática, muitas vezes, a conversão é realizada como uma forma de tratamento, ou seja, para converter a representação de um objeto de um registro a outro, aplicam-se regras de correspondência e faz-se uma espécie de tradução.

No quadro 1, apresentamos alguns exemplos de codificação, envolvendo dois objetos matemáticos, a função afim e a fração, bem como a regra de codificação relacionada:

Quadro 1: Exemplos de codificação nas conversões

Quadro 1

Exemplos de codificação nas conversões

MELO, 2019

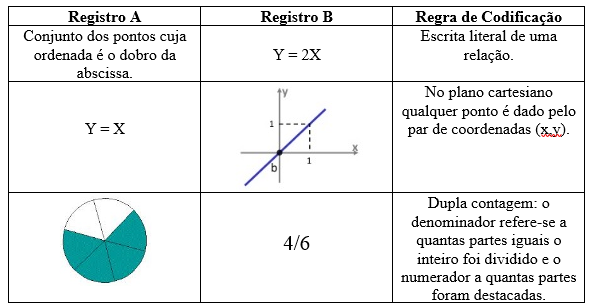
Podemos entender a codificação como um tipo de conversão muito limitada do ponto de vista cognitivo, pois não oportuniza aos estudantes o aprofundamento conceitual que uma conversão não condicionada a regras de codificação oferece.

Para Duval (2003, p. 17), a codificação gera apenas uma visão superficial baseada numa regra de correspondência entre os registros que, por sua vez, ?permite somente uma leitura pontual das representações gráficas?.

A conversão tomada como simples codificação impede o que o autor chama de ?uma apreensão global e qualitativa? ( DUVAL, 2003, p. 17). No caso, por exemplo, das conversões envolvendo as expressões algébricas e os gráficos, é absolutamente necessária esta apreensão global e qualitativa para ?extrapolar, interpolar, ou para utilizar os gráficos para fins de controle, ou de exploração, relacionados aos tratamentos algébricos? ( DUVAL, 2003, p. 17).

Os Materiais Didáticos Manipuláveis Concretos

A história dá conta de que antigos grupos humanos se valiam de riscos feitos em bastões de madeira, marcas em paredes de cavernas, nós em cordas, ossos e até pequenas pedras para ajudar a contar os seus animais e sua pequena produção agrícola ( SOARES, 2007). Pode-se dizer, portanto, que o pensamento matemático entre os primeiros homens esteve acompanhado pela utilização de objetos concretos como recursos auxiliares.

Com o aumento da produtividade e a maior complexidade exigida na contagem, instrumentos elaborados para dar suporte à atividade matemática foram surgindo, tais como o ábaco, um dos primeiros objetos confeccionados com este propósito ( MENDES, FILHO e PIRES, 2011).

Segundo Lorenzato (2006, p. 18), o material didático é definido como ?qualquer instrumento útil ao processo de ensino e aprendizagem?, enquanto que o material didático concreto pode referir-se ?ao palpável, manipulável? e ainda, numa interpretação mais ampla, incluir imagens gráficas ( LORENZATO, 2006, p. 22).

No conjunto dos materiais didáticos manipuláveis concretos, como denomina o autor, pode-se, portanto, incluir todos aqueles objetos que tocamos, sentimos e manuseamos, ou seja, desde materiais mais simples, tais como folhas de papel, massa de modelar, palitos de fósforo, bolas de isopor, até aqueles elaborados com uma explícita intenção didática, tais como o ábaco, o material dourado, o disco de frações, utilizados no sentido de construir de forma mais significativa o conhecimento sobre determinados conteúdos matemáticos.

Para Turrioni e Perez (2006, p. 61), o material manipulável concreto é de fundamental importância no ensino, pois ?facilita a observação, análise, desenvolve o raciocínio lógico e crítico, sendo excelente para auxiliar o aluno na construção de seus conhecimentos?.

Embora a relevância dos materiais manipuláveis concretos no ensino seja uma percepção recorrente na maioria dos autores que tratam do assunto, não se pode deixar de observar que tais materiais não são eficazes por si mesmos. Como afirma Pais (2001, p. 2), ao pensarmos que a aprendizagem se dará apenas porque os alunos estão interagindo de forma física com tais objetos movendo-os ou modificando-os, estaremos caindo num ?empirismo desprovido de significado?.

Neste caso, o autor destaca que o princípio do ?aprender fazendo?, que permeia a concepção de uso dos manipuláveis durante as aulas, é aplicado de forma equivocada, supervalorizando a manipulação pela manipulação em detrimento da imprescindível correlação entre a experiência com o material e a apropriação do conceito matemático envolvido ( PAIS, 2001).

Com o objetivo de discutir os aspectos matemático e cognitivo com uso de material manipulável nas conversões entre representações do número racional, realizamos um recorte no estudo original, cuja metodologia descrevemos a seguir.

3. Metodologia

A metodologia utilizada consistiu de uma pesquisa de cunho qualitativo, entendendo que ela trabalha com o ?universo de significados, motivos, aspirações, crenças, valores e atitudes, o que corresponde a um espaço mais profundo das relações, dos processos e dos fenômenos? ( MINAYO, 1994, p. 22)

Constituíram o campo de pesquisa e participantes, alunos do 8° e 9° ano do ensino fundamental de escolas da rede pública municipal do Recife, capital do estado de Pernambuco.

Utilizamos a observação participante, definida por Minayo (1994, p. 59) como uma técnica que ?se realiza através do contato direto do pesquisador com o fenômeno observado para obter informações sobre a realidade dos atores sociais em seus próprios contextos?.

No que concerne ao foco dessa pesquisa, podemos dividi-la em dois momentos: no primeiro, observamos, num experimento piloto, como os alunos realizavam as conversões utilizando quatro manipuláveis (disco de frações, régua numérica, pastilhas plásticas e material dourado adaptado); no segundo momento, concentramos nossa investigação num único material manipulável que foi escolhido a partir das observações realizadas no primeiro momento, a saber, o material dourado adaptado.

O instrumento avaliativo constou de quinze questões com quatro alternativas de resposta para cada uma delas, explorando conversões envolvendo representações numéricas, figurativas e em linguagem natural. As questões 1, 2, 6, 7, 8, 9 e 15 propunham conversões que envolviam apenas os registros simbólico-numéricos fracionário, decimal e percentual, as questões 4, 5, 10, 11, 12, 13 e 14 utilizavam registros figurativos nos enunciados ou entre as alternativas, enquanto que os registros em linguagem natural apareciam nas questões 3 e 10.

Aplicamos o instrumento avaliativo, inicialmente sem a utilização do material manipulável, na primeira semana do mês de outubro de 2018. Nesse momento, participaram dez alunos, com idades entre 13 e 14 anos, sendo seis estudantes do 9° ano e quatro do 8º ano do ensino fundamental da rede pública municipal do Recife.

A segunda aplicação do instrumento avaliativo, dessa vez com a utilização do material dourado adaptado, ocorreu na última semana de novembro de 2018. Participaram desta etapa os cinco alunos com os menores percentuais de acertos no primeiro teste.

O Material Dourado Adaptado

O material dourado foi um dos vários manipuláveis desenvolvidos pela médica e educadora italiana Maria Montessori no início do século XX. Montessori realizou experiências com crianças e criou materiais destinados à aprendizagem de conteúdos matemáticos.

Os materiais desenvolvidos por Montessori tinham como característica comum o forte apelo à percepção visual e tátil, pois acreditava que a ação sobre os objetos é que possibilitava a aprendizagem.

Para Montessori, a experiência deveria preceder qualquer formalização conceitual, já que ?nada deve ser dado à criança, no campo da matemática, sem primeiro apresentar-se a ela uma situação concreta que a leve a agir, a pensar, a experimentar, a descobrir, e daí, a mergulhar na abstração? ( AZEVEDO, 1979, p. 27).

Podemos descrever brevemente o material dourado, apresentado na figura 2, como um conjunto de pequenas peças, geralmente produzidas em madeira, que contém pequenos cubos para representar as unidades, barras que agrupam dez destes cubos para representar as dezenas, placas que agrupam dez destas barras para representar as centenas e, algumas vezes, um cubo grande com tamanho equivalente a dez placas agrupadas para representar a unidade de milhar.

Figura 2
Material dourado de Montessori
site EDUP- educação e psicopedagogia disponível em: www.edupp.com.br

Figura 2: Material dourado de Montessori

Fonte: site EDUP- educação e psicopedagogia disponível em: www.edupp.com.br

O material dourado de Montessori destina-se, principalmente, ao ensino e aprendizagem de conceitos relacionados ao sistema de numeração decimal. A compreensão do nosso sistema como uma organização de agrupamentos de dez em dez, bem como o entendimento da dinâmica de reagrupamentos de unidades realizados, sobretudo, nas operações de adição e subtração com uso dos algoritmos pode ser muito favorecidos, pois as abstrações relacionadas a estes conhecimentos passam a ter uma imagem concreta.

Chamamos o manipulável utilizado nessa pesquisa de material dourado adaptado porque realizamos algumas pequenas alterações no material original que consistiram, basicamente, em algumas marcações com pinturas de diferentes cores e inscrições de registros numéricos em sua superfície.

O material dourado adaptado é composto por três conjuntos, um para cada representação simbólico-numérica. Os conjuntos referentes às representações decimais e percentuais contêm, cada um, 1 placa, 5 barras e 10 cubos pequenos, já o conjunto das representações fracionárias, além de possuir 1 placa, 10 barras e 10 cubos pequenos, também é composto por subdivisões da placa em partes equivalentes a 1/2, 1/4 e 1/5.

Como podemos ver nas figuras 3, 4 e 5, o conjunto vermelho refere-se à representação numérica decimal, o conjunto verde à representação numérica percentual e o conjunto amarelo à representação numérica fracionária do número racional.

Figura 3
Material dourado adaptado
MELO, 2019

Figura 4
Material dourado adaptado
MELO, 2019

Figura 5
Material dourado adaptado amarelo
MELO, 2019

No material vermelho a placa representa o inteiro (1), as barras representam os décimos e os cubinhos representam os centésimos. De forma análoga, no material verde, a placa representa o total (100%) e as barras e cubinhos, respectivamente, 10% e 1%.

O verso de cada placa traz registros numéricos relativos à metade, décima parte e centésima parte do todo para cada representação, como podemos ver nas figuras 6 e 7 :

Figura 6
Verso da placa do material
MELO, 2019

Figura 7
Verso da placa do material
MELO, 2019

O material dourado amarelo, como se pode ver na figura 8, traz uma placa inteira com o registro numérico fracionário 50/100 inscrito em sua metade, blocos menores representando 1/2, 1/4 e 1/5, além das barras e os cubinhos representando, respectivamente, as frações 1/10 e 1/100.

Figura 8
Representações fracionárias no material amarelo
MELO, 2019

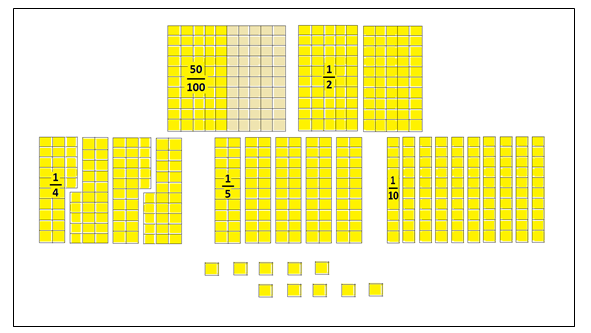
Como vimos anteriormente, o cubo pequeno do material dourado é usado, normalmente, para representar a unidade. Contudo, não poderemos subdividir o cubinho de madeira ao tratar de partes menores que a unidade. Por esta razão, encontramos, em algumas obras, a sugestão de considerar o cubo grande, que antes representava a unidade de milhar, como sendo a unidade. Com a adaptação feita passamos a considerar a placa como a unidade, permitindo demonstrações até a casa dos centésimos.

Cada placa funciona como uma espécie de malha quadriculada concreta na qual os alunos podem visualizar a relação da grandeza contínua (área pintada do todo) com a grandeza discreta (número de cubinhos considerados).

Para Duval (2011, p. 67), algumas representações semióticas podem ser classificadas como representações mistas, pois ?resultam da superposição ou da fusão de dois tipos de representações?. O autor cita como exemplo as retas com marcações de unidades tais como a reta numérica, onde observamos o registro gráfico (reta) e o numérico (números) na mesma representação.

Nesse sentido, consideramos o material dourado adaptado como um tipo de representação mista, já que, inscritas nas superfícies dos conjuntos vermelho, verde e amarelo, temos, respectivamente, os registros numéricos decimais, percentuais e fracionários. Assim, optamos por chamar de representações figurativas concretas as representações mistas elaboradas pelos alunos a partir do material dourado adaptado.

O material dourado adaptado favorece a aplicação de diferentes estratégias para a resolução das atividades de conversão propostas, dentre as quais algumas relacionadas à técnica do ladrilhamento, também conhecida como mosaico ou pavimentação do plano.

Segundo Dalcin e Alves (1999, p. 3), os chamados mosaicos do plano caracterizam-se pela cobertura de uma superfície plana feita por regiões poligonais sem deixar lacunas ou sobreposições. Esta ?pavimentação do plano? surge como ?um conjunto numerável de ladrilhos que cobrem o plano sem espaços intermediários nem sobreposições?.

O Uso do Material Dourado Adaptado na Construção de Possíveis Caminhos Resolutivos

A partir do que foi observado no experimento piloto, pudemos antever o caminho resolutivo mais utilizado em todas as conversões envolvendo representações simbólico-numéricas e figurativas propostas no instrumento avaliativo.

No quadro 2, descrevemos esta estratégia de resolução tomando como exemplo a conversão de 1/4 para a sua representação numérica decimal:

Quadro 2
Possível caminho resolutivo com o material dourado adaptado para a conversão 1/4 ? 0,25
MELO, 2019

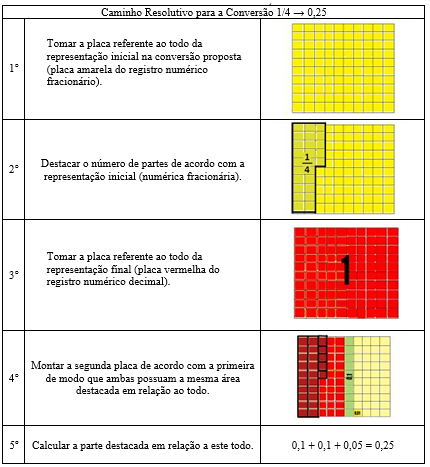
No caminho resolutivo, os alunos utilizavam as duas placas referentes às representações envolvidas no exercício de conversão, neste caso, a placa amarela das representações fracionárias e a placa vermelha das representações decimais. A primeira placa era montada de acordo com o registro inicial e a segunda era manipulada de modo que a parte destacada tivesse a mesma área que a primeira em relação ao todo. Assegurada a equivalência das áreas, restava calcular, na segunda placa, a parte destacada em relação ao todo, tomando por referência as indicações numéricas gravadas no material.

Observa-se que a estratégia deriva de uma regra de correspondência associada ao próprio material, a saber, se placas de representações diferentes têm partes destacadas equivalentes, então tais partes representam o mesmo número racional.

Assim, considerando esta relação do manipulável com sua regra de correspondência, discutimos, a seguir, os aspectos matemático e cognitivo desse tipo de resolução.

4. Análise e discussão dos resultados

A primeira aplicação do instrumento avaliativo foi realizada de forma coletiva com 10 alunos e sem a utilização do material dourado adaptado. A tabela 1 apresenta o desempenho dos alunos, destacando as questões respondidas corretamente, bem como o índice individual de acertos. Chamamos o primeiro aluno na ordem alfabética de A1, o segundo de A2, e assim por diante. As questões foram representadas pela letra Q e os acertos indicados pela letra C:

Tabela 1: Desempenho dos alunos sem o manipulável

Tabela 1

Desempenho dos alunos sem o manipulável

(MELO, 2019)

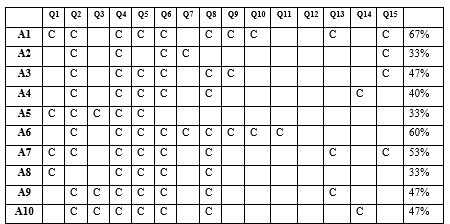
Os resultados parecem ratificar que os alunos, de fato, apresentam grandes dificuldades quando estão diante de uma atividade de conversão. Embora seja um grupo totalmente oriundo dos anos finais do ensino fundamental, apenas três alunos acertaram mais que a metade das questões propostas. Sob a perspectiva da TRRS, tal dificuldade era previsível já que ?a conversão das representações semióticas é a primeira fonte de dificuldade à compreensão em matemática? (DUVAL, 2012, p. 276).

A segunda aplicação do instrumento foi feita individualmente com 5 alunos que apresentaram baixo desempenho na primeira aplicação e com utilização do material dourado adaptado. No primeiro momento, o manipulável era apresentado ao aluno, bem como a sua utilização nos exercícios de conversão entre representações semióticas do número racional. Neste caso, estamos falando de demonstrar como usar o material dourado adaptado nestas conversões a partir da regra de correspondência a ele associada, ou seja, se placas de representações diferentes têm partes destacadas equivalentes, então tais partes representam o mesmo número racional. A tabela 2 traz os desempenhos observados nesse momento:

Tabela 2

Desempenho dos alunos com o manipulável

MELO, 2019

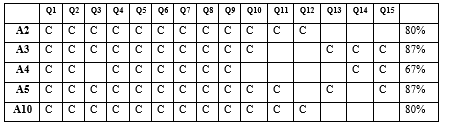
Observamos uma melhora significativa nos índices de acertos com a utilização do manipulável, o que sugere uma influência positiva da utilização deste concreto no desempenho dos alunos frente aos exercícios de conversão propostos.

Nas primeiras dez questões do instrumento avaliativo observamos um aproveitamento quase que total dos alunos. Vemos nesse dado uma importante indicação de que a regra de correspondência entre as representações aplicada com o material dourado adaptado foi de grande valia para encontrar a alternativa correta em cada exercício de conversão.

Ao utilizarem o material dourado adaptado, os alunos buscaram reproduzir, com pequenas variações, o caminho exemplificado inicialmente pelo pesquisador, ou seja, considerar a placa como sendo o todo, o inteiro ou a unidade, destacar em sua superfície a parte correspondente à representação inicial do exercício de conversão proposto utilizando as barras e os cubinhos e tomando por referência os registros numéricos em seu verso, reproduzir esta parte destacada na superfície da placa da representação final e, finalmente, calcular a representação final também tomando por referência os registros numéricos no seu verso. Esta pouca variedade de estratégias nos pareceu bastante razoável haja vista alguns limites impostos pela própria pesquisa, tais como o pouco tempo de interação dos alunos com estes materiais.

Pode-se dizer, portanto, que a estratégia mais adotada pelos alunos, que responderam corretamente as situações de conversão propostas, baseou-se, fundamentalmente, nas informações dadas pelo pesquisador ao apresentar-lhes o manipulável que deveriam utilizar e consistiu basicamente em identificar o todo e procurar deduzir, a partir deste todo, o valor das partes destacadas conforme o problema. Nesse sentido, pudemos perceber que houve uma mobilização predominante do sentido parte-todo da fração nos procedimentos de resolução destes exercícios.

Tais resultados parecem indicar que o pesquisador, ao apresentar o manipulável aos alunos, sugere um ?como utilizar? que é transformado numa regra a ser obedecida ao realizar a correspondência entre as representações envolvidas no exercício de conversão. Nesse sentido, supomos que o manipulável utilizado esteve associado àquilo que Duval (2003) chamou de regra de correspondência.

Como vimos na fundamentação teórica, as regras de correspondência são aplicadas para transformar um tipo de registro em outro, fazendo com que a conversão realizada se aproxime de uma simples codificação o que, do ponto de vista cognitivo, não seria o ideal nestes exercícios ( DUVAL, 2003).

O caminho resolutivo, descrito anteriormente, foi o mais adotado pelos alunos que não tiveram muita dificuldade para montar a representação inicial, trazida pelo enunciado da questão, utilizando a placa correspondente àquele tipo de registro, montar a placa correspondente ao tipo de registro das alternativas, de modo que a parte destacada nesta segunda placa fosse equivalente à da primeira, e, finalmente, chegar à representação final calculando a parte destacada na segunda placa em relação ao seu todo, utilizando, para tanto, as referências inscritas em seu verso.

A não obtenção da totalidade de acertos entre as questões Q1 e Q10 deveu-se a dois erros cometidos pelo aluno A4 nas questões Q3 e Q10 cuja presença das representações em linguagem natural ?cinco centésimos? e ?vinte e cinco centésimos?, respectivamente, dificultam uma aplicação direta da regra de correspondência com o manipulável, pois exige, a priori, a habilidade de relacionar este tipo de representação com os registros simbólico-numéricos inscritos no material.

Percebe-se no caminho resolutivo apresentado com o manipulável aos alunos a importância fundamental da regra de correspondência, ou seja, se placas de representações diferentes têm partes destacadas equivalentes, então tais partes representam o mesmo número racional. Portanto, podemos concluir que a utilização do manipulável e, consequentemente, desta regra foi preponderante para o crescimento dos índices de acertos nestas dez primeiras questões do instrumento avaliativo.

No entanto, é preciso muita cautela ao considerarmos este ?êxito? dos alunos na resolução das conversões propostas nestes exercícios, pois, segundo Duval (2003, p. 27), ?aquilo que de um ponto de vista matemático pode ser considerado um acerto (ou um erro) elementar não tem nenhum valor do ponto de vista cognitivo?, em outras palavras, ?um sucesso matemático não corresponde a um sucesso cognitivo?.

Assim, para estas questões do instrumento avaliativo, podemos apenas concluir que, do ponto de vista matemático, a utilização do manipulável se mostrou bastante eficiente como apoio à resolução das conversões, contudo, do ponto de vista cognitivo, ainda não se pode dizer que o uso do material dourado adaptado teve contribuições a dar aos alunos.

Isto porque, para Duval (2012, p. 273), a ?codificação?, ou seja, a ?transcrição de uma representação em outro sistema semiótico diferente daquele em que é dado inicialmente? é caracterizada pela utilização de regras de correspondência que resultam numa série de substituições. Como vimos, na fundamentação deste trabalho, tais mudanças de registros, baseadas na codificação, são pobres do ponto vista cognitivo, pois não precisam, necessariamente, estar acompanhadas de nenhuma apreensão conceitual referente ao objeto matemático envolvido (DUVAL, 2012).

Portanto, ao analisarmos a utilização do material dourado adaptado e a regra de correspondência associada a este manipulável, precisamos ter bastante cuidado para não confundirmos sua eficiência matemática com sua eficiência cognitiva.

Nas cinco questões finais, percebemos uma queda de desempenho dos alunos. Podemos relacionar essa diminuição de acertos nas conversões propostas ao fato de que, a partir de Q11, os exercícios requerem conhecimentos e habilidades para além da simples aplicação da regra de correspondência associada ao material dourado adaptado.

Duval (2012), ao criticar a ênfase nas atividades de tratamento em detrimento das atividades de conversão no ensino, explica que:

é evidente que esta ausência, que não leva em conta a coordenação de registros, não é por acaso ou por negligência. A falta quase completa de regras que pudessem contribuir para a atividade cognitiva de conversão poderia ser suficiente para explicar (p. 285).

Assim, a utilização de manipuláveis como o material dourado adaptado na mediação entre diferentes registros de um número racional, se por um lado, favorecem o surgimento de regras de correspondência que serão utilizadas pelos alunos, o que para a TRSS não é o ideal, por outro, podem, diante dessa ?falta quase completa de regras?, romper com a imobilidade dos alunos diante de atividades de conversão, oferecendo-lhes um caminho e colocando-os em movimento (DUVAL, 2012, p. 285).

5. Considerações finais

A pesquisa indicou que, embora o uso do manipulável nos exercícios de conversão entre representações semióticas do número racional apresente limites, tais como a ênfase no significado parte-todo, em detrimento de outros sentidos da fração, e o uso de regras de correspondência (codificação) no caminho resolutivo, há evidências de que a inserção do concreto como mediador nestas atividades, além de pôr os alunos em movimento no sentido das resoluções, foi importante para o aumento significativo de acertos nas questões propostas.

A necessidade de explorar a pluralidade de representações vem do fato de que nenhuma representação isolada dá conta do todo do objeto, já que as representações são sempre parciais em relação ao que representa, pois ?é enganosa a ideia de que todos os registros de representações de um mesmo objeto tenham igual conteúdo ou que se deixem perceber uns nos outros? ( DUVAL, 2003, p.31). Seja qual for a representação semiótica escolhida, esta imporá sempre ?uma seleção de elementos significativos ou informacionais do conteúdo que representa? ( DUVAL, 2012, p. 280).

Ao utilizarmos os materiais manipuláveis no ensino dos números racionais, incluímos um outro tipo de registro, que, no âmbito desta pesquisa, chamamos de representações figurativas concretas, tornando acessível aos alunos, portanto, a percepção de outros elementos relacionados ao objeto matemático em questão.

Escolhemos o exercício da conversão entre representações semióticas para a observação e análise da utilização das representações figurativas concretas produzidas com o manipulável por entender, a partir da TRRS, que este tipo de transformação é o primeiro e grande obstáculo à compreensão em matemática, mas, por outro lado, com relação à aprendizagem, ?desempenha um papel essencial na conceitualização? ( DUVAL, 2012, p. 277).

A utilização do manipulável ofereceu um caminho inicial e permitiu que alunos com desempenho muito baixo na primeira aplicação do instrumento avaliativo, pudessem responder corretamente a maior parte das questões.

Contudo, o caminho resolutivo para realizar as conversões, apresentado junto com o material dourado adaptado aos alunos, parece-nos estar baseado naquilo que Duval (2003) chamou de regra de correspondência ou codificação. Porém, acreditamos que a complexidade envolvida na montagem das placas e as observações proporcionadas pelas representações figurativas concretas podem justificar futuros estudos que, mais que os indícios percebidos e discutidos nesta pesquisa, possam apontar a relevância de recursos dessa natureza na apreensão conceitual dos objetos matemáticos.

Enfim, entendemos que as representações figurativas concretas, como vimos no caso do material dourado adaptado, podem cumprir uma importante função enquanto representações auxiliares e, portanto, de transição, no exercício das conversões. Contudo, acreditamos que tal abordagem no ensino da matemática será bem sucedida se tais representações ?são abandonadas pelos próprios alunos logo que eles compreendem, pois sua utilização lhes parece um procedimento longo e custoso? ( DUVAL, 2011, p. 130).

O manipulável, portanto, deve ser visto como um valioso recurso didático, podendo ser utilizado como um ponto de partida no ensino dos objetos matemáticos e sempre buscando fomentar a interiorização de representações que enriqueçam a capacidade de abstração dos alunos. Nesse sentido, os alunos devem, na sequência, ser capazes de criar suas próprias estratégias resolutivas, o que, do ponto de vista cognitivo, é o que se espera.

Esperamos que o estudo empreendido possa ter sua contribuição no campo do ensino da matemática, sobretudo se pudermos usar suas conclusões para o enriquecimento da prática docente no que tange à utilização de recursos dessa natureza durante as aulas.

6. Referências

AZEVEDO, E. D. M. Apresentação do trabalho matemático pelo sistema montessoriano. In: Revista de Educação e Matemática, n. 3, 1979 (p. 26-27).

BEHR, M. J; LESH, R.; POST, T. e SILVER, E. (1983). Rational number concepts. In: LESH, R. & LANDAU, M. (Ed.), Acquisition of mathematics concepts and processes. New York: Academic Press, p. 91-126.

BRASIL. Secretaria de Educação Fundamental. Parâmetros curriculares nacionais:Matemática / Secretaria de Educação Fundamental. Brasília: MEC / SEF, 1998.

DALCIN, M; ALVES, S. Mosaicos no plano. Revista do Professor de Matemática, v. 40, p. 3-12, 1999.

DUVAL, R. Registros de representações semióticas e funcionamento cognitivo da compreensão em matemática. In: MACHADO, S. D. A. Aprendizagem em matemática: Registros de representação semiótica. São Paulo: Papirus Editora, 2003, p.11-33.

__________.Semiósis e pensamento humano: Registros semióticos e aprendizagens intelectuais. Tradução Lênio Fernandes Levy e Marisa Rosâni Abreu da Silveira. 1. Ed. São Paulo: Livraria da Física, 2009. (Fascículo I).

__________Ver e ensinar a matemática de outra forma: entrar no modo matemático de pensar: os registros de representações semióticas/organização Tânia M. M. Campos; (tradução Marlene Alves Dias) Raymond Duval. São Paulo: PROEM, 2011.

___________ Registros de representação semiótica e funcionamento cognitivo do pensamento. Revista Eletrônica de Educação Matemática ? Revemat, Florianópolis, v.7, n.2, p.266-297, 2012. Disponível em: http://dx.doi.org/10.5007/1981-1322.2012v7n2p266

__________. Entrevista: Raymound Duval e a Teoria dos Registros de Representação Semiótica. Revista Paranaense de Educação Matemática - RPEM, Campo Mourão, v.2, n.3, jul-dez. 2013. Entrevista concedida a FREITAS, J. L. M. de; REZENDE, V.

FERNANDES, N. R.; BELLEMAIN, P.M.B.; LIMA, J.M.F.; TELES, R.A.M. . Número racional e seus diferentes significados, Anais do 2º SIPEMAT, pp.1-22, 2008. Disponível em http://www.gente.eti.br/lematec/CDS/SIPEMAT08/artigos/CO-134.pdf Acesso em: 01/08/2016.

GITIRANA, V; CARVALHO, J. A matemática do contexto e o contexto na matemática. In: João Bosco Pitombeira Fernandes de Carvalho (Coord.), Coleção Explorando o Ensino, Matemática, v.17, Brasília: Ministério da Educação, Secretaria de Educação Básica, 2010, p.69-90.

______. A metodologia de ensino e aprendizagem nos livros didáticos de matemática. In: João Bosco Pitombeira Fernandes de Carvalho (Coord.), Coleção Explorando o Ensino, Matemática, v.17, Brasília: Ministério da Educação, Secretaria de Educação Básica, 2010.

KIEREN, T. E. Personal Knowledge of rational numbers: its intuitive and formal developmente. In: J. Hiebert and M. Behr (eds): Number Concepts and Operations in the Middle Grades. Hillsdale, New Jersey: Erlbaum, 1998.

LORENZATO, S. A. Laboratório de ensino de matemática e materiais didático manipuláveis. In: LORENZATO, Sérgio (org.). O Laboratório de ensino de matemática na formação de professores. Campinas: Autores Associados, 2006.

MANDARINO, M. C. F. ?Números e operações?, in João Bosco Pitombeira Fernandes de Carvalho (Coord.), Coleção Explorando o Ensino, Matemática, v.17, Brasília: Ministério da Educação, Secretaria de Educação Básica, 2010, p. 97-134.

MENDES, I. A.; FILHO, A. S.; PIRES, M. A. L. M. Ábaco. In: MENDES, Iran Abreu (Org.). Práticas matemáticas em atividades didáticas para os anos iniciais. São Paulo: Livraria da Física, 2011. (77-94).

MINAYO, M. C. Pesquisa Social:Teoria, método e criatividade. 21 ed. Petrópolis, RJ: Vozes, 1994.

NUNES, T., BRYANT, P., PRETZLIK, U. & HURRY, J. The effect of situations on children?s understanding of fractions.Trabalho apresentado no encontro da British Society for Research on the Learning of Mathematics. Oxford, June, 2003.

OHLSSON, S. Mathematical Meaning and Applicational Meaning in the Semantics of fractions and Related Concepts. In: HERBERT, J. e BEHR, M. Numbers concepts and operations in the middle grades. Reston, VA: National Council of Teachers of Mathematics, p. 53-92, 1989.

PAIS, L. C. Uma análise do significado da utilização de recursos didáticos no ensino da geometria, 2001. Disponível em: http://www.ufrrj.br/emanped/paginas/conteudo_producoes/docs_23/analise_significado.pdf. Acesso em: 01/08/2016.

SOARES, K. M. Fundamentos e história da matemática. Indaial: Asselvi, 2007.

TURRIONI, A. M. S. O laboratório de educação matemática na formação inicial de professores. Dissertação de Mestrado. UNESP, Rio Claro, 2004.

TURRIONI, A. M. S.; PEREZ, G. Implementando um laboratório de educação matemática para apoio na formação de professores. In: LORENZATO, S. Laboratório de Ensino de Matemática na formação de professores. Campinas: Autores Associados, 2006. p. 57-76.

Autor notes

Ligação alternative

http://www.revistasbemsp.com.br/index.php/REMat-SP/article/view/328/pdf (pdf)