Resumo: A história da matemática oferece diversos recursos didáticos e estratégias para o ensino de matemática, contribuindo para a construção do conhecimento matemático. Dentre esses recursos disponíveis, destacam-se os instrumentos matemáticos contidos em antigos tratados, em particular, os situados nos séculos XVI e XVII. O Via Regia ad Geometriam é um desses textos, que foi publicado na língua latina em 1569, pelo francês Petrus Ramus, traduzido para o inglês e publicado por William Bedwell, em 1636. Esse documento, que trata da “arte de medir bem”, traz um instrumento utilizado por agrimensores da época, denominado de báculo. A descrição da fabricação e de diferentes situações de uso do báculo, para medição de distâncias (comprimentos) e alturas, é apresentado no capítulo nove do tratado. Em vista disso, o presente artigo tem a finalidade de apresentar os conhecimentos matemáticos com base em uma situação proposta por Petrus Ramus, para o uso de seu báculo, relacionada à medição de profundidade. Assim, utilizou-se uma metodologia qualitativa documental, a partir da tradução, compreensão (histórica e matemática) e discussão do excerto, que direcionaram a buscar potencialidades didáticas do uso do báculo para essa situação. No decorrer do estudo, percebeu-se que, para essa situação específica, o autor nomeia a profundidade de altura reversa (Eversa altitudo), ou seja, ele a considera como uma altura abaixo do solo, voltada para medição de poços, buracos fundos e rios. Com relação aos conceitos matemáticos advindos da aplicação dessa situação, percebe-se que perpendicularidade, paralelismo, propriedades do triângulo retângulo, semelhança de triângulos, dentre outros, são utilizados no manuseio do báculo e que ambos podem ser direcionados ao desenvolvimento de algumas habilidades da Base Nacional Comum Curricular (BNCC) no Ensino Fundamental. Entretanto, considera-se que, após uma medição real de uma profundidade, por meio do instrumento, outros conceitos podem ser percebidos e agregados às potencialidades didáticas, visando, assim, estabelecer uma articulação entre a história e o ensino de matemática.
Palavras-chave: Procedimento de Medição, Báculo de Petrus Ramus, Via Regia ad Geometriam.
Abstract: The history of mathematics offers several didactic resources and strategies for mathematics teaching, contributing to the construction of mathematical knowledge. Among these available resources, the mathematical instruments contained in old treaties are stand out those situated in the 16th and 17th centuries. The Via Regia ad Geometriam, is one of those texts, which it was published in Latin in 1569, by the French Petrus Ramus, translated into English and published by William Bedwell, in 1636. This document, which deals with the “art of measuring well”, brings an instrument used by surveyors of the time, called baculum. The description of the manufacture and different situations of use of baculum, for measuring distances (lengths) and heights, it is presented in chapter nine of the treatise. In this sense, this article aims to present mathematical knowledge based on a situation proposed by Petrus Ramus, for the use of his baculum, related to depth measurement. Thus, a qualitative documentary methodology was used, based on translation, comprehension (historical and mathematical) and discussion of the excerpt, which guided the search for didactic potentialities of using the baculum for this situation. During the study, it was noticed that, for this specific situation, the author names the depth as reverse height (Eversa altitudo), in another words, he considers it to be a height below the ground, focused on measuring wells, deep holes and rivers. With regard to the mathematical concepts arising from the application of this situation, it is clear that perpendicularity, parallelism, properties of the right triangle, similarity of triangles, among others, are used in the handling of the baculum and that both can be directed to the development of some skills of the Base National Common Curriculum (BNCC) in Elementary Education. However, it is considered that, after a real measurement of a depth, using the instrument, other concepts can be perceived and added to the didactic potentialities, aiming, thus, to establish an articulation between history and the teaching of mathematics.
Keywords: Measurement Procedure, Petrus Ramus’ Baculum, Via Regia ad Geometriam.
Resumen: La historia de las matemáticas ofrece varios recursos didácticos y estrategias para enseñar matemáticas, contribuyendo a la construcción del conocimiento matemático. Entre estos recursos disponibles, destacan los instrumentos matemáticos contenidos en tratados antiguos, en particular los ubicados en los siglos XVI y XVII. Via Regia ad Geometriam es uno de estos textos, que fue publicado en lengua latina en 1569, por el francés Petrus Ramus, traducido al inglés y publicado por William Bedwell, en 1636. Este documento, que trata sobre el "arte de medir bien", trae un instrumento utilizado por los topógrafos de la época, llamado báculo. La descripción de la fabricación y las diferentes situaciones de uso del báculo, para medir distancias (longitudes) y alturas, se presenta en el capítulo nueve del tratado. En vista de esto, el presente artículo tiene como objetivo presentar el conocimiento matemático basado en una situación propuesta por Petrus Ramus, para el uso de su báculo, relacionada con la medición de profundidad. Por lo tanto, se utilizó una metodología documental cualitativa, basada en la traducción, la comprensión (histórica y matemática) y la discusión del extracto, que guió la búsqueda de las potencialidades didácticas del uso del báculo para esta situación. Durante el estudio, se notó que, para esta situación específica, el autor nombra la profundidad de la altura inversa (Eversa altitudo), es decir, la considera una altura debajo del suelo, destinada a medir pozos, agujeros fondos y ríos. Con respecto a los conceptos matemáticos que surgen de la aplicación de esta situación, está claro que la perpendicularidad, el paralelismo, las propiedades del triángulo rectángulo, la similitud de los triángulos, entre otros, se utilizan en el manejo del báculo y que ambos pueden dirigirse al desarrollo de algunas habilidades de la Base National Common Curriculum (BNCC) en Educación Primaria. Sin embargo, se considera que, después de una medición real de la profundidad, utilizando el instrumento, se pueden percibir y agregar otros conceptos a las potencialidades didácticas, con el objetivo de establecer una articulación entre la historia y la enseñanza de las matemáticas.
Palabras clave: Procedimiento de medición, Báculo de Petrus Ramus, Via Regia ad Geometriam.
Artigos Científicos
O báculo de Petrus Ramus e seu uso para medição de profundidade
Petrus Ramus’ baculum and its use for depth measurement
El báculo de Petrus Ramus y su uso para la medición de profundidad
Recepção: 29 Abril 2020
Aprovação: 20 Julho 2020
Publicado: 02 Setembro 2020

Este trabalho está sob uma Licença Creative Commons Atribuição-NãoComercial 4.0 Internacional.
A história da matemática é constitucionalizada como uma área de conhecimentos e pesquisa, que possui algumas vertentes de estudos, das quais uma delas tenta fazer a articulação da história da matemática com a educação matemática. Essa vertente estuda o caráter epistemológico e didático-pedagógico, implementando recursos e estratégias a serem usados na construção do conhecimento matemático, tendo por base uma historiografia atualizada (SAITO, 2013). Esses preceitos estão amparados na construção de interfaces entre história e ensino de matemática, que utiliza textos históricos, pois, segundo Pereira e Saito (2019a, p. 345), essa utilização “é fundamental para a realização dos estudos que culminam nas atividades para a sala de aula”.
Dessa forma, os objetos estudados na interface entre história e ensino de matemática partem do diálogo entre o historiador e o educador matemático, que
tem por base um documento histórico, que pode ser um texto ou excerto de um texto, ou ainda um instrumento, um monumento, uma foto, uma imagem, uma figura, um vídeo, entre muitos outros. É a partir da escolha consciente do documento histórico, ou do seu consequente estudo e análise, que o diálogo tem início (PEREIRA; SAITO, 2019a, p. 346).
Dentre os documentos interessantes, neste estudo, foi escolhido o tratado Via Regia ad Geometriam, publicado em latim no ano de 1569, cujo título original era Arithmeticae libri duo: geometriae septem et viginti, mas, em 1636, foi traduzido e publicado em inglês por Bedwell (1561-1632), em Londres, sob o título de Via Regia ad Geometriam – The way to geometry. No frontispício, é notório a quem se destinava o documento e sua necessidade, pois era “necessário e útil, para astrônomos, engenheiros, geógrafos, arquitetos, medidores de terras, carpinteiros, marinheiros, pintores escultores, e outros...” (RAMUS, 1636, frontispicio). Conforme Pereira e Saito (2019a, p. 349):
Esse documento, que trata da “arte de medir bem” (RAMUS, 1636, p. 1), tal como se consagrou nos estudos medievais, organiza os conhecimentos da geometria prática dando-lhe uma feição mais sistemática. O seu conteúdo é distinto daquele encontrado nos tratados de geometria especulativa, como aquela que se encontra em Elementos de Euclides, por estar orientado para finalidades práticas (...).
Organizado em 27 livros, o Via regia ad geometriam traz, em seu nono livro, um tratamento para a medição de linhas retas por meio de triângulos retângulos semelhantes, ou seja, ele apresenta várias maneiras de medir “linhas retas” por meio de um instrumento matemático denominado “báculo”. Este servia para a medição de grandes distâncias como altura, largura e comprimento.
O uso do báculo era diversificado pelos artesãos e trabalhadores do período, podendo medir comprimento de terras pelos agrimensores medievais, altura de castelos pelos arquitetos, largura de um objeto até outro pelos engenheiros e a distância de um barco até uma ilha pelos marinheiros (SAITO; PEREIRA, 2019).
Embora Ramus (1636) traga a descrição da fabricação e de diferentes situações de uso do báculo para medição de distâncias (comprimentos) e alturas[3], neste estudo, será explorado os conhecimentos matemáticos presentes na situação que envolve a medição de profundidade por meio do instrumento, relacionando-os com as habilidades e os objetos de conhecimento, delimitados pela BNCC.
O estudo se baseou na metodologia qualitativa quanto ao formato de abordagem do problema, exploratória em relação ao ponto de vista de seus objetivos, e documental no que se refere a coleta de dados. A escolha da pesquisa documental se deu a partir da realização da tradução e uma análise longitudinal do excerto do tratado de Petrus Ramus, Via Regia ad Geometriam – The way to geometry, versão de 1636. Percebe-se que há uma diferença entre pesquisa documental e pesquisa bibliográfica, pois
A diferença essencial entre ambas está na natureza das fontes. Enquanto a pesquisa bibliográfica se utiliza fundamentalmente das contribuições dos diversos autores sobre determinado assunto, a pesquisa documental vale-se de materiais que não recebem ainda um tratamento analítico, ou que ainda podem ser reelaborados de acordo com os objetos da pesquisa (GIL, 2002, p. 45).
Essa diferença é retratada pela escolha da fonte de estudo, um tratado do século XVI pouco conhecido nos campos da história da matemática e da educação matemática. Embora esteja direcionada a uma tradução, do francês para o inglês, segundo Silva (2018, p. 41), se configura numa fonte documental primária, pois ela está sendo utilizada pelo educador matemático, e não pelo historiador, ao “propor sua aplicação em sala de aula, pois ele será sua fonte de conhecimento e o principal material utilizado”.
Nesse sentido, o estudo apoiou-se na definição de pesquisa documental proposta por Kripka, Scheller e Bonotto (2015, p. 58) que relata como
aquela em que os dados obtidos são estritamente provenientes de documentos, com o objetivo de extrair informações neles contidas, a fim de compreender um fenômeno; é um procedimento que se utiliza de métodos e técnicas para a apreensão, compreensão e análise de documentos dos mais variados tipos; é caracterizada como documental quando essa for a única abordagem qualitativa, sendo usada como método autônomo
Dessa forma, o artigo versa, a partir de uma pesquisa documental, apresentar os conhecimentos matemáticos da situação relacionada à medição de profundidade por meio da utilização do báculo de Petrus Ramus, como uma forma de incorporar a história da matemática na educação básica e/ou formação de professores.
O báculo aparece no Via regia ad geometriam das páginas 113 a 135 (22 páginas no total), contendo várias maneiras de medir “linhas retas” por meio de um instrumento matemático. São, ao todo, 17 seções que trazem a fabricação, observações de uso, situações de medição de comprimentos (distâncias), alturas e profundidade. No quadro 1, é apresentada uma síntese.
Síntese do conteúdo do capítulo nono de Via regia ad geometriam (1636).
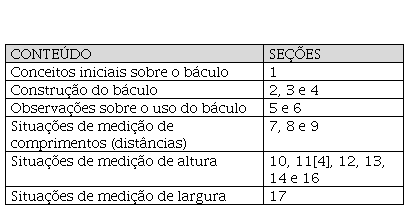
Fonte: Elaborado pelos autores.
O báculo, descrito por Ramus (1636), era composto por seis elementos, sendo duas hastes, que denominamos de indicador e tranversal, sobrepostas em um formato de cruz; três tubos, que chamamos de aletas e um cursor (Figura 1). De acordo com Saito e Pereira (2019. p. 35), “são duas as partes principais desse instrumento: o Indicador ou Bastão que é a parte maior ou mais longa e a Tranversal, que é a menor e a mais curta”. Ramus (1636) relata que o comprimento do indicador é o dobro da tranversal, somada com 1/10 de sua parte.
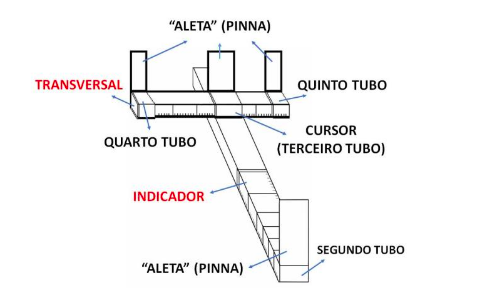
Figura 1
Partes do Báculo de Petrus Ramus
Elaborada pelos autores
Em relação às outras partes do báculo, temos aletas como sendo tubos cilíndricos, que ficam sobre uma mesma altura, por conta da linha óptica, dando um campo de visão apropriado. Além disso, temos um cursor, com um formato de tubo retangular, que foi criado com a necessidade de fazer a transversal deslizar sobre o indicador, para cima e para baixo. Como afirma Saito e Pereira (2019, p. 53):
Contudo, a Transversal se moverá mais convenientemente, por si só, para cima e para baixo, em tubos de bronze e, sobre o Indicador, para o alto ou para baixo, em ângulo reto, tocando um ao outro de tal modo que a boca alternada de uma [das hastes] possa tocar o lado da outra [haste]. O terceiro tubo deve ser movido ou deslizado para cima e para baixo, de uma extremidade da Transversal para a outra, e, desse modo, pode ser chamado Cursor. O quarto e o quinto tubos, fixos e imóveis, são colocados nas extremidades da Transversal.
Ressaltamos que a extremidade superior de cada cursor irá se equiparar a um ponto. Os três tubos estão alocados, ali, para assegurar que o raio visual seja devidamente posicionado, garantindo a precisão da medida. Ademais, o posicionamento é dado pela linha óptica, que pode ser conseguido pelo alinhamento das extremidades das aletas (PEREIRA; SAITO, 2019a).
Destacamos que, no tratado, Ramus (1636) não traz uma figura do báculo especificando suas partes e tampouco descreve o tipo de material proposto para a construção do báculo, ele apenas instrui, em etapas, os passos que devem ser seguidos para sua construção.
Para a utilização do báculo, Ramus (1636) traz algumas observações sobre seu uso, tais como postura e posicionamento do medidor em relação ao báculo. Veja:
Primeiro, uma distância justa, pois a visão não é infinita. Em segundo lugar, que um olho esteja fechado, pois a faculdade óptica transmitida por ambos os olhos em um [só olho] mira de modo mais certeiro; e o instrumento é mais apropriadamente aplicado e ajustado ao osso da bochecha do que em qualquer outro lugar [do rosto], pois aqui é como se o olho fosse o centro do círculo, em que a Transversal está inscrita. Em terceiro lugar, as mãos devem estar firmes porque, se elas tremerem, a proporção da Geodésia será certamente problemática e incerta. Por último, o lugar da posição [que deve estar o observador] é a do meio do pé (RAMUS, 1636, p. 117 apud SAITO e PEREIRA, 2019, p. 24 e 25).
Com relação à medição de determinadas distâncias, é necessário que o báculo esteja disposto de modo que a transversal preencha o comprimento ou a altura do que se quer mensurar. Nesse sentido, Ramus (1636) traz duas observações:
5. Se a visão passa do começo de uma haste, ela passa ao final da outra. E uma haste é perpendicular à grandeza a ser medida, [e] a outra [é a ela] paralela (RAMUS, 1636, p. 117 apud SAITO e PEREIRA, 2019, p. 25).
6. O comprimento e a altura têm uma medida tripla. O primeiro e o segundo tipo de medida requerem apenas uma distância e está admitindo uma extensão de um deles para a terceira proporcional. O terceiro [tipo requer] duas distâncias, e tal é a extensão da largura (RAMUS, 1636, p. 118 apud SAITO e PEREIRA, 2019, p. 26).
Não é interesse dos pesquisadores expor, neste artigo, todas as situações de uso do báculo trazidas por Ramus (1636) em seu tratado. Entretanto, salienta-se que, para realização das medidas, requer-se a participação de, pelo menos, três pessoas, sendo duas para o posicionamento e sustentação do báculo e a outra para o registro de cálculos (PEREIRA; SAITO, 2019b). A seguir, iremos detalhar a seção 11 que traz a medição da profundidade de um poço, utilizando o báculo.
A situação descrita, a seguir, é apresentada no 11o problema exposto no tratado, que está inserido na compilação de seis situações do uso do báculo, que serve para medir alturas[5]. Entretanto, no decorrer da descrição da situação, Ramus (1636) ressalta que a altura mencionada pode se diferenciar em dois tipos: aquela que está acima do solo e outra abaixo do solo. Esta última ele denomina como altura reversa:
Eversa altitudo, uma altitude reversa (Reversed, H), é aquela a que chamamos profundidade, que na realidade não é outra coisa, no sentido dos Geômetras, senão a altura virada às avessas, ou como dizemos com os calcanhares para cima. Pois, fora da altura encontrada suprimindo-se aquela que está acima do solo, permanecerá a altura ou profundidade de um poço (RAMUS, 1636, p.125, tradução nossa).
Perceba que essa altura, chamada de altura reversa, é o que relacionamos, hoje, como profundidade, que, na época, era geralmente encontrada em poços, buracos fundos e rios. Nesse sentido, é notória a utilização do báculo em uma aplicação de situação real, presente no cotidiano de muitos agrimensores medievais do período, servindo como um grande recurso a ser usado.
Desse modo, a situação estudada é enunciada da seguinte forma: “se a visão, a partir do início do Indicador, estiver paralela à altura, [então], assim como o segmento da transversal está para o segmento do indicador, assim o comprimento dado estará para a altura procurada”[6] (RAMUS, 1636, p. 124-125, tradução nossa).
Ao observarmos a Figura 2, percebemos que é feita uma esquematização com segmentos, para o entendimento do enunciado. De uma maneira mais objetiva, na primeira parte da situação, Ramus (1636) se refere à visão do observador, quando ele se posiciona no começo do indicador (SAITO; PEREIRA, 2019). Essa visão fica em um campo visual definido, que é iniciado no ponto I e é tida como um segmento de reta () , no qual o indicador estaria inserido nela, sendo paralela a uma das alturas (segmento ), que tem a mesma medida da grandeza (segmento )a ser achada.
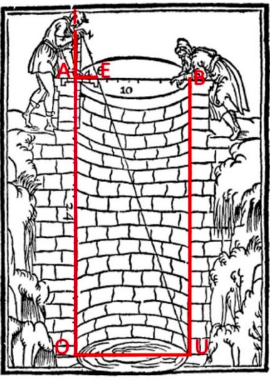
Figura 2
Esquema matemático da situação de medição de profundidade.
Imagem adaptada de Ramus (1636, p. 125).
Dessa forma, Ramus (1636) dá uma noção de posicionamento do báculo, podendo ser disposto de modo que o Indicador fique posicionado perpendicularmente à grandeza que vai ser preenchida pela Transversal, ou seja, sendo (o segmento do Indicador) e (a grandeza preenchida pela Transversal), então , uma vez que, na construção do báculo, a transversal é perpendicular ao indicador.
Na segunda parte do enunciado do problema, Ramus (1636) estabelece uma relação entre as medidas das partes do báculo com grandezas, tais como a distância (comprimento) e a altura que se quer medir. Logo, enfatizamos que a relação descrita, na situação, remete ao uso da proporção, que, por sua vez, usa conceitos de razão e o processo com operações aritméticas para a finalização da medição.
Após o enunciado da situação, Ramus (1636) traz uma explicação de como se deve proceder para realizar a medição da profundidade de um poço com seu báculo:
Seja 5 partes o segmento da transversal ae, 13 o segmento do Indicador ei, 10 pés o diâmetro do poço (que agora vale para o comprimento), que no topo é suposto igual àquele no fundo. A altura oposta, pela [sessão] 12 [do Livro] vii, e pela regra de três, será 26 pés (RAMUS, 1636, p. 125–126, tradução nossa).
Na primeira parte da explicação, Ramus (1636) traz alguns valores numéricos já definidos, como a medida da transversal, do indicador e o diâmetro do poço. Para definir a medida do comprimento (), Ramus (1636) utiliza o valor encontrado na medição do diâmetro do poço. Ressaltamos que, embora ele não enfatize a forma que obtém o comprimento (), esquematizamos, na Figura 3, uma noção de formação de um retângulo com as alturas reversas (segmentos e ), o diâmetro do poço () e o comprimento (). Sabemos, por definição, que o retângulo possui lados opostos congruentes, dessa maneira, temos que o comprimento () e o diâmetro () são lados do retângulo ABOU que satisfazem a premissa dita anteriormente e, portanto, temos que .
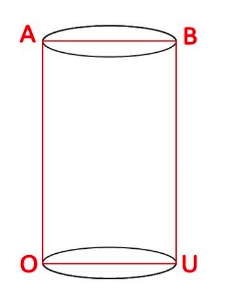
Figura 3
Esquema matemático das marcações no poço.
Elaborada pelos autores.
No que se refere ao esquema mobilizado ao se posicionar o báculo e às notações da matemática moderna, juntamente com a descrição de Ramus (1636), é denominada a medida da ponta da extremidade da Transversal até o encontro com o cursor, o segmento da Transversal ( Partes)e a medida da ponta do Indicador até o cruzamento com a Transversal, como o segmento do Indicador , conforme podemos ver na Figura 4.
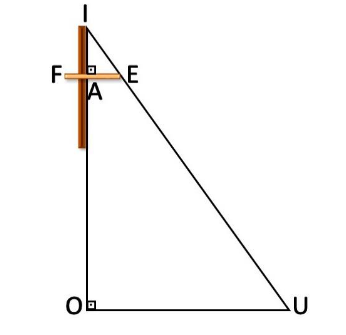
Figura 4
Esquema matemático na formação de triângulos.
Elaborada pelos autores.
Ainda, na Figura 4, com o prolongamento do segmento do indicador até o ponto O, que se encontra no fundo do poço, temos a formação do segmento . Partindo do ponto I, estendendo até o ponto U, passando pelo ponto E, temos a formação do segmento . Com essas construções, temos a criação de dois triângulos retângulos: e , que, pelo caso (Ângulo – Ângulo – Ângulo), são semelhantes[7], uma vez que , é um ângulo comum, e, assim, seus lados têm as medidas proporcionais.
Partindo do conceito de semelhanças de triângulos, temos a concretização do que é dito no enunciado, cujo segmento da transversal está para o segmento do indicador, assim como o comprimento dado está para a altura procurada (profundidade). É interessante ressaltar que Ramus (1636), em uma nota de rodapé, indica a seção 12, do livro 7, do seu tratado, que está relacionada aos conceitos de proporcionalidade entre triângulos[8] e, portanto, temos o desenvolvimento do cálculo:
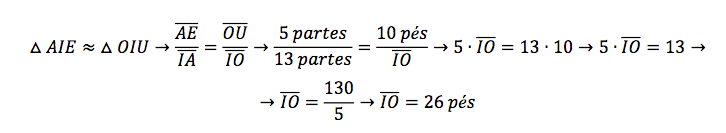 [*]
[*]Com a última parte da explicação, Ramus (1636) faz uma consideração a respeito da medida da altura: “e a verdadeira altura (ou profundidade) permanecerá; como se aquele segmento de 13 partes fosse de até 2 pés, a altura procurada seria 24 pés” (RAMUS, 1636, p. 126, tradução nossa). Com isso, percebemos que a medida encontrada, no segmento , não é a altura procurada, pois é formado por mais dois segmentos e um deles é a medida do segmento do Indicador. Assim, no esquema da Figura 5, podemos ver que:
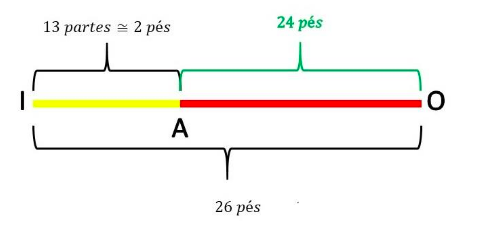
Figura 5
Esquema de segmentos.
Elaborada pelos autores.
Logo, a medida da profundidade será dada através da subtração do minuendo (segmento pelo subtraendo (segmento do indicador como podemos ver: Como a unidade de medida, para os valores encontrados, é em pés, Ramus (1636) faz uma equivalência, dizendo que 13 partes corresponderia a 2 pés, ele não explicita como é feita essa conversão, já que, para realizar qualquer operação aritmética com medidas, elas devem estar na mesma unidade e, a partir disso, concluímos que a medida da profundidade procurada é , como podemos ver na Figura 5.
Ao utilizar o báculo, percebe-se que o processo de medição é dado em etapas, sendo a primeira com o posicionamento do instrumento e a segunda com o uso do conhecimento matemático na realização dos cálculos. Desta última etapa, há o surgimento de alguns elementos matemáticos, que podem ser adaptados pelo professor para a sala de aula, implementando o ensino, tornando-o interdisciplinar.
Muitos elementos matemáticos, advindos da aplicação da medição de profundidade, estão direcionados, na sua maioria, ao ensino da geometria dos anos finais do ensino fundamental. Pode-se elencar, pelo menos, cinco deles: ângulos, elementos de uma circunferência (diâmetro), perpendicularidade, paralelismo, propriedades do triângulo retângulo, semelhança de triângulos, dentre outros. Essa constatação compactua com as ideias fundamentais do ensino de matemática, contidas na Base Nacional Comum Curricular (BNCC):
devem ser enfatizadas também as tarefas que analisam e produzem transformações e ampliações/reduções de figuras geométricas planas, identificando seus elementos variantes e invariantes, de modo a desenvolver os conceitos de congruência e semelhança. Esses conceitos devem ter destaque nessa fase do Ensino Fundamental, de modo que os alunos sejam capazes de reconhecer as condições necessárias e suficientes para obter triângulos congruentes ou semelhantes e que saibam aplicar esse conhecimento para realizar demonstrações simples, contribuindo para a formação de um tipo de raciocínio importante para a Matemática, o raciocínio hipotético-dedutivo (BRASIL, 2018, p. 270).
Ao observar os objetos de conhecimentos e as habilidades propostas na BNCC (BRASIL, 2018, p. 278-317), é possível a concretização de alguns desses elementos matemáticos com mais clareza. No quadro 2, percebemos as relações dos conteúdos matemáticos emergentes do uso báculo com as diretrizes curriculares, estritamente no eixo temático de geometria.
Habilidades da BNCC relacionadas com a aplicação da medição de profundidade.
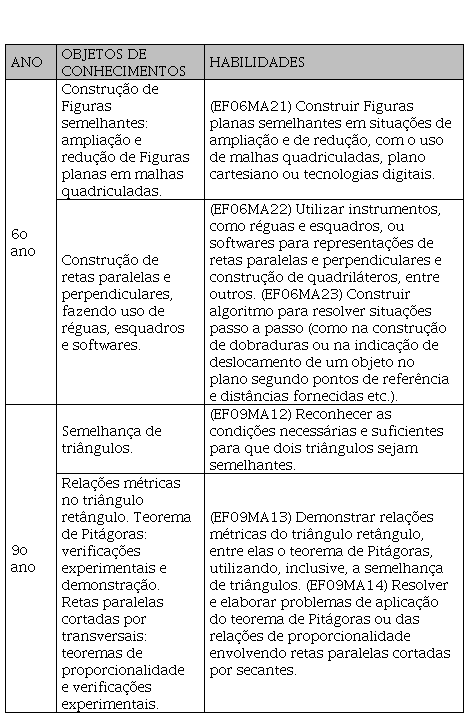
Fonte: Adaptado de Brasil (2018, p. 300-317).
Embora os anos finais do ensino fundamental não apresentem, diretamente, o cálculo de proporção, ele é muito usado para o estudo da semelhança de triângulos, que permeia todo o processo de aplicação do báculo para a situação escolhida neste estudo. Isso pode ser notado nas relações das grandezas diretamente e grandezas inversamente proporcionais, na utilização da regra de três produzida pelas semelhanças de triângulos, que são estudadas no 9o ano, enfatizando que grandezas, como as partes do báculo e as distâncias (comprimento e altura), são diretamente proporcionais.
Ao idealizar a interface entre o ensino e a história da matemática, vemos a possibilidade de aproximar os dois campos de conhecimento, sendo que eles possuem objetos de estudo bem definidos. Dessa forma, vislumbra-se o instrumento matemático como um importante elemento atrelado à interface, uma vez que ele incorpora conceitos matemáticos da antiguidade, fazendo-nos entender como o conhecimento era descrito em uma determinada época e como podemos usá-lo em uma perspectiva didática.
Ao estudar a situação de medição no tratado de Ramus (1636), observa-se que a utilização de seu báculo elenca várias situações cotidianas, como medir a altura de uma torre, a distância entre dois objetos distantes, bem como a profundidade do poço. Com tudo o que foi exposto, a situação tem uma gama de recursos a serem explorados, desde o início do enunciado até o final da explicação.
Apesar da situação de medição de profundidade requerer noções elementares da matemática, as ações de abstração chegam a ser dificultosas, uma vez que é preciso entender “a matemática” da época, juntamente com o contexto, para que o entendimento seja claro. Assim, o acesso ao processo de medição e os cálculos envolvidos mobilizam conhecimentos matemáticos incorporados no báculo, fazendo-nos ter uma visão complemente diferente do que temos hoje.
Nesse sentido, considera-se que é necessário fazer uma aplicação do báculo em uma situação real que envolva a medição de profundidade na formação de professores, visando compreender não só os saberes matemáticos incorporados na utilização, mas também elencar possíveis potencialidades didáticas na interface entre história e ensino de matemática.
https://www.revistasbemsp.com.br/index.php/REMat-SP/article/view/371 (pdf)
Síntese do conteúdo do capítulo nono de Via regia ad geometriam (1636).

Fonte: Elaborado pelos autores.

Figura 1
Partes do Báculo de Petrus Ramus
Elaborada pelos autores

Figura 2
Esquema matemático da situação de medição de profundidade.
Imagem adaptada de Ramus (1636, p. 125).

Figura 3
Esquema matemático das marcações no poço.
Elaborada pelos autores.

Figura 4
Esquema matemático na formação de triângulos.
Elaborada pelos autores.

Figura 5
Esquema de segmentos.
Elaborada pelos autores.
Habilidades da BNCC relacionadas com a aplicação da medição de profundidade.

Fonte: Adaptado de Brasil (2018, p. 300-317).


