



Seção Temática: Resolução de Problemas na Educação Matemática
Resolução de problemas contextualizados: análise de uma ação didática para o ensino de matemática nos anos iniciais do ensino fundamental
Solving contextualized mathematics problems: analysis of a didactic action for the teaching of mathematics in the early years of elementary school
Resolución de problemas contextualizados: análisis de una acción docente para la enseñanza de las matemáticas en los prim
Revista de Educação Matemática
Sociedade Brasileira de Educação Matemática, Brasil
ISSN: 2526-9062
ISSN-e: 1676-8868
Periodicidade: Cuatrimestral
vol. 17, núm. 1, 2020
Recepção: 09 Julho 2019
Aprovação: 16 Fevereiro 2020
Publicado: 01 Maio 2020

Resumo: O presente artigo[3] advém de uma pesquisa qualitativa de natureza interpretativa e teve entre seus objetivos investigar como problemas matemáticos contextualizados possibilitam a construção de estratégias de resolução a partir da interpretação e compreensão de seus enunciados. A pesquisa foi desenvolvida em duas turmas do 4º ano do Ensino Fundamental de uma escola pública do município de Curitiba (PR). O contexto foi criado a partir de sugestões dos alunos por meio de levantamento de interesse, que após sistematizados resultaram em um tema coletivo para as duas turmas. Problemas contextualizados foram criados em episódios encadeados, que foram resolvidos pelos alunos em seis encontros, sendo alguns em grupo e outros individualmente. Os processos de resoluções foram registrados por escrito e os diálogos gravados em áudio e vídeo. Concomitante a análise das resoluções, alunos foram entrevistados para esmiuçar estratégias resolutivas por eles elaboradas. Os resultados evidenciaram que o uso de temas de interesse dos alunos como base para a contextualização de problemas matemáticos contribuiu para o desenvolvimento de uma postura investigativa dos alunos, favoreceu a interpretação dos enunciados dos problemas possibilitando a percepção de relações matemáticas neles envolvidas e contribuiu para a aprendizagem conceitual dos conteúdos matemáticos curriculares.
Palavras-chave: Resolução de problemas, Problemas matemáticos contextualizados, Prática didática, Contexto.
Abstract: This article reports a qualitative research of an interpretive nature and had among its objectives to investigate how contextualized mathematical problems make possible the construction of strategies of resolution based on the interpretation and comprehension of its statements. The research was developed in two classes of the 4th year of elementary school in a public school in the city of Curitiba (PR). The context was created from suggestions of the students through a survey of interest, which after systematized resulted in a collective theme for the two classes. Contextualized problems were created in threaded episodes, which were solved by the students in six encounters, some in group and others individually. The solutions were recorded in writing and dialogues recorded in audio and video. Concomitant with the analysis of the resolutions, students were interviewed to analyze strategies that they worked out. The results showed that the use of topics of interest to the students as a basis for the contextualization of mathematical problems contributed to the development of an investigative posture of the students, favored the interpretation of the statements of the problems allowing the perception of mathematical relations in them involved and contributed to the conceptual learning of curricular mathematical contents.
Keywords: Problem-solving, Contextualised problem-solving, Didactic practice, Context.
Resumen: El presente artículo proviene de una investigación cualitativa de naturaleza interpretativa y tuvo como objetivo investigar cómo problemas matemáticos contextualizados posibilitan la elaboración de estrategias resolutivas a partir de la interpretación y comprensión de sus enunciados. La investigación se ha desarrollado en dos grupos de alumnos de cuarto grado de la Enseñanza Básica de una escuela pública del municipio de Curitiba (PR). El contexto se creó a partir de sugerencias de alumnos que después de sistematizados resultaron en un tema colectiva para los dos grupos. Los problemas contextualizados se crearon en episodios encadenados, que se han resuelto por los alumnos en el transcurso de seis encuentros, siendo algunos en grupo y otros individualmente. Los procesos de resolución realizados por los alumnos se registraron por escrito y los diálogos se grabaron en audio y vídeo. Concurrente al análisis de las resoluciones, los estudiantes fueron entrevistados con el fin de comprender mejor las estrategias resolutivas que ellos elaboraron. Los resultados evidenciaron que el uso de temas de interés de los alumnos como base para la contextualización de problemas matemáticos contribuyó al desarrollo de una postura investigativa de los alumnos, además de favorecer la interpretación de los enunciados de los problemas posibilitando la percepción de relaciones matemáticas involucradas y contribuir a la aprendizaje conceptual de los contenidos matemáticos curriculares.
Palabras clave: Resolución de problemas, Problemas matemáticos contextualizados, Práctica didáctica, Contexto.
Introdução
O ensino de Matemática por meio da resolução de problemas é defendido por inúmeros pesquisadores como uma metodologia que favorece a compreensão de conceitos matemáticos pelo aluno. Isto porque, de acordo com estudiosos, a interpretação e compreensão de um problema favorece a elaboração de estratégias próprias de resolução e a busca por validações dos resultados obtidos, desenvolvendo assim o pensamento autônomo (POLYA, 2006; SHOENFELD, 1996).
Consideramos importante ressaltar que assumir a resolução de problemas como metodologia de ensino não consiste em trabalhar problema matemático como um exercício para mecanização e fixação de conteúdo, mas sim como um ponto de partida para a aprendizagem de Matemática. Nesta perspectiva, o problema matemático é uma atividade que permite a mobilização, pelo aluno, de conhecimentos anteriores para, então, elaborar estratégias resolutivas próprias na busca de uma solução para o problema.
Compartilhamos do entendimento de Allevato e Onuchic (2014) de que práticas pedagógicas precisam posicionar o aluno como protagonista no processo de construção do conhecimento, oferecendo a ele oportunidade de desenvolver sua criatividade, autonomia e pensamento crítico e visualizamos no ensino por meio da resolução de problemas um caminho fecundo para tanto. Contudo, nos inquietamos diante da distância, muitas vezes, existente entre conteúdos matemáticos escolares e questões do cotidiano significativas para o aluno.
Nesse sentido, estamos atentas para o apontamento de Guérios e Medeiros Junior (2016, p. 226) sobre a contradição, não raras vezes existente, entre a intencionalidade didática de professores e a prática que desenvolvem. Dizem os autores que
O que, de fato, é uma contradição, é o professor primar por problemas que ensinem ao aluno o pensar autônomo, mas, na prática, priorizem exercícios de aplicação direta de algoritmos. Professores e alunos têm compreensões diferentes sobre contextos de enunciados havendo inquietação no processo de resolução devido à falta de valorização e entendimento da situação envolvida. Em geral, a não compreensão dos enunciados impede a identificação do contexto pretendido. (GUÉRIOS; MEDEIROS JUNIOR, 2016, p. 226)
Em vista disso, e com o propósito de ampliar as discussões acerca da resolução de problemas, ponderamos sobre a natureza dos enunciados de problemas matemáticos e, neste artigo, nos propusemos a investigar como problemas matemáticos contextualizados possibilitam a construção de estratégias de resolução a partir da interpretação e compreensão de seus enunciados.
O ensino de Matemática por meio de Resolução de Problemas
Estudos que versam sobre resolução de problemas não são recentes. George Polya, um dos pioneiros desta abordagem como metodologia de ensino, já apresentava em sua obra “How to solve it[4]” estratégias que orientam os alunos no processo de resolução de problemas. Tal literatura conquista leitores até os dias de hoje, sendo referência para muitas pesquisas.
Foi a partir da década de 1980 que a metodologia da resolução de problemas para o ensino de Matemática ganhou maior evidência no cenário mundial, com as publicações dos documentos An Agenda for Action e Standards 2000 pelo National Council of Teachers Matemathics [NCTM] que assinalam a importância da resolução de problemas. Tais documentos ecoaram também no Brasil, sendo referência para a elaboração dos Parâmetros Curriculares Nacionais [PCN] de Matemática (BRASIL, 1997; 1998) no final da década de 1990 que, por sua vez, entendem a resolução de problemas como um eixo do processo de ensino-aprendizagem de Matemática, um propulsor para a construção de conhecimento pelo aluno, posicionando-o no centro do processo educativo.
Este entendimento acerca da resolução de problemas exprime a ânsia de superar um ensino voltado para a memorização mecânica de conceitos matemáticos e técnicas operatórias. Ao contrário, valoriza a compreensão de conceitos pelo aluno e o desenvolvimento do seu pensamento autônomo e criativo.
Tal intencionalidade é reforçada na Base Nacional Comum Curricular [BNCC] (BRASIL, 2017), ao defender que a educação deve propiciar ao aluno o desenvolvimento de competências que favoreçam a aprendizagem. Explicitamos que “na BNCC, competência é definida como a mobilização de conhecimentos (conceitos e procedimentos), habilidades (práticas, cognitivas e socioeconômicas), atitudes e valores para resolver demandas complexas da vida cotidiana, do pleno exercício da cidadania e do mundo do trabalho”. (BRASIL, 2017, p. 8). Nessa direção, o ensino de Matemática deve possibilitar que o aluno compreenda conceitos, aproprie-se deles e mobilize-os na busca de soluções para situações diversas, não apenas no âmbito escolar, mas também as que emergem em sua cotidianidade.
Em nosso entendimento, o ensino de Matemática por meio da resolução de problemas, potencialmente, oferece subsídios para assegurar a premissa acima. Entretanto, ainda há uma percepção equivocada no que concerne a abordagem de resolução de problemas em sala de aula. Consideramos, então, válido pontuar algumas diferenças entre problema matemático e exercício matemático.
Para Echeverría e Pozo (1994) a principal diferença entre exercício e problema é que diante do primeiro o aluno possui em sua memória procedimentos, aprendidos por meio de rotinas automatizadas, que lhe permitem resolver o exercício rapidamente. Já diante de um problema, o aluno precisa elaborar estratégias resolutivas próprias, a partir da compreensão e organização dos dados apresentados.
Onuchic (1999) amplia essa discussão e entende que problema matemático não é um exercício de fixação que conduz o aluno ao treino de técnicas operatórias e à aplicação mecânica de conhecimentos anteriormente “aprendidos”, mas sim, uma atividade que tem o potencial de promover a aprendizagem na medida em que auxilia o aluno na compreensão e apropriação de conceitos matemáticos a partir das relações que estabelece entre eles no decorrer do processo de resolução de problemas. Para a autora, “[...] problema é tudo aquilo que não se sabe fazer, mas que está interessado em resolver”. (ONUCHIC, 1999, p. 215).
Em consonância a esse entendimento, Allevato (2005, p. 41) defende que “[...] uma questão será um problema se o aluno ainda não conhece os meios necessários à resolução, mas está interessado em resolvê-la”.
Para Guérios e Medeiros Junior (2016, p. 218) configuram-se como problema situações manifestas em enunciados “em que o aluno conjecture, elabore estratégias e descubra (heuristicamente) a solução do problema”. Ainda, em que “o aluno independe de tantas interferências para a promoção de sua aprendizagem, pois consegue caminhar por si na construção do conhecimento e na busca de soluções”.
Nessa direção, entendemos problema matemático como uma situação desafiadora para a qual o aluno não possui em sua memória um modelo de resolução. Por conseguinte, este precisa interpretar e compreender o enunciado do problema, mobilizar conhecimentos anteriores e elaborar estratégias resolutivas próprias, na busca de uma solução que apresente sentido matemático para a pergunta do problema.
A compreensão do enunciado do problema é um fator fundamental na atividade dos alunos, conforme a constatação de Guérios e Ligeski (2013, p. 3273) que ao investigarem relações entre compreensão textual e resolução de problemas em matemática por alunos do Ensino Fundamental, identificaram que “dificuldade na leitura comprometeu a compreensão textual dos enunciados, o que impossibilitou ao aluno vislumbrar uma estratégia de resolução para a situação configurada, por ele não compreendida”. Assim como para as autoras, este aspecto nos é importante, para que práticas pedagógicas possibilitem ao aluno desenvolver criatividade, autonomia e pensamento crítico, conforme nos acenou Allevato e Onuchic (2014), visto que estão associadas à compreensão sobre a circunstância em que o pensamento ocorre.
Pensando a resolução de problemas como processo, Polya (2006, p. 4-5) propõe um método organizado em quatro etapas de trabalho que são “compreender o problema, estabelecer um plano de resolução, executá-lo e fazer um retrospecto da resolução”. Vale ressaltar que não entendemos o método descrito por Polya (2006) como um roteiro a ser seguido passo a passo, mas sim como orientações que podem ocorrer de modo não linear, com o propósito de auxiliar o aluno no desenvolvimento do seu pensamento autônomo e criativo na medida em que reflete sobre problemas matemáticos e busca por soluções.
Ante o exposto, defendemos que o ensino de Matemática por meio da resolução de problemas auxilia o aluno no processo de construção do conhecimento e ressaltamos a necessidade, sem que isso signifique obrigatoriedade, de aproximar conteúdos matemáticos escolares às vivências do aluno, por concordar com o expresso na BNCC (BRASIL, 2017) sobre a importância de relacionar a Matemática a acontecimentos cotidianos.
Metodologia
A pesquisa qualitativa de natureza interpretativa que originou este artigo teve entre seus objetivos, o de investigar como problemas matemáticos contextualizados possibilitam a construção de estratégias de resolução a partir da interpretação e compreensão de seus enunciados. Foi desenvolvida em duas turmas do 4º ano do Ensino Fundamental de uma escola pública do município de Curitiba (PR). O contexto foi criado a partir de sugestões dos alunos por meio de levantamento de interesse. As sugestões foram sistematizadas e resultaram em um tema coletivo para as duas turmas. Problemas encadeados foram criados tendo como contexto o tema coletivo e foram resolvidos pelos alunos em seis encontros, sendo alguns em grupo e outros individualmente. As soluções foram registradas por escrito e os diálogos gravados em áudio e vídeo. Concomitante a análise das resoluções, alunos foram entrevistados para esmiuçar estratégias resolutivas por eles elaboradas.
Problemas matemáticos contextualizados: uma possibilidade didática
Atrai-nos a ideia de estabelecer relações entre conteúdos matemáticos escolares e a realidade dos alunos com o intuito de viabilizar a compreensão e apreensão de conhecimentos matemáticos por eles, e ponderamos sobre uma possibilidade, entre outras possíveis, de efetivar tal premissa, fazendo uso da metodologia de resolução de problemas em uma perspectiva de contexto.
Segundo Tufano (2002, p. 41) “Contextualizando tentamos colocar algo em sintonia com o tempo e com o mundo, construímos bases sólidas para poder dissertar livremente sobre algo, preparamos o solo para criar um ambiente favorável, amigável e acolhedor para a construção do conhecimento”.
Nessa direção, movidos pelo interesse de tornar aulas de Matemática mais atrativas e que instiguem o aluno a pensar matematicamente, nos propusemos, neste artigo, a investigar como problemas matemáticos contextualizados possibilitam a construção de estratégias de resolução a partir da interpretação e compreensão de seus enunciados. Para tanto, buscamos em Skovsmose (2000), Valero (2002), Giardinetto (1999) e Guérios, Gosmatti, Fernandes, Bagatin e Perine (2009) orientações para definirmos sobre referências cotidianas que podemos tomar como base para a escolha de um tema a ser utilizado como contexto dos problemas matemáticos.
Valero (2002), ao discorrer sobre contexto situacional e contexto sociopolítico, e Skovsmose (2000), ao abordar referências à semi-realidade e à realidade, defendem a importância do estabelecimento de relações entre conteúdos matemáticos escolares e a realidade do aluno. Percebemos nos documentos oficiais PCN (BRASIL, 1997; 1998) e BNCC (BRASIL, 2017) pensamento aproximado. Em vista disso, julgamos importante ponderarmos sobre o termo realidade.
Giardinetto (1999) defende a existência de uma realidade humanizada construída pelo indivíduo a partir de sua interpretação para a realidade natural, tendo como base as relações que estabelece com o meio e com os outros. Para o autor, neste movimento o indivíduo constrói um conjunto de saberes com o intuito de suprir suas necessidades e interesses. Desse modo, afirma que a realidade é um produto da construção humana e, por conseguinte, está sujeita a múltiplas interpretações segundo o olhar de quem a interpreta que, por sua vez, traz consigo saberes, crenças e valores aprendidos em suas relações sociais.
Entendimento similar observamos em Guérios, et al (2009) ao afirmarem que um mesmo fato de uma determinada realidade tomada como base para a ação didática não tem o mesmo entendimento por todos ao mesmo tempo, uma vez que é compreendido de modo diferenciado por cada um, em função da situação vivencial de cada um. Assim, compreendemos que em uma sala de aula nos deparamos não apenas com diferentes realidades, considerando fatores históricos-sociais que permeiam à vida de cada aluno, mas também com diferentes interpretações do real, alicerçadas em conhecimentos e convenções culturais aprendidos nas relações cotidianas.
Tal diversidade reflete, consequentemente, em variedade de interesses. Assim, o que pode ser um contexto significativo para um aluno, pode não ser para outro (GUÉRIOS et al, 2009). Em vista disso, optamos por investigar temas de interesses dos alunos, o que será descrito na próxima seção deste artigo, para conhecer o que, de fato, do cotidiano deles desperta interesse e pode mobilizá-los para a aprendizagem.
É importante esclarecer que defendemos a incorporação do cotidiano na organização da ação docente, com o cuidado de que tal incorporação não ocorra alheia às possibilidades de compreensão, pelos alunos, dos fatos que o compõem. Aliás, Giardinetto (1999, p. 58) fez este alerta ao afirmar que ocorre “em algumas pesquisas uma polarização entre “saber cotidiano” e “saber escolar”, enfatizando-se de forma unilateral a utilização do saber cotidiano, e, gerando com isso o fenômeno da supervalorização do saber cotidiano em detrimento de sua relação com o saber escolar”.
A construção dos problemas matemáticos contextualizados
Reiteramos que os problemas matemáticos contextualizados desta pesquisa foram inspirados no seriado Detetives do Prédio Azul[5] (D.P.A.) que, por sua vez, tem como eixo norteador um mistério a ser desvendado. Os três detetives, Sol, Bento e Pippo, são crianças que assumem a responsabilidade de resolver os mistérios que surgem na trama, e o fazem com êxito. Percebemos, no decorrer da entrevista, que este empoderamento das crianças [detetives] chamava a atenção dos alunos.
Nossa intencionalidade ao elaborar os enunciados dos problemas era despertar o interesse dos alunos e envolvê-los no contexto. Por isso, criamos mistérios que, para serem resolvidos, necessitavam de planejamento e desenvolvimento de estratégias matemáticas.
Também preservamos características e falas dos personagens da trama. Observamos, no seriado, que diante de um novo mistério os três detetives repetiam o bordão: Isso é mais um trabalho para... Os imbatíveis... Os invencíveis... Os xxxx... Detetives do Prédio Azul! A palavra, representada neste artigo por xxxx, alterava-se em cada episódio, adequando-se ao mistério em questão.
Os problemas matemáticos contextualizados foram denominamos de episódios, para aproximarmos da linguagem utilizada em seriados. Neste artigo, apresentamos um dos problemas do episódio II da primeira temporada (quadro 1). Selecionamos este episódio por permitir a observação do envolvimento dos alunos com o contexto criado, o movimento cognitivo de construção de diferentes estratégias resolutivas na busca de uma solução para o problema e o momento em que os alunos buscam pela validação da solução obtida, próprio da etapa denominada por retrospecto por Polya (2006).
Este problema teve como inspiração o episódio do seriado denominado “D.P.A. – Sumiços do Prédio Azul: Sumiço do lanche”[6]. Os problemas propostos constituíam uma sequência de situações. Desse modo, o “episódio II: O sumiço do lanche” faz menção, no início do enunciado, ao episódio apresentado aos alunos anteriormente [Agora, com todos os detetives de pés calçados, dá para aproveitar o resto da manhã]. Julgamos importante esclarecer que o episódio I abordava o sumiço dos sapatos dos detetives, que haviam sido “confiscados” por dona Leocádia [personagem da trama] e guardados em um cofre. Cabia, então, aos alunos descobrir a senha secreta deste cofre, composta por figuras geométricas planas, para recuperar os sapatos e devolvê-los aos detetives.
Na sequência apresentamos nossa análise tendo como base os dados coletados referentes à implementação do episódio II: O sumiço do lanche.
Resolvendo os mistérios com os D.P.A.: análise de dados
O encaminhamento didático utilizado para a implementação dos problemas matemáticos contextualizados desta pesquisa aproxima-se da proposta de Allevato e Onuchic (2014). No primeiro momento, os alunos realizaram a leitura individual e silenciosa do enunciado. Assim, tiveram a oportunidade de “[...] colocar-se em contato com a linguagem matemática e desenvolver sua própria compreensão do problema proposto.” (ALLEVATO; ONUCHIC, 2014, p. 45). Depois, um aluno fazia a leitura do problema em voz alta. É interessante relatar que após um aluno ler o enunciado, todos liam, em coro e entusiasmados, o bordão “Isso é mais um trabalho para... Os imbatíveis... os invencíveis... os raciocinadores... Detetives do Prédio Azul!”
Na sequência, discutiu-se sobre o enunciado do problema, buscando levantar questões por meio de interpretação de texto acerca do mistério a ser solucionado, realizando debate e reflexão sobre diferentes modos de pensar matematicamente na busca de uma solução. Para Allevato e Onuchic (2014) este momento é importante porque possibilita a troca de ideias entre os alunos, permite o desenvolvimento da oralidade e o aprimoramento da expressão e argumentação matemática.
O problema trazido para a análise, “episódio II: O sumiço do lanche”, foi realizado pelos alunos organizados em grupos, sendo seis no período da manhã, os quais denominamos de A, B, C, D, E e F, e seis grupos no período da tarde, denominados de G, H, I, J, K e L. Os nomes dos alunos são fictícios.
Reiteramos que no primeiro momento foi realizada a leitura do episódio II. Segundo Polya (2006) é importante que o aluno compreenda o problema e identifique a incógnita [o que precisa ser respondido], os dados [informações necessárias para a elaboração das estratégias resolutivas] e a condicionante [a relação existente entre os dados e a incógnita].
No momento em que os alunos identificavam as incógnitas do contexto do problema (descobrir em qual andar estava Theobaldo[7] antes de entrar no elevador e se foi ele quem pegou o sanduíche do Pippo), André disse: “Não sabemos. Precisamos seguir as pistas e fazer uma investigação”. Acerca desta fala, pontuamos algumas considerações (Quadro 2):

Em nosso entendimento, André demonstra envolvimento com o contexto criado e posiciona-se como um detetive frente a um mistério, assumindo a responsabilidade pela resolução do problema e, consequentemente, pela construção do conhecimento matemático.
Consideramos que o episódio II caracterizou-se como um problema matemático, pois os alunos estavam interessados em elaborar estratégias na busca de uma solução. Assim, retomamos as palavras de Onuchic (1999, p. 215) de que: “[...] problema é tudo aquilo que não se sabe fazer, mas que se está interessado em resolver”. Tivemos o cuidado de que o problema não apresentasse palavras-chave que induzissem a realização de determinados cálculos pelos alunos, mas sim uma situação matemática instigante, que desencadeasse a elaboração, por eles, de estratégias resolutivas de maneira autônoma.
Após leitura e discussão coletiva do episódio II, os alunos reuniram-se em grupo e dedicaram-se na busca de uma solução para o problema. Alguns julgaram necessário reler o episódio para melhor compreensão, como mostra o trecho do diálogo estabelecido pelo grupo D:
André: Agora eu vou ler de novo para entender melhor, tá?
[O aluno realizou a leitura do episódio II na íntegra].
Juliane: Mas a gente vai ter que reler só a parte do Theobaldo, do elevador.
[Juliane fez a releitura, pausada, do trecho que apresentava a movimentação de Theobaldo no elevador].
Em nosso entender, a releitura do episódio, ora na íntegra, ora de determinados fragmentos, revela uma postura de compromisso e de responsabilidade dos alunos com o processo de aprendizagem e de construção do conhecimento matemático.
Para Polya (2006), a busca pela compreensão do enunciado é a primeira etapa de trabalho no que tange a resolução de problemas. O autor defende que “O aluno precisa compreender o problema, mas não só isto: deve também desejar resolvê-lo”. (POLYA, 2006, p. 5). Para tanto, é importante que o enunciado seja atrativo para os alunos, além de, segundo Polya (1962), estar relacionado à suas experiências diárias.
Na sequência, Juliane propôs a leitura do trecho que apresentava a movimentação de Theobaldo. Assim, a aluna direcionou a atenção do grupo para os dados do problema, por perceber que essas informações dariam suporte para a elaboração da estratégia de resolução.
Compreendida a incógnita do problema e identificado os dados, o grupo D iniciou a elaboração de estratégias resolutivas, que corresponde a etapa de estabelecimento de um plano, segundo Polya (2006).
André foi o primeiro a formular uma hipótese:
André: Pelo o que eu entendi ele estava no primeiro andar, daí desceu um andar, foi pro térreo, subiu mais dois, foi pro segundo andar, daí desceu... Chegou no térreo. Ele estava no primeiro andar.
O grupo buscou pela validação da solução obtida e, na sequência, a apresentou para a professora[8]. Esta, ao perceber o equívoco cometido, questionou o grupo, desencadeando o seguinte diálogo:
Professora: Então agora confirmem se saindo do primeiro andar e fazendo toda essa caminhada ele [o Theobaldo] chega ao térreo.
André: Sim, porque ele estava no primeiro andar, desceu um foi pro térreo, subiu dois foi pro segundo andar.
Juliane: Depois desceu três.
Professora: Se estiver no segundo andar e descer três chega ao térreo?
Juliane: Não.
André: Vamos refazer.
Allevato e Onuchic (2014) orientam que no decorrer do trabalho com resolução de problemas o professor deve assumir uma postura de mediador do processo de aprendizagem. Tendo essa premissa em mente, buscamos questionar os alunos de modo que os incentivassem a realizar a conferência da resposta obtida.
Tal questionamento conduziu os alunos a uma reflexão acerca do caminho percorrido na busca por uma solução. Este momento é definido por Polya (2006) como retrospecto, a quarta etapa do processo de resolução de problemas. Vale ressaltar que ao perceber que a solução obtida apresentava erro, os alunos, prontamente, descartaram a possibilidade de Theobaldo estar no primeiro andar antes de entrar no elevador e formularam uma nova hipótese:
Gabriel: Ele estava no segundo andar, então... Deixa eu explicar. Ele estava no segundo andar, desceu um, ficou um, subiu dois, ficou três, desceu três... Onde é que ele foi parar? Então ele estava no segundo andar.
André: Se estivesse no segundo andar, desceu um, foi pro primeiro. Subiu dois, foi pro terceiro. Desceu três foi pro térreo.
Gabriel: O que eu falei?
André: Então faz a conta e faz a resposta.
Desta vez foi Gabriel quem apresentou uma nova resolução. Após a exposição da nova hipótese, André reformulou a fala do colega, com o intuito de realizar a conferência. Em nosso entendimento, os alunos posicionaram-se como protagonista do processo de aprendizagem, pois diante da percepção do erro não solicitaram à professora uma orientação [explicação], mas sim formularam nova hipótese, sem descartar o raciocínio desenvolvido.
Segundo Polya (2006), o retrospecto, além de ser importante para a verificação da solução obtida, deve motivar o aluno a refletir sobre outros meios de chegar ao mesmo resultado. Observamos essa preocupação entre os alunos do grupo D, pois após a elaboração da estratégia resolutiva os alunos traduziram a estratégia verbalizada em uma linguagem matemática, como mostram os cálculos elaborados pelo grupo (Figura 1):

Em consonância com o diálogo estabelecido, o cálculo apresentado parte da hipótese de que Theobaldo estaria no segundo andar. Desceu um andar (2 – 1 = 1), chegou ao primeiro. Subiu dois andares (1 + 2 = 3), chegou ao terceiro. Por fim, desceu três andares (3 – 3 = 0) e chegou ao térreo. Assim, os alunos atribuíram significado às operações efetuadas, utilizando a subtração para calcular os andares do prédio que Theobaldo desceu e a adição para calcular os andares que ele subiu. Além disso, relacionaram o zero ao andar térreo.
Resolvida a primeira incógnita, os alunos direcionaram a atenção para a segunda, ou seja, se foi Theobaldo quem pegou o sanduíche do Pippo. Diante desta questão, Carolina disse: “A gente vai ter que entender a história para responder. Ler desde o começo até o fim”.
Percebemos que o contexto apresentado no enunciado foi considerado, em sua totalidade, pelo grupo. A fala da aluna revela a preocupação em entender a situação matemática propondo, para tanto, a releitura do problema.
Vale ressaltar que pesquisas revelam a existência de uma relação entre competência leitora do aluno e sua habilidade em resolver problemas matemáticos (HEREBIA, 2007; MORAIS, 2010; SILVA, 2011; GUÉRIOS; LIGESKI, 2013). Nessa direção, observamos que o trabalho com problemas matemáticos contextualizados envolvendo um tema de interesse dos alunos, auxilia no processo de compreensão do enunciado, visto a preocupação destes em interpretar a situação apresentada e elaborar estratégias resolutivas alicerçadas na compreensão do contexto do problema.
Observamos, novamente, o envolvimento dos alunos com o contexto do problema no seguinte trecho do diálogo:
Gabriel: Onde o sanduíche estava? Vai ter que ler tudo de novo.
(...)
Juliane: A gente sabe que o Theobaldo estava no segundo andar, mas onde é que estava o sanduíche?
André: O sanduíche estava no terceiro. Ele estava no segundo e o sanduíche no terceiro.
Juliane: Mas se ele usou magia?
[No seriado, Theobaldo é um mago!.
Gabriel: Mas é antes do percurso todo?
Juliane: Mas ele não é mentiroso. Ele não desceu do elevador.
Caroline: Ele não desceu do elevador. Ele saiu do segundo, o sanduíche estava no terceiro.
(...)
André: Não, ele não pegou o sanduíche. Porque ele estava brincando no elevador.
Com base no diálogo, observamos que eles ponderaram sobre o contexto do problema, e não se limitaram aos dados numéricos apresentados. Destacamos dois exemplos que ilustram nossa afirmativa. Primeiro, quando Juliane diz que Theobaldo não é mentiroso ela considera características do personagem do seriado, o que revela o estabelecimento de um diálogo com o contexto criado, no decorrer do processo de resolução do problema. Segundo, quando o aluno Gabriel questiona o que Theobaldo teria feito antes de entrar no elevador, demonstra o entendimento de que o problema está inserido em um contexto maior, ou seja, que o enunciado é um extrato de uma dada situação, mas que existem outros acontecimentos que não estão ali relatados.
Após a análise do problema e do debate acerca de diferentes possibilidades, o grupo concluiu que não foi Theobaldo quem pegou o sanduíche, uma vez que este estava no terceiro andar do prédio e aquele no segundo, sendo esta a solução por nós esperada.
Os grupos L e H também efetuaram cálculos para resolver o problema, utilizando a adição para calcular os andares que Theobaldo subiu e a subtração para calcular os andares que ele desceu. Já outros sete grupos utilizaram uma figura como estratégia resolutiva. No momento da entrevista, Janaína justificou esta escolha: “A gente fez um desenho pra representar o espaço, daí a gente foi ligando os andares.” Eis um exemplo de resolução no qual a figura é utilizada como estratégia resolutiva (Figura 2):
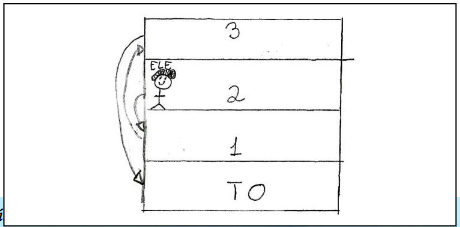
Na Figura 2 observamos que os alunos utilizaram flechas para representar a movimentação de Theobaldo ao subir e descer os andares do prédio. Pelas marcações de flechas apagadas, percebíveis na folha original de resolução, observamos que os alunos formularam outras hipóteses antes de chegar à solução final. Discussões em torno de diferentes hipóteses também foram evidenciadas no diálogo estabelecido pelo grupo C, como mostra o trecho que segue:
Paulo: Ele desceu um andar, foi pro térreo, aí subiu mais dois, chegou no segundo, daí ele desceu mais três, chegou no térreo e ficou.
Roberta: Sim, só que não foi do terceiro, foi do segundo pro térreo. Não tem como.
Paulo: É, não tem como ele sair do segundo e ir pro térreo de volta. Está confuso.
Professora: Em qual andar Theobaldo entrou no elevador?
Paulo: No primeiro.
Roberta: Ele estava no primeiro andar, daí desceu e foi pro térreo. Subiu mais dois, mas não tem o três. Mas como assim? Ele não subiu pro três?
Professora: Mas se essa hipótese não deu certo, será que ele estava no primeiro andar?
Roberta: Ele devia estar no terceiro.
Fábio: Como no terceiro? Ele não tem como subir dois.
Eduardo: Vamos fazer todos os andares.
Inicialmente, Paulo partiu da hipótese que Theobaldo estaria no primeiro andar antes de entrar no elevador. Roberta, ao refletir sobre a hipótese elaborada por Paulo com base em sua compreensão para o problema, percebeu o equívoco, pois estando Theobaldo no segundo andar não seria possível descer três andares e chegar ao térreo. Assim, Roberta percebeu que Theobaldo deveria estar, nesta etapa da resolução, no terceiro andar.
Roberta utiliza o raciocínio inverso como estratégia resolutiva, ou seja, busca refazer o caminho de Theobaldo partindo do fim para o início, pois entende que na última movimentação ele precisava estar no terceiro andar para, então, descer três andares e chegar ao térreo. Todavia, em nosso entendimento, a aluna ainda não domina o raciocínio inverso, posto a dificuldade que apresenta em expressar-se matematicamente para ser entendida pelos colegas, mas encontra-se em processo de construção deste conceito.
Na sequência do diálogo, Roberta indagou: “Mas como assim? Ele não subiu pro três?” Observamos que mesmo identificando que a hipótese apresentada por Paulo não era correta, Roberta não a descartava.
Como a verbalização da estratégia resolutiva não havia conduzido a uma solução satisfatória, Eduardo propôs representar a ideia matemática contida no problema por meio de uma figura, registrando os andares do prédio (Figura 3). É interessante observar a autonomia deste aluno ao propor o desenvolvimento de outra estratégia de resolução.

Diferente do grupo A, o grupo C não utilizou flechas para representar a movimentação de Theobaldo, mas utilizou a figura como ponto de apoio para o desenvolvimento das estratégias resolutivas. Nesse caso, a figura favorece a interpretação do problema pelo aluno, auxiliando a compreensão da ideia matemática nele vinculada. Na sequência do diálogo, Fábio elaborou uma nova hipótese:
Fábio: Olha... Ele estava no segundo andar. Desceu um, daí subiu dois, desceu três e foi pro térreo. É, foi pro térreo, não tem mais pra onde ele ir.
Paulo: Daí a pergunta dois. Será que foi ele que pegou o sanduíche do Pippo?
Eduardo: Não. Porque ele estava no segundo andar e o sanduíche estava no terceiro. Não foi ele que pegou.
(...)
Eduardo: Coloca assim: O Theoblado é inocente.
Após as discussões, o grupo chegou ao consenso de que Theobaldo estava no segundo andar antes de entrar no elevador. Na sequência, Paulo retomou a segunda incógnita do problema: “Será que foi ele que pegou o sanduíche do Pippo?” Eduardo, com base nos dados presentes no enunciado, considerou Theobaldo inocente, pois se o lanche estava no terceiro andar e Theobaldo no segundo, logo não poderia ser ele quem pegou o sanduíche do Pippo.
Houve ainda um grupo que desenvolveu a estratégia resolutiva apenas oralmente, não realizando registro em folha. Após discussões, os alunos apresentaram a seguinte solução: “Ele estava no 2º andar. Ele não é o culpado. Porque ele não saiu do elevador, só no térreo”. No diálogo estabelecido pelo grupo é interessante observar a satisfação após a resolução do problema:
Rodrigo: Só quando ele chegou no térreo que ele saiu do elevador, só no térreo. Então ele não é o culpado, porque o sanduíche estava no terceiro andar.
(...)
Aline: Ele não é o culpado.
Rodrigo: Gente, é isso. Ele não é o culpado.
Aline: Nós somos os D.P.A.
Rodrigo: Nós somos os imbatíveis, os invencíveis, os raciocinadores... Detetives do Prédio Azul.
O grupo G foi o único que se preocupou em identificar que conta precisaria ser feita para resolver o problema. A aluna Carla questionava com certa frequência qual era a conta que precisava ser feita. Em um determinado momento, o grupo decidiu somar os andares do prédio (3+2+1=6). Em nosso entendimento, a preocupação excessiva em estruturar um algoritmo para responder ao problema, sem antes compreendê-lo, constituiu um obstáculo para o grupo. Para nós, a ação de colocar em evidência informações numéricas para então efetuar um determinado cálculo, revela um hábito mecânico de alguns alunos, por acreditarem que um problema matemático precisa, necessariamente, de cálculo para ser resolvido.
Observamos que o resultado obtido com a soma (3+2+1=6) não foi utilizado como resposta ao problema pelo grupo G. No momento da entrevista, Carla explicou que desconsideraram este resultado “Porque só tinha três andares”. Assim, o grupo percebeu que o resultado obtido não apresentava sentido matemático para a pergunta do problema, mas não desenvolveram outra estratégia resolutiva. Por fim, “concluíram” que Theobaldo estaria no terceiro andar do prédio, mas não souberam explicar, no momento da entrevista, como chegaram a essa solução.
No entanto, vale ressaltar que o grupo G mudou a postura diante dos episódios apresentados na sequência, não se limitou a buscar por palavras-chave que indicassem uma “conta” a ser feita, mas procuraram compreender o contexto do problema para, então, compor estratégias próprias de resolução, ora utilizando cálculos, ora desenhos, ora esquemas que traduzissem o enunciado em uma linguagem matemática.
Considerações finais
No presente artigo investigamos como problemas matemáticos contextualizados possibilitam a construção de estratégias de resolução a partir da interpretação e compreensão de seus enunciados. Observamos que os alunos envolveram-se com o contexto criado, tiveram uma postura de detetives diante de um mistério a ser elucidado e assumiram a responsabilidade pela resolução dos problemas.
Durante as atividades, observamos um movimento cognitivo autônomo dos alunos no levantamento de suposições, na elaboração de estratégias de resolução, na análise dos dados do problema e na avaliação do resultado obtido, buscando verificar se a solução encontrada apresentava sentido matemático para a incógnita do problema.
No decorrer do processo de resolução, os alunos mobilizaram conhecimentos matemáticos anteriores e refletiram sobre como poderiam utilizá-los em prol da solução para o problema. Mobilizaram também conhecimentos não matemáticos, ou seja, o que sabiam sobre o tema utilizado como contexto. Desse modo, os alunos não dissociaram o contexto linguístico do problema e a situação matemática nele envolvida, considerando fatores que poderiam influenciar na resolução do problema, além dos dados numéricos.
Nessa direção, defendemos que trabalhar com problemas matemáticos em uma perspectiva de contexto que considere e valorize temas presentes nas relações cotidianas dos alunos reflete de maneira positiva na aprendizagem dos mesmos. Nossa premissa é fundamentada na observação da postura responsável, motivada e autônoma dos alunos diante dos problemas matemáticos contextualizados.
Referências
ALLEVATO, Norma Suely Alberto. Associando o computador a resolução de problemas fechados: análise de uma experiência. Rio Claro: Universidade Estadual Paulista, 2005. 370 p. (Tese).
ALLEVATO, Norma Suely Gomes Alberto; ONUCHIC, Lourdes De La Rosa. Ensino – Aprendizagem – Avaliação de Matemática: por que Através da Resolução de Problemas? In: ONUCHIC, Lourdes De La Rosa et al. Resolução de Problemas: Teoria e Prática. Jundiaí: Paco Editorial, 2014. p. 35-52.
BRASIL. Parâmetros Curriculares Nacionais: Matemática. Brasília: MEC/SEF, 1997.
BRASIL. Parâmetros Curriculares Nacionais: Matemática, 3º e 4º ciclos. Brasília, DF: MEC/SEF, 1998.
BRASIL. Base Nacional Comum Curricular. Brasília, DF: MEC, 2017.
ECHEVERRIA, María Del Puy Pérez. POZO, Juan Ignacio. Aprender a Resolver Problemas y Resolver Problemas para Aprender. In: POZO et al (Org) La solución de problemas. Madrid: Santillana, 1994.
GIARDINETTO, José Roberto. Matemática escolar e matemática da vida cotidiana. Campinas: Autores Associados, 1999.
GUERIOS, Ettiène; GOSMATTI, Anderson; FERNANDES, Andressa; ZARAMELA, Débora; PERINE, Glória Lucia. Estudo de elementos componentes da prática didática e metodológica de professores que ensinam matemática. Anais Encontro Paranaense de Educação Matemática, Guarapuava: SBEM Pr, 2009, p. 431-443.
GUÉRIOS, Ettiène; LIGESKI, Arivana Izabel Stanski. Resolução de Problema em matemática na Educação Básica: problema em matemática ou em linguagem? Actas VII CIBEM. Uruguay: SEMUR. 2013. p. 3266-3273. http://www.cibem7.semur.edu.uy/7/actas/pdfs/1230.pdf . Acesso em 25 de junho de 2019
GUERIOS, Ettiène.; MEDEIROS JUNIOR, Roberto José. Resolução de problemas de matemática no ensino fundamental: uma perspectiva didática. In: BRANDT, Celia Fink.; MORETTI, Méricles. Tadeu. (Orgs) Ensinar e aprender matemática: possibilidades para a prática educativa. Ponta Grossa: Editora UEPG, 2016, p. 209-231
HEREBIA, C. F. B. Leitura, interpretação e resolução de problemas matemáticos de estruturas aditivas. Campo Grande: Universidade Católica Dom Bosco, 2007. 183p. (Dissertação)
Morais, Maria das Dores de. Papel da Compreensão Leitora na Resolução de Problemas Matemáticos. Recife: Universidade Católica de Pernambuco, 2010. 103 p. (Dissertação).
MUNDO GLOOB. D.P.A. - Sumiços do Prédio Azul: Sumiço do lanche. . Acesso em 15 set. 2019.
ONUCHIC, Lourdes de la Rosa. Ensino-aprendizagem de matemática através da resolução de problemas. In: BICUDO, Maria Aparecida Viggiani. (Org.) Pesquisa em Educação Matemática: concepções e perspectivas. São Paulo: UNESP, 1999. p. 199-218.
POLYA, George. On Lerning, Teaching and Learning Teaching. In: Mathematical Discovery (1962) cap. XIV. . Acesso em: 28 junho 2019.
POLYA, George. A arte de resolver problemas: um novo aspecto do método matemático. Rio de Janeiro: Interciência, 2006.
SCHOENFELD, A. H. Por quê toda esta agitação acerca da resolução de problemas? In: ABRANTES, P.; LEAL, L. C.; PONTE, João Pedro. (Org) Investigar para aprender matemática. Lisboa: APM, 1996. p. 61-71.
SILVA, P. V. da. O aprendizado de regras matemáticas: uma pesquisa de inspiração wittgensteiniana com crianças da 4ª série no estudo da divisão. Belém: Universidade Federal do Pará, 2011. 101 p. (Dissertação).
SKOVSMOSE, Ole. O cenário de investigação. Bolema, n. 14, p. 66-91, 2000.
SOUTO, F.C.F. Contribuições do ensino da matemática por meio da resolução de problemas contextualizados nos anos iniciais do Ensino Fundamental. Curitiba: Universidade Federal do Paraná, 2018. 189 p. (Dissertação).
TUFANO, Wagner. Contextualização. In: FAZENDA, Ivani. Dicionário em construção: interdisciplinaridade. São Paulo: Cortez, 2002, p. 40-42.
VALERO, P. Consideraciones sobre el contexto y la educación matemática para la democracia. Quadrante, vol. 11, n.º 1, 2002.
Notas
Ligação alternative
https://www.revistasbemsp.com.br/REMat-SP/article/view/274/pdf (pdf)

