



The evolution of project portfolio selection methods: from incremental to radical innovation
The evolution of project portfolio selection methods: from incremental to radical innovation
Revista de Gestão, vol. 26, no. 3, 2019
Universidade de São Paulo
Abstract:
Abstract Purpose The purpose of this paper is to identify how project portfolio selection (PPS) methods have evolved and which approaches are more suitable for radical innovation projects. This paper addressed the following research question: how have the selection approaches evolved to better fit within radical innovation conditions? The current literature offers a number of selection approaches with different and, in some cases, conflicting nature. Therefore, there is a lack of understanding regarding when and how to use these approaches in order to select a specific type of innovation projects (from incremental to more radical ones). Design/methodology/approach Given the nature of the research question, the authors perform a systematic literature review method and analyze 48 portfolio selection approaches. The authors then classified and characterized these articles in order to identify techniques, tools, required data and types of examined projects, among other aspects. Findings The authors identify four key features related to the selection of radical innovation projects: dynamism, interdependency management, uncertainty treatment and required input data. Based on the content analysis, the authors identified that approaches based on different sources and nature of data are more appropriated for uncertain conditions, such as behavioral methods, information gap theory, real options and integrated approaches. Originality/value The research provides a comprehensive framework about PPS methods and how they have been evolving over time. This portfolio selection framework considers the particular aspects of incremental and radical innovation projects. The authors hope that the framework contributes to reinvigorating the literature on selection approaches for innovation projects.
Keywords: · Radical innovation · Portfolio management · Decision support · Project selection methods.
1. Introduction
There are two ways for a business to succeed at new products: doing projects right, and doing the right projects.
(Cooper, Edgett, & Kleinschmidt 2002)
Project portfolio selection (PPS) is an iterative process whereby managers select projects from available proposals and current projects, in order to meet organizational objectives (Archer & Ghasemzadeh, 1999). This process is crucial to maintain the competitive advantage, enabling the company to focus on the most relevant and strategic projects. However, firms struggle in managing this process. PPS’ complexity relies on two main facts. First, the information required to determine whether a project could be successful or not is extremely difficult – if not impossible – to know (Baker, 1974). And second, because the project and environment conditions are too volatile, strategic goals might change, promoting high levels of uncertainty (Rice, O’Connor, & Pierantozzi, 2008).
Different methods and approaches have been proposed to address the PPS (Bard, Balachandra, & Kaufmann, 1988; Cooper, 1993; Regan, Ben-Haim, Wilson, Lundberg, Andelman, & Burgman, 2005). Current literature offers a number of increasingly sophisticated project selection approaches, including multi-criteria decision methods, scoring-based and simulation techniques, among others (Zhang, Yang, Dou, & Jiang, 2016). However, the current literature presents an “interesting dichotomy”: although there are an increasing number of frameworks supporting PPS, the adoption by firms and its impact remains limited. In addition, there is a lack of theoretical foundations for these frameworks (Kavadias & Chao, 2008).
Other scholars have also identified similar problems in PPS literature (Beaujon, Marin, & McDonald, 2001; Cooper, Edgett, & Kleinschmidt, 1999; Kavadias & Chao, 2008). Indeed, years of research provided a fragmented and disperse knowledge on PPS, increasing the difficulty of convergence and accumulation of knowledge. To some extent, the existence of this fragmentation might also impact the adoption by firms. The development and adoption of PPS are more difficult for radical innovation, in which managers face high uncertainties in structuring and selecting projects. According to Brasil, Salerno and Gomes (2018), inappropriate selection methods might restrain radical innovation proposals, since, typically, the PPS process has been centered on the assessment of ex ante information, such as estimated costs, profits or market share, that only can be confirmed after launching the project (Zhang et al., 2016). In sum, there are two major concerns in PPS literature, which can render the consolidation of the field more difficult. First, there is a lack of a comprehensive framework regarding how the PPS approaches evolved. And second, there is a lack of understanding of how these different approaches might be associated with different degrees of innovation.
To reduce these two major gaps, the following research question drives our research:
RQ1.
How have the PPS approaches evolved to better fit within radical innovation?
Employing a systematic literature review, we aim to identify which approaches are more suitable for radical innovation projects and what aspects are crucial to manage radical innovation portfolios. Our goal is to go beyond the last review on PPS methods, dated from more than 10 years ago (Cooper et al., 1999), capitalizing on more recent works. Addressing this research question is fundamental to theory and practice. First, there is a lack of understanding regarding when and how to use these approaches to select the specific level (degree) of the innovation project (from incremental to more radical ones). Likewise, without a proper method, firms might not be able to select the opportunities related to radical innovations (Brasil, Salerno, & Gomes, 2018). Using a kind of method that fits all approaches, firms might fail in differentiating the valuation and selection of incremental and radical innovation. Finally, it is also important to determine whether newer PPS methods meet the particular features of radical innovation projects in order to provide a guide for future research.
This paper provides important insights that advance the knowledge on PPS literature. First, we show how PPS evolved. This is especially important to new scholars in the field, who might face difficulties in building a big picture of how this field is structured. Second, we identified the main characteristics of different PPS approaches. This finding provides a rich portrait regarding the approaches, helping scholars and practitioners to identify when and how to use these approaches according to the innovation level. Finally, we provide a theoretical framework in which we associate these approaches according to the innovation level.
This study is structured in five sections as follows. Section 2 presents the methodological procedures including the documents sample selection and the analysis of the methods. Section 3 discusses the PPS approaches, describing each of the 12 taxonomies identified. In Section 4, we discuss the key issues for radical innovation portfolio management and which approaches are more suitable to this end. In addition, we elaborated an integrated portfolio selection method for radical innovation framework, based on the main characteristics and advantages of the approaches. Finally, Section 5 is concluded with the final considerations and future research directions.
2. Methodology
To obtain an overview of the evolution of PPS, a systematic literature review was performed. This methodology enforces explicit methods to perform a thorough research and analysis, underlining how a determined field has evolved, and enabling the identification of consensus or divergence among studies and theories (Briner & Denyer, 2010).
2.1 Sample selection procedure
The collecting methods’ process started through the search on the Web of Science database, which provides different searching and browsing options to obtain higher accuracy during the research. We applied the keywords: “Project Portfolio Selection,” in order to gather the broadest number of related works. The search returned 175 documents; this sample was refined selecting only the pertinent predefined categories as follows: “management,” “operations research management,” “engineering industrial” and “business.” Additionally, we focused our research only on “article,” because this type of documents is peer-reviewed – an important indicator of quality. We then reached out 75 documents.
Another selecting parameter was the inclusion of articles whose purpose was the proposition or improvement of method or approach for PPS. We read again the titles, abstracts and keywords. Based on this process, 35 articles related to “Project Portfolio Selection” were obtained. Notwithstanding, four documents referenced by Cooper, Edgett, and Kleinschmidt (1999) were added and other works were included too because they are recurrently cited by the studies in our sample. In total, 48 articles were selected.
2.2 Methods analysis procedure
Once the sample of articles was established, the first stage was to read them identifying the relevant points and the main contributions including proposed frameworks, techniques, tools, examples of application and required data. Based on Cooper et al.’s (1999) portfolio selection methods classification, we defined 12 taxonomy categories to classify the PPS approaches. The categories are: financial, probabilistic, options pricing, strategic, scoring, combinatorial optimization, behavioral, mapping approaches, real options, integrated methods, information gap theory and scenario-based approach. Table I shows the number of documents per year and methods categories. Combinatorial optimization (15) and integrated methods (13) have the greatest number of approaches and also represent the categories more explored in the last 10 years (ten and five documents, respectively).
Afterward, we carefully examined each PPS approach. We then identified four key requirements that PPS methods must meet in order to address radical innovation projects: dynamism, interdependencies, uncertainties and required input data. Based on these analyses, we proposed an integrated portfolio selection method for radical innovation (Section 5).
3. Project portfolio selection methods
According to Cooper et al. (1999), portfolio selection methods have progressively changed since the first methods emerged in 1960. At that time, methods were strongly focused on mathematical techniques. Over time, because the business and technology environment became more complex, more sophisticated methods emerged. Scholars identified that some of these approaches consist of prescribed solutions (one fits all), which might not fit with the vast variety of project and firms’ conditions (Chien, 2002; Baker, 1974). Furthermore, these prescribed aggregate methods raise a paradigm wherein a given set of projects (usually competing for limited resources) must be appraised in order to choose the ones which will maximize profits. Although these methods might be useful for more incremental innovation, an increasing research stream suggested that prescribed methods are not sufficient to analyze radical innovation projects due to the large numbers of unpredictable variables and knowledge gaps (e.g. Baker, 1974; Archer & Ghasemzadeh, 1999; Ghapanchi, Tavana, Khakbaz, & Low, 2012). In the following sections, we present 12 methods for PPS.
3.1 Financial methods
In these methods, the most important selection criterion is profitability and the objective is to establish a portfolio that maximizes expected returns (Bard et al., 1988). This is one of the most widely adopted methods by managers for screening projects (Chien, 2002; Dutra, Ribeiro, & Carvalho, 2014), and basically, are utilized to assess projects individually. Two documents were identified within this category (Table II).
3.2 Probabilistic methods
Among the most popular probabilistic methods are Monte Carlo simulation and Bayesian theory. These methods analyze different scenarios producing distributions of possible outcome values. Some methods are stochastic, using random values. Archer and Ghasemzadeh (1999) indicate that simulation techniques are more effective to analyze risk (Table III).
3.3 Option pricing theory
Option pricing uses mathematical models to calculate how demand varies at different prices’ levels. These models work with three critical pricing elements: pricing strategy, both buyer and seller value of the product, and techniques and elements that affect profitability (Galai & Masulis, 1976). According to Chien (2002), mathematical models are slightly used by managers because these models tend to do not consider the diversity of projects and criteria (Table IV).
3.4 Strategic methods
Since selecting the right projects is extremely critical, not just to maintain the competitive position, but also to achieve financial goals (Cooper et al., 2002), authors have been exploring selection methods driven basically by strategic objectives. Zeynalzadeh and Ghajari (2011)raise particular awareness about the hierarchy of strategy (i.e. organization, portfolio and project strategy) to be considered during the process of project selection. Strategic Buckets is one of the most widespread methods, in which managers create budget buckets where projects are categorized and prioritized (Cooper et al., 2002). These methods involve both external and internal considerations of the firm (Archer & Ghasemzadeh, 1999), enabling a focused perspective from the entire context (Table V).
3.5 Scoring methods
Basically, projects are screened based on a set of different requirements and aspects. Projects are eliminated if they do not meet the requirements and selected if they meet most part of these requirements (Archer & Ghasemzadeh, 1999). Scoring methods are a quantified extension of a checklist and rely on subjective ratings of managers. This fact presents a weakness because such ratings and weights are arbitrarily determined (Cooper, 1981), and this is one of the reasons why scoring methods could work better with objective-centered approaches. This method is also popular in practice because of its simplicity of execution (Hall & Nauda, 1990) (Table VI).
3.6 Combinatorial optimization
This category includes methods such as multi-criteria decision-making methods (MCDM), data envelopment analysis and analytical hierarchy approaches (AHP). According to Razi and Shariat (2017), MCDM are based on the utility theory and assist the human constraints to deal with profits and loss. In AHP models, criteria and alternatives are arranged in hierarchical structures in at least three levels, in order to prioritize the criteria within each level (Amiri, 2010).
According to Archer and Ghasemzadeh (1999), these methods are complex and difficult to apply, and also require a lot of information. Another constraint stems from the use of Technique for Order of Preference by Similarity to Ideal Solution and crisp values which are not recommended for handling uncertainties since these techniques work with single numeric values (Amiri, 2010). However, robust and specialized assessing algorithms may be useful for early screening when there is a large number of potential projects (Beaujon et al., 2001; Abbassi, Ashrafi, & Tashnizi, 2013). The approach proposed by Amiri (2010)incorporates fuzzy numbers, enabling managers to introduce interval judgments improving handling uncertainty issues (Table VII).
3.7 Behavioral methods
These methods aim to create a consensus based on experts and managers’ opinions to decide which projects should be undertaken. For Cooper et al. (1999), this taxonomy is particularly useful during the initial stages of the project selection, in which, virtually, these opinions might be the single input data available (Table VIII).
3.8 Mapping approaches
In this taxonomy, projects are plotted against various parameters in form of matrices or bubble diagram in which it is possible to visualize the strategic position of the firm’s product (Archer & Ghasemzadeh, 1999). Mapping methods have gained wide popularity among companies. For instance, Linton, Walsh and Morabito (2002) mentioned firms, such as 3M, Lucent Technologies or Procter and Gamble, which have implemented such mapping method (Table IX).
3.9 Real options
These methods incorporate learning models to resolve uncertainties through the experience gained over time. Differently from traditional economic analysis (e.g. discounted cash flow), the real options model is a fluctuating investment decision and assumes that the strategy may evolve depending on the real characteristics of the environment (Mun, 2005). It also helps managers to define a portfolio (which projects and when they should be run) among several seemingly economic outcomes and projects. Brasil et al. (2018) mention some barriers to adopt real options in PPS by firms: mathematical complexity, non-intuitive outcomes, and difficulties to handle unknown uncertainties, among others (Table X).
3.10 Integrated methods
Integrated methods are those in which two or more different taxonomies are employed in order to guide the portfolio selection process (Table XI).
3.11 Information gap theory
This method assists the decision-making process in situations under several knowledge gaps. It works with a mathematical process model, performance requirement and uncertainty model (Regan et al., 2005). Through the information gap model, analysts can identify what they believe to be true and important regarding the system, enabling the evaluation of robustness (identifying possible bad outcomes) and opportunity (windfall chances).
Differently from traditional selection methods, which are based on maximum expected benefits, in this method, the focus is on the identification of knowledge gaps, uncertainties and risks, in order to determine the least vague portfolio (Table XII).
3.12 Scenario-based approach
One of the main concerns of this approach is to address exogenous uncertainties, which are defined by Liesiö and Salo (2012, p. 162) as missing data or information “which are not influenced by the projects” (e.g. macroeconomic developments or rate of industry growth). This approach proposes to deal with exogenous uncertainties through the scenarios technique. Scenario planning enables a company to imagine possible futures through exploring “the joint impact of various uncertainties” (Shoemaker, 1995, p. 26). For Shoemaker (1995, p. 27), scenarios “attempt to capture the richness and range of possibilities, stimulating decision makers to consider changes they would otherwise ignore.”
The methods rely on the assumption that, through mathematical models and functions, it is possible to complete the information provided by experts, to build a scenario and identify synergies and probabilities. Scenario-based methods require specific and sophisticated knowledge to operate, thus, its applicability and diffusion are restricted (Archer & Ghasemzadeh, 1999) (Table XIII).
4. Results and discussion
4.1 Portfolio selection for radical innovation projects
In this section, we develop a discussion by bridging incremental and radical innovation levels and PPS approaches. First, integrated methods (i.e. those that enable managers to employ different techniques and different input data) are more convenient to adopt in both cases – incremental and radical innovations (Archer & Ghasemzadeh, 1999; Cooper et al., 1999; Dutra et al., 2014). This is also especially relevant for radical innovation, since no single method has all the features required to respond adequately under uncertain circumstances. Coldrick, Longhurst, Ivey, and Hannis (2005) recognize that optimization methods are powerful, but if combined with scoring, behavioral or mapping methods, they would be more beneficial. Second, qualitative judgment is more appropriate to deal with radical innovation (Archer & Ghasemzadeh, 1999; Cooper, 1981; Fahrni & Spätig, 1990). For instance, mapping or scoring methods are very useful to identify which projects to cut-off regarding the number of uncertainties and risks. Quantitative methods seem to be more suitable for handling risk (Fahrni & Spätig, 1990), rather than uncertainty in which the probabilities are “unknowable” (Brasil et al., 2018). However, some techniques employed by quantitative methods might handle uncertainties, such as is the case of fuzzy theory (combinatorial optimization) or volatility metrics (real options) (Jafarzadeh, Akbari, & Abedin, 2018; Wang & Hwang, 2007).
Another important aspect to consider when handling uncertain projects is the method’s ability to update knowledge, enabling managers to learn through the experience gained. Real options and probabilistic methods that implement Bayesian network enable the aggregation of information at each stage of the process (Chin, Tang, Yang, Wong, & Wang, 2009). Finally, an interesting technique of trade-off between immunity to uncertainty and aspirations is the information gap theory model (Regan et al., 2005). This method focuses on the identification of knowledge gaps, uncertainties and risks in order to determine the tolerance for undesirable outcomes.
Based on the literature review and the considerations presented above, we identified four key requirements that PPS methods must meet in order to address radical innovation projects. First, Dynamism, is defined as the characteristic that enables managers to permanently adjust the portfolio according to the evolution of the firm’s guidelines (Kavadias & Chao, 2008, p. 139). Second, Interdependencies, is regarded as the interrelations among projects and their impacts on portfolio performance (i.e. synergy or incompatibilities); several authors suggest that the identification of interdependencies is crucial for innovation projects (Verma & Sinha, 2002; Chien, 2002; Archer & Ghasemzadeh, 1999). Third, Uncertainties, is perceived as situations where neither the outcomes nor the odds could be known (Sommer, Loch, & Pich, 2008). The concept of uncertainty is central to radical innovation. Leifer, O’Connor, and Rice (2001) explain that radical innovation processes involve unprecedented situations and features plenty of technical and market uncertainties (p. 103). Finally, Required input data that refer to the kind of data required by the PPS method. Some authors (e.g. Baker, 1974; Fahrni & Spätig, 1990) consider that financial input data (e.g. estimated costs, profit margin, investment, sales, etc.) imprecise because information will never be precisely available. For Ghasemzadeh and Archer (2000), qualitative information is more recommended for assessing radical innovation projects.
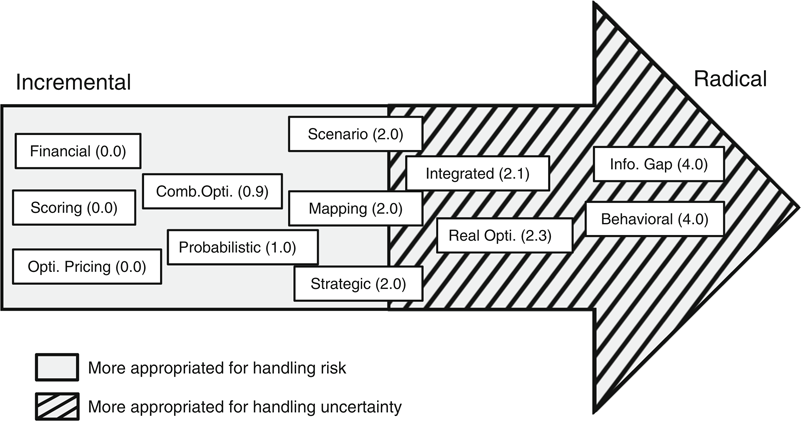
Regarding these four key issues and based on the information provided in the studies, we built a framework (Figure 1). To do so, the approaches identified were analyzed by considering the adequacy between the approaches and the four requirements – we developed a scoring model in which each approach received a point or more if such approach is suitable to one characteristic or more (see Table AI). According to this assessment, behavioral methods and information gap theory are the two approaches more suited for radical innovation, followed by real options and integrated methods. The methods less appropriate for radical innovation are financial methods, options-pricing theory and scoring methods; these approaches are more suitable for incremental innovation (Fahrni & Spätig, 1990).
4.2 Integrated portfolio selection method for radical innovation framework
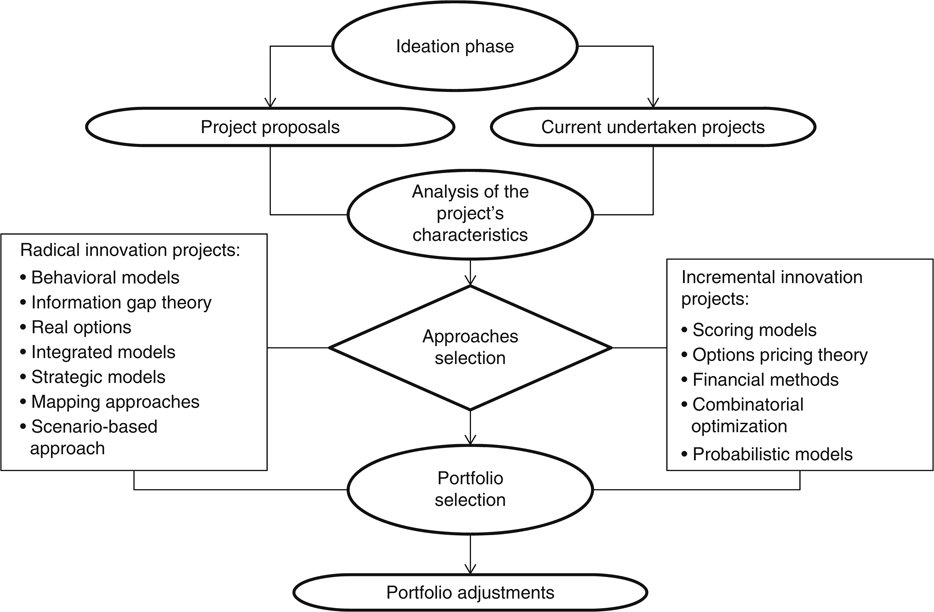
After identifying the advantages and disadvantages of each approach, and identifying the methods more recommended to radical innovation projects, we developed a framework for supporting the PPS selection method according to the innovation level. This framework might help managers to choose and to combine different methods among the alternatives according to a specific innovation level (i.e. radical or incremental innovation).
The framework comprises three phases: ideation phase, which includes the strategic goals, resource constraints and project guidelines; the phase ends with the analysis of the characteristics of the project in which the innovation level is identified. The second phase is the PPS process, where the projects are screened using one or more approaches according to the innovation level. In the last phase, decision makers define the project portfolio based on the recommendations of the selection approaches; this phase also comprises the portfolio adjustments stage, in which managers might include, modify or discard projects in accordance with the environment and the strategic goals. Figure 2 presents the framework suggested.
5. Conclusions and future research
In this paper, we addressed the question of how the selection approaches have evolved to better fit within radical innovation conditions by conducting a systematic literature review. Based on this research approach, we showed how the project selection methods evolved. We present a comprehensive characterization of these methods. We have also identified four key aspects to manage radical innovation portfolios: dynamism, interdependency management, uncertainty treatment and required input data. Based on these findings, we propose a framework for supporting the PPS process according to the innovation level. Moreover, we suggest which PPS approach is more appropriate to incremental and radical innovation projects.
Of course, there is an important opportunity for further studies. We have not discussed in details about how to test our framework. Further studies might test our framework in different industry settings. Also, scholars might test if the methods related to incremental and radical innovation provide superior performance (in relation to the configuration of the portfolio). Scholars might test the best set of methods according to the project’s features (incremental and radical innovation). Finally, scholars might explore empirically how different combinations of methods are more recommended taking into account different industry settings and other features.
| Total | 1974 | 1976 | 1981 | 1985 | 1988 | 1990 | 1992 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | |
| Financial methods | 2 | 1 | 1 | ||||||||||||||||||||||||
| Probabilistic models | 1 | 1 | |||||||||||||||||||||||||
| Options-pricing theory | 1 | 1 | |||||||||||||||||||||||||
| Strategic models | 4 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||
| Scoring models | 3 | 1 | 1 | 1 | |||||||||||||||||||||||
| Comb. optimization | 15 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 2 | 2 | ||||||||||||||
| Behavioral models | 1 | 1 | |||||||||||||||||||||||||
| Mapping approaches | 2 | 1 | 1 | 1 | |||||||||||||||||||||||
| Real options | 3 | 1 | 1 | ||||||||||||||||||||||||
| Integrated models | 13 | 1 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 2 | ||||||||||||||||
| Info. gap theory | 1 | 1 | |||||||||||||||||||||||||
| Scenario-based approach | 2 | 1 | 1 | ||||||||||||||||||||||||
| Total | 48 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 2 | 2 | 3 | 4 | 1 | 1 | 3 | 2 | 1 | 1 | 1 | 2 | 2 | 2 | 1 | 3 | 2 | 5 | 2 |
| Author (year) | Summary | Techniques | Projects | Data required |
| Bard, Balachandra, and Kaufmann (1988) | Projects are assessed in two stages: screened against critical factors and with the other projects. This is achieved through mathematical programming technique that maximizes expected returns | Nonlinear integer programming NPV. Zero-one decision Decision support system (DSS) | Small computer firm specializing in peripheral equipment | Exogenous critical factors (regulations) Project-related variables Financial Data |
| Lal (1974) | Projects are selected according to the cost and benefits and several financial portfolio selection techniques | IRR Marginal social cost Marginal social value NPV Value of marginal product Pareto optimality | Food industry Trade companies Several industrial firms | Expected benefits Financial data Production and external information (trade) |
| Author (year) | Summary | Techniques | Projects | Data required |
| Chin, Tang, Yang, Wong, and Wang (2009) | This methodology assesses new product development risk by Bayesian network with a systematic probability generation and using an NPD project risk network and uncertain variables | Directed acyclic graph (DAG) Conditional probability table (CPT) Bayesian network NPD project risk network Pair-wise comparison matrix | Multinational flashlight manufacturer | Project-related variables Available resources Conditional probabilities Expected benefits Financial data Strategic goals |
| Author (year) | Summary | Techniques | Projects | Data required |
| Galai and Masulis (1976) | This method combines the option pricing model (OPM) with the capital asset pricing model (CAPM) to decide about future investments | Black-scholes Capital asset pricing model CAPM Linear function Economic return (NPV, IRR, ROI, RAI, PBP and EV) Cash flow models European-type options | Two private sector companies | Expected benefits Financial data Production and external information (trade) |
| Author (year) | Summary | Techniques | Projects | Data required |
| Cooper et al.(2002) | Managers define different resources buckets where projects are sorted and prioritized according to these goals: value maximization, balance (long vs short time, or high vs low risk), strategic direction and the right number of projects | Strategic buckets Familiarity matrix | Several large industrial firms | Strategic goals Product lines Project type Scoring criteria Expected benefits Financial data |
| Fahrni and Spätig (1990) | The guidelines are concentrated on the most critical problems, the degree of quantification of relevant factors, interdependencies, consideration of single or multiple objectives and degree of risk and uncertainty | Decision trees Checklists Analytical hierarchy process (AHP) Economic return (NPV, IRR and ROI) Simulation Linear and integer optimization Mathematical programming | Several Swiss firms | Project-related variables Interdependencies Expected benefits Scoring criteria |
| Zeynalzadeh and Ghajari (2011) | The framework considers the firm’s strategy, single project success, portfolio balance and interdependencies. The diamond technique is used to analyze the novelty, technology, complexity and pace | Diamond technique Scoring system | Not informed | Project-related variables Interdependencies Strategic goals Financial data Project success criteria Project competitive advantage |
| Jafarzadeh, Tareghian, Rahbarnia, and Ghanbari (2015) | This method uses reinvesting strategy within a flexible time horizon. In order to maximize gains, the model aims to optimize the combination of projects, time horizon and schedule of projects | Linear and integer optimization Functions and algorithms Nonlinear integer programming | Illustrative example | Project-related and decision variables Strategic goals Time horizon Interdependencies |
| Author (year) | Summary | Techniques | Projects | Data required |
| Cooper (1981) | This method considers the compatibility of resources, the novelty of the project, market competitiveness, technical complexity, competitive strength and economic advantage of the product. It also includes multiple regression analysis to determine the degree of success or failure | Checklists Multiple regression analysis Cross-split-half method Test of predictability | Several large industrial firms | Project-related variables Expected benefits Strategic goals Available resources |
| Hall and Nauda (1990) | An interactive process for R&D selection based on the judgment of key business and technical elements: this approach emphasizes both corporate strategic planning and customer needs | Peer-review/Expert scoring process Experts/Market/Customer Surveys | Department of Defense Aerospace Contractor | Project-related variables Expected benefits Available resources Comparison criteria Strategic goals |
| Henriksen and Traynor (1999) | PPS method based on the ranking of relevance, risk, reasonableness and return. This technique implements an index algorithm which produces a measure of project value as a function of both merit and cost | Scoring algorithm Peer-review scoring process Stakeholder inquiry Delphi technique Linear mapping Value index equation Decision support system (DSS) | Federal Research Laboratory | Project-related variables Expected benefits Comparison criteria Strategic goals |
| Author (year) | Summary | Techniques | Projects | Data required |
| Amiri (2010) | This method uses six criteria to compare investment alternatives through an AHP and fuzzy TOPSIS techniques | Analytical hierarchy process (AHP) Fuzzy TOPSIS Portfolio matrices Delphi technique | National Iranian Oil Company | Project-related variables Expected benefits Strategic goals Financial data |
| Beaujon, Marin and McDonald (2001) | The mathematical model derives from a multidimensional knapsack problem and applies specialized algorithms | Mixed-integer programming (MIP) Linear programming (LP) Manual solution Heuristics Sensitivity Analysis | General Motors R&D Center | Strategic goals Available resources Project-related variables Expected benefits Financial data |
| Doerner, Gutjahr, Hartl, Strauss, and Stummer (2004) | The Ant Colony approach imitates the ants’ behavior to create the shortest and most efficient paths. This method enables the identification of the best configuration for the project portfolio | Multi-objective combinatorial optimization Pareto Ant Colony Optimization Algorithm Quadtree data structure Pareto Simulated Annealing Non-Dominated Sorting Genetic Algorithm (NSGA) | Illustrative example | Project-related variables Interdependencies Expected benefits Financial data Strategic goals Available Resources Synergies among projects |
| Loch and Kavadias (2002) | The method uses marginal analysis to optimally allocate the scarce budget. It considers multiple interacting factors: interdependencies, common resource pool, increasing or decreasing returns, carry-over of the investment benefit over multiple periods, uncertainty and risks | Risk-return matrices Market segment balances Functions and algorithms Weighted average cost of capital (WACC) | Illustrative example based on the diamond industry | Project-related variables Available Resources Expected benefits Financial data Interdependencies Synergies among projects |
| Mandakovic and Souder (1985) | A hierarchical zero-one model of the R&D budgeting process. The authors suggest a flexible or “in-house” objective function that leaves an open option for the users | Multiple-criteria objective functions Economic Return (NPV, IRR, RA, RR and EV) Ad hoc objective function Decomposable interactive algorithm Hierarchical framework Random number generator | Illustrative example | Project-related variables Risk coefficient Expected benefits Probability of success Financial data Available Resources Weighted contribution per project |
| Mohanty, Agarwal, Choudhury, and Tiwari (2005) | The proposed approach simultaneously addresses the issue of combining both monetary and non-monetary aspects using fuzzy set theory to overcome the vagueness in the preferences | Pair-wise comparison matrix Triangular fuzzy numbers Analytical network process (ANP) Fuzzy cost analysis Fuzzy set theory Market/customer surveys Feasibility studies Fuzzy ANP framework Cash flow models Supermatrix | Iron and steel industry in South East Asia | Project-related variables Interdependencies Expected benefits Financial data Strategic goals Available Resources Past projects information Exogenous critical factors |
| Abbassi, Ashrafi, and Tashnizi (2013) | The authors proposed a 0-1 nonlinear mathematical programming method for balancing portfolio following the Markowitz portfolio logic | Cross-entropy algorithm Functions and algorithms Nonlinear integer programming | Illustrative example | Interdependencies Strategic goals Project-related variables Resource constraints Financial data Exogenous critical factors Technological plan |
| Razi and Shariat (2017) | This method consists of hybrid artificial neural network algorithms based on the gray relational analysis (GRA), decision tree and regressions | Grey Relational Algorithm C&R tree (CART) VIKOR Fuzzy TOPSIS Decision matrix Expert opinion questionnaire Sensitivity analysis | Iran Power Plant Repair Company | Strategic goals Project-related variables Evaluation criteria and weighting |
| Ghapanchi, Tavana, Khakbaz, and Low (2012) | The model is a mathematical programming approach used to compare the inputs and outputs of decision-making units (DMU) | Data envelopment analysis (DEA) Fuzzy DEA (FDEA) | Illustrative example: information system/information technology (IS/IT) projects | Interdependencies Strategic goals Evaluation criteria and weighting Project costs Contribution margins Fuzzy risk |
| Pérez, Gómez, Caballero, and Liern (2018) | The method enables the identification of synergies, incompatibilities and other constraints through mathematical programs. It uses fuzzy parameters and adopts several graphics to communicate the results | Fuzzy parameters Mathematical programming | Illustrative example and a real case in a Spanish state university | Project-related variables Financial data Strategic goals Political constraints Available resources Past projects information Time horizon |
| Liesiö, Mild, and Salo (2008) | This method supports PPS through multiple evaluation criteria, advanced portfolio-level benefit-cost analysis and interdependencies identification | Multi-objective zero-one linear programming Interval-valued objective function coefficients Dynamic programming algorithms Portfolio-level benefit-cost analysis Multi-objective zero/one linear programming (MOZOLP) | Illustrative example: technology company | Evaluation criteria and weighting Project-related variables Financial data Strategic goals Resource constraints |
| Hall, Zhuoyu, Qi, and Sim (2015) | This approach uses riskiness indexes, integrates correlations and synergies. The selection is centered on target based choice instead of maximizing returns | Underperformance riskiness index (URI) Entropic underperformance riskiness index (EURI) Benders decomposition techniques Functions and algorithms Sensitivity analysis | Illustrative example (200 projects) | Projects-related variables Multiple objectives and constraints Uncertainties Interdependencies |
| Tavana, Khalili-Damghani, and Abtahi (2013) | This method is a hybrid fuzzy multidimensional multiple-choice Knap-sack problem (MMKP) that helps to define which project is the most indicated under certain circumstances of limited resources | Efficient Epsilon-Constrain (EEC) method Multi-objective evolutionary algorithm Data envelopment analysis (DEA) Fuzzy set theory | Case study: local bank (East Virginia, EEUU.) | Resource constraints Projects-related variables Strategic goals Past projects information |
| Jafarzadeh, Akbari, and Abedin (2018) | Aiming to address simultaneously prioritization, uncertainty and interdependencies, the authors develop a model based on three stages: modeling the problem, house of quality (HOQ) and evaluation of maximal portfolio | Data envelopment analysis (DEA) Fuzzy set theory Quality function development (QFD) Crisp values HOQ matrix | Numerical example of a large-scale Telecommunication Company | Projects-related variables Strategic goals Customer requirements Interdependencies Risk and dependencies among projects Financial data |
| Kalashnikov, Benita, López-Ramos, and Hernández-Luna (2017) | This optimization method considers interdependencies among projects, resource limitations and addresses the problem as a Mixed-integer quadratically constrained programming problem | Lean Six Sigma 0-1 bi-objective quadratic programming problem CPLEX Functions and algorithms Mixed-integer quadratically constrained programming (MIQCP) | Illustrative example | Number of potential projects and related variables Strategic goals Resource constraints Financial data Interdependencies Time required by projects |
| Author (year) | Summary | Techniques | Projects | Data required |
| Han and Diekmann (2001) | Based on the CIA (cross-impact analysis) technique and critical conditions, the interactions among the projects are predicted in order to identify uncertainties and data gaps, enabling decision makers to test combinations to obtain the best project portfolio | Cross-impact analysis Go/No-go decision analysis model Decision makers group | International government projects | Critical conditions Project-related variables Rate impact of the decision strategies Interdependencies |
| Author (year) | Summary | Techniques | Projects | Data required |
| Freedman and Desi (2011) | The DICE framework assesses the risks and probabilities of success of projects. It is based on these factors: duration of the project, the integrity of the team, commitment to change and the effort of stakeholders. This chart distributes the projects into three areas: comfort, risk and uncertainty | BCG’s DICE framework BCG analysis Statistical trend analysis | Power plant | Project-related variables Scoring criteria Expected benefits Financial data Customer data Technical data Strategic goals |
| Wheelwright and Clark (2003) | This method helps to determine which new projects must be adopted and when, how the project set evolves over time and what role each project should play in the overall development effort. This method is useful to identify the gaps, to balance the portfolio and to reveal where development capabilities should be strengthened | Aggregate project plan Bubble diagram Project sequence chart | PreQuip, scientific instruments company | Project-related variables Project types Expected benefits Strategic goals Resources required per project |
| Author (year) | Summary | Techniques | Projects | Data required |
| Luehrman (1998) | In this method, the author explores how option pricing can be used to improve decision making about the sequence and timing of a portfolio of strategic investments. Through the option space, managers can select projects according to the value metrics (value-to-cost and volatility) | Option pricing Option space value-to-cost metric (NPVq) Volatility metric Cash flow models Nested call options | Illustrative example. WeatherIze Corporation (fabrics) | Project-related variables Available resources Expected benefits Financial data Interdependencies Planning periods |
| Wang and Hwang (2007) | A fuzzy set approach for R&D portfolio selection by using real options valuation model. The objective of this method is to maximize the total benefits of the R&D investment portfolio | Fuzzy set theory Zero-one and probabilistic integer programming Crisp mathematical model Option pricing Fuzzy compound option Triangular fuzzy numbers Qualitative possibility theory Geske compound option Volatility metric Newton-Raphson algorithm | An illustrative example from the pharmaceutical industry | Project-related variables Available resources Expected benefits Planning periods Strategic goals |
| Montajabiha, Khamseh, and Afshar-Nadjafi (2017) | The PPS approach applies n-fold compound real options valuations giving flexibility to managers to decide which projects to select. In this method, uncertainty is treated as a range, eliminating the need for statistical distributions | Robust combinatorial optimization algorithm N-fold compound option model Sensitivity analysis Functions and algorithms Robust mixed-integer programming (MIP) | An illustrative example in the pharmaceutical industry | Project-related variables Budget restrictions Estimated financial data Past projects information Strategic goals |
| Author (year) | Summary | Techniques | Projects | Data required | Integrated taxonomies |
| Archer and Ghasemzadeh (1999) | A staged and integrated framework where users are able to select the most suitable techniques for each stage. The approach is divided into three main phases: strategic considerations, individual project evaluation, and portfolio selection. It also has a stage of portfolio adjustment whereby users can make some changes | Economic return (NPV, IRR and ROI) CAPM (capital asset pricing model) Work breakdown structure (WBS) Monte Carlo simulation Bayesian statistical theory Market research Ad hocapproaches based on scoring Q-sort Portfolio matrices | Experimental tests | Project-related variables Scoring criteria Expected Benefits Strategic goals Financial Data Interdependencies | Strategic Financial Scoring Mapping Combinatorial optimization Probabilistic Behavioral |
| Chien (2002) | The approach has three phases: identification of objectives of the portfolio, construction of scales to measure portfolio attributes, and measurement of alternative portfolios. The model focuses on the identification and exploitation of the interrelations among projects | Work breakdown structure (WBS) Value/utility functions MAV/MAU models Linear programming (LP) | An illustrative example based on the project: American stop smoking intervention study by The National Cancer Institute | Project-related variables Scoring criteria Expected Benefits Financial data Strategic goals Interdependencies | Scoring Combinatorial optimization Behavioral |
| Coldrick, Longhurst, Ivey, and Hannis (2005) | This staged method is an extension of Lockwood’s (1999)work in which the selection process is divided into project evaluation (single projects), project selection (examining a range of projects), and application to the different types of research | Checklists Delphi technique Scoring table layout Risk/reward assessment Bubble diagram Risk analysis Economic return (NPV, IRR, CBA, DCF and PVI) | Gas turbine project | Project-related variables Scoring criteria Expected Benefits Strategic goals Financial data | Combinatorial optimization Scoring Behavioral Mapping Financial |
| Cooper, Edgett, and Kleinschmidt (2000) | In this evolved version of the Stage Gate System®, the two-parts decision gates (Go/Kill) were incorporated, and also a formal stage where projects are force-ranked against one another | Strategy buckets approach Bubble diagrams Prioritized scored list Economic return (NPV, IRR and EV) Checklists | Several large industrial firms | Project-related variables Scoring criteria Expected benefits Financial data Strategic goals | Strategic Financial Scoring Mapping |
| Dutra, Ribeiro, and Carvalho (2014) | An economic-probabilistic model that combines financial and probabilistic approaches to consider uncertainties, incorporate multiple criteria, and to adjust the method in response to changes in the business environment | Economic return (NPV, IRR, RA, RR and EV) PayBack period Monte Carlo Decision Support System (DSS) Triangular distribution | Power distribution company | Project-related variables Scoring criteria Expected benefits Financial data Strategic goals | Financial Probabilistic |
| Ghasemzadeh and Archer (2000) | An evolution of the integrated framework for project portfolio selection (1999). The authors set up the project analysis and selection system (PASS), an organized framework for portfolio selection through a decision support system (DSS) | Economic return (NPV, IRR, ROI and RAI) Analytical hierarchy process (AHP) Decision support system (DSS) Group support system (GSS) Expert choice Integer linear programming Ad hocapproaches based on scoring Gantt Chart Portfolio matrices | Experimental tests with two high-tech companies | Project-related variables Scoring criteria Interdependencies Expected benefits Strategic goals Financial data | Strategic Financial Scoring Mapping Combinatorial optimization Probabilistic Behavioral |
| Linton, Walsh, and Morabito (2002) | This dual method uses a multi-criteria decision-making model and a graphical decision support system that enables the integration of objective and subjective methods for analysis and selection. This approach is ideal for reducing a large number of projects | Data envelopment analysis (DEA) Value creation model (VCM) Parabox representation Nicheworks depiction | Advanced technology division of bell laboratories | Project-related variables Stage of the intellectual property lifecycle Expected benefits Financial data Strategic goals | Scoring Mapping Combinatorial optimization |
| Loch, Pich, Terwiesch, and Urbschat (2001) | This methodology comprises the identification of target contributions, project expectations, and needs. Projects are selected by mixed-integer linear programming. This approach focuses on qualitative data such as the criteria, project contributions and gaps | Matrix of evaluation criteria Mixed-integer programming (MIP) Linear programming (LP) Checklists | R&D at BMW | Project-related variables Interdependencies Scoring criteria Expected benefits Financial data Strategic goals | Scoring Mapping Combinatorial optimization |
| Medaglia, Graves, and Ringuest (2007) | An evolutionary method which includes multiple objectives, project interdependencies and linear structure for resource constraints. The method is ideal for partially funded projects, multiple objectives, uncertainties, project interdependencies, and linearly-constrained resources | Parameter space investigation method (PSI) Black Box approach Pareto solution Multi-objective evolutionary algorithms (MOEA) Monte Carlo simulation | Experimental tests | Project-related variables Scoring criteria Expected benefits Financial data Interdependencies | Combinatorial optimization Probabilistic |
| Jeng and Huang (2015) | The method consists of an integrated approach based on a hybrid MCDM, modified Delphi, a DEMATEL method and an analytic network process. The objective is to overcome the complexity of interdependences and feedbacks between criteria and alternatives | Modified Delphi method Need solution differentiation and benefits (NSDB) framework DEMATEL method ANP | National research institute | Strategic goals Evaluation criteria Potential customer requirements | Combinatorial optimization Strategic Behavioral |
| Xidonas, Doukas, Mavrotas, and Pechak (2016) | This approach incorporates environmental criteria and uses a bi-objective programming model. In order to handle uncertainties, the model uses the iterative trichotomic approach (ITA) combined with multi-objective problems and Monte Carlo simulations | Multi-objective integer programming (MOIP) Pareto solution Monte Carlo simulation Functions and algorithms Stochastic multi-objective acceptability analysis (SMAA) | 40 large firms | Financial data Projects-related variables Multiple objectives and constraints Conditional probabilities Expected Benefits Uncertainties | Combinatorial optimization Probabilistic |
| Ei-Kholany and Abdelsalam (2017) | This method combines a multi-objective binary cuckoo search (MOCS) algorithm with Monte Carlo simulation to support the PPS decision. Uncertainties are handled via Monte Carlo simulation to translate risk into quantitative data | Monte Carlo simulation MOCS Fuzzy parameters Mathematical programming Functions and algorithms Meta-heuristic algorithm Binary cuckoo search Pareto solution | Illustrative example (40 projects) | Criteria and performance values Project-related variables Multiple-objective parameters | Combinatorial optimization Probabilistic |
| Hu and Szmerekovsky (2017) | On the basis of limited resources and the Newsvendor problem perspective, the authors develop a set of procedures and heuristics to provide managerial guidelines in the portfolio selection process. The aim of the model is to find the ideal projects, avoiding cost overruns and budgetary slack | Functions and algorithms Sensitivity analysis Evolutionary solution method (Excel solver) Heuristics based on projects ratio and profit ratio | Numerical example | Number of potential projects and related variables Strategic goals Resource constraints Financial data Budget by project | Combinatorial optimization Strategic |
| Author (year) | Summary | Techniques | Projects | Data required |
| Regan, Ben-Haim, Wilson, Lundberg, Andelman, and Burgman (2005) | This method uses information gap theory to propagate uncertainties, by establishing a tolerance threshold to rank management options and to cut off pernicious options. This approach includes three elements: a mathematical process model, a performance requirement and a model for uncertainty | Robustness Function Decision table (utilities and probabilities) EV Robustness curves | Decision problem for conservation area of the Sumatran Rhino | Project-related variables Positive and negative expected outcomes |
| Author (year) | Summary | Techniques | Projects | Data required |
| Liesiö and Salo (2012) | This method offers interactive decision support for rejection and selection of projects, which uses scenarios probabilities and utility functions. The method uses MOZOLP to identify the non-dominated portfolios which satisfy criteria such as resource and feasibility constraints | Multi-objective zero/one linear programming (MOZOLP) Functions and algorithms Experts opinion survey Risk utility function Tornado plots Conditional value at risk (CVaR) | An illustrative example at the International Institute for Applied Systems Analysis (IIASA) | Project-related variables Experts’ estimates (risk preferences/feasible scenarios) Time horizon |
| Zhang, Yang, Dou, and Jiang (2016) | The authors proposed a scenario-based approach to select army engineering and manufacturing development projects under incomplete scenario information and interdependency constraints. The method is based on a multi-objective programming model | Scenario-based programming Functions and algorithms Pair-wise comparison matrix Hidden Markov models (HMMs) | An illustrative example of army engineering and manufacturing development project | Experts’ estimates (risk preferences/feasible scenarios) Financial data Project-related variables |
| Document | Method | Dynamism | Interdependencies | Input data | Uncertainty | Total | Mean per method |
| Bard et al.(1988) | Financial methods | 0 | 0 | 0 | 0 | 0 | 0.0 |
| Lal (1974) | Financial methods | 0 | 0 | 0 | 0 | 0 | |
| Chin et al.(2009) | Probabilistic Models | 0 | 0 | 0 | 1 | 1 | 1.0 |
| Galai and Masulis (1976) | Opt. pricing theory | 0 | 0 | 0 | 0 | 0 | 0.0 |
| Cooper and Kleinschmidt (2002) | Strategic models | 1 | 0 | 0 | 0 | 1 | 2.0 |
| Fahrni and Spätig (1990) | Strategic models | 1 | 1 | 0 | 0 | 2 | |
| Zeynalzadeh and Ghajari (2011) | Strategic models | 1 | 1 | 0 | 0 | 2 | |
| Jafarzadeh et al.(2015) | Strategic models | 1 | 1 | 1 | 0 | 3 | |
| Cooper (1981) | Scoring models | 0 | 0 | 0 | 0 | 0 | 0.0 |
| Hall and Nauda (1990) | Scoring models | 0 | 0 | 0 | 0 | 0 | |
| Henriksen and Traynor (1999) | Scoring models | 0 | 0 | 0 | 0 | 0 | |
| Amiri (2010) | Combinatorial opt. | 0 | 0 | 0 | 0 | 0 | 0.9 |
| Beaujon et al. (2001) | Combinatorial opt. | 0 | 0 | 0 | 0 | 0 | |
| Doerner et al. (2004) | Combinatorial opt. | 0 | 1 | 0 | 1 | 2 | |
| Loch and Kavadias (2002) | Combinatorial opt. | 0 | 1 | 0 | 0 | 1 | |
| Mandakovic and Souder (1985) | Combinatorial opt. | 1 | 0 | 0 | 0 | 1 | |
| Mohanty et al.(2005) | Combinatorial opt. | 0 | 0 | 0 | 0 | 0 | |
| Abbassi et al. (2013) | Combinatorial opt. | 0 | 1 | 0 | 0 | 1 | |
| Razi and Shariat (2017) | Combinatorial opt. | 0 | 0 | 0 | 0 | 0 | |
| Ghapanchi et al.(2012) | Combinatorial opt. | 0 | 1 | 0 | 0 | 1 | |
| Pérez et al.(2018) | Combinatorial opt. | 0 | 1 | 0 | 0 | 1 | |
| Liesiö et al. (2008) | Combinatorial opt. | 0 | 1 | 0 | 1 | 2 | |
| Hall et al.(2015) | Combinatorial opt. | 0 | 1 | 0 | 0 | 1 | |
| Tavana et al. (2013) | Combinatorial opt. | 0 | 0 | 0 | 0 | 0 | |
| Jafarzadeh et al.(2018) | Combinatorial opt. | 0 | 1 | 0 | 1 | 2 | |
| Kalashnikov et al.(2017) | Combinatorial opt. | 0 | 1 | 0 | 0 | 1 | |
| Han and Diekmann (2001) | Behavioral models | 1 | 1 | 1 | 1 | 4 | 4.0 |
| Freedman and Desi (2011) | Mapping app. | 1 | 0 | 0 | 0 | 1 | 2.0 |
| Wheelwright and Clark (2003) | Mapping app. | 1 | 0 | 1 | 1 | 3 | |
| Luehrman (1998) | Real options | 1 | 1 | 1 | 0 | 3 | 2.3 |
| Wang and Hwang (2007) | Real options | 1 | 0 | 0 | 1 | 2 | |
| Montajabiha et al.(2017) | Real options | 1 | 0 | 0 | 1 | 2 | |
| Archer and Ghasemzadeh (1999) | Integrated models | 1 | 1 | 1 | 1 | 4 | 2.1 |
| Chien (2002) | Integrated models | 0 | 1 | 1 | 1 | 3 | |
| Coldrick et al. (2005) | Integrated models | 1 | 0 | 0 | 1 | 2 | |
| Cooper et al. (2000) | Integrated models | 0 | 0 | 0 | 0 | 0 | |
| Dutra et al. (2014) | Integrated models | 1 | 0 | 0 | 1 | 2 | |
| Ghasemzadeh and Archer (2000) | Integrated models | 1 | 1 | 1 | 1 | 4 | |
| Linton et al. (2002) | Integrated models | 1 | 1 | 0 | 1 | 3 | |
| Loch et al.(2001) | Integrated models | 1 | 1 | 0 | 0 | 2 | |
| Medaglia et al.(2007) | Integrated models | 1 | 1 | 0 | 1 | 3 | |
| Jeng and Huang (2015) | Integrated models | 1 | 1 | 0 | 0 | 2 | |
| Xidonas et al. (2016) | Integrated models | 0 | 0 | 0 | 1 | 1 | |
| Ei-Kholany and Abdelsalam (2017) | Integrated models | 0 | 0 | 0 | 1 | 1 | |
| Hu and Szmerekovsky (2017) | Integrated models | 0 | 0 | 0 | 0 | 0 | |
| Regan et al. (2005) | Info. gap theory | 1 | 1 | 1 | 1 | 4 | 4.0 |
| Liesiö and Salo (2012) | Scenario-based | 1 | 0 | 1 | 0 | 2 | 2.0 |
| Zhang et al. (2016) | Scenario-based | 1 | 1 | 0 | 0 | 2 |
Appendix
Table AI
References
Abbassi, M., Ashrafi, M., & Tashnizi, E. (2013). Selecting balanced portfolios of R&D projects with interdependencies: a cross-entropy based methodology. Technovation, 34(1), 54–63.
Amiri, M. P. (2010). Project selection for oil-fields development by using the AHP and fuzzy TOPSIS methods. Expert Systems with Applications, 37(9), 6214–6224.
Archer, N. P., & Ghasemzadeh, F. (1999). An integrated framework for project portfolio selection. International Journal of Project Management, 17(4), 207–2016.
Baker, N. R. (1974). R&D Project selection models: an assessment. IEEE Transactions on Engineering Management, 21(4), 165–170.
Bard, J. F., Balachandra, R., & Kaufmann, P. E. (1988). An interactive approach to R&D project selection and termination. IEEE Transactions on Engineering Management, 35(3), 139–146.
Beaujon, G. J., Marin, S. P., & McDonald, G. C. (2001). Balancing and optimizing a portfolio of R&D projects. Naval Research Logistics, 48(1), 18–40.
Brasil, V., Salerno, M., & Gomes, L. A. V. (2018, July–September). Valuation of innovation projects with high uncertainty: reasons behind the search of real options. Journal of Engineering and Technology Management, 49, 109–122.
Briner, R. B., & Denyer, D. (2010), Systematic review and evidence synthesis as a practice and scholarship tool. In D. Rousseau (Ed.), Handbook of Evidence-Based Management: Companies, Classrooms and Research (pp. 112–129). Oxford: Oxford University Press.
Chien, C. (2002). A portfolio-evaluation framework for selecting R&D projects. R&D Management, 32(4), 359–368.
Chin, K., Tang, D., Yang, J., Wong, S., & Wang, H. (2009). Assessing new product development project risk by Bayesian network with a systematic probability generation methodology. Expert Systems with Applications, 36(6), 9879–9890.
Coldrick, S., Longhurst, P., Ivey, P., & Hannis, J. (2005). An R&D options selection model for investment decisions. Technovation, 25(3), 185–193.
Cooper, R. G. (1981). An empirically derived new product project selection model. IEEE Transactions on Engineering Management, 28(3), 54–61.
Cooper, R. G. (1993). Winning at New Products: Accelerating the Process from Idea to Launch. MA: Addison-Wesley.
Cooper, R. G., Edgett, S. J., & Kleinschmidt, E. J. (1999). New product portfolio management: practices and performance. Journal of Production Innovation Management, 16(4), 333–351.
Cooper, R. G., Edgett, S. J., & Kleinschmidt, E. J. (2000). New problems, new solutions: making portfolio management more effective. Research-Technology Management, 43(2), 18–33.
Cooper, R. G., Edgett, S. J., & Kleinschmidt, E. J. (2002). Portfolio management-fundamental to new product success. In P. Belliveau, A. Griffin, & S. Somermeyer (Eds), PDMA ToolBook for New Product Development (pp. 331–347). New York, NY: John Wiley & Sons.
Doerner, K., Gutjahr, W. J., Hartl, R., Strauss, C., & Stummer, C. (2004). Pareto ant colony optimization: a metaheuristic approach to multiobjective portfolio selection. Annals of Operations Research, 131(1-4), 79–99.
Dutra, C., Ribeiro, J. L., & Carvalho, M. (2014). An economic-probabilistic model for project selection and prioritization. International Journal of Project Management, 32(6), 1042–1055.
Ei-Kholany, M. M. S., & Abdelsalam, H. M. (2017). Multi-objective binary cuckoo search for constrained project portfolio selection under uncertainty. European Journal of Industrial Engineering, 11(6), 818–853.
Fahrni, P., & Spätig, M. (1990). An application-oriented guide to R&D project selection and evaluation methods. R&D Management, 20(2), 155–171.
Freedman, M., & Desi, R. (2011). Large-Project Management, A Blueprint for Success. The Boston Consulting Group. Available from: www.bcg.com/documents/file76656.pdf
Galai, D., & Masulis, R. W. (1976). The option pricing model and the risk factor of stock. Journal of Financial Economics, 3(1-2), 53–81.
Ghapanchi, A., Tavana, M., Khakbaz, M., & Low, G. (2012). A methodology for selecting portfolios of projects with interactions and under uncertainty. International Journal of Project Management, 30(7), 791–803.
Ghasemzadeh, F., & Archer, N. P. (2000). Project portfolio selection through decision support. Decision Support Systems, 29(1), 73–88.
Hall, D. L., & Nauda, A. (1990). An interactive approach for selecting IR&D projects. IEEE Transactions on Engineering Management, 37(2), 126–133.
Hall, N. G., Zhuoyu, D., Qi, J., & Sim, M. (2015). Managing underperformance risk in project portfolio selection. Operations Research, 63(3), 660–675.
Han, S. H., & Diekmann, J. E. (2001). Approaches for making risk-based go/no-go decision for international projects. Journal of Construction Engineering and Management, 127(4), 300–3008.
Henriksen, A. D., & Traynor, A. J. (1999). A practical R&D project-selection scoring tool. IEEE Transactions on Engineering Management, 46(2), 158–170.
Hu, Q., & Szmerekovsky, J. (2017). Project portfolio selection: a newsvendor approach. Decision Sciences, 48(1), 176–199.
Jafarzadeh, M., Akbari, P., & Abedin, B. (2018, November). A methodology for project portfolio selection under criteria prioritisation, uncertainty and projects interdependency – combination of fuzzy QFD and DEA. Expert Systems with Applications, 110, 237–249.
Jafarzadeh, M., Tareghian, H.R., Rahbarnia, F., & Ghanbari, R. (2015). Optimal selection of project portfolios using reinvestment strategy within a flexible time horizon. European Journal of Operational Research, 243(2), 658–664.
Jeng, D., & Huang, K. (2015). Strategic project portfolio selection for national research institutes. Journal of Business Research, 68(11), 2305–2311.
Kalashnikov, V., Benita, F., López-Ramos, F., & Hernández-Luna, A. (2017, April). Bi-objective project portfolio selection in Lean Six Sigma. International Journal of Production Economics, 186, 81–88.
Kavadias, S., & Chao, R. O. (2008), “Resource allocation and new product development portfolio management. In C. H. Loch, & S. Kavadias (Eds.), Handbook of New Product Development Management (pp. 135–163). Oxford: Butterworht-Heinemann.
Lal, D. (1974). Methods of project analysis: A review, New York, NY: International Bank For Reconstruction and Development.
Leifer, R., O’Connor, G., & Rice, M. (2001). Implementing radical innovation in mature firms: the role of hubs. The Academy of Management Executive, 15(3), 102–113.
Liesiö, J., & Salo, A. (2012). Scenario-based portfolio selection of investment projects with incomplete probability and utility information. European Journal of Operational Research, 217(1), 162–172.
Liesiö, J., Mild, P., & Salo, A. (2008). Robust portfolio modeling with incomplete cost information and project interdependencies. European Journal of Operational Research, 190(3), 679–695.
Linton, J. D., Walsh, S. T., & Morabito, J. (2002). Analysis, ranking and selection of R&D projects in a portfolio. R&D Management, 32(2), 139–148.
Loch, C. H., & Kavadias, S. (2002). Dynamic portfolio selection of NPD programs using marginal returns. Management Science, 48(10), 1227–1241.
Loch, C. H., Pich, M. T., Terwiesch, C., & Urbschat, M. (2001). Selecting R&D projects at BMW: a case study of adopting mathematical programming models. IEEE Transactions on Engineering Management, 48(1), 70–80.
Lockwood, C. (1999). Comparison of average-passage equation closures through simulation of single and multi-row axial compressors; the limitations of using a commercial CFD code (PhD thesis). Cranfield University.
Luehrman, T. (1998). Strategy as a portfolio of real options. Harvard Business Review (pp. 89–99). September–October.
Mandakovic, T., & Souder, W. E. (1985). A flexible hierarchical model for project selection and budget allocation. R&D Management, 15(1), 23–29.
Medaglia, A. L., Graves, S. B., & Ringuest, J. L. (2007). A multiobjective evolutionary approach for linearly constrained project selection under uncertainty. European Journal of Operational Research, 179(3), 869–894.
Mohanty, R. P., Agarwal, R., Choudhury, A. K., & Tiwari, M. K. (2005). A fuzzy ANP-based approach to R&D project selection: a case study. International Journal of Production Research, 43(24), 5199–5216.
Montajabiha, M., Khamseh, A., & Afshar-Nadjafi, B. (2017). A robust algorithm for project portfolio selection problem using real options valuation. International Journal of Managing Projects in Business, 10(2), 386–403.
Mun, J. (2005). Real Options Analysis: Tools and Techniques. NJ: Wiley.
Pérez, F., Gómez, T., Caballero, R., & Liern, V. (2018, June). Project portfolio selection and planning with fuzzy constraints. Technological Forecasting & Social Change, 131, 117–129.
Razi, F. F., & Shariat, S. H. (2017). A hybrid grey based artificial neural network and C&R tree for project portfolio selection. Benchmarking: An International Journal, 24(3), 651–665.
Regan, H., Ben-Haim, Y., Wilson, W., Lundberg, P., Andelman, S., & Burgman, M. (2005). Robust decision-making under severe uncertainty for conservation management. Ecological Applications, 15(4), 1471–1477.
Rice, M. P., O’Connor, G. C., & Pierantozzi, R. (2008). Implementing a learning plan to counter project uncertainty. MIT Sloan Management Review, 49(2), 54–62.
Shoemaker, P. (1995). Scenario planning: a tool for strategic thinking. MIT Sloan Management Review, 36(2), 25–40.
Sommer, S. C., Loch, C. H., & Pich, M. T. (2008). Project risk management in new product development. In C. H. Loch, & S. Kavadias (Eds), Handbook of New Product Development Management (pp. 439–465). Oxford: Butterworht-Heinemann.
Tavana, M., Khalili-Damghani, K., & Abtahi, A. (2013). A fuzzy multidimensional multiple-choice knapsack model for project portfolio selection using an evolutionary algorithm. Annals of Operations Research, 206(1), 449–483.
Verma, D., & Sinha, K. (2002). Toward a theory of project interdependencies in high tech R&D environments. Journal of Operations Management, 20(5), 451–468.
Wang, J., & Hwang, W. (2007). A fuzzy set approach for R&D portfolio selection using a real options valuation model. The International Journal of Management Science, 35(3), 247–257.
Wheelwright, S.C., & Clark, K.B. (2003). Creating project plan to focus product development. Harvard Business Review (pp. 1–14). September–October.
Xidonas, P., Doukas, H., Mavrotas, G., & Pechak, O. (2016). Environmental corporate responsibility for investments evaluation: an alternative multi-objective programming model. Annals of Operations Research, 247(2), 395–413.
Zeynalzadeh, R., & Ghajari, A. (2011). A framework for project portfolio selection with risk reduction approach. African Journal of Business Management, 5(26), 10474–10482.
Zhang, P., Yang, K., Dou, Y., & Jiang, J. (2016). Scenario-based approach for project portfolio selection in army engineering and manufacturing development. Journal of Systems Engineering and Electronics, 27(1), 166–176.
Further reading
Howell, D., Whindahl, C., & Seidel, R. (2010). A project contingency framework based on uncertainty and its consequences. International Journal of Project Management, 28(3), 256–264.
Lynn, G. S., Morone, J. G., & Paulson, A. S. (1996). Marketing and discontinuous innovation: the probe and learn process. California Management Review, 38(3), 8–37.
Pich, M. T., Loch, C. H., & De Meyer, A. (2002). On uncertainty, ambiguity, and complexity in project management. Management Science, 48(8), 1008–1023.
Shane, S., & Ulrich, C. (2004, February). Technological innovation, product development, and entrepreneurship in management science. Management Science, 50, 133–154.

