Resumen: Este artículo expone los conceptos básicos de las pruebas de ADN en el contexto forense. Describe como se establece la coincidencia entre el perfil genético de la muestra biológica encontrado en la escena del crimen con el perfil de un sospechoso o imputado; como se estima la probabilidad de que la coincidencia haya sido por azar evaluando la frecuencia del perfil genético en la población, es decir, la probabilidad de que el sospechoso en realidad no haya sido la fuente de la evidencia; y otros parámetros estadísticos importantes al momento de evaluar un análisis de ADN.
Palabras clave: Genética Forense, Perfil genético, Marcadores moleculares, STRs.
Abstract: This article exposes the basic concepts of DNA testing in the forensic context. We describe some historical aspects of how these genetic tests were carried out at the beginning, the STR markers analyzed to obtain DNA profiles, the equipment and the commercially available human identification kits that are most used in forensic genetics laboratories. To conclude this review, we describe how the interpretation process of genetic profiles is begun.
Keywords: Forensic genetics, DNA profile, molecular markers: CODIS, STRs.
Trabajos de Revisión
Lo que se debe saber acerca de……… Las pruebas de ADN en el contexto forense parte II. Interpretación estadística
Basic concepts of DNA testing in the forensic context part II. Statistical interpretation.
Recepción: 03 Julio 2018
Aprobación: 20 Noviembre 2018
Autor de correspondencia: hrangel13@hotmail.com

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.
En el artículo anterior (Villalobos-Rangel H. Las pruebas de ADN en el contexto forense. Rev. cienc. forenses Honduras. 2017; 3(2): 27-37), abordamos el planteamiento general para interpretar los casos criminales, teniendo como ejemplo que si en Jalisco, México, un desconocido cometió un crimen y deja evidencia biológica en el lugar de los hechos, por ejemplo, sangre, semen, saliva, etc. Después se detiene aun sospechoso que se cree está relacionado con el crimen. El laboratorio obtiene los perfiles genéticos de la evidencia y los compara con los del sospechoso. Si no coinciden, el juez, analizando la información del caso–tanto genética como no genética podría exonerar al inculpado de su participación en el crimen1,2. Por el contrario, cuando coinciden, comienza un proceso de interpretación que inicialmente responde a la pregunta: ¿Cuál es la probabilidad de encontrar ese perfil genético en la población general?, con lo que se puede estimar la probabilidad de involucrar a un inocente en el crimen. La respuesta requiere aplicar conceptos de genética poblacional, ya que para la estimación se deben conocer las frecuencias alélicas de los STRs empleadas en la prueba de ADN para la población donde ha ocurrido el crimen2; en el ejemplo que nos ocupa, Jalisco, México. Además, es necesario determinar algunos parámetros estadísticos de interés forense en la población donde se aplican los STRs.
Para realizar la evaluación estadística de un caso criminal se realizan una serie de pasos3,4:
1.- Primero se establece la coincidencia entre el perfil genético de la muestra biológica encontrado en el indicio, evidencia o escena del crimen con el perfil del sospechoso o imputado.
2.- Se estima la probabilidad de que la coincidencia haya sido por azar evaluando la frecuencia del perfil genético en la población, es decir, la probabilidad que el sospechoso en realidad no haya sido la fuente de la evidencia; para ello se estima la frecuencia de los genotipos para cada STR del perfil genético, usando las frecuencias de los alelos involucrados. Lo ideal es que en la población donde sucedió el crimen se hayan estimado las frecuencias alélicas y verificado que la distribución de genotipos se ajusta al equilibrio Hardy-Weinberg (EHW), así como que los marcadores STRs no se asocien entre sí, demostrando -en términos genéticos que no están en desequilibrio de ligamiento (DL). El EHW facilita estima frecuencia de genotipos heterocigotos con la fórmula 2pq, mientras que en homocigotos la fórmula que se aplica es p2; donde p y q representan las frecuencias de los alelos del genotipo, como se muestra en laFigura 1 yCuadro 1. Cabe mencionar que cuando no se cuenta con las frecuencias de la población donde sucedió el crimen, podrían usarse las de una población relacionada (p. ejem. latinoamericana, africo- americana, etc.) o geográficamente cercana (p. ejem. Honduras y El Salvador).
3.-Luego se multiplican las frecuencias genotípicas estimadas, cuyo resultado representa la frecuencia del perfil genético. A este sencillo proceso de multiplicar se le describe como la regla del producto, y es correcto hacerlo cuando se descartó el DL entre cada par de STRs. El resultado es correspondiente a la probabilidad de coincidencia al azar (PCA), o sea la probabilidad que esa combinación genética (genotipo), se presente producto del azar, este parámetro también se conoce por sus siglas en inglés como RMP (random matching probability).
4.- Finalmente, el inverso de la PCA constituye la razón de verosimilitud (LR= 1/PCA), también conocida por sus siglas en inglés como LR (likelihood ratio) (Figura 1; Tabla 1). Sin embargo, el genetista forense no debe preocuparse por estos aspectos, ya que estos datos genético-poblacionales (frecuencias alélicas, EHW y DL) están descritos en la literatura científica.
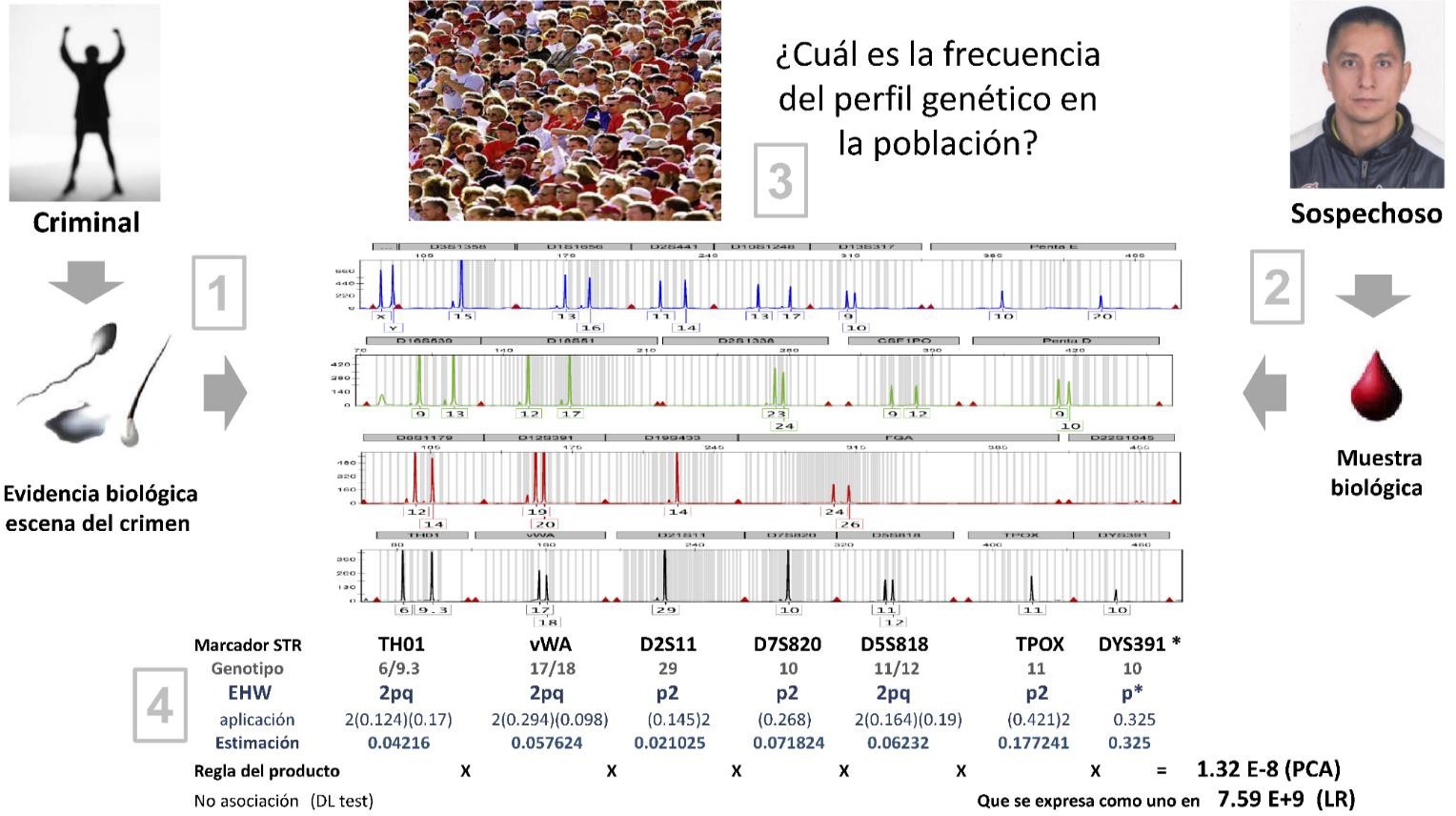
Representación del proceso de evaluación estadística de un caso criminal, donde se compara el perfil genético de la evidencia con el del sospechoso, que en el ejemplo coinciden (iguales).
Probabilidad de coincidencia al azar (PCA)= 32x10-8=0,0000000132 Likehood ratio (LR) = 1/1,32x10-8= 75,757,575Ahora, describiremos el significado de los parámetros de importancia para interpretarlos en un juzgado. Hay que considerar que el LR compara las probabilidades de dos hipótesis mutuamente excluyentes: La del fiscal (Hf) contra la de la defensa (Hd), LR=Hf/Hd4. El LR es un valor numérico que representa el peso de la evidencia genética; mientras más grande el LR, más potente es la evidencia genética para relacionar al inculpado y/o la evidencia con el crimen.5,6,7,8
La hipótesis del fiscal-Hf indica que la probabilidad de que el perfil genético de la evidencia haya coincidido con el del sospechoso asumiendo que SÍ está implicado; por lo tanto, la probabilidad es uno (100%). En contraparte, la hipótesis de la defensa-Hd asume que el sospechoso NO está implicado, por lo que representa la probabilidad que haya coincidido al azar (PCA) calculada a partir del perfil genético. Lo anterior entonces se puede resumir como:
LR= Hf/Hd = 1/PCA; en el ejemplo del Cuadro 1: LR= 3.70042E+12
En el ejemplo arriba descrito, el LR indica a cuántas personas se estima se tendría que analizar para encontrar por azar un perfil genético igual al del sospechoso.
Integración de la evidencia genética al caso.
El consenso de expertos y las recomendaciones a nivel internacional, indican que debe aplicarse la estadística bayesiana o sea integrar a la evidencia genética, otra información no genética. Cabe recordar que el Teorema de Bayes sirve para estimar una probabilidad final de un evento a partir de una probabilidad inicial, pero añadiendo nueva evidencia, en este caso evidencia genética derivada del perfil genético condensado en un valor numérico (LR)3-5. La fórmula es la siguiente:
Odds posteriori = LR (ADN) x odds a priori (información no genética)
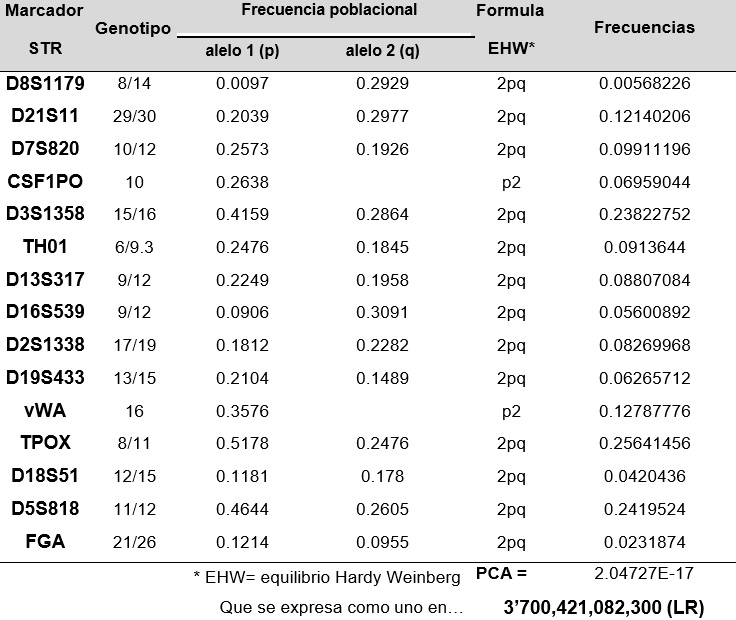
Evaluación estadística de un perfil genético X de 15 STRs asumiendo el equilibrio Hardy- Weinberg (EHW), las frecuencias alélicas y la regla del producto para obtener la probabilidad de coincidencia al azar (PCA) y el LR, aplicable a un caso criminal.
Para entender la genética bayesiana cabe aclarar dos diferencias fundamentales respecto a la estadística clásica o frecuentista4:
1) ODDS: las probabilidades de los eventos se miden a manera de apuesta, denominados odds. Un odds mide cuantas veces es más probable una propuesta (hipótesis) respecto a otra, donde ambas son exhaustivas (no hay más) y excluyentes una de la otra, por ejemplo: ganar/perder; culpable/inocente; es el padre/no es el padre, etc. Un ejemplo sencillo, ¿cuáles son los odds de ganar al tirar un dado, considerando que gano si me sale tres? Se expresaría así: Odds (3/no 3) = 1/5,es decir, solo hay una opción de ganar y cinco de perder. Otra forma de decirlo es que tienes 5 veces más posibilidades de perder que de ganar.
2) ES SUBJETIVA: A la estadística bayesiana también se le llama subjetivista porque, a diferencia de la probabilidad frecuentista donde la probabilidad de que me salga un 2 al tirar un dado tiene una probabilidad definida (Pr (2)=1/6), en la estadística bayesiana se asignan probabilidades. Por ejemplo, si me preguntan ¿cuál es la probabilidad de que gane el equipo de futbol de Brasil jugando contra México? Entonces Joao (brasileño) le asignaría un odds de 30 a uno a favor de que gana Brasil. Es decir, odds (gana/pierde) = 30/1. Por el contrario, sus odds de que gane México sería entonces 1/30 =0.033. Sin embargo, un fan mexicano que todos los domingos ve el futbol en televisión posiblemente habría asignado unos odds diferente, es decir, a favor de México.
Ahora habría que preguntarnos si abordar las situaciones de identificación humana o criminalísticas bajo esta lógica subjetiva (bayesiana) es adecuado. Se considera que sí, ya que muchas situaciones de la vida real son demasiado efímeras y complejas, por lo que no puede aplicarse la estadística frecuentista. Por ejemplo, en el ámbito legal, lo que sí sería erróneo es sentenciar a alguien porque uno de cada tres (1/3) de los acusados de violación son culpables y –desgraciadamente– el acusado del ejemplo fue el tercero que llegó y los dos primeros fueron inocentes! De igual forma descartar una paternidad dado que en aproximadamente una de cada cuatro pruebas el padre no lo es (25%), lo que se denomina exclusión. La ventaja de la estadística bayesiana es que permite abordar situaciones complejas, donde no hay forma de aplicar la estadística tradicional, siguiendo un razonamiento y una lógica para llegar a conclusiones razonables.
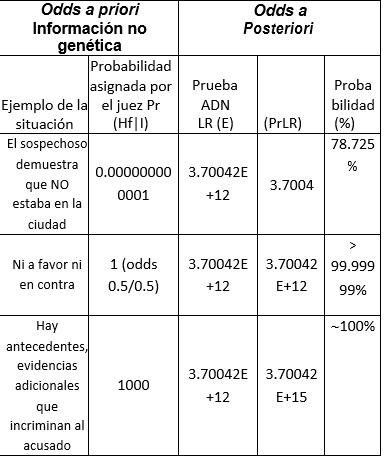
En el Cuadro 1 se aplica el teorema de Bayes usando el LR calculado (3.70042E+12), donde se plantean tres situaciones:
1) El juez no piensa que el sospechoso sea culpable por una información (I) no genética presentada, y le asigna un valor de 1 billón a favor del defensor Hd: Pr (Hf|I)= 0.000000000001, donde el símbolo “│” significa “dado que”. Se observa en el Cuadro 2 como el odds ratio, aunque a favor de Hf, ya no es poderosa.
2) El juez considera que no hay nada adicional relevante que evaluar, por lo que asigna la misma probabilidad para ambas hipótesis (Hf/Hd= 0.5/0.5 = 1); el odds posteriori es el mismo que el LR o evidencia genética (E).
3) El juez le asigna un valor de 1000 a favor de Hf por ciertos antecedentes del caso, lo cual aumenta proporcionalmente el odds final. Si se prefiere describir el odds posteriori como probabilidad o porcentaje se usa esta fórmula: Pr (Hf|E, I) = [LR x Pr (Hf|I)] / {LR x Pr (Hf|I) + [1- Pr (Hf|I)]}, la cual fue aplicada al ejemplo y presentada en la columna izquierda del Cuadro 2.
Cuando no existe base de datos poblacional del lugar donde sucedió el crimen y/o a la cual pertenece el acusado y se aplica la de una población diferente, la frecuencia de genética de los marcadores podría ser más baja que la población a la que realmente pertenece el acusado, con lo que se sobrevalora la evidencia y se perjudicaría al acusado.
Aplicación del Teorema de Bayes para integrar la evidencia genética (LR) a la probabilidad inicial para obtener la probabilidad final.
Esto contradice las recomendaciones del NRC (National Research Council, USA) de ser “conservativo”, es decir, tratar de que la interpretación favorezca al acusado, que deriva del dicho "más vale mil culpables libres, que un inocente en la cárcel"...
En Honduras, esta situación podría surgir en casos donde el inculpado es originario de algún grupo cerrado como algunos grupos de origen africano, judíos o indígenas) donde se espera un incremento de homocigosidad por subestructura poblacional. Cuando no se dispone de la base de datos adecuada para interpretar el perfil genético, el NRC recomienda usar la de la población general (hondureña), pero aplicar un factor de corrección (Θ, theta) al estimar la frecuencia de genotipos del perfil de ADN. Se recomiendan valores de Θ = 0.01 y 0.03 en grupos indígenas dependería de que tan cerrado sea el grupo del que es originario el inculpado. Para homocigotos, la p2 se convierte en: p2 + p (1-p) Θ, mientras para heterocigotos 2pq se convierte en 2pq (1- Θ). Por ejemplo, para TPOX la frecuencia de un homocigoto 8/8 sería p2= (0.427)2 = 0.18233; aplicando Θ= 0.01 a la corrección: 0.18233 + (0.427*0.573*0.01) = 0.18477. Por su parte, un heterocigoto 8/11 sería 2pq= 2* 0.427*0.213= 0.1819; aplicando Θ= 0.01 al factor de corrección se convierte en 0.180087.
Cabe mencionar que, con la potencia que ofrecen los kits más recientes (>20 STRs), la conclusión que involucra o no al sospechoso no cambiaría, ya sea usando la base de datos de población adecuada, una no tan adecuada, y aplicando (o no) el factor de corrección del NRC. Bajo esta perspectiva, en algunos países con mayor subestructura como los grupos raciales de Estados Unidos (EUA), genetistas forenses suelen ofrecen su dictamen aplicando diferentes bases de datos disponibles (p. ejem. caucásico, hispano, africano y asiático-americano). Con lo anterior se pueden evitar cuestionamientos de la defensa, y será decisión del juez decidir qué valor de LR tomar en cuenta, aunque finalmente todos llevarían a la misma conclusión. Lo que si sería cuestionable es no hacer la interpretación estadística, ya que un abogado informado tendría elementos para -incluso- hacer inadmisible la evidencia genética presentada en un dictamen. En breve, la sugerencia es hacerlo siempre.
Con la batería de 20 STRs de los kits tradicionales, la mayoría de las veces se obtienen valores LR o PCA suficientemente potentes para involucrar a cualquier sospechoso con la escena del crimen “más allá de la duda razonable”. Sin embargo, es necesario enfatizar que los genetistas forenses siempre describen el vínculo entre el sospechoso y la escena del crimen por la evidencia biológica analizada, en ningún caso hablan de culpabilidad9, eso es parte de la responsabilidad del juez dictaminarlo en un juzgado. Un aspecto interesante sobre la población de referencia proviene de un caso donde el abogado defensor logró invalidar la prueba de ADN por no existir una base de datos acorde a la herencia del acusado. El inculpado, provenía de abuelos paternos italianos, abuelo materno indígena americano, abuela materna mitad francesa- indígena. La defensa logró hacer inadmisible la prueba de ADN. Sin embargo, si se analiza la razón de verosimilitud (LR= Hf/Hd), vemos las frecuencias alélicas de la base de datos que se usan para valorar la hipótesis de la defensa (Hd), donde se asume que él inculpado no está vinculado con la evidencia sino algún otro individuo tomado al azar de la población. De manera que los orígenes del inculpado son irrelevantes para valorar la Hd, por lo que no se debió haber invalidado dicha prueba, al menos por esos argumentos.
CITAR COMO: Villalobos-Rangel H. Las pruebas de ADN en el contexto forense parte II.
Interpretación estadística. Rev. cienc. forenses Honduras. 2018; 4(2):17-22.
http://www.bvs.hn/RCFH/pdf/2018/pdf/RCFH4-2-2018-6.pdf (pdf)
https://www.lamjol.info/index.php/RCFH/article/view/8716 (html)
Secretaría del Grupo de Habla Española y Portuguesa de la Sociedad Internacional de Genética Forense
Delegado por México ante la Sociedad Latinoamericana de Genética Forense
hrangel13@hotmail.com

Representación del proceso de evaluación estadística de un caso criminal, donde se compara el perfil genético de la evidencia con el del sospechoso, que en el ejemplo coinciden (iguales).
Probabilidad de coincidencia al azar (PCA)= 32x10-8=0,0000000132 Likehood ratio (LR) = 1/1,32x10-8= 75,757,575
Evaluación estadística de un perfil genético X de 15 STRs asumiendo el equilibrio Hardy- Weinberg (EHW), las frecuencias alélicas y la regla del producto para obtener la probabilidad de coincidencia al azar (PCA) y el LR, aplicable a un caso criminal.
Aplicación del Teorema de Bayes para integrar la evidencia genética (LR) a la probabilidad inicial para obtener la probabilidad final.

Esto contradice las recomendaciones del NRC (National Research Council, USA) de ser “conservativo”, es decir, tratar de que la interpretación favorezca al acusado, que deriva del dicho "más vale mil culpables libres, que un inocente en la cárcel"...


