



PROBLEMA DE CAUCHY ASOCIADO A LA ECUACIÓN KdV SOBRE ESPACIOS DE SOBOLEV CON PESO
CAUCHY PROBLEM FOR KdV EQUATION IN WEIGHTED SOBOLEV SPACES
PROBLEMA DE CAUCHY ASOCIADO A LA ECUACIÓN KdV SOBRE ESPACIOS DE SOBOLEV CON PESO
Revista de la Facultad de Ciencias, vol. 8, núm. 2, 2019
Universidad Nacional de Colombia
Recepción: 10 Septiembre 2018
Aprobación: 04 Marzo 2019
Resumen:
En este trabajo se aborda, de una forma alternativa a las ideas sugeridas por Fonseca, Linares y Ponce en (Fonseca, G. et al., 2015), el buen planteamiento local del problema de Cauchy asociado a la ecuación Korteweg-de Vries
Con base en la fórmula de Duhamel y utilizando el teorema de punto fijo de Banach se demuestra la existencia y unicidad de solución en un subconjunto del espacio de Sobolev con peso Zs,r := Hs(R)∩L2(|x|rdx). Para esta finalidad se emplean estimativas lineales sobre el semigrupo unitario asociado y su derivada de Stein, argumentos similares a las ideas de Kenig, Ponce y Vega y un lema de interpolación de Nahas y Ponce. La dependencia continua del dato unicial u0 se deriva directamente del método empleado.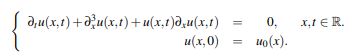
Palabras clave: Problema de Cauchy, KdV, Espacios de Sobolev con peso.
Abstract:
In this work we will face, in an alternative way to the ideas suggested by Fonseca, Linares and Ponce in (Fonseca, G. et al., 2015), the local well-posedness of the Cauchy problem associated to the Korteweg-de Vries equation
Based in the Duhamel’s formula and using the Banach fixed point theorem we are going to show the existence and uniqueness of solution in a subset of the weighted Sobolev space Zs,r := Hs(R)∩L2(|x|rdx). To this end, we will use linear estimates over the unitary semigroup and it’s Stein derivative; arguments based on Kenig, Ponce y Vega’s ideas and an interpolation lemma due to Nahas and Ponce. The continuous dependence on the initial data is obtained directly from the used method.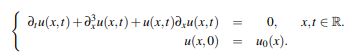
Keywords: Cauchy problem, KdV, weighted Sobolev spaces.
1. INTRODUCCIÓN
En este trabajo se va a estudiar el problema de valor inicial (PVI)
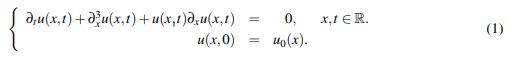 (1)
(1)La ecuación (1) fue derivada por Korteweg y de Vries en Korteweg, D. J. & de Vries, G. (1895) como un modelo que describe la propagación de ondas de longitud (de onda) larga en medios dispersivos y en una dimensión. La propagación de ondas solitarias en la superficie del agua en canales de poca profundidad es un ejemplo de contextos en los que aparece esta ecuación. En adelante se referirá a la ecuación (1) como ecuación KdV.
Desde el punto de vista matemático la ecuación KdV es una ecuación de evolución en derivadas parciales que incluye efectos de dispersión y no linealidad. El término ∂tu(x,t) se puede entender como la evolución temporal de la perturbación u(x,t) mientras que ∂3u(x,t) se traduce en la dispersión del sistema. El término restante u(x,t)∂xu(x,t) es de carácter no lineal
En la literatura la ecuación KdV ha sido ampliamente estudiada (Colliander, J. et al., 2003; Kato, T., 1983; Kenig, C. & Vega, L., 1993; Miura, R., 1976). La descripción de diversos problemas físicos y matemáticos asociados a esta ecuación, que abarcan desde aspectos geométricos y algebraicos hasta cuestiones propias del análisis no lineal, puede ser consultada en Miura, R. (1976). Los esfuerzos serán direccionados a establecer el buen planteamiento local del problema de Cauchy (1).
Durante las últimas décadas el buen planteamiento del problema (1) ha sido objeto de estudio por varios autores, ver por ejemplo (Bourgain, J., 1993; Colliander, J. et al., 2003; Kato, T., 1983; Kenig, C. & Vega, L., 1993) y las referencias allí citadas. Dichos autores estudiaron el problema en los espacios de Sobolev Hs(R). Dado que el índice s en la definición de Hs(R) mide el grado de diferenciabilidad de una función en L2(R), tales espacios son un contexto funcional natural para estudiar el PVI (1). Recientemente se ha incrementado el interés por estudiar el buen planteamiento del problema de Cauchy en espacios que no solo midan el grado de diferenciabilidad de las funciones sino también el tipo de decaimiento que las soluciones del problema puedan tener ((Bustamante, E. et al., 2013), (Bustamante, E. et al., 2018), (Fonseca, G. & Ponce, G. , 2011); entre otras). Tal estudio viene motivado por la existencia de soluciones especiales (ondas solitarias) que tienen un decaimiento particular y por el estudio de la persistencia de soluciones para las cuales el dato inicial u0 pertenezca al espacio de Schwartz S(R) (Kato, T., 1983) tiene un abordaje ilustrativo).
El trabajo pionero en esta dirección es debido a Tosio Kato. Con el objetivo de estudiar las soluciones del PVI (1) con dato inicial u0 ∈S(R), Kato propone abordar el problema del buen planteamiento en los espacios de Sobolev con peso Hm(R)∩L2(|x|ndx), donde n y m son enteros positivos Kato, T. (1983). Los resultados de este trabajo han sido extendidos para los casos en que m y n no son necesariamente enteros positivos y para otros modelos dispersivos no lineales como las ecuaciones Benjamin-Ono o Zakharov-Kuznetsov (ver por ejemplo Bustamante, E. et al. (2013), Fonseca, G. et al. (2015), Fonseca, G. & Ponce, G. (2011), Nahas, J. & Ponce, G. (2009) y sus referencias).
A diferencia de otras ecuaciones dispersivas, el efecto de dispersión de la ecuación KdV es significativo y permite estudiarse a la luz de los teoremas de punto fijo. Existen ecuaciones en las que la dispersión es más leve, lo cual exige que la conclusión de buen planteamiento deba ser obtenida con herramientas adicionales. Por ejemplo en Molinet, L. et al. (2001) se demuestra que la función dato-solución de la ecuación de Benjamin-Ono no es localmente C2. Más aún, Koch, H. & Tzvekov, N. (2005) garantiza que la misma no es localmente uniformemente continua.
En contraste con las ideas desarrolladas en Colliander, J. et al. (2003), las herramientas principales que serán usadas en este artículo recaen indirectamente sobre la transformada de Fourier (ver Teorema 2.2).
El objetivo entonces es extender el Teorema 2.1 en Kenig, C. & Vega, L. (1993) para demostrar en una forma alternativa a las ideas presentadas en (Fonseca, G. et al., 2015), el buen planteamiento local del problema de Cauchy asociado a la ecuación KdV en los espacios de Sobolev con peso Hs(R)∩L2(|x|rdx).
En Fonseca, G. et al. (2015) los autores demuestran en el Teorema 2 que el problema de Cauchy para la ecuación KdV modificada
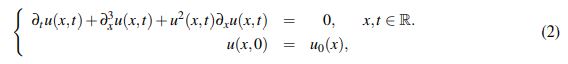 (2)
(2) está bien planteado en los espacios de Sobolev con peso. Los autores sugieren que las ideas pueden replicarse para concluir el buen planteamiento de la familia de ecuaciones
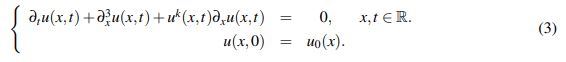 (3)
(3) donde k es un entero positivo.
A diferencia de lo desarrollado por ellos, en estre trabajo se utilizan estimativas alternativas que no recaen directamente en el uso exhaustivo de la transformada de Fourier (compare Lema 1 de Fonseca, G. et al. (2015) con los lemas 2.4 y 2.5) e ideas de interpolación como las desarrolladas en la demostración del teorema 2.4 de Bustamante, E. et al. (2013) para demostrar que el PVI (1) (caso k=1) está bien planteado sobre los espacios de Sobolev con peso mencionados anteriormente.
Con base en la fórmula de Duhamel (ver la sección 5 del capítulo IX en Kato, T. (2013)) se va a entender como una solución al PVI (1) una función u que satisfaga
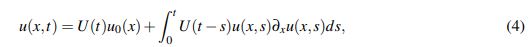 (4)
(4)donde la familia de operadores {U(t)}t≥0 es el semigrupo unitario asociado a las soluciones al problema (1) linealizado. De forma que, teniendo en cuenta la expresión (4), una buena forma de afrontar el problema (1) es intentar que el operador que define el lado derecho de (4) sea una contracción en algún espacio métrico razonable. En otras palabras demostrar que el operado
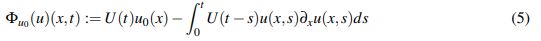 (5)
(5)tiene un único punto fijo en cierto espacio Y.
Esta idea fue implementada en Kenig, C. & Vega, L. (1993) por Kenig, Ponce y Vega en los espacios de Sobolev Hs(R), con s > 3/4; donde usando el teorema de punto fijo de Banach, estos autores obtuvieron el buen planteamiento local del problema de valor inicial (1) sobre un subconjunto de Hs(R). Dado que el objetivo de este artículo adicionalmente involucra el estudio del decaimiento de las soluciones del PVI (1), observando (4) y (5) se puede notar que va a ser necesario controlar expresiones del tipo
 (6)
(6)
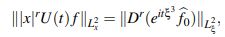
donde Dr(f) se define por (|x|r f^)∨ . Es decir, en lugar de estimar la norma de U(t)f en L2(|x|rdx) se puede estimar la norma de Dr(eitξ 3 f^0) en L2(R).
Con el objetivo de estimar la norma L2 del término Dr(eitξ3 f^0), se usa una versión alternativa a la derivada fraccionaria usual, que se denotará por Dr . Este operador fue introducido por Stein en Stein, E. (1961) con la finalidad de caracterizar los espacios de Sobolev generalizados Lpb(Rn). Haciendo uso de esta caracterización, se va a estimar el término ||Dr(eitξ3 f^)||L2/ξ vía estimativos sobre la expresión ||Dr(eitξ3 f^)||L2/ξ. A su vez, este mismo es acotado en términos de ||f||L2x , ||D2rf||L2x y de |||x|rf||L2x.
De tal manera que, tanto los estimativos lineales sobre el semigrupo U(t) obtenidos por Kenig, Ponce y Vega y el acotamiento de |||x|rU(t)f ||L2x, permiten escoger un espacio de Banach adecuado en el cual se pueda encontrar soluciones para el problema (1) por medio del teorema de punto fijo de Banach.
Este artículo está organizado de la siguiente manera: en la sección 2 la teoría lineal relacionada al problema. La solución del problema linealizado, la definición del semigrupo unitario asociado, estimativas sobre la derivada de Stein del semigrupo, los estimativos lineales de Kenig, Ponce y Vega junto con algunos lemas de interpolación serán abordados. Al inicio de la sección 3 se explica la relación entre los índices de regularidad y decaimiento s y r enunciados en el teorema principal. La demostración de este teorema será presentada en dos pasos: inicialmente se recuerda la existencia y unicidad de soluciones locales para el problema (1) en Hs(R) obtenidas en (Kenig, C. & Vega, L., 1993). El segundo paso involucra el decaimiento de las soluciones y será dividido en dos subcasos; cuando 3/4 < s ≤ 1, con base en los estimativos lineales, se usará el método de punto fijo de Banach y cuando s > 1, usando la propiedad de regularidad de Kenig, Ponce y Vega junto con los lemas de interpolación, se demostrará que la solución que se tenía en Hs(R) también pertenece al espacio L2(|x|rdx).
2. TEORÍA LINEAL PARA LA ECUACIÓN KORTEWEG-DE VRIES
Es importante resaltar que para esta sección y las siguientes la constante C será usada para representar cantidades escalares que pueden variar línea a línea y cuya dependencia será siempre especificada.
2.1. Solución del problema de valor inicial lineal asociado
Considere el problema lineal homogéneo asociado a (1)
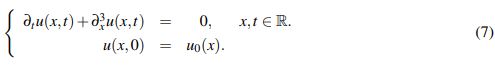 (7)
(7)Vía transformada de Fourier se puede ver que la solución a (7) está dada por el operador U : [0,∞) → C1(R;R) definido por
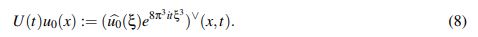 (8)
(8)Este operador es llamado el grupo unitario asociado a la ecuación KdV linealizada y la familia {U(t)}t≥0 define un semigrupo de operadores lineales. La parte constante en el exponente, 8π3, será omitida frecuentemente cuando se invoque U(t). La razón de tal simplificación es que, en adelante, el término 8π3 solo aportará constantes en las estimativas y por lo tanto lo que se demuestre para el exponente itξ3 será válido tambien para el exponente 8π3itξ3, a menos que se especifique lo contrario.
2.2. Derivada de Stein
Para una función con las propiedades adecuadas (por ejemplo una de la clase de Schwartz) y b > 0 se definen los siguientes operadores:
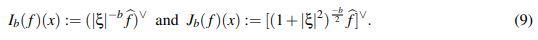 (9)
(9)Definición 2.1. Denote por Lbp(Rn) el conjunto {f = Jb(g) | g ∈ Lp(R)}.
Note que en el caso p = 2, el espacio Lbp(Rn) coincide con el espacio de Sobolev Hb(Rn).
Una caracterización simple de los elementos de Lbp(Rn) en términos de su suavidad sin utilizar la transformada de Fourier queda condensada en el próximo teorema extraido de (Stein, E., 1961).
Teorema 2.2 (Stein). Sean b ∈ (0,1) y 2n/(n+2b) < p < ∞. Una función f pertenece a Lp b (R n ) si, y solo si,
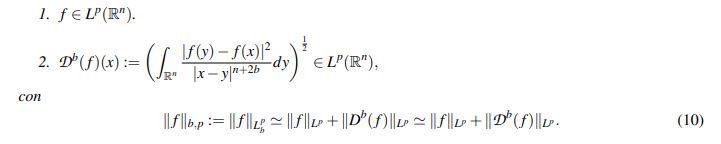 (10)
(10)La expresión Dbf definida en el numeral 2 del Teorema 2.2 se conoce como Derivada de Stein y tiene varias ventajas con respecto a la derivada fracionaria clásica
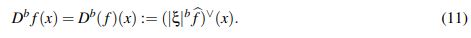 (11)
(11)Un ejemplo de la afirmación anterior es que no se conoce aún si se puede o no obtener una regla del producto, similar al Teorema 2.3 (abajo), pero con Db en lugar de Db. Ver la Proposición 1 de (Nahas, J. & Ponce, G., 2009).
Teorema 2.3 ( (Nahas, J. & Ponce, G., 2009)). Sean b ∈ (0,1) y 1 ≤ p ≤ ∞. Si f,g : Rn → C son funciones medibles, entonces
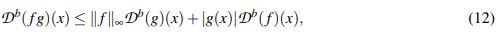 (12)
(12)
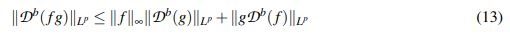 (13)
(13)
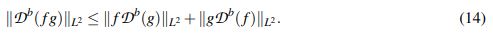 (14)
(14)2.3. Estimativos sobre el Semigrupo
Se comienza la sección con el Lema 2.4 que es debido a Bustamante, Jiménez y Mejía (ver Lema 2.2 en Bustamante, E. et al. (2018)). Este lema permite acotar la derivada de Stein del multiplicador que aparece en la definición del semigrupo unitario asociado a la ecuación KdV linealizada en términos de potencias de t y |x|.
Lema 2.4. Sea b ∈ (0,1). Existe una constante Cb > 0 tal que para todo t > 0 y todo x ∈ R se tiene que
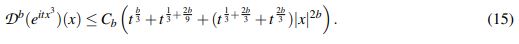 (15)
(15)El siguiente lema se encarga de acotar |||x|bU(t)u||Lx2 en términos de ||u||Lx2, ||D2bu||Lx2 y |||x|bu||Lx2 junto con sumas de potencias de t; permitiendo incluir el decaimiento en el espacio de Banach donde más adelante se definirá una contracción en la búsqueda de obtener (4). La prueba de este hecho se sigue de una pequeña adaptación de la prueba del Lema 2.4 en Bustamante, E. et al. (2018).
Lema 2.5. Para b ∈ (0, 1 2 ] existe una constante Cb > 0 tal que para todo t ≥ 0 y para toda f ∈ Z2b,b := H2b (R)∩L2 (|x|2bdx) se tiene que
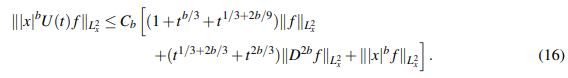 (16)
(16)Definición 2.6. Dada una función f : R×[0,T] → R (o C) se define la norma mixta
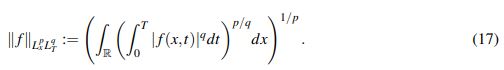 (17)
(17)Cuando p =∞ o q =∞ se deben hacer los cambios naturales con essup. Adicionalmente cuando en la norma aparezca t en lugar de T, se entenderá que el intervalo de tiempo es [0,∞).
El espacio formado por las funciones con norma mixta finita es llamado espacio anisotrópico o espacio de Bochner uniforme. Estos conceptos fueron introducidos por Benedek & Panzone (1961) y fueron investigados a profundidad por Besov et al. (1979).
Teorema 2.7 (Estimativos lineales).
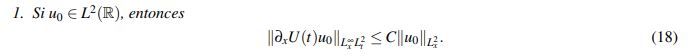 (18)
(18)
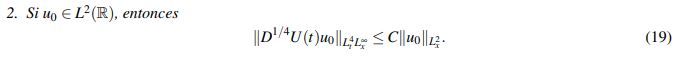 (19)
(19)
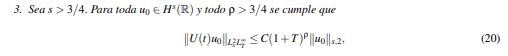 (20)
(20)Para las justificaciones de cada literal se le sugiere al lector revisar en Kenig, C. & Vega, L. (1993) el Teorema 3.5, parte (i); el Lema 3.18 parte (i) y el Lema 3.19 respectivamente.
El siguiente teorema es una aproximación cercana a la regla de Leibniz (en una versión vectorial) para derivadas fracionarias. La prueba de este resultado puede consultarse en el Apéndice A8 de Kenig, C. & Vega, L. (1993).
Teorema 2.8. Sea α ∈ (0,1). Considere α1,α2 ∈ [0,α] tales que α = α1 +α2. Sean |/p, p1, p2,q,q1,q2 ∈
Teorema 2.8. Sea α ∈ (0,1). Considere α1,α2 ∈ [0,α] tales que α = α1 + α2. Sean p, p1, p2,q,q1,q2 ∈ (1,∞) tales que 1/p = 1/p1 + 1/p2 y 1/q = 1/q1 + 1/q2 . Entonces
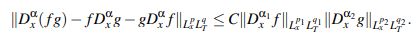
Más aún, para α1 = 0 el valor q1 = ∞ también es válido.
Se concluye este capítulo incluyendo dos resultados: un lema de interpolación debido a Germán Fonseca y Gustavo Ponce (Lema 1 en (Fonseca, G. & Ponce, G. , 2011)) y una consecuencia de la regla de Leibniz encontrada en Bustamante, E. et al. (2013) que nos permitirán aclarar en primera instancia la relación entre la regularidad y el decaimiento de las funciones en los espacios intermedios en el sentido expuesto a continuación.
Lema 2.9 (Fonseca-Ponce). Sean a > 1 y b > 0. Suponga que Jaf ∈ L2(R) y que p(x)bf :=(1+|x|2)b/2f ∈ L2(R). Entonces para todo θ ∈ [0,1] :
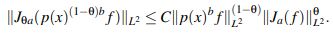
Más aún, la desigualdad sigue siendo válida para el peso truncado
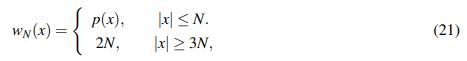 (21)
(21)en lugar de p(x) y con la constante C independiente de N.
La demostración del siguiente lema se sigue de aplicar inducción y la regla de Leibniz (ver Lema 2.2 en Bustamante, E. et al. (2013)).
Lema 2.10. Sean b > 0 y n ∈ N. Suponga que Jn(p(x)bu0) ∈ L2(R). Entonces
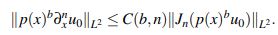
Más aún, el resultado sigue siendo válido para wN(x) en lugar de p(x) y con la constante independiente de N.
3. TEOREMA PRINCIPAL
En esta sección se presenta el resultado principal de este trabajo. Se prueba la existencia de soluciones para el PVI asociado a la ecuación KdV cuando el dato inicial pertenece a cierto espacio de Sobolev con peso. Antes de presentar la prueba de dicho resultado se discuten algunos aspectos relacionados con el método para encontrar soluciones para el PVI (1) y se motiva la escogencia del espacio de Sobolev con peso en el cual se estudia este problema.
3.1. Formulación del problema
Una buena manera de encontrarle una solución al problema de valor inicial de la ecuación Korteweg-de Vries
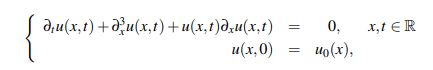
es usar el teorema de punto fijo de Banach junto con la fórmula de Duhamel. En otras palabras se llama solución del problema (1) a una función u ∈ C([0,T];Z), para cierto espacio de Banach Z, que satisfaga la expresión integral
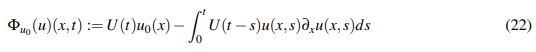 (22)
(22)sea una contracción.
La búsqueda de tal espacio de Banach Z adecuado para esta labor depende directamente de los estimativos lineales (Teorema 2.7) disponibles para el semigrupo asociado.
Como el interés es establecer la buena colocación para el problema de Cauchy en espacios de Sobolev con peso Zs,r := Hs(R)∩L2(|x|rdx) es necesario saber la relación (si existiera) entre los índices s y r; es decir, entre el decaimiento y la regularidad de la posible solución. La respuesta en el contexto presentado será r = s/2 y se motiva de los siguientes razonamientos formales basados en las ideas de Tosio Kato en Kato, T. (1983).
Suponga que se tiene una solución para (1), u ∈ C([0,∞);Hs
(R)), para algún s suficientemente grande. Se
desea garantizar que la cantidad 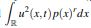 sea finita y acotada en t, donde p(x) := (1 + |x|2
)1/2
.
Procediendo formalmente, se multiplica la ecuación KdV a ambos lados por u(x,t)p(x) y se usa integración
por partes para obtener:
sea finita y acotada en t, donde p(x) := (1 + |x|2
)1/2
.
Procediendo formalmente, se multiplica la ecuación KdV a ambos lados por u(x,t)p(x) y se usa integración
por partes para obtener:
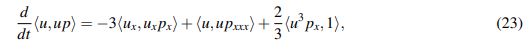 (23)
(23)donde <·,·> es el producto interno en L2(R).
Los dos términos que aparecen sumando al lado derecho de la expresión (23) pueden controlarse fácilmente como se mostrará en (49) y (51). El término restante es un poco más delicado. El Lema 2.9 afirma que para θ ∈ [0,1] y f ∈ Zs,r,
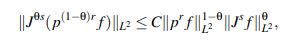
es decir, en términos de u:
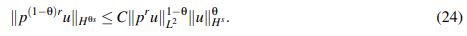 (24)
(24)Para controlar la expresión 3<ux,uxpx> se puede utilizar (24) cuando θs = 1 pero requiriendo entonces que |px| sea del orden de p2(1−θ)r. Dado que |px| ≤ p2r−1, la igualdad 2r −1 = 2(1−θ)r lleva a concluir que r = s/2.
Tal y como se mencionó en la introducción, el estudio del buen planteamiento de (1) en los espacios de Sobolev clásicos Hs(R) fue desarrollado por Kenig, Ponce y Vega en Kenig, C. & Vega, L. (1993). Más precisamente en el Teorema 2.1, se afirma lo siguiente:
Teorema 3.1 (Kenig-Ponce-Vega). Sea s > 3/4. Para toda u0 ∈ Hs(R) existe T > 0, que depende solo de ||u0||s,2, y una única solución u(t) del PVI (1) que satisface
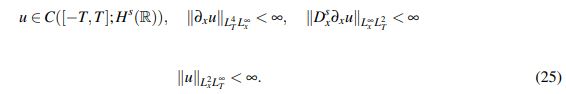 (25)
(25)Para cualquier T0 ∈ (0,T) existe una vecindad V de u0 en Hs(R) tal que el mapeo u˜0 → u˜(t) desde V hacia el espacio definido por (25), con T' en lugar de T, es Lipschitz.
Si u0 ∈ Hs'(R), con s' > s, entonces los resultados mencionados arriba se mantienen con s' en lugar de s y en el mismo intervalo de tiempo [−T,T].
Teniendo en cuenta que la relación de s y r es r = s/2 y el Teorema 3.1 se puede enunciar el resultado principal de este artículo.
Teorema 3.2 (Teorema Principal). Sea s > 3/4. Para toda u0 ∈ Zs, x/2 := Hs (R)∩L2 (|x|s/2dx) existe T > 0 (que depende sólo de ||u0||s,2 si s > 1 y también de |||x|s/2u0||L2 si 3/4 < s ≤ 1) y una única solución u(t) del problema (1) que satisface
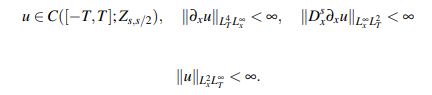
Se presenta la prueba en dos pasos.
3.2. Demostración del Teorema Principal
Paso1
Este paso recapitula la demostración del Teorema 2.1 en Kenig, C. & Vega, L. (1993).
Para todo T > 0, toda w ∈C([−T,T];Hs(R)) y todo ρ > 3/4, se define

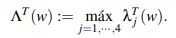
Se puede probar que dado u0 ∈ Hs(R), si se toma T > 0 y a > 0 tales que
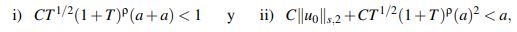
se tiene que para u,v ∈ XaT := {w ∈C([−T,T];Hs(R)) | ΛT(w) ≤ a} se cumple que
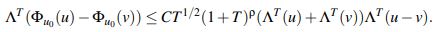
lo cual probaría el teorema la existencia y unicidad de solución sobre los espacios Hs(R).
Paso2
Caso 1, si 3/4 < s ≤ 1.
Para todo T > 0, toda función w ∈C([−T,T];Zs,s/2) y s > 3/4, se define
 (26)
(26)Se trabaja de nuevo en un espacio semejante a XaT, en este caso
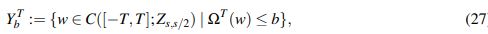 (27)
(27)para algún b > 0 que se define más adelante.
Se comienza estimando ΩT(U(t)u0).
En primer lugar se observa que
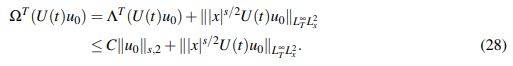 (28)
(28)En virtud del Lema 2.5 se tiene
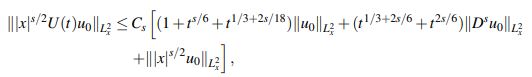
y así
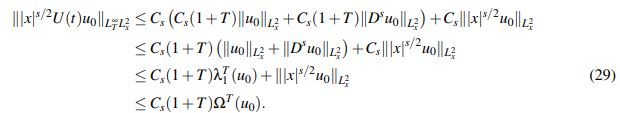 (29)
(29)De lo anterior y (28) se tiene que
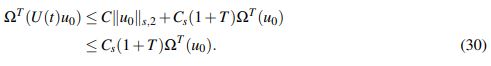 (30)
(30)Defina ahora Ψu0 : YTb → YTb . Para u ∈ YTb dado, se estima ΩT (Ψu0 (u)).
En primer lugar note que del paso 1,
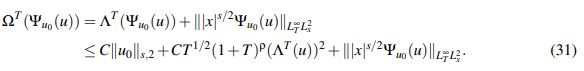 (31)
(31)En segundo lugar es claro que para t ∈ (0,T) se tiene
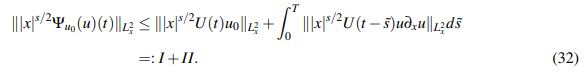 (32)
(32)Argumentando con base en el Lema 2.5 se obtiene para I:
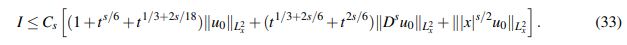 (33)
(33)De otro lado, escribiendo t∗ := t −s˜ e invocando el Lema 2.5 junto con la desigualdad de Hölder, se tiene para II que
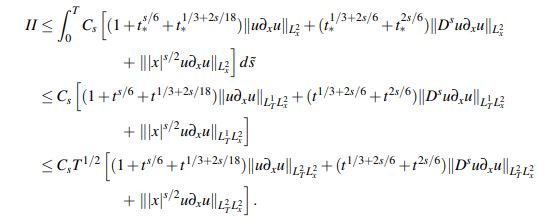
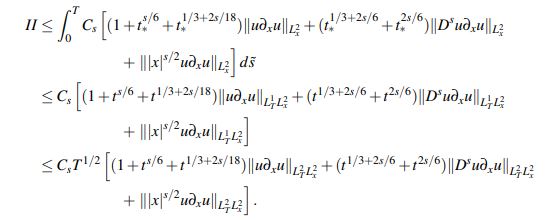
Utilizando que
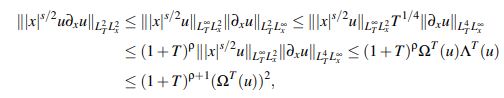
se puede continuar el acotamiento de II como
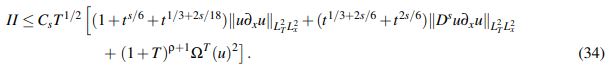 (34)
(34)Combinando (32), (33) y (34) se concluye que
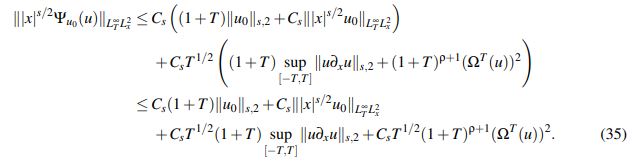 (35)
(35)Finalmente, por (35) se tiene que
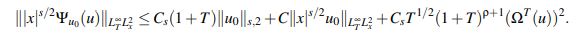
Regresando a (31) se ha probado que
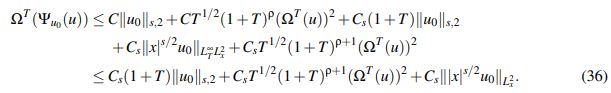 (36)
(36)El estimativo (36) da la primera condición sobre b y T para seleccionarlos de manera tal que la función Ψu0 esté bien definida. Se debe ahora intentar establecer una condición razonable para obtener que Ψu0 sea una contracción.
Inicialmente se acota ΩT(Ψu0(u)−Ψu0(v)). Para u,v ∈YbT, se tiene que
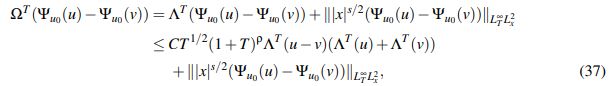 (37)
(37)donde se usa que para u,v ∈ XaT se tiene
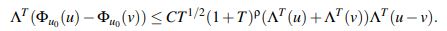
Se verá que para u,v ∈YbT se tiene que
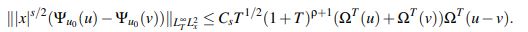
En efecto,
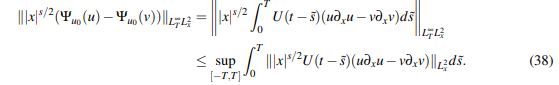 (38)
(38)Como consecuencia del Lema 2.5 y la desigualdad de Hölder:
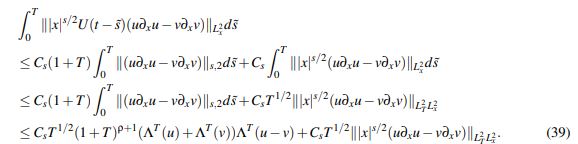 (39)
(39)Usando nuevamente la desigualdad de Hölder:
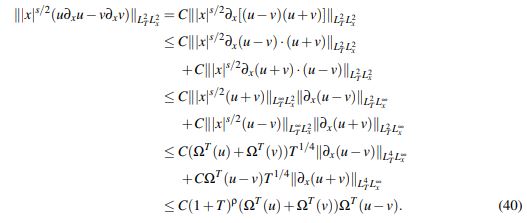 (40)
(40)Recopilando los estimativos (38), (39) y (40) se obtiene que
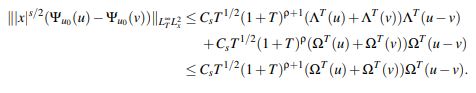
Combinando lo anterior y (37) se concluye que
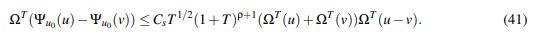 (41)
(41) En este punto lo único que queda restando es seleccionar T y b para que Ψu0 :YbT →YbT sea una contracción.
Para alcanzar esto se deben garantizar las siguientes dos condiciones:
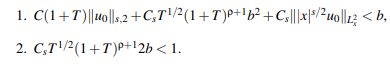
La condición 1, como se mencionaba antes, viene de (36) para garantizar la buena definición de Ψu0. La condición 2 aparece explícita en (41) para que Ψu0 sea una contracción.
Si se estudia la desigualdad para b se obtiene que T debe satisfacer
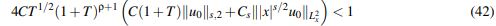 (42)
(42)para que pueda existir una solución.
Defina T > 0 por
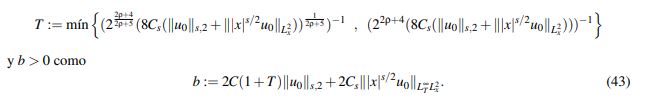 (43)
(43)Como el lector puede verificar, esta escogencia satisface las condiciones 1 y 2.
Aplicando entonces el Teorema de punto fijo de Banach, debe ser el caso que exista una única u ∈ YbT tal que Ψu0(u) = u.
Esto se concluye el caso 3/4 < s ≤ 1.
Caso 2, si s > 1.
Para este caso se aborda un procedimiento diferente al llevado a cabo anteriormente. Del Teorema 3.1, dado u0 ∈ Hs(R) existe T > 0 (dependiendo solamente de ||u0||s,2) y una única función u ∈ XaTque es solución del problema (1). Sea {u0m}m∈N una sucesión en C∞0 (R) tal que u0m −−m→∞−→ u0 en Hs(R). Sea um ∈ C([0,T];H∞(R)) la solución del problema (1) con dato inicial u0m dada por el Teorema 3.1. SE puede suponer que todas las um están definidas en el mismo intervalo [−T,T]. Adicionalmente por la dependencia continua del dato en el Teorema 3.1, um −m→∞−−→ u en C([0,T];Hs (R)).
En un espíritu similar al descrito en la motivación de la relación entre s y r desarrollado al inicio del capítulo, se multiplica la ecuación (1) para um por umw2rN , donde wN es el peso truncado definido en el Lema 2.9; para obtener:
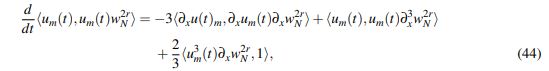 (44)
(44)donde <·,·> es el producto interno de L2(R). Integrando (44) en el intervalo temporal [0,t] y aplicando el teorema fundamental del cálculo se obtiene que
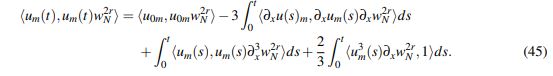 (45)
(45)Como tanto w2Nr y sus derivadas están acotadas con constante independiente de N, al tomar límite cuando m → ∞ en (45) se obtiene que
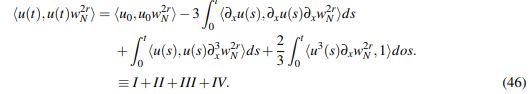 (46)
(46)Note que el lado izquierdo de (46) converge a la norma ||u||2L2((1+|x| 2) rdx) cuando N → ∞; de modo que si se logra dominarlo por algo finito independiente de N, se obtiene que u tiene el decaimiento deseado. Con este propósito se procede a estimar cada término. Para I, se tiene que
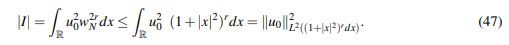 (47)
(47)En segundo lugar, usando el Lema 2.10 y el Lema 2.9 para a = s, b = r, θs = 1 y (1−θ)b = r −1/2 se tiene:
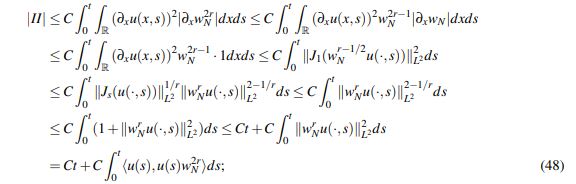 (48)
(48)donde luego de interpolar se usaa que u es continua de [0,T] en Hs(R) y que para cualquier caso ||wrNu(·,s)||2−1/rL2 ≤ (1+||wrN u(·,s)||2L2 ).
Para estimar III se deben considerar dos casos:
Si 2r−3 ≤ 0, entonces
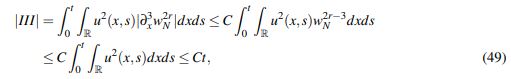 (49)
(49) donde se utilizó que las derivadas de wN(x) son acotadas y que u es continua de [0,T] en Hs(R).
Si 2r−3 > 0:
Si 2r−3 > 0: (49) Importar tabla
Nuevamente en virtud de que las derivadas de wN(x) son acotadas y de que w2rN(x)> w2r−iN (x) para i ∈ {1,2,3}; se tiene que
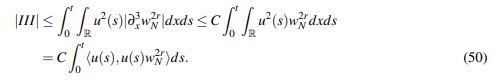 (50)
(50) Por último, para IV, usando la inmersión Hs(R) ,→ L∞(R):
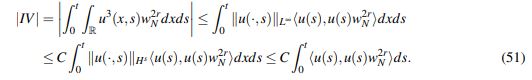 (51)
(51)De (46), (47), (48), (49), (50) y (51) se concluye que
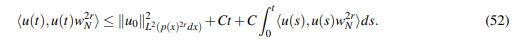 (52)
(52)En virtud de la desigualdad de Grönwall (lema 1.1 en Adedayo (2001)) y usando la notación Lw2 para
L2(p(x)2rdx):
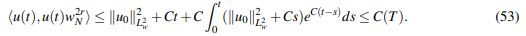 (53)
(53)Al tomar límite cuando N → ∞, se obtiene:
 (54)
(54)De lo anterior se concluye que u ∈ L∞([0,T];L2(p(x)2rdx)).
Por último nos resta por verificar que efectivamente u es continua de [0,T] en Zs,s/2. De (53) es claro que existe una constante positiva M tal que, para todo t ∈ [0,T],
 (55)
(55)Teniendo en cuenta que u ∈ C([0,T];L2(R)), dado ε > 0 arbitrario, para ε˜:= kε > 0 existe δ > 0 tal que si |t −s| < δ entonces ku(t)−u(s)kL2 < ε˜.
Tomando k = ||φ||−1L2w , es fácil ver que para φ ∈ L2(p(x)2rdx) la función t→<φ,u(t)>L2w es continua. En efecto, si |t −s| < δ:
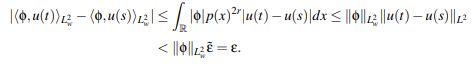
Se probará ahora que u : [0,T] → L2(p(x)2rdx) es continua en t = 0.
De (55) se tiene que
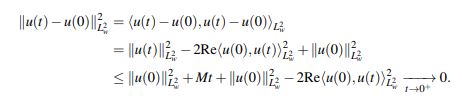
Por tanto, u : [0,T] → L2(p(x)2rdx) es continua en t = 0.
Para ver la continuidad en t0 ∈ [0,T] arbitrario basta mencionar que al ser v1(x,t):=u(x,t0 +t) y v2(x,t):=u(x,t0 −t) soluciones del problema (1), también son continuas en cero.
Finalmente se prueba que si ˜um ∈ C([0,T];Zs,s/2) es la solución de (1) correspondiente al dato inicial u˜0m, donde {u˜0m}m∈N forma una sucesión que converge a u0 en Zs,s/2 ; entonces ˜um converge a u en C([0,T];Zs,s/2).
Del Teorema 3.1 se tieen que ˜um −−m→∞−→ u enC([0,T];Hs(R)), por lo que sólo se debe probar que ˜um converge a u en L∞([0,T];L2(p(x)2rdx)).
Defina vm := u˜m−u y vm0:= u˜m0−u. Teniendo en cuenta que vm −−m→∞−→ 0 enC([0,T];Hs (R)) y argumentando de la misma forma en que se obtuvo que u ∈ L∞([0,T];L2 (p(x)2rdx)) se puede establecer que
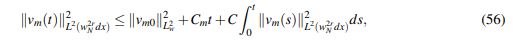 (56)
(56)La prueba del teorema queda completa.
Comentario 3.3. Del Teorema Principal 3.2 se puede garantizar la existencia y unicidad de la solución al problema (1) en el espacio de Sobolev con peso YTb definido en (27). El paso restante para establecer el buen planteamiento del problema de valor inicial asociado a la ecuación KdV se deriva directamente de la técnica empleada en la demostración anterior. Se debe justificar la continuidad de la función dato-solución desde Zs,s/2 hacia YTb . Para tal finalidad basta mostrar que esta función es continua en el sentido Lipschitz argumentando de la siguiente manera:
Para T' ∈ (0,T), sean u0 y v0 datos iniciales en Zs,s/2 con sus respectivas soluciones u y v dadas por el teorema principal. Siguiendo las ideas utilizadas para obtener (41) junto con las condiciones (42) y (43) se obtiene que
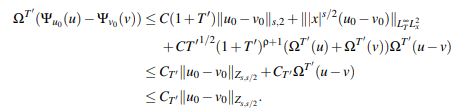
Referencias
Oguntuase, J. A. (2001). On an inequality of gronwall. Journal of inequalities in pure and applied math, 2(1).
Benedek, A. & Panzone, R. (1961). The space lp with mixed norm. Duke Math Journal, 28, 301–324.
Besov, O., Ilin, V., & Nikolskii, S. (1979). Integral respresentation of functions and inbedding theorems, vol 1, Scripta Series in Math.
Bourgain, J. (1993). Fourier transform restriction phenomena for certain lattice subsets and application to nonlinear evolution equations. ii. the kdv equation. Fourier transform restriction phenomena for certain lattice subsets and application to nonlinear evolution equations. II. The KdV equation, Geometric and Functional Analysis, 3(3), 209-262.
Bustamante, E., Jimíenez, J., & Mejía, J. (2013). Cauchy problems for the fifth order kdv equations in weighted sobolev spaces. arXiv preprint arXiv:1312.1552.
Bustamante, E., Urrea, J.J., & Mejia, J. (2018). A note on the Ostrovsky equation in weighted Sobolev spaces. Journal of Mathematical Analysis and Applications,, 460(2), 1004-1018.
Colliander, J., Keel, M., Staffilani, G., Takaoka, H., & Tao, T. (2003). Sharp global well-posedness for kdv and modified kdv on r and t. J. Amer. Math. Soc, 3, 705-749.
Fonseca, G., Linares, F., & Ponce, G. (2015). On persistence properties in fractional weighted spaces. Journal of the American Mathematical Society, 16(3) , 705-749.
Fonseca, G. & Ponce, G. (2011). The ivp for the benjamin-ono equation in weighted sobolev spaces. Journal of Functional Analysis, 260(2), 436-459.
Kato, T. (1983). On the cauchy problem for the (generalized) korteweg-de vries equation. Studies in Appl. Math. Adv. in Math. Suppl. Stud., 8(260), 93-128.
Kato, T. (2013). Perturbation theory for linear operators. Springer Science & Business Media.
Kenig, C., Ponce, G., & Vega, L. (1993). Well-posedness and scattering results for the generalized kortewegde vries equation via contraction principle. Communications on Pure and Applied Mathematics, 46(4), 527-620.
Koch, H. & Tzvekov, N. (2005). Nonlinear wave interactions for the benjamin-ono equation. Internationa lMathematics Research Notices, 2005(30), 1833-1847.
Korteweg, D. J. & de Vries, G. (1895). XLI. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 39(240), 422-443.
Miura, R. (1976). The Korteweg de Vries equation: A survey of results. SIAM review, 18(3), 412-459.
Molinet, L., Saut, J. C., & Tzvetkov, N. (2001). III-posedness issues for the benjamin-ono equation. SIAM journal on mathematical analysis, 33(4), 982-988.
Nahas, J. & Ponce, G. (2009). On the persistent properties of solutions to semi-linear schrodinger equation. Communications in Partial Differential Equations, 34(10), 1208-1227.
Stein, E. (1961). Characterization of function arising as potentials. Bulletin American Mathematical Society, 67.

