



LOS RESIDUALES RQR: UNA MEDIDA DIAGNÓSTICA EN R PARA LOS MODELOS CUB
LOS RESIDUALES RQR: UNA MEDIDA DIAGNÓSTICA EN R PARA LOS MODELOS CUB
Revista de la Facultad de Ciencias, vol. 9, núm. 1, 2020
Universidad Nacional de Colombia
Recepción: 06 Mayo 2019
Aprobación: 13 Noviembre 2019
Resumen: Cuando una persona califica un producto o servicio usualmente lo hace en una escala numérica de 1 a m. Se han propuesto varias metodologías estadísticas para su análisis; una de ellas son los modelos CUB. Sin embargo, para este tipo de modelos no existe una herramienta para verificar la calidad global del ajuste del modelo. En este artículo se proponen los residuales RQR que sirven como medida diagnóstica del modelo ajustado. La utilidad de los RQR se ilustra por medio de ejemplos usando datos simulados y datos reales. La nueva propuesta de residuales RQR se implementó en el paquete cubm de R y permite que cualquier usuario los pueda utilizar de una manera sencilla sin tener que programar.
Palabras clave: Modelos CUB, Datos ordinales, Medida de ajuste, Residuales RQR, R.
Abstract: When a person qualifies a product or service they usually do it on a numerical scale of 1 to m. Several statistical methodologies have been proposed for analysis; One of them are CUB models. However, for this type of model there is no tool to verify the overall quality of the model fit. This article proposes the RQR residuals that serve as a diagnostic measure of the fitted model. The utility of the RQR is illustrated by means of examples using simulated data and real data. The new proposal of RQR residuals is implemented in the cubm package of R and allows any user to use them in a simple way without having to program
Keywords: CUB models, Ordinal data, Fitting measure, RQR residuals, R.
1. INTRODUCCIÓN
Para el análisis de las variables de tipo ordinal como la satisfacción o la calidad, se han empleado técnicas estadísticas que permiten modelar una variable dependiente discreta, en función de una o varias variables predictoras. Algunas de estas técnicas son: los modelos de regresión (McCullagh, 1980), modelos de ecuaciones estructurales (Bentler & Weeks, 1980), modelos de variable latente (Bishop, 1998), regresión logística ordinal (Harrell, 2001), regresión multinomial (Agresti, 2002) y en particular los modelos de regresión logística multinomial (So & Warren, 1995) y los modelos de elección (McFadden et al. , 1973).
El investigador Piccolo (2003 b) junto con algunos colaboradores desarrolló un nuevo enfoque para la modelación de respuestas discretas, conocido como modelos CUB (Combination of discrete Uniform and shifted Binomial random variables) cuya principal característica es el conocimiento de que las selecciones y preferencias están influenciadas por mecanismos psicológicos. Estos modelos consisten en una mezcla de dos distribuciones, que analizan y comparan la incertidumbre de las respuestas y el sentimiento de agrado/interés de los sujetos hacia los ítems de determinadas encuestas de evaluación o de preferencia (Iannario & Piccolo, 2009).
Algunos de los campos en los que se ha implementado el uso de los modelos CUB son: evaluaciones de enseñanza (D’Elia & Piccolo, 2005), sociología (Iannario, 2008), lingüística (Balirano & Corduas, 2008) , medicina (D’Elia, 2008), rendimiento de los servicios universitarios (Corduas et al., 2009), análisis de riesgos (Cerchiello et al., 2010), marketing (Iannario & Piccolo, 2010), análisis cuantitativo (Deldossi & Zappa, 2011), industria alimenticia (Iannario et al., 2012), relaciones laborales (Capecchi, 2015), envasado de alimentos (Arboretti & Bordignon, 2016), psicología (Zurlo et al., 2017), entre otros.
Con el objetivo de evaluar la calidad del ajuste obtenido al estimar un modelo CUB, en este artículo se propone usar los residuales. Sin embargo, ya que la variable respuesta es de tipo discreto y toma un número pequeño de valores, es necesario usar una definición alternativa: los residuales RQR (Randomized Quantile Residuals) propuestos por Dunn & Smyth (1996).
El resto del artículo se desarrolla de la siguiente manera: en la sección 2 se introducen los modelos CUB, en la sección 3 se describen los residuales RQR, su implementación en el paquete cubm y ejemplos referentes a la obtención y análisis de normalidad de los residuales, seguido de un estudio de simulación en la sección 4, algunas aplicaciones con datos reales en la sección 5 y por último en la sección 6 se presentan las conclusiones.
2. LOS MODELOS CUB
Los modelos CUB fueron propuestos por Piccolo (2006) como una herramienta alternativa para el análisis de datos derivados de las preferencias o contextos de evaluación. Su origen se basa en el hecho de que la preferencia expresada por el encuestado al calificar un producto o servicio en una escala de 1 a m, es el resultado de la mezcla de dos variables aleatorias: el sentimiento de agrado hacia el tema tratado y la incertidumbre alrededor de la selección (Gambacorta & Iannario, 2013).
Sea r la calificación expresada como la realización de una variable aleatoria R = {1,2,...,m}, se asume que R ∼ CUB(π,ξ,m) donde su función masa de probabilidad está dada por:
P(R = r) = (1−π)U(r)+πb(r,ξ) con r = 1,2,...,m, π ∈ (0,1] y ξ ∈ [0,1], (1)
donde la componente U(r), con peso asociado 1−π, es la incertidumbre o indecisión presente en cualquier elección humana; esta resulta de diferentes hechos relacionados con el proceso de evaluación como el conocimiento limitado del tema, la escala de respuesta, el interés personal hacia los ítems, ambigüedad de las preguntas, el tiempo dedicado a elaborar la elección, entre otros (Iannario et al., 2012).
Esta componente de incertidumbre puede ser modelada por medio de una distribución uniforme discreta de la forma: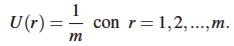
La componente b(r,ξ), con peso asociado π, es el nivel de agrado/interés hacia un producto dado y resulta de motivaciones subjetivas, tiene parámetro ξ y es modelada a través de una distribución binomial desplazada: 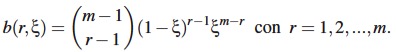
La distribución binomial desplazada (Oh, 2014), es muy útil, ya que es capaz de hacer frente a diferentes formas de los datos de una muestra con un único parámetro, además permite calificar un producto o servicio de 1 a m como usualmente se hace en la vida cotidiana.
En la estimación de los parámetros de modelos se consideran dos casos, el primero cuando sólo se tiene en cuenta la respuesta del encuestado y el segundo cuando además de la respuesta se tiene en cuenta información adicional del encuestado.
Para el primer caso, suponga que a un grupo de n personas se les solicita calificar un servicio o producto en una escala de 1 a m. Sea R la variable aleatoria y r1,r2,...,rn las calificaciones dadas por los integrantes del grupo. Si se asume que R ∼ CUB(π,ξ,m), entonces la función de log-verosimilitud ℓ(θ) con vector de parámetros del modelo θ = (π,ξ)⊤ está dada por:
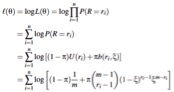
Para encontrar los estimadores de máxima verosimilitud del vector θ se pueden utilizar métodos numéricos. Algunos de los métodos numéricos utilizados dentro del cubm son: optim (un metodo basado en algoritmos de gradiente conjugado y de Nelder-Mead, cuasi-Newton), nlminb (un metodo sin restricciones y restringida en caja) y DEoptim (el algoritmo de evolución diferencial para la optimización global de una función de valor real de un vector de parámetros de valor real, (Mullen et al., 2011)).
Para el segundo caso, así como en los modelos de regresión usuales, en los modelos CUB es posible utilizar variables explicativas o covariables para modelar los parámetros π y ξ.
Suponga nuevamente que a un grupo de n personas se les solicita calificar un servicio o producto en una escala de 1 a m. Suponga además, que para cada persona se tiene información adicional como por ejemplo edad, estado civil, años de experiencia, salario, entre otras. Esta información adicional corresponde a las t covariables que se denotan por X1,X2,X3,...,Xt. En la siguiente tabla se muestra un resumen de la información disponible en un modelo CUB con covariables.
| Persona | Calificación R | X1 | X2 | X3 | ··· | Xt |
| 1 | r1 | x11 | x21 | x31 | ··· | xt1 |
| 2 | r2 | x12 | x22 | x32 | ··· | xt2 |
| ... | ... | ... | ... | ... | ... | ... |
| n | rn | x1n | x2n | x3n | ··· | xtn |
Asumiendo que las respuestas de las n personas se distribuyen CUB(πi,ξi,m), es posible modelar los parámetros de π y ξ usando subconjuntos de las t covariables mostradas en la Tabla 1.
Por ejemplo, el parámetro π para el i-ésimo individuo se puede modelar usando p de las t covariables así:
g(πi) = β0+β1x1i +β2x2i +···+βpxpi,
la expresión anterior se puede escribir en forma vectorial de la siguiente manera:
g(πi) = β⊤Zi, (3)
donde β=(β0,β1,...,βp)⊤ mientras que Zi =(1,x1i,x2i,...,xpi)⊤. La función g(·) en la expresión 3 se llama función de enlace y garantiza que los valores de β⊤Zi se mapeen correctamente en el intervalo (0,1] para generar valores correctos de π (Piccolo, 2006).
Dos opciones se tiene como función de enlace g(·), la primera es la función probit que se denota como Φ(·) y que representa la función de distribución acumulada de una normal estándar y la segunda opción es la función logit(·).
De forma similar, el parámetro ξ para el i-ésimo individuo se puede modelar usando q de las t covariables así:
g(ξ) = γ0+γ1x1i +γ2x2i +...+γqxqi,
la expresión anterior se puede también escribir en forma vectorial así: g(ξ) = γ⊤Wi, (4) donde γ = (γ0,γ1,...,γq)⊤ mientras que Wi = (1,x1i,x2i,...,xqi)⊤.
Sustituyendo las expresiones 3 y 4 en la expresión 1, se tiene que la función de masa de probabilidad queda expresada así:
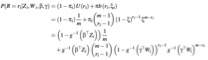
La función de
log-verosimilitud en este caso se escribe de la siguiente manera: 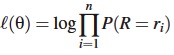
con P(R = ri) definido en la expresión 5. En este nuevo caso el vector de parámetros del modelo está dado por θ = (β,γ)⊤, cuyo estimador de máxima verosimilitud se obtiene por métodos numéricos.
3. RESIDUALES RQR (RANDOMISED QUANTIL RESIDUAL)
Sean y1,y2,...,yn observaciones independientes con función de densidad f(y,θ) y función de distribución acumulada F(y,θ) donde θ es el vector de parámetros y θˆ sus estimaciones.
Dunn & Smyth (1996) definen los cuantiles residuales aleatorizados rq,i como rq,i= Φ−1(ui), (7) donde Φ−1(·) es la inversa de la función de distribución acumulada de una variable normal estándar y los ui son cuantiles residuales, definidos de forma diferente para variables respuesta discretas y continuas ( Dunn & Smyth, 1996).
3.1. Residuales RQR cuando la variable respuesta tiene distribución discreta
Si y es una observación de una variable respuesta discreta, entonces F(y|θ) es una función paso con salto en los enteros y ∈ RY. La distribución de u = F(y|θ) tiene rango de cero a uno, pero es discreta con probabilidad positiva en los puntos F(y|θ), y ∈ RY. Para afrontar el hecho de que la distribución sea discreta, u es definido como un valor aleatorio de la distribución uniforme en el intervalo (Stasinopoulos et al., 2017).
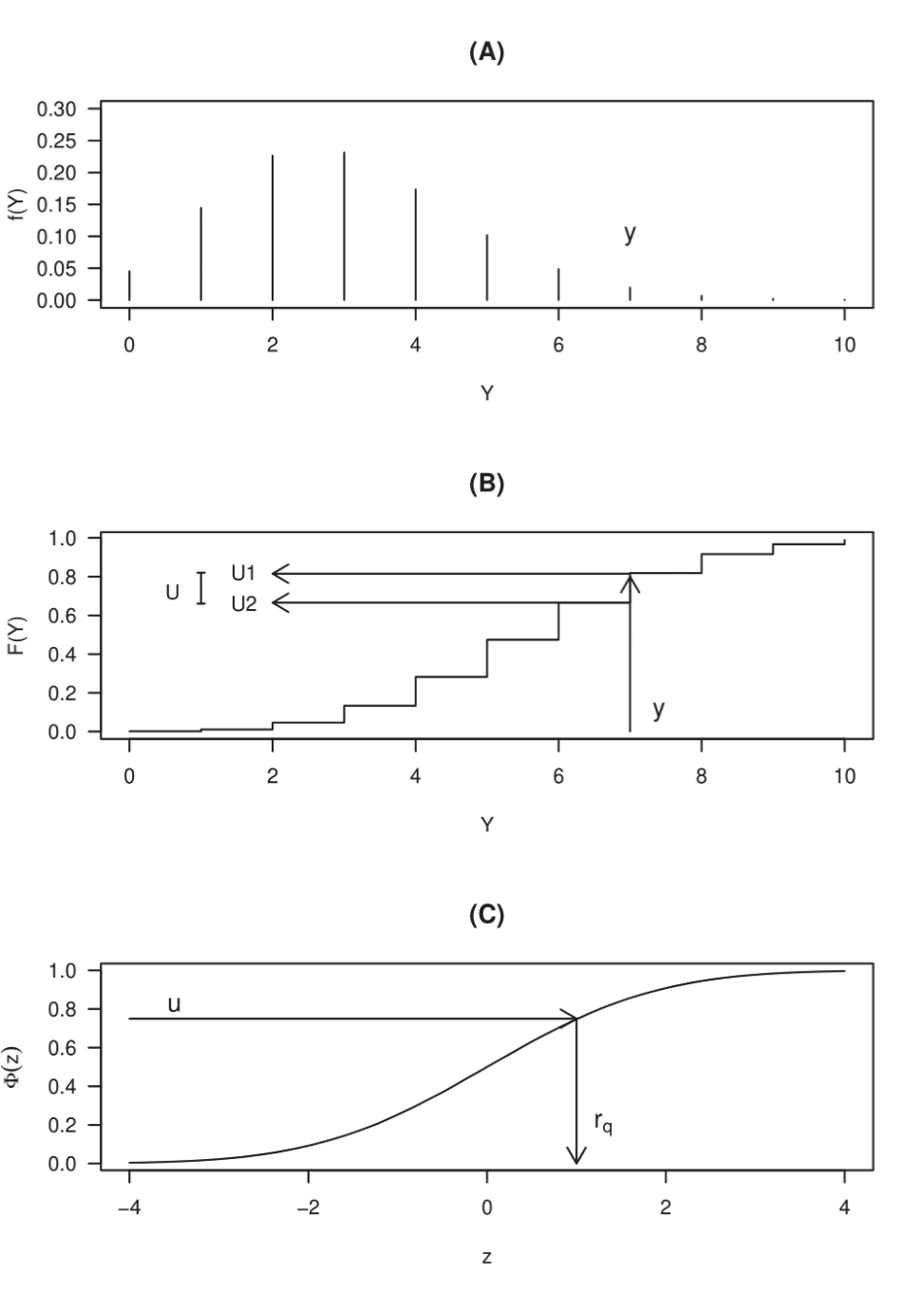
En la Figura 1, se ilustra la forma para obtener los residuales RQR cuando la respuesta es discreta
Elaboración propia.Al ajustar un modelo a un conjunto de datos, se busca evaluar si este modelo es adecuado, una de las formas que existen para verificar este hecho es la planteada en el libro de Stasinopoulos et al. (2017), quien afirma que el ajuste de un modelo es correcto si los cuantiles residuales aleatorizados RQR siguen una distribución normal estándar.
3.2. Función rqr
Con el fin de obtener los cuantiles residuales aleatorizados de forma automática, hemos creado la función rqr, la cual actualmente se encuentra implementada en el paquete cubm y tiene los siguientes argumentos:
y: un vector con la variable respuesta.
pi: valor o vector de valores para el parámetro π.
xi: valor o vector de valores para el parámetro ξ.
m: el valor máximo.
Para acceder a la última versión del paquete cubm que se encuentra alojada en un repositorio GitHub se puede consultar la dirección https://github.com/fhernanb/cubm. Cualquier usuario puede descargar el paquete cubm escribiendo el siguiente código en la consola de R.
[ commandchars=\\\{\ }] if (
! require(\textquotesingle\negthinspace\negthinspace\negthinspace devtools\textquotesingle)
)
install.packages( \textquotesingle\negthinspace\negthinspace\negthinspace devtools\textquotesingle )
devtools::install_github( \textquotesingle\negthinspace\negthinspace\negthinspace fhernanb/cubm\textquotesingle, force=TRUE )
A continuación se presentan ejemplos del uso de la función rqr para obtener los residuales RQR cuando los datos son ajustados a través de los modelos CUB y su uso para evaluar la calidad de un modelo ajustado.
Ejemplo usando datos simulados sin covariables
En este ejemplo se utiliza un conjunto de datos simulados para mostrar que los residuales RQR permiten determinar si el modelo está bien ajustado. El resumen de la estructura de los datos simulados es: 
Se simulan n=1000 observaciones del modelo anterior y usando la función cub se ajusta un modelo llamado mod1. La información de los parámetros se resume en la Tabla 2:
| Efectos fijos para probit(π) | ||
| Estimación Error estándar Valor z | Pr(> |z|) | |
| (Intercepto) | -1.04041 0.16423 -6.335 | 2.374×10−10 |
| Efectos fijos para probit(ξ) | ||
| Estimación Error estándar Valor z | Pr(> |z|) | |
| (Intercepto) | 0.12992 0.10308 1.2604 | 0.2075 |
Con las
estimaciones de la Tabla 2 se obtienen πˆ y ξˆ, así el modelo CUB ajustado es: 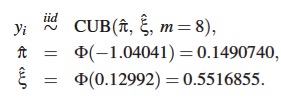
Del resultado anterior se ve que los estimadores de máxima verosimilitud del modelo son πˆ = 0.1490740 y ξˆ = 0.5516855, los cuales están muy cerca de los valores verdaderos π = 0.15 y ξ = 0.60.
Para veificar que el modelo ajustado es adecuado, se estiman dos residuales: (r1) del modelo mod1 y ( r 2) de un modelo erróneo obtenido con estimadores elegidos de forma arbitraria, π⋆ = 0.8 y ξ⋆ = 0.2 y se comprueba si estos tienen distribución N(0,1); para esto se construye un gráfico cuantil-cuantil.
En la Figura 2, se muestran los gráfico cuantil-cuantil para los residuales RQR del modelo estimado y del modelo erróneo. Los residuales para el modelo estimado por máxima verosimilitud están cerca de la línea de referencia y dentro de las bandas de confianza. Por el contrario, para el modelo erróneo que usó estimaciones elegidas caprichosamente, se ve que los residuales no siguen una distribución N(0,1).
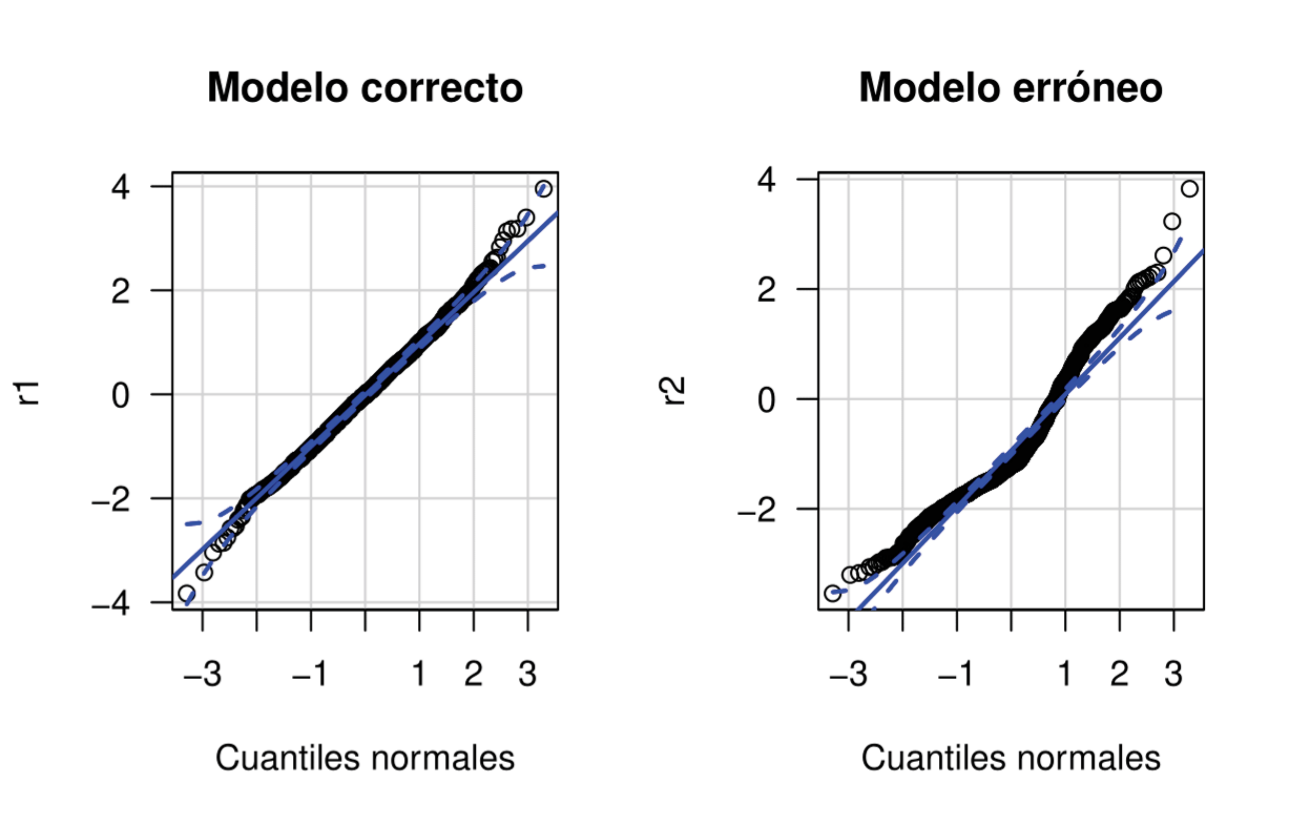
Adicional a los gráficos cuantil-cuantil, se aplicó la prueba de normalidad Kolmogorov-Smirnov a los residuales r1 y r2 y los resultados obtenidos son:
## One-sample Kolmogorov-Smirnov test
##
## data: r1
## D = 0.01868, p-value = 0.8763
## alternative hypothesis: two-sided
## One-sample Kolmogorov-Smirnov test
##
## data: r2
## D = 0.42599, p-value < 2.2e-16
## alternative hypothesis: two-sided
De los resultados de las pruebas se observa que el valor-p para r1 fue de 0.8763, indicando que no hay evidencias para rechazar que los residuales r1 siguen una distribución normal estándar. Por otro lado, el valor-p para la prueba de normalidad de r2 fue muy bajo indicando que los residuales r2 no siguen una distribución N(0,1).
Los patrones observados en la Figura 2 y los resultados de la pruebas de normalidad, se obtienen sin importar el conjunto de datos simulados bajo la función rcub. Eso significa que los residuales RQR son una buena herramienta para determinar si el modelo está bien ajustado.
Además de los residuales, existen otras medidas que permiten determinar la calidad del ajuste obtenido como lo son el índice de disimilitud (Diss) el coeficiente F2y el índice I, las cuales fueron implementadas en R y tratadas con detalle en Mazo (2018). El primer índice, propuesto por Simonoff (2003), mide la proporción de personas encuestadas que deben cambiar su selección para lograr un ajuste perfecto y se define: Diss = 12 r∑=m 1 |fr − pr(θ ˆ)|, (9) donde fr representa la frecuencia relativa observada para la r-ésima respuesta, pr(θˆ) representa la frecuencia relativa estimada para la r-ésima respuesta bajo el modelo CUB, m es el número de posibles respuestas y θˆ es el vector de parámetros estimados que contiene a πˆ y ξˆ.
El índice Diss toma valores entre 0 y 1, valores cercanos a 0 significan que la distribución obtenida con el ajuste del modelo CUB es semejante a la distribución observada en los datos, mientras que valores de Diss cercanos a 1 indican problemas de ajuste. Según Simonoff (2003), valores por encima de 0.10 sugieren falta de ajuste.
El coeficiente F2 propuesto por Iannario (2009) es una medida de ajuste normalizado para los modelos CUB, la cual compara la frecuencia relativa observada (fr) con la probabilidad estimada por el modelo (pr(θˆ)) , con el objetivo de cuantificar la magnitud de la desigualdad existente entre ellas. En ocasiones es usado para analizar la adecuación del modelo. Ésta medida puede ser calculada a través de: F2 = 1−Diss
El coeficiente F2 toma valores entre 0 y 1 que pueden ser interpretados como la proporción de respuestas pronosticadas correctamente (Iannario et al., 2012).
El tercero, el índice I, también planteado por Iannario (2009) es una medida que compara las entropías de las frecuencias relativas (observadas) y las probabilidades CUB (estimadas), con respecto a la distribución uniforme. La expresión para obtenerlo es: 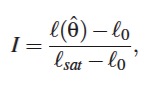
donde ℓ(θˆ), ℓ0 y ℓsat son la log-verosimilitud del modelo CUB estimado, la log-verosimilitud de un modelo uniforme y la log-verosimilitud de un modelo saturado, respectivamente.
El índice I toma valores entre 0 y 1, los valores son cercanos a 0 se dan cuando la probabilidad estimada pr(θˆ) es próxima a una distribución uniforme y asume valores cercanos a 1 si se consigue un ajuste perfecto. 
Para el caso del mod1, el valor obtenido para el índice Diss indica que las diferencias entre la frecuencia relativa observada (fr) y la frecuencia relativa estimada pr(θˆ) son probablemente de poca importancia práctica, conclusión que es apoyada por los resultados obtenidos para el F2 que indica que la proporción de respuestas pronosticadas corrctamente es muy alta y para el índice I, que sugiere que el modelo CUB sin covariables es un buen candidato para ajustar los datos simulados, lo que además permite confirmar la inferencia obtenida a través de los residuales.
Ejemplo usando datos simulados con covariables
Se utiliza un conjunto de datos simulados con covariables para mostrar que incluso, al incluir covariables en el ajuste, los residuales RQR permiten determinar si el modelo está bien ajustado.
La estructura de los datos simulados se resume a continuación 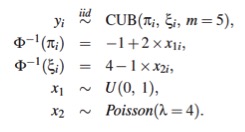
El vector de parámetros para el modelo anterior es Θ = (β0 = −1,β1 = 2,γ0 = 4,γ1 = −1)⊤. Se simulan n = 500 observaciones del modelo anterior y se ajusta un modelo llamado mod3.
| Estimación Error estándar Valor z | Pr(> |z|) | |
| (Intercept) | -0.83172 0.22910 -3.6304 | 0.000283 |
| x1 | 1.84786 0.37898 4.8760 | 1.083×10−06 |
| Efectos fijos para probit(ξ) | ||
| Estimación Error estándar Valor z | Pr(> |z|) | |
| (Intercept) | 3.704020 0.375106 9.8746 | < 2.2×10−16 |
| x2 | -0.935473 0.094134 -9.9377 | < 2.2×10−16 |
Del resultado en la Tabla 3 se observa que los estimadores de máxima verosimilitud para el modelo son Θˆ = (−0.83,1.85,3.70,−0.94)⊤, los cuales están muy cerca del verdadero vector de parámetros Θ = (−1,2,4,−1)⊤.
Emulando el proceso del ejemplo 3.2, se considera un modelo erróneo (mod4), donde la variable x2 explica a π y la variable x1 explica a ξ y se construyen los residuales RQR para ambos modelos (r3 y r4), usando los valores πˆi y ξˆi en cada caso.
Para verificar si los residuales r3 y r4 tienen distribución N(0,1), se construye un gráfico cuantil-cuantil para ambos.
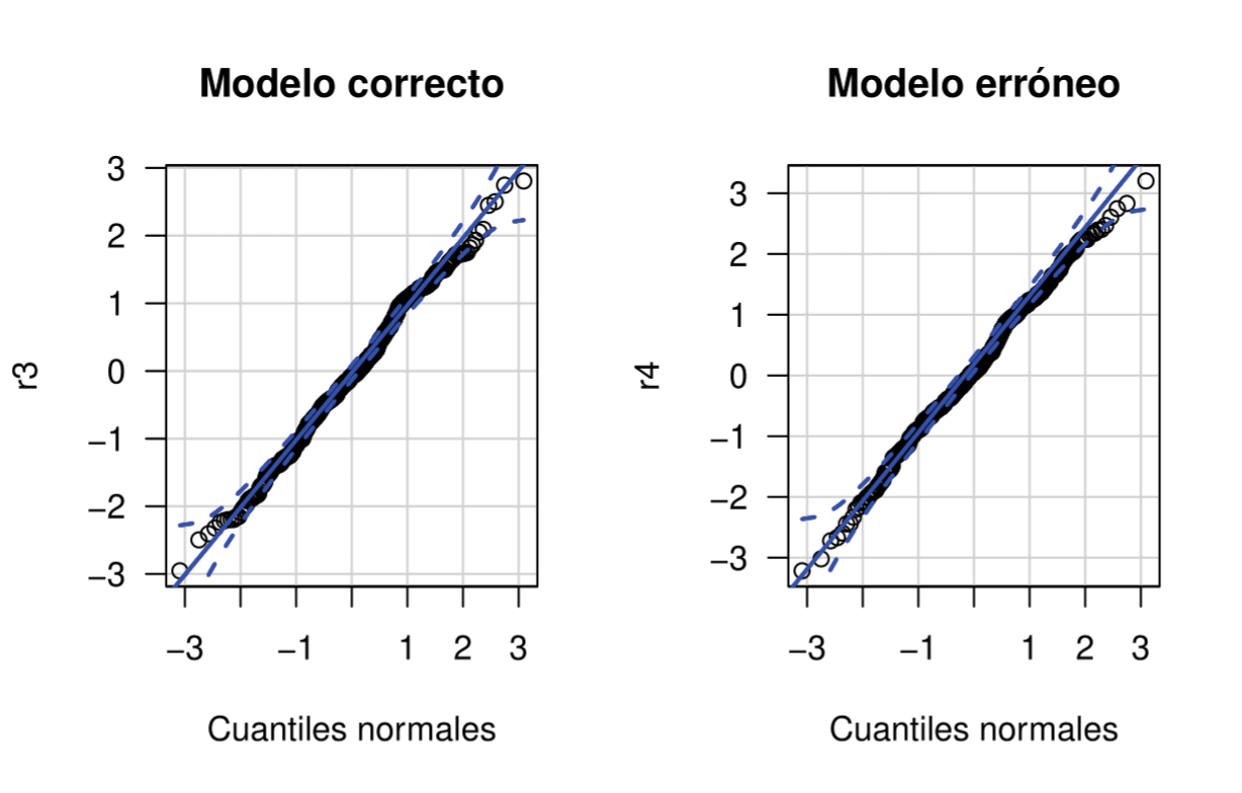
En la Figura 3, se muestran los gráficos cuantil-cuantil para los residuales RQR del modelo estimado y del modelo arbitrario, en la que se observa que los residuales para el modelo estimado por máxima verosimilitud, están cerca de la línea de referencia y dentro de las bandas de confianza. Por el contrario, para el modelo arbitrario, que usó estimaciones elegidas caprichosamente, se ve que los residuales no siguen una distribución N(0,1).
Adicional a los gráficos cuantil-cuantil, se aplicó la prueba Kolmogorov-Smirnov a los residuales r3 y r4 para saber si provenían de una población N(0,1) y se obtuvo:
## One-sample Kolmogorov-Smirnov test
##
## data: r3
## D = 0.036869, p-value = 0.505
## alternative hypothesis: two-sided
## One-sample Kolmogorov-Smirnov test
##
## data: r4
## D = 0.092421, p-value = 0.0003903
## alternative hypothesis: two-sided
De los resultados, se observa que el valor-p para la prueba de normalidad de r3 fue de 0.505, lo que indica que no hay evidencias para rechazar que los residuales r3 siguen una distribución normal estándar. Por otro lado, el valor-p para la prueba de normalidad de r4 fue muy bajo, indicando que los residuales r4 no siguen una distribución N(0,1).
Los patrones observados en la Figura 3 y los resultados de la pruebas de normalidad, se obtienen sin importar el conjunto de datos simulados con la función rcub. Eso significa que los residuales RQR son una buena herramienta para determinar si el modelo está bien ajustado  .
.
Como el resultado del índice Diss para el mod3 es más pequeño que el del mod4, entonces se puede decir que es mejor el mod3, además como el valor del coeficiente F2 es muy cercano a 1, es posible concluir que la proporción de respuestas predichas de forma correcta es muy alta y por tanto que el modelo ajustado es adecuado.
4. ESTUDIO DE SIMULACIÓN
En esta sección se presentan los resultados de un estudio de simulación para explorar el comportamiento de los residuales asociados a un modelo donde se consideran covariables para la estimación de los parámetros. La estructura considerada es el modelo descrito en el segundo ejemplo de la anterior sección. 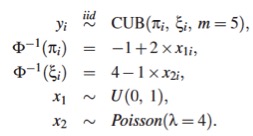
Para la simulación se consideraron tamaños muestrales n = 100,125,150,··· ,500, con cada n considerado, se simularon 100 observaciones que se usaron para estimar el modelo y los respectivos residuales, a los que se les aplicó el test de normalidad Shapiro-Wilk.
Los resultados obtenidos se presentan en la Figura 4, donde se puede observar que el porcentaje de rechazo de la hipótesis nula (datos con disribución normal) en la prueba de normalidad es muy bajo y que incluso con tamaños de muestras pequeños, la proporción de casos de residuales no normales no supera el 10 %.
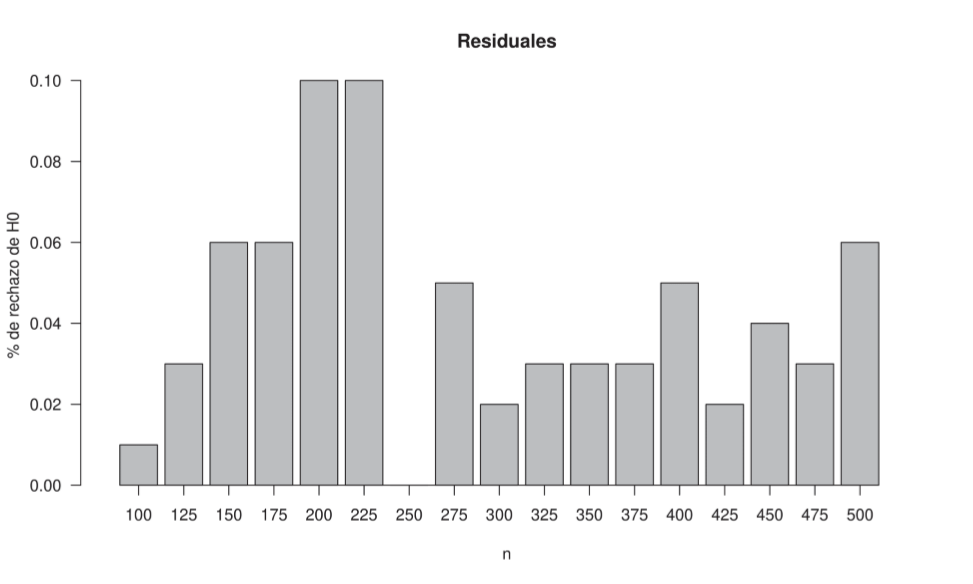
5. APLICACIONES
5.1. Datos reales sin covariables
Con la finalidad
de mostrar la utilidad de los modelos CUB con datos obtenidos en la vida
cotidiana, sin tener en cuenta ningún otro tipo de información, excepto, la
respuesta a una pregunta, se usa a continuación la base de datos condom, que contiene información
recolectada como parte de un estudio realizado en Medellín en el año 2013
acerca del uso del condón. En el estudio la variable respuesta, usecondom, corresponde a la opinión de los 153
participantes respecto a la frecuencia de uso del condón en una escala de 1 a
4, donde 1 = siempre, 2 = frecuentemente, 3 = ocasionalmente y 4 = nunca. En
este caso se usa un modelo CUB sin covariables como
se ve a continuación: 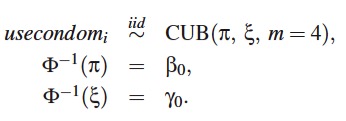
El modelo es llamado mod5 y en la siguiente tabla se muestra un resumen para la estimación de los parámetros π y ξ.
| Estimación Error estándar Valor z | Pr(> |z|) | |
| (Intercepto) | -0.19813 0.29902 -0.6626 | 0.5076 |
| Efectos fijos para probit(ξ) | ||
| Estimación Error estándar Valor z | Pr(> |z|) | |
| (Intercepto) | 0.69203 0.18243 3.7934 | 0.0001486 |
De acuerdo a lo anterior, el parámetro de incertidumbre, 1−πˆ, es 0.5785283 y el parámetro de agrado, 1−ξˆ, es 0.2444592, esto permite concluir que a la hora de responder este tipo de encuestas, las personas lo hacen con mayor grado de incertidumbre en la elección, que simpatía o agrado hacia el tema.
Teniendo en cuenta que si los residuales RQR se distribuyen normal, el modelo está bien ajustado, se construyen los residuales RQR de mod5, denotados r5, y se genera un gráfico cuantil-cuantil para verificarlo.
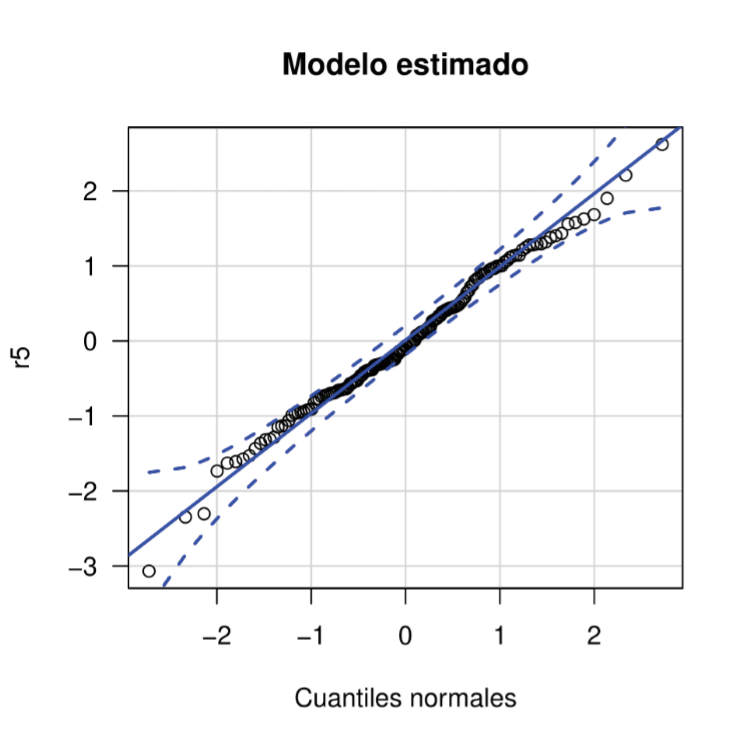
En la figura 5, se observa que los residuales para el modelo estimado por máxima verosimilitud están cerca de la línea de referencia y dentro de las bandas de confianza, concluyendo que la distribución de los residuales RQR es normal.
Como parte de la verificacción de normalidad de los residuales, se aplica la prueba Kolmogorov-Smirnov a los residuales r5, cuyo resultado muestra un valor-p de 0.9116 que lleva a concluir que los datos provienen de una distribución normal y de este modo, el modelo CUB ajustado sin tener más información de los encuestados que la respuesta, es adecuado.
## One-sample Kolmogorov-Smirnov test
##
## data: r5
## D = 0.045334, p-value = 0.9116
## alternative hypothesis: two-sided
Con el ánimo de corroborar la conclusión obtenida con los residuales, se obtuvieron los valores para algunos ídices de los cuales se infiere que el modelo estimado es adecuado (de acuerdo a I), hay poca diferencia entre la frecuencia relativa observada y la frecuencia relativa estimada (de acuerdo al Diss) y además, la proporción de respuestas predichas correctamente es muy alta (de acuerdo a F2).
Diss F2 I
## 0.00127877 ## 0.9987212 ## 0.9999174
5.2. Datos reales con covariables
En este ejemplo se analiza la base de datos univer (tomada de Iannario et all, 2016), en ella se encuentra registrada la información de la encuesta realizada a 13 facultades de la Universidad de Nápoles en Italia, en la cual se solicitó a los participantes que expresaran su opinión sobre los servicios de orientación en una escala de 7 puntos que va desde 1 = muy insatisfecho hasta 7 = extremadamente satisfecho. La base de datos tiene doce covariables (faculty, freqserv, age, lage, gender, diploma, residence, changeFa, informat, willingn, officeho, compete, and global) y 2179 observaciones; la variable llamada global, es la opinión de los participantes y corresponde a la variable respuesta.
Con el objetivo de mostrar que al incluir covariables en el ajuste del modelo, los residuales RQR permiten determinar si el modelo está bien ajustado, se propone un modelo para describir la satisfacción global, teniendo en cuenta la variable lage para estimar el parámetro π y la variable freqserv para estimar a ξ. El modelo considerado es: 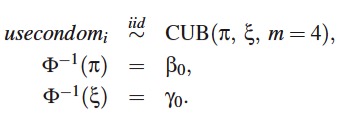
Luego se ajusta el modelo llamado mod6, se obtiene la información del modelo estimado cuyos resultados pueden verse en la tabla 5. Seguidamente,se construyen los residuales RQR asociados a mod6, se genera un gráfico cuantil-cuantil y se aplica una prueba de normalidad de los cuales se obtienen como resultados:
| Estimación Error estándar Valor z | Pr(> |z|) | |
| (Intercept) | 1.168513 0.060707 19.2485 | < 2×10−16 |
| lage | 0.572507 0.422961 1.3536 | 0.1759 |
| Efectos fijos para probit(ξ) | ||
| Estimación Error estándar Valor z | Pr(> |z|) | |
| (Intercept) | -0.828534 0.019157 -43.251 | < 2×10−16 |
| freqserv1 | -0.338487 0.033547 -10.090 | < 2×10−16 |
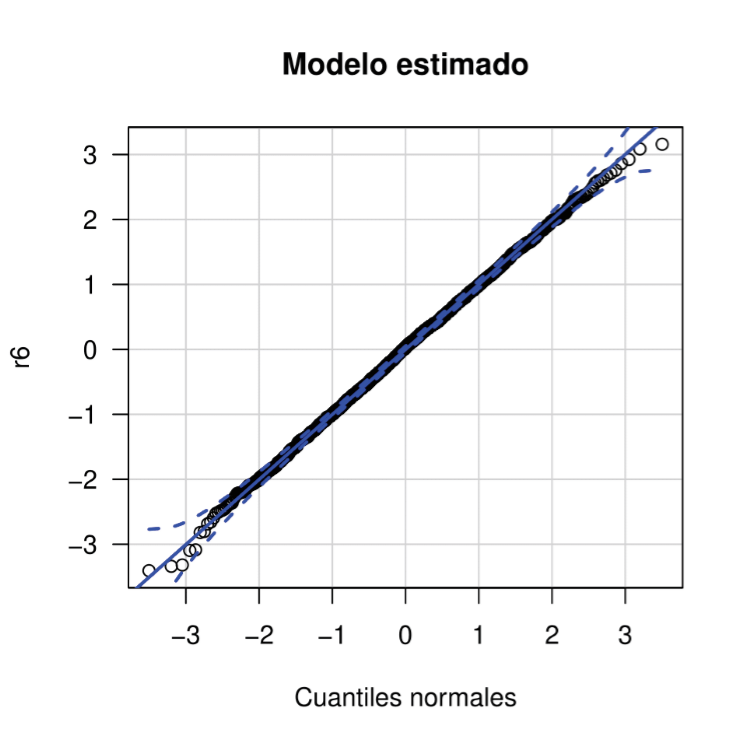
En la Figura 6, se observa que los residuales para el modelo estimado por máxima verosimilitud están cerca de la línea de referencia y dentro de las bandas de confianza, de este modo se puede inferir que la distribución de los residuales RQR es normal.
## One-sample Kolmogorov-Smirnov test
##
## data: r6
## D = 0.016087, p-value = 0.6256
## alternative hypothesis: two-sided
Adicionalmente, de acuerdo a los resultados de la prueba Kolmogorov-Smirnov aplicada a los residuales r6 con valor-p mayor a 0.5, es posible confirmar que estos provienen de una población N(0,1) y por tanto que el modelo CUB obtenido usando covariables para la extimación de π y ξ es adecuado.
Diss F2
## 0.02005078 ## 0.9799492
Los resultados obtenidos para los ídices Diss y F2 ratifican la conclusión obtenida con los residuales, ya que muestran que la proporción de respuestas predichas incorrectamente es muy pequeña y por tanto el modelo ajustado es apropiado.
6. CONCLUSIONES
En este artículo se propusieron los residuales RQR (Randomized Quantile Residuals) como herramienta para determinar la pertinencia del ajuste de un modelo CUB en presencia y ausencia de covariables, además se pudo evidenciar la aplicabilidad de la función implementada en el paquete cubm en ejemplos con datos reales y simulados en los que se obtuvieron los resultados esperados tanto de modelos bien ajustados como de modelos poco adecuados
Del estudio de simulación es posible concluir que sin importar el tamaño de la muestra la proporción de modelos incorrectamente diagnosticados es muy baja, sin embargo es necesario seguir realizando estudios de simulación que permitan describir otras características de los modelos ajustados a través de los residuales.
Referencias
Agresti, Alan. (2002). Categorical Data Analysis. Second Edition. John Wiley & Sons. New York, U.S.A. 721 p.
Arboretti, Rosa & Bordignon, Paolo. (2016). Consumer preferences in food packaging:Cub models and conjoint analysis. British Food Journal 118(3), 527-540.
Balirano, Giuseppe & Corduas, Marcella. (2008). Detecting semiotically-expressed humor in diasporic TV productions. Humor-International Journal of Humor Research. 21(3), 227-251.
Bentler, Peter & Weeks, David. (1980). Linear structural equations with latent variables. Psychometrika 45(3), 289-308.
Bishop, Christopher. (1998). Learning in graphical models: Latent variable models. Springer. 371-403.
Capecchi, S. (2015). Modelling the perception of conflict in working conditions. Electronic Journal of Applied Statistical Analysis 8(3), 298-311.
Cerchiello, P., Iannario, M., Piccolo, D. (2010). Assessing risk perception by means of ordinal models. Mathematical and Statistical Methods for Actuarial Sciences and Finance. 75-83.
Corduas, M., Iannario, M. & Piccolo, D. (2009). A class of statistical models for evaluating services and performances.Statistical methods for the evaluation of educational services and quality of products. 99-117.
Deldossi, L. & Zappa, D. (2011). Measurement errors and uncertainty: a statistical perspective. In: New Perspectives in Statistical Modeling and Data Analysis. Berlin, Heidelberg. 145-153.
D’Elia, A. (2008). A statistical modelling approach for the analysis of TMD chronic pain data. Statistical Methods in Medical Research. 17 (4), 389-403.
D’Elia, A. & Piccolo, D. (2005). A mixture model for preferences data analysis. Computational Statistics & Data Analysis. 49(3), 917-934.
Dunn, P. & Smyth, G. (1996). Randomized quantile residuals. Journal of Computational and Graphical Statistics. 5(3), 236-244.
Gambacorta, R. & Iannario, M. (2013). Measuring job satisfaction with CUB models. Labour. 27(2), 198224.
Harrell, F. (2001). Regression modeling strategies: Ordinal logistic regression. Springer, New York. 331343.
Iannario, M. (2008). A class of models for ordinal variables with covariates effects. Quaderni di Statistica. 10, 53-72.
Iannario, M. (2009). Fitting measures for ordinal data models, Quaderni di Statistica. 11, 39-72
Iannario, M. and Piccolo, D. (2009). A program in R for CUB models inference. Version 2.
Iannario, M. & Piccolo, D. (2010). A New Statistical Model for the Analysis of Customer Satisfaction. Quality Technology & Quantitative Management. 7(2), 149-168.
Iannario, M., Manisera, M., Piccolo, D. & Zuccolotto, P. (2012). Sensory analysis in the food industry as a tool for marketing decisions. Advances in Data Analysis and classification. 6 (4), 303-321.
Mazo, D. (2018). Implementación de pruebas diagnósticas en R para modelos CUB (Tesis de Maestría). Universidad Nacional de Colombia, Medellín.
Mullen, K., Ardia, D., Gil, D., Windover, D. & Cline, J.(2011). DEoptim: An R package for global optimization by differential evoluti.on. Journal of Statistical Software. 40(6 ), 1-26.
McCullagh, P. (1980). Regression models for ordinal data. Journal of the royal statistical society. Series B (Methodological). 42(2), 109-142.
McFadden, D. et al.(1973). Conditional logit analysis of qualitative choice behavior. Institute of Urban and Regional Development, University of California Berkeley, CA
Oh, Ch. (2014). A maximum likelihood estimation method for a mixture of shifted binomial distributions. Journal of the Korean Data and Information Science Society. 25(1), 255-261.
Piccolo, D. (2003) B. On the moments of a mixture of uniform and shifted binomialrandom variables. Quaderni di Statistica. 5(1), 85-104.
Piccolo, D. (2006). Observed information matrix for MUB models.Quaderni di Statistica. 8, 33-78.
R Core Team. (2019). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. *https://www.R-project.org/
Simonoff, J. (2003). Analyzing categorical data. Springer Science & Business Media. New York.
So, Y. & Kuhfeld, F. (1995). Multinomial logit models in SUGI 20 Conference Proceedings. 1227-1234.
Stasinopoulos, M., Rigby, R., Heller, G., Voudouris, V., De Bastiani, F.(2017). Flexible Regression and Smoothing: Using GAMLSS in R. New York, U.S.A. 571 p.
Zurlo, M., Iannario, M. & Piccolo, D. (2017). Dimensioni dello stress e salute psicologica degli insegnanti: validazione di un modello di rischio attraverso la metodologia CUB per l’analisi di dati ordinali. Psicologia della salute.

