



Artículos
Análisis de interpolación espacial de contagios de COVID-19 en la cuenca del río Luján
Analysis of spatial interpolation of COVID-19 infection in the Luján river basin
Geograficando
Universidad Nacional de La Plata, Argentina
ISSN: 2346-898X
Periodicidad: Semestral
vol. 17, núm. 2, e099, 2021
Recepción: 31 Mayo 2021
Aprobación: 16 Julio 2021
Publicación: 01 Noviembre 2021
Resumen: Uno de los factores que se debe tener en cuenta cuando se analiza la propagación de un virus es el geográfico o espacial, que condiciona su proceso de difusión espacial, a partir de las relaciones funcionales que se presentan en el espacio geográfico. El presente trabajo desarrolla la propuesta metodológica basada en el método de interpolación espacial denominado Estimador de Densidad Kernel, orientado a la modelización cartográfica de densidades continuas, considerando la tasa de contagios de COVID-19. El área de estudio corresponde a los municipios de la cuenca del río Luján (Argentina). Los resultados cartográficos evidencian una marcada diferenciación espacial de la incidencia de los contagios en el interior de los municipios del área de estudio, y definen sectores de mayor dinamismo en la propagación espacio-temporal del virus.
Palabras clave: Interpolación espacial, Densidad Kernel, Sistemas de Información Geográfica, Cuenca del río Luján.
Abstract: One of the factors that must be taken into account when analyzing the spread of a virus is the geographic or spatial factor, which conditions its spatial diffusion process based on the functional relations occurring in geographic space. This article develops the methodological proposal based on the spatial interpolation method called Kernel Density Estimation, which aims at cartographic modeling of continuous densities, considering the COVID-19 infection rate. The study area corresponds to the municipalities of the Luján river basin (Argentina). The cartographic results show a marked spatial differentiation of the incidence of infection within the municipalities in the study area, defining sectors of greater dynamism in the spatio-temporal spread of the virus.
Keywords: Spatial interpolation, Kernel Density, Geographic Information Systems, Luján River Basin.
Introducción
En el contexto de pandemia generada por el COVID-19, la Geografía se ha presentado como una disciplina central dentro de las Ciencias Sociales, pues generó aportes sobre la distribución y evolución espacial del COVID-19 en distintas escalas espaciales. Podemos mencionar los primeros resultados cartográficos a nivel mundial, con datos en tiempo real, de la propagación del virus en los distintos países,1 cuestión que remarcó el desarrollo actual de la cartografía como herramienta geotecnológica,2 ligada no sólo al ámbito académico sino a toda la sociedad. La Geografía Cuantitativa, en su carácter de ciencia espacial aplicada (Buzai, 2020), se centra en la búsqueda de generalidades y regularidades en el análisis del espacio geográfico, y genera conocimientos a un nivel de focalización espacial, apoyado en conceptos como los de localización, distribución espacial, asociación espacial, interacción espacial y evolución espacial, que se hacen operativos bajo la metodología del análisis espacial cuantitativo basada en el uso de Sistemas de Información Geográfica (SIG). Uno de los factores que se debe tener en cuenta cuando se analiza la propagación de un virus es el geográfico o espacial, que condiciona el proceso de difusión espacial de cualquier enfermedad (Humacata, 2020), a partir de las relaciones funcionales que se presentan en el espacio geográfico. En este sentido, el presente trabajo va a desarrollar el concepto de interacción espacial y la aplicación metodológica basada en un método de interpolación espacial, denominado Estimador de Densidad Kernel. La propuesta metodológica se orienta a la modelización cartográfica de densidades continuas, considerando la tasa de contagios de COVID-19 en los municipios de la cuenca del río Luján (Provincia de Buenos Aires, Argentina). A partir de los resultados cartográficos, se avanza en el análisis de la distribución espacio-temporal de las densidades de contagios. Estos resultados se presentan como aportes que la Geografía puede realizar en el ámbito de la planificación y gestión territorial a nivel urbano-regional.
Análisis de interacción espacial
La interacción espacial es un tema central en la teoría locacional (Haggett, 1975). Hace referencia a la existencia de flujos horizontales entre distintas entidades distribuidos sobre el espacio geográfico, que dan lugar a un espacio relacional que presenta los vínculos que se establecen entre las localizaciones (Buzai, 2010; Pumain y Saint Julien, 2014), bajo la influencia de determinados factores de localización, como la distancia definida como fricción espacial. Este aspecto hace referencia a una propiedad de la Geografía que indica la interdependencia de las localizaciones; es decir, que todas las entidades geográficas están relacionadas y que aquellas más cercanas guardan una mayor relación (Tobler, 1970), manteniendo una proporcionalidad decreciente que depende de la ubicación de cada localización.
El análisis de interacción espacial se orienta a medir las relaciones funcionales entre entidades geográficas con la finalidad de descubrir la estructura funcional del espacio geográfico. Dentro de esta línea de investigación, se encuentran los estudios de áreas de influencia, de accesibilidad y de interacción espacial, enmarcados en los modelos gravitatorios de la física social, en lo que se ha denominado Macrogeografía (Warntz, 1975). Desde esta postura, la interacción espacial se basa en la relación entre el espacio absoluto y relativo, a partir de considerar cada localización y su factor de diferenciación espacial como peso que ejerce influencia sobre las otras localizaciones, y la distancia como factor de fricción espacial, como medida de la influencia de la interdependencia espacial.
Desde un abordaje principalmente espacial, la Geografía en su vertiente cuantitativa y racionalista ha desarrollado relevantes avances en la sistematización de procedimientos analíticos con la finalidad de determinar patrones de distribución espacial. En este sentido, la tecnología de los Sistemas de Información Geográfica (SIG) ha posibilitado la obtención de resultados cartográficos y numéricos de suma utilidad en el ámbito de la planificación y gestión territorial. Los avances en la modelización espacial mediante técnicas cuantitativas apuntan a una mayor capacidad para el análisis y visualización de datos espaciales (Unwin, 1996). El alcance temático de los modelos de interacción espacial ha presentado un fuerte crecimiento, acompañado por los adelantos en las geotecnologías, que permiten la automatización de técnicas de análisis espacial y una mayor integración con modelos matemáticos y estadísticos. En este sentido, con base en Buzai y Baxendale (2013) podemos señalar algunos procedimientos de interacción espacial en el ámbito de los SIG, tales como la generación de buffers y polígonos de Thiessen para la determinación de áreas de influencia; isolíneas de accesibilidad (ideal, real, calidad en la comunicación, trayectorias); potencial de población para cálculos de interacción espacial de servicios; y estimación de superficies continuas para el cálculo de probabilidades espaciales.
Desde la perspectiva del análisis de interpolación espacial, el espacio geográfico representado en una superficie discreta, con valores que se distribuyen de manera uniforme en cada unidad espacial, se modeliza para lograr una superficie continua, a partir de la creación de una matriz de información en formato de capa temática raster, cuyas celdas contienen información de la densidad de contagios. De esta manera, se pretende obtener la tendencia de la distribución de la densidad de puntos y su variación espacial. En este sentido, los procedimientos se orientan a la determinación de densidades continuas, que representan la probabilidad de que un punto tenga cierto valor de densidad de contagios, según su posición frente a puntos conocidos o de referencia. En el caso de estudio, se cuenta con datos a nivel de municipios (unidades político-administrativas), cuyo nivel de desagregación espacial no resulta adecuado cuando se pretende un análisis al interior de cada unidad espacial, con la finalidad de verificar el comportamiento espacio-temporal del COVID-19, como difusión de la enfermedad desde las ciudades cabeceras (como centro de mayor concentración de contagios) de cada municipio hacia las localidades menores. Estas se encuentran distribuidas en el espacio funcional y mantienen relaciones de contigüidad e interacción con unidades espaciales vecinas, y cuya influencia tiende a variar con la distancia. En este sentido, resulta pertinente aplicar la metodología de interpolación espacial, con la finalidad de llegar a la modelización cartográfica que nos indica la distribución de la densidad continua de casos confirmados, cuya configuración hace referencia a la estimación de la ocurrencia de contagios en un espacio continuo de variaciones internas.
Materiales y métodos
La base cartográfica
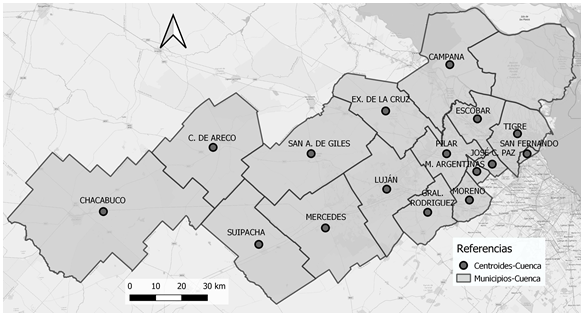
La base cartográfica digital, proveniente del Instituto Geográfico Nacional (IGN), contiene las entidades areales correspondientes a unidades político-administrativas. El área de estudio (Figura 1), ubicada en el sector noreste de la provincia de Buenos Aires (Argentina), está compuesta por dieciséis municipios: Campana, Carmen de Areco, Chacabuco, Escobar, Exaltación de la Cruz, General Rodríguez, José C. Paz, Luján, Malvinas Argentinas, Mercedes, Moreno, Pilar, San Andrés de Giles, San Fernando, Suipacha y Tigre. Cuenta con una superficie de 11.552 km2 y una población total de 2.570.889 personas, según el Censo Nacional de Población, Hogares y Viviendas del año 2010 (INDEC, 2013).
A partir de esta base cartográfica en SIG vectorial, se procedió a calcular los centroides de cada unidad espacial (Municipios), y a generar la capa temática de base para la posterior aplicación metodológica de interpolación espacial.
Variables
La base de datos alfanumérica contiene variables relativas al COVID-19, obtenidas del Ministerio de Salud de la República Argentina (2020), que pone a disposición un reporte diario de cantidad de personas contagiadas de COVID-19 a nivel departamental, a partir del cual se seleccionaron datos acumulados mensuales (10 registros en valores absolutos), desde el 30 de marzo al 28 de diciembre de 2020. Se procedió a la sistematización de los datos en una Matriz de Datos Originales (MDO) organizada en filas (unidades espaciales) y columnas (variables), como base de datos alfanumérica asociada a la base cartográfica en un ambiente geoinformático. El tratamiento matricial de la información avanza en una secuencia que permite obtener variables relativas que integran la Matriz de Datos Índice (MDI). En esta instancia se procedió al cálculo de la tasa de contagios por cada cien mil habitantes (TC= (Total de contagios/Población) * 100.000), y se obtuvieron 10 variables en valores relativos, correspondientes al periodo temporal bajo estudio.
Metodología de interpolación espacial mediante estimador Kernel
La distribución espacial de una variable en el espacio geográfico no se presenta de forma homogénea sino más bien de forma irregular. Presenta áreas con mayores concentraciones de valores, y llega a definirse una serie de pautas de distribución espacial que responden a determinados patrones espaciales. Desde el análisis espacial cuantitativo (Buzai, Baxendale, Humacata y Principi, 2016) se trabaja con bases de datos georreferenciadas, que contienen la cartografía digital y la información alfanumérica (variables), en formato de capas temáticas de tipo vectorial (puntos, líneas y áreas) o raster (celdas). La información puede provenir de fuentes directas o indirectas, dependiendo de la naturaleza y la magnitud de la investigación. En este sentido, resulta fundamental el nivel de desagregación espacial; es decir, a qué unidades espaciales está referida la información. Cuando se trabaja con fuentes oficiales comúnmente se consideran unidades político-administrativas, cuya forma y extensión no representan de forma correcta la distribución espacial de los fenómenos, lo que genera una imagen distorsionada de la realidad bajo estudio (Moreno Jiménez, 1991). En otros casos, la información se encuentra limitada sólo a algunas áreas, como las estaciones meteorológicas o muestras de altitud del terreno, lo que hace imposible contar con una distribución uniforme que abarque la totalidad del área de estudio. Frente a estos problemas de carácter metodológico, en los que se requieren procedimientos indirectos de cálculo, la Geografía Cuantitativa se sirve de métodos estadísticos que le permiten arribar a soluciones a partir de los métodos de interpolación espacial.
La interpolación espacial hace referencia a la estimación de valores desconocidos en distintas localizaciones a partir de un conjunto de puntos con valores conocidos (Buzai y Baxendale, 2011). Es decir que, a partir de un conjunto de observaciones, denominada muestra, en un espacio discreto, se calculan valores de probabilidad en un espacio continuo, al que se denomina superficie estadística, ya que el resultado es una función de probabilidad con valores proyectados. Existe una gran variedad de métodos de interpolación espacial, desde los más simples basados en técnicas de triangulación, como los polígonos de Thiessen, hasta los que se apoyan en una matriz en formato de grilla regular, como Kernel, Inverso de la Distancia (IDW) y kriging, entre otros3. El campo de aplicación también es amplio y en aumento, y es posible su implementación para la generación de modelos digitales del terreno (Bosque Sendra y García, 2001), modelización cartográfica de isócronas para el análisis de la red de transporte público (Parras, 2015) y la difusión temporal de enfermedades (Ramírez, 2020), estimación de precipitaciones (Méndez y Calvo, 2015), análisis espacial del delito (Pezzuchi, 2003), desagregación de datos censales para el análisis urbano (Santos Preciado y García Lázaro, 2003), evaluación espacio-temporal de la sedimentación (Romero Méndez y Montes Galbán, 2009) y evaluación de la calidad del aire (Rodríguez, 2014).
Una temática en la que más interés han puesto los geógrafos es el cálculo de la densidad (Moreno Jiménez, 1991), que generalmente alude a la variable poblacional, y que puede ser definida como el cociente entre la cantidad de población que ocupa un área y la superficie de esta.
La modelización cartográfica de densidades puede abordarse desde dos perspectivas (Figura 2). Generalmente, cuando se trabaja con unidades espaciales discretas (puntos, líneas y áreas) se procede a la elaboración de cartografía temática de una variable o índice a partir de intervalos de clase, representados en colores graduados, que indican los valores de intensidad de la variable en cada unidad espacial. Cuando el objetivo es analizar la variación de los valores de una unidad discreta, se deben generar unidades espaciales continuas (celdas o píxeles), que presentan los valores estimados a partir de puntos (muestras) conocidos. Los métodos geoestadísticos de interpolación, que apuntan a la generalización de datos en superficies continuas, se denominan métodos de desagregación espacial. Tienen como objetivo generar una representación cartográfica compuesta por unidades espaciales de dimensiones menores a la unidad de referencia, superando las transiciones abruptas que se dan entre cada unidad discreta.
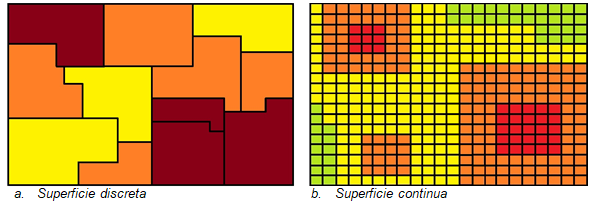
De esta manera, se presenta una alternativa metodológica para el estudio de la densidad en Geografía, que generalmente se ha basado en representarla a partir de unidades político-administrativas.
El método denominado Estimación de Densidad Kernel (Núcleo) fue desarrollado a mediados del siglo XX, y utilizado en el ámbito geográfico a partir de la década del 90, con una aceptación creciente por la comunidad de geógrafos cuantitativos (Moreno Jiménez, 1991; Brunsdon, 1995; Ercolano, 2002; De Cos Guerra, 2004; Buzai y Baxendale, 2012), actualmente favorecido por su automatización digital dentro de los principales softwares de SIG.
El Estimador de Densidad Kernel es un método no paramétrico. Es decir que la distribución de los datos no está sujeta a priori a un comportamiento que corresponda a determinados parámetros, como en el caso de una distribución normal (Silverman, 1986). Surge como método exploratorio más sofisticado y alternativo al histograma de frecuencias (Figura 3), a partir de generar una continuidad de un conjunto de datos, que da como resultado superficies de densidades relativas, a partir de un gradiente de valores continuos.
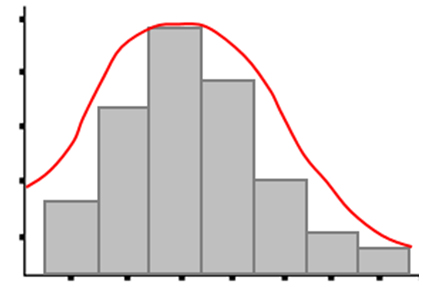
La función de densidad Kernel calcula la probabilidad de que un punto dado adquiera cierto valor de densidad a partir de un conjunto de datos de referencia. Es una función simétrica, a partir de la cual los valores de densidad van disminuyendo a la misma velocidad a medida que aumenta la distancia al punto central. De esta manera, se genera una distribución de densidad acumulada a partir de la suma de las funciones Kernel de cada punto de referencia. La fórmula de la función Kernel es la siguiente:
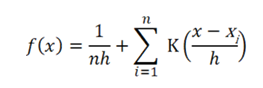
Donde es el punto que se quiere estimar; es el número de observaciones en la muestra; es el tipo de función Kernel; y es el ancho de banda o radio de estimación.
La función del tipo de Kernel va a definir la forma de las elevaciones, mientras que el ancho de banda determina el alcance o extensión de la función de cada Kernel individual. La suma de ellas genera como resultado la estimación de densidad acumulada (Figura 4).
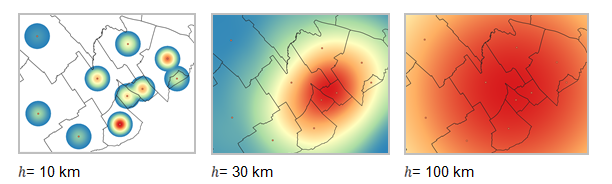
Existe una gran variedad de funciones Kernel, entre las cuales podemos mencionar los tipos Cuartico, Triangular, Uniforme, Triponderada, Epanechnikov, Gaussiano, Coseno y k2 de Silverman (Moreno Jiménez, 1991). Cada tipo de Kernel va a generar resultados distintos en la distribución de densidades; no obstante, según Moreno Jiménez (1991), más determinante que el tipo es el ancho de banda o amplitud del radio, el cual va a definir la varianza de la función de densidad (Figura 5). En este sentido, la elección de un ancho de banda pequeño tiende a concentrarse en los datos observados (puntos de referencia) en forma de picos de valores. Por el contrario, un ancho de banda de gran tamaño presenta una alta homogeneidad en las densidades, lo cual disminuye la variabilidad de la distribución continua. Si bien existen métodos para la determinación de los anchos de banda,4 se considera que el más óptimo es aquel que se ajusta a la densidad real.
En el siguiente apartado, vamos a desarrollar la aplicación metodológica en una temática de gran interés en el contexto actual de pandemia generada por el COVID-19, en el que la Geografía y su especialidad temática, la Geografía de la Salud, tienen mucho que aportar al análisis espacio-temporal de enfermedades (Olivera, 1993; Pickenhayn, 2008). En este sentido, el método de densidad Kernel se presenta con excelentes aptitudes como indicador de concentraciones espaciales de contagios.
Aplicación y resultados
Evolución de casos confirmados de COVID-19
El área de estudio cuenta, para el lunes 28 de diciembre de 2020, con un total de 108.720 casos confirmados acumulados, lo que representa un porcentaje del 18 % a nivel provincial. El primer caso positivo en la cuenca del río Luján se dio en el municipio de Luján, el día 11 de marzo, justamente el mismo día que fue declarada la pandemia por la Organización Mundial de la Salud. La situación actual en cuanto a casos confirmados se presenta con una fuerte amplitud, desde el valor más alto, con 19.530 casos, para el municipio de Moreno, al más bajo, 240 casos, registrado por el municipio de Suipacha. Entre estos valores extremos existe una amplia diferenciación en cuanto al impacto del COVID-19 en cada municipio. En la Figura 6, se puede observar un comportamiento logístico de la curva de crecimiento, con la definición de una serie de fases en la tendencia temporal del virus en el período de marzo a diciembre de 2020.
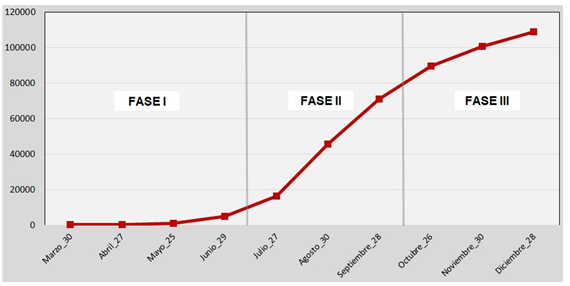
La primera fase (Fase I-Inicial) se desarrolla durante los meses de marzo a junio y presenta un crecimiento lento de casos positivos, con un promedio mensual de 890 nuevos contagios. En esta fase se registra un total acumulado de 4.760 casos positivos.
La segunda fase (Fase II-Expansiva) comprende los meses de julio a septiembre y se caracteriza por un crecimiento rápido de casos positivos, con una marcada tendencia exponencial y un promedio mensual de 8.379 contagios. En esta fase se registra un total de 70.856 casos positivos.
La tercera fase (Fase III-Decrecimiento) se produce entre los meses de octubre y diciembre, con una tendencia de desaceleración del crecimiento, a partir de la disminución de nuevos casos positivos, con un promedio mensual de 2.646 contagios. En esta fase se registra un total de 108.720 casos positivos.
Si bien la tendencia general, como hemos visto, indica una curva de crecimiento logístico, esta no se corresponde cuando se analiza el comportamiento temporal por municipio. En este sentido, se registran municipios que se encuentran en el transcurso y finalización de la Fase III, como Escobar, General Rodríguez, José C. Paz, Luján, Malvinas Argentinas, Moreno, Pilar, San Fernando y Tigre. Otros municipios están iniciando la Fase III, como Campana, Exaltación de la Cruz y Mercedes. Y, por último, aquellos municipios que están en el transcurso y finalizando la Fase II, como Carmen de Areco, Chacabuco, San Andrés de Giles y Suipacha.
Modelización cartográfica de densidades continuas
La aplicación metodológica pretende abordar uno de los posibles métodos para estimar densidades continuas. El método de estimación de densidades Kernel ha sido aplicado al análisis de la distribución espacio-temporal de la tasa de contagios de COVID-19, en los municipios de la cuenca del río Luján. Se utilizó el software QGIS (Versión 3.14) para el modelado cartográfico. Los parámetros del modelador requieren la precisión de la capa de entrada, el radio de influencia, el tamaño de la celda raster, una variable de peso o ponderación y el tipo de método Kernel. En la presente aplicación, hemos seleccionado un radio de 30 kilómetros y un tamaño de celda de 100 metros. Se asignó la variable Tasa de contagios (según meses) y se seleccionó el método Cuártico.5
El enfoque temporal, desde el análisis espacial cuantitativo (Buzai, 2010), pretende captar las variaciones de las distribuciones espaciales en el tiempo, en una perspectiva geográfica que recurre al pasado para descubrir el estado inicial de las distribuciones espaciales. Para explicar cómo sucedieron se aborda la combinación entre el espacio (dónde) y el tiempo (cuándo). A continuación, se presenta la distribución espacio-temporal de la densidad de la tasa de contagios (Figura 7) a partir de una secuencia cartográfica con datos mensuales acumulados, que corresponde a las fases de iniciación (abril y junio), de crecimiento acelerado (septiembre) y de decrecimiento (diciembre). El resultado cartográfico consiste en un mapa raster, que representa la variación espacial de la densidad de contagios asignando un color a cada intervalo de clase. El color define la intensidad de la variable, desde colores cálidos como un rojo fuerte, que indica valores muy altos, hasta colores fríos como el azul, que indica valores muy bajos.
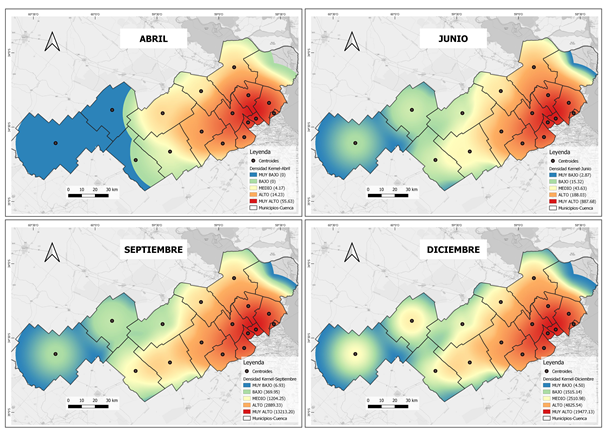
Los resultados cartográficos evidencian una marcada diferenciación espacial de la incidencia de los contagios en el interior de los municipios de la cuenca del río Luján, definiendo sectores de mayor dinamismo en la propagación espacio-temporal del virus. El patrón de distribución espacial presenta una forma radial o de anillos concéntricos, con una clara tendencia de disminución de los valores de densidad de contagios a medida que aumenta la distancia a los principales centros urbanos de cada municipio. Desde los primeros meses de pandemia, la difusión se inició desde ciudades de mayor tamaño poblacional, con un agrupamiento de unidades con las mayores densidades en el sector este, que corresponde a municipios pertenecientes al Área Metropolitana de Buenos Aires (AMBA) y que integran la mancha urbana del aglomerado Gran Buenos Aires, como Escobar, José C. Paz, Malvinas Argentinas, Moreno, Pilar, San Fernando y Tigre, que cuentan con una población en un rango que va de 200.000 a más de 500.000 habitantes, y que se consolidan como los mayores focos de contagios a medida que avanzan los meses. Por otro lado, tenemos los municipios con ciudades intermedias de importancia regional, cuya población ronda los 50.000 a 100.000 habitantes; tal es el caso de Campana, General Rodríguez, Luján y Mercedes. En ellos, si bien la población se concentra mayormente en la ciudad cabecera, existen localidades con una densidad poblacional media-baja; son características que inciden en el aumento de los casos positivos, aunque con un impacto menor. La tendencia espacio-temporal indica una disminución hacia el sector oeste, donde se encuentra una baja incidencia en la mayoría de los municipios, que cuentan con bajos niveles de aglomeración urbano-poblacional y alta dispersión de asentamientos urbanos, y cuya organización espacial presenta una fuerte vinculación al ámbito rural. Estos municipios presentan la menor densidad de contagios, con una fuerte concentración en la ciudad cabecera, ya que las localidades menores cuentan con niveles de población muy bajos. Tal es el caso del municipio de San Andrés de Giles, cuya ciudad cabecera cuenta con alrededor de 23.000 habitantes y está integrado por seis localidades en un rango de 100 a 1.000 habitantes, lo cual favorece una propagación lenta del virus. No obstante, en los últimos meses han presentado un aumento significativo de casos positivos, que los han llevado a ocupar las categorías media-alta para diciembre, con valores en la tasa de contagios que se encuentran entre 2.000 a 3.000 casos, como en Carmen de Areco, Chacabuco, San A. de Giles y Suipacha.
Consideraciones finales
La Geografía Cuantitativa, como ciencia espacial, y la metodología del análisis espacial cuantitativo basada en el uso de SIG y técnicas geoestadísticas han logrado realizar interesantes aportes al análisis y modelización espacio-temporal del comportamiento del COVID-19. En el presente trabajo, nos hemos centrado en la aplicación metodológica del Estimador de Densidad Kernel como método de interpolación espacial orientado a la modelización cartográfica de la densidad de contagios de COVID-19 en los municipios de la cuenca del río Luján.
Los resultados obtenidos indican una fuerte tendencia de concentración espacial de contagios en las áreas urbanas de mayor densidad poblacional, correspondientes a las ciudades cabecera de los municipios que forman parte del Aglomerado Gran Buenos Aires, que van disminuyendo a medida que aumenta la distancia a estos centros urbanos. De esta manera, se presenta una configuración espacial diferenciada a partir de la posición relativa de cada centro urbano como principal difusor de los contagios, que condiciona la propagación del virus a las localidades menores que se encuentran en el interior de cada municipio. En este sentido, el análisis espacial realizado pretende generar una herramienta de base espacial para distintas posibilidades de aplicación en el ámbito del ordenamiento territorial.
Referencias
Bosque Sendra, J.; García, R. (2001). Métodos de interpolación para la elaboración de un modelo digital de elevaciones. Estudios geográficos, 245. pp. 605-620.
Buzai, G. D. y Baxendale, C. (2011). Análisis socioespacial con Sistemas de Información Geográfica. Tomo 1. Perspectiva científica/Temáticas de base raster. Buenos Aires: Lugar Editorial.
Buzai, G. D. y Baxendale, C. (2012). Análisis socioespacial con Sistemas de Información Geográfica. Tomo 2. Ordenamiento territorial/Temáticas de base vectorial. Buenos Aires: Lugar Editorial.
Buzai, G. D., Baxendale, C., Humacata, L. y Principi, N. (2016). Sistemas de Información Geográfica. Cartografía temática y análisis espacial. Buenos Aires: Lugar Editorial.
Brunsdon, Ch. (1995). Estimating probability furces for geographical point data: and adaptive kernel algorithm. Computers and geosciences. 21(7). pp 874-894.
De Cos Guerra, O. (2004). Valoración del método de densidades focales (Kernel) para la identificación de los patrones espaciales de crecimiento de la población en España. GeoFocus (Artículos), 4. 136-165.
Ercolano, S. (2002). Densidad de población y sustentabilidad en la ciudad de Zaragoza. En L. A. Longares Alardeen y J. L. y Peña Monné (Eds.), Aportaciones geográficas en memoria del profesor L. Miguel Yetano Ruiz. Zaragoza: Universidad de Zaragoza, Departamento de Geografía y Ordenación del Territorio, pp. 173-182.
Humacata, L. (2020). Análisis espacial del COVID-19 en los partidos de la cuenca del río Luján (Provincia de Buenos Aires, Argentina), durante los meses de marzo a agosto de 2020. Revista Cardinalis, 8(15), 121–136. Recuperado de https://revistas.unc.edu.ar/index.php/cardi/article/view/31763/32727
Instituto Nacional de Estadística y Censos, INDEC (2013). Censo Nacional de Población, Hogares y Vivienda 2010. Base de datos REDATAM. Instituto Nacional de Estadística y Censos de la República Argentina. Buenos Aires, Argentina. Recuperado de https://www.indec.gob.ar/
Méndez, M. y Calvo, L. A. (2015). Evaluación de diversos modelos de interpolación espacial para la estimación de la precipitación promedio en la cuenca alta de río Toro. PROHIMET. Costa Rica.
Ministerio de Salud de la República Argentina (2020). Reporte Diario COVID-19. Recuperado de https://www.argentina.gob.ar/Coronavirus/informe-diario
Moreno Jiménez, A. (1991). Modelización cartográfica de densidades mediante estimadores Kernel. Treballs de la Societat Catalana de Geografia, 30, 155-170.
Olivera, A. (1993). Geografía de la Salud. Madrid: Síntesis.
Parras, A. (2015). Modelización de la red de transporte público a partir de isócronas. En G. D. Buzai, G. Cacace, L. Humacata y S. Lanzelotti, Teoría y métodos de la Geografía Cuantitativa. Libro 1. Por una Geografía de lo real. Mercedes: MCA Libros. pp 195-21
Pezzuchi, G. (2003). Análisis espacial del delito. Análisis exploratorio de enfrentamientos policiales, años 1999-2001 en el Conurbano Bonaerense-Argentina (Tesis de Maestría en Sistemas de Información Geográfica). Quito: Universidad San Francisco de Quito.
Pickenhayn, J. A. (2008). Geografía de la Salud: el camino de las aulas. En Ch. Barcellos (Org.). A Geografía e o contexto dos problemas de saúde (pp. 63-84). Río de Janeiro: Abrasco.
Pumain, D. y Saint Julien, T. (2014). Análisis espacial. Las interacciones. Santiago: Pontificia Universidad Católica de Chile. Serie GEOlibros, n° 21.
Ramírez, L. (2020). Evolución, distribución y difusión del COVID-19 en Argentina: primer mes (03/03/2020 - 02/04/2020). Revista Posición. Dossier: análisis geográfico del COVID-19. Instituto de Investigaciones Geográficas, Universidad Nacional de Luján, 3.
Romero Méndez, A. y Montes Galbán, E. (2009). Evaluación espacio–temporal de la sedimentación en el embalse Burro Negro, estado Zulia/Venezuela mediante el uso combinado de SIG–Ecosonda–DGPS. GeoFocus (Artículos), 9, 209-231.
Santos Preciado, J. M. y García Lázaro, F. J. (2003). El método dasimétrico-picnofiláctico: un procedimiento para la desagregación de datos censales. IX Conferencia Iberoamericana de SIG. Universidad de Extremadura. CD-ROM, 1-16.
Silverman, B. W. (1986). Density Estimation for Statistics and Data Analysis. Londres: Chapman & Hall.
Unwin, D.J. (1996). GIS, spatial analysis and spatial statistics. Progress in Human Geography. 20(4), 540-551.
Warntz, W. (1975). La nueva geografía como teoría de sistemas espaciales: ¿cuenta mucho la vieja “física social”?. En R. J. Chorley (Ed.), Nuevas tendencias en geografía (pp. 137-187). Madrid: IEAL.
Notas

